扩展有限元中边界条件的施加

冷 飞 张 然

(河海大学 土木与交通学院， 南京 210098)



扩展有限元中边界条件的施加

冷 飞 张 然

(河海大学 土木与交通学院， 南京 210098)

扩展有限元施加边界条件的方法与有限元不同，但尚无文献进行详细的说明．本文由有限元的控制方程和边界条件的基本格式出发，说明了扩展有限元施加应力和位移边界的原理，以单个带裂缝单元为例给出了Standard-XFEM和Shifted-XFEM模式下扩展有限元施加边界条件的具体实现过程．最终，通过一个受均布荷载的简支梁验证了本文介绍方法的正确性．结果表明：对于应力边界，应由最小位能原理导出的公式计算等效结点荷载，不同位移模式下，由外部荷载计算等效结点荷载的公式相同，但得到的结点荷载向量不同．位移边界则应将不同的位移模式在约束处所满足的方程带入控制方程求解．虽然均采用上述原理施加边界条件，但采用不同位移模式时，实现边界条件的具体方法不尽相同．

扩展有限单元法； 位移边界条件； 应力边界条件； 非线性计算

0 引 言

扩展有限单元法最初应用于预设有裂缝、孔洞、夹杂的线弹性材料的计算，属于线性计算范畴，随着理论研究的发展，在非线性材料与结构的计算中也有越来越多的应用[1-2]．对于非线性计算，增量法是一种非常常见的迭代计算方法．这种方法要求在每一步迭代中均计算不平衡力，并将其作为结点荷载继续计算．因此，在非线性计算中会遇到给带裂缝单元施加荷载的问题．当加载区域存在不连续问题时，即使是线性计算也会遇到上述问题．此外，对于线性以及非线性材料的实际结构，裂缝有可能会出现在约束附近，因而如何给带裂缝单元施加约束条件也是实际结构扩展有限元分析会遇到的问题之一[3-4]．

在有限元计算中，无论是施加荷载还是施加约束，均属于控制方程的边界问题，即，对于计算域Ω，控制方程为

(1)

在其边界Γ上，应满足

(2)

在扩展有限元中，也应按以上边界条件处理带裂缝单元的位移边界或应力边界[5]．在实际计算中，对于位移边界，应根据不同的位移模式，对边界处位移采取拉格朗日乘子法[6-8]或罚函数法[9-10]等具体方法进行处理；对于应力边界，可利用最小位能原理得到等效结点荷载的计算公式．

以上方法与常规有限元处理位移与应力边界条件的方法完全相同，但实际结果却不完全相同．由于没有文献或资料专门对此问题进行详细解释，部分研究者在涉及此类问题时按常规有限元直接规定或假设应如何施加边界条件，如文献[11]则规定外荷载只作用在常规自由度却并未说明原因，部分研究人员认为某结点受到约束时该点常规自由度与富集自由度的位移均应为0等．因而，需要对扩展有限元如果施加边界条件进行明确的说明．

本文将严格由边界条件方程出发，给出扩展有限元中standard XFEM模式与Shifted-XFEM模式施加位移边界条件和应力边界条件的具体方法，并通过相应的算例验证其正确性．

1 Standard XFEM模式下边界条件的施加

1.1 Standard XFEM模式下的位移边界条件

Standard XFEM的位移模式为

(3)

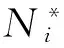
(4)

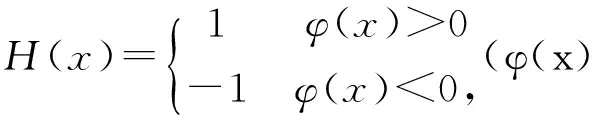
在某一点施加位移约束时，应由式(4)计算得到该点满足式(2)的边界条件，并将其作为控制方程的约束条件．一般而言，该约束条件为关于u和a的表达式．

图1为带裂缝的富集单元，边长为2l，竖直方向裂缝经过单元形心．结点1、结点2和结点3分别受到x向、双向和y向约束．u1～u8分别表示各结点x方向和y方向的常规自由度，a1～a8分别表示1到4节各结点x方向和y方向的富集自由度．因此，单元的位移向量可写为

(5)

图1 开裂单元受结点集中荷载

对于结点1，由式(3)，其x向位移为u1+a1，因其受到支座的约束作用，应有u1+a1=0，这就是控制方程应满足的位移边界条件．同理也可得到其他结点的位移边界条件．若采用拉格朗日乘子法处理该边界条件，控制方程还应满足以下条件：

(6)

其中λ1，λ2，λ3和λ4为拉格朗日乘子．将上述4个位移边界条件的表达式引入整体刚度矩阵K中后即可得到施加位移边界条件后的新整体刚度矩阵K*．受版面所限，本文只列出将式(6)中第一个子式引入整体刚度矩阵后的新K*，即

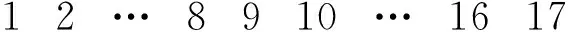
如此，就可以求出单元的位移向量u．

由该例可看出，对于标准模式的扩展有限元，虽然其控制方程与有限元相同，但当带裂缝单元受到位移约束时，不能像有限元一样简单认为被约束结点的常规自由度与富集自由位移均为0，而应由位移插值模式得出对应自由度u和a的关系，再耦合进刚度矩阵．

1.2 Standard XFEM模式下的应力边界条件

按照最小位能原理[12]，易知扩展有限元常规自由度上的结点荷载与有限元完全相同，富集自由度所对应的结点荷载为

(7)

其中，b为体力，t为面力，F为集中力．

由上式可见，富集自由度结点荷载的计算方法与常规有限元是一致的．仍以图1所示单元为例，在其1、4结点施加竖直向上的集中荷载，集中荷载大小为F．由有限元中结点荷载的计算方法及式(7)，可得该单元的等效节点荷载向量为

(8)

现假设泊松比μ=0，根据式(6)施加约束条件，由式(8)所示荷载向量可计算得到该单元内的应力分布σ为

(9)

如果用有限元法计算图1所示单元，当采用片状裂缝模型时和分离裂缝模型时，计算得到的应力分别为

(10)

(11)

观察式(9)至式(11)所示的应力分布可发现：采用片状裂缝模型时，该单元在荷载方向为轴拉构件，因而单元应力呈均匀分布，且只在荷载方向存在正应力；采用分离模型时，裂缝两侧分别为两个角点受力的矩形单元，类似两个偏拉构件，因而两个单元内不仅在荷载方向有正应力，还有剪应力存在，正应力在单元的左右两侧最大，中间为零，剪应力在单元的上下两侧最大，中间为零；采用扩展有限元方法计算时，所得到的应力结果与分离式裂缝模型的结果相同，从而可认为本文说明的施加荷载的方法是正确的．考虑到采用分离裂缝模型计算过程中重新剖分网格的工作量及难度，扩展有限元在分析裂缝问题时具有明显的优点．

对于更为一般的情况，讨论集中荷载不作用于结点时的等效结点荷载．以图2所示单元为例，在单元上边缘±l/2处施加大小为F、方向向上的集中荷载．该情况下，无论单元视为一个整体，还是将裂缝两侧视为独立的两部分，单元均应为单轴受拉受力状态．

由式(7)可计算得到图2单元的等效结点荷载为

(12)

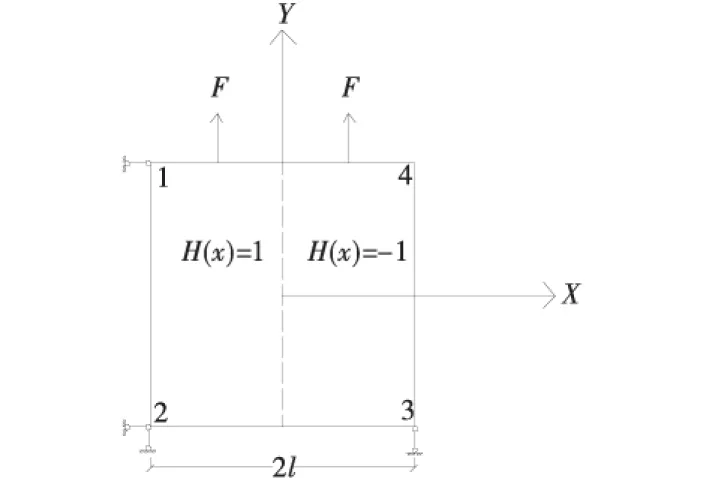
图2 开裂单元受非结点集中荷载

这与单向轴拉应力状态(即式(10))的等效结点荷载完全一致，因而可再次验证本文施加结点荷载方法的正确性．对不在节点上的集中荷载进行积分即可得到面荷载或体荷载的等效结点荷载，受于篇幅的限制，本文不再进行累述．

2 Shifted-XFEM模式下边界条件的施加

2.1 Shifted-XFEM模式下的位移边界条件

加强函数同样选为Heaviside函数时，Shifted-XFEM的位移模式为

(13)

其中，H(xi)为节点处的Heaviside函数在i结点处的数值．

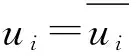
2.2 Shifted-XFEM模式下的应力边界条件

根据最小位能原理，富集自由度上所对应的荷载为

(14)

仍采用图2所示单元进行说明．根据式(14)计算不难发现，富集自由度上对应的等效结点荷载均为0，因此，等效结点荷载向量可以表示为

(15)

同样假设该单元的泊松比μ=0．根据2.1节方法施加位移边界，由式(15)确定的结点荷载可求出节点位移向量，计算得到该单元内的应力分布σ与式(9)所示结果相同，即可得到正确的应力解答．

对图2所示的集中力不作用于单元结点的一般情况，由式(14)可以得到单元的等效结点荷载为

(16)

式(16)所给出的结点荷载与式(10)所示单轴受拉应力状态在Shifted-XFEM模式下的结点力相互平衡．

限于篇幅，本文不再讨论由集中力等效结点荷载积分得到分布力等效结点荷载的过程．

3 算例验证

本文采用的算例与文献[13]中所计算的受均布荷载的简支梁算例相同．采用自编的钢筋混凝土扩展有限元程序HohaiRCFE-P进行计算，将计算结果与规范结果进行比较．

如图3所示简支梁，截面尺寸为250mm×600mm，长度为7.2m，承受标准值为10.0kN/m的均布荷载．采用C25混凝土，配有两根直径为18mm的HRB335纵向受拉钢筋，混凝土保护层厚度为35mm．采用增量法进行计算，分20个荷载步施加，每一荷载步的增量为0.5kN/m，每一步迭代中将不平衡力视为结点荷载按本文方法进行施加．共划分876个混凝土单元，单元尺寸为100mm×50mm；钢筋采用2结点杆单元(共73个)，网格剖分如图3所示．粘结滑移关系采用Houde-双折线形式．

图3 受均布荷载的简支梁

表1列出了计算得到的裂缝宽度，并与《混凝土结构设计规范》(GB50010-2010)裂缝宽度公式计算结果进行了对比．需要说明的是，规范裂缝宽度公式考虑了长期效应(扩大系数为1.5)，而本文扩展有限元计算中没有考虑荷载长期作用的影响，因而表1中按规范计算的裂缝宽度除以了1.5的扩大系数．

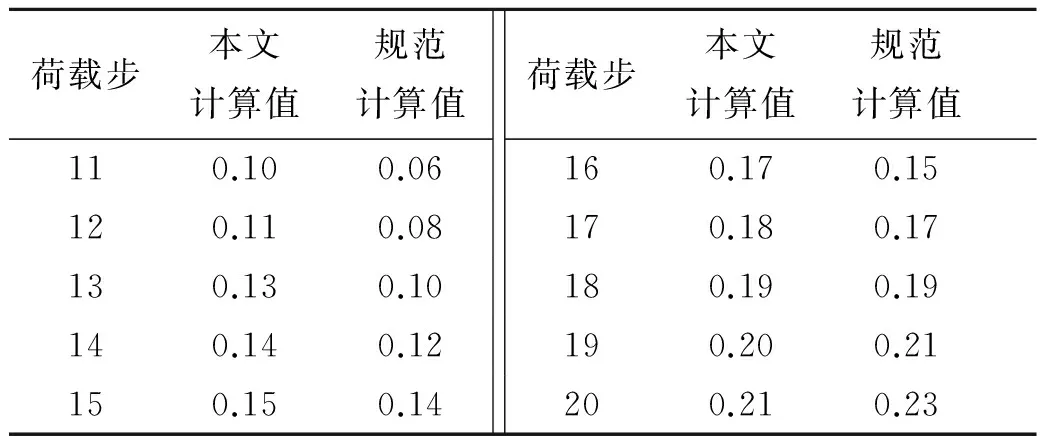
表1 最大裂缝宽度计算值比较 (单位：mm)

从表1可以看出，裂缝宽度较小时，与规范公式计算结果相比，本文方法计算得到的裂缝宽度误差稍大，但当裂缝宽度接近各类环境下的裂缝宽度限值时，本文结果与与规范裂缝宽度计算值吻合良好，从而验证了本文所述方法的正确性．

4 结 论

本文由有限元的控制方程和边界条件的基本格式出发，说明了扩展有限元施加应力和位移边界的方法，以单个带裂缝单元为例给出了Standard-XFEM和Shifted-XFEM模式下扩展有限元施加边界条件的具体实现过程．最终，通过一个受均布荷载的简支梁验证了本文介绍方法的正确性．由本文的工作，可以得到以下结论：

1)扩展有限元施加边界条件的原理与有限元相同，对位移边界，结点实际位移应与约束条件协调；对应力边界，可由最小位能原理确定等效结点荷载．

2)位移边界条件的具体实现方法因位移模式的不同而不同．Standard-XFEM模式下，应将位移边界条件所满足的方程带入基本方程求解；Shifted-XFEM模式下位移边界条件对富集自由度的广义位移没有约束作用．

3)不同位移模式下，由外部荷载计算等效结点荷载的公式相同，但得到的结点荷载向量不同．

4)扩展有限元中，集中荷载是否作用在结点上产生不同的等效结点荷载，其应力计算结果与采用分离式单元模型的有限元计算结果相同．除Standard-XFEM和Shifted-XFEM模式外，扩展有限元还有其他常用位移模式．不同位移模式下，施加边界条件的原理都是相同的，限于篇幅，本文不再重复．

[1] Theiner Y, Hofstetter G． Numerical Prediction of Crack Propagation and Crack Widths in Concrete Structures[J]．Steel Construction, 2009, 31(8)：1832-1840．

[2] 方修君, 金 峰, 王进廷．用扩展有限元方法模拟混凝土的复合型开裂过程[J]．工程力学, 2007, 24(S1)：46-52．

[3] Mo⊇s N, Béchet E, Tourbier M． Imposing Essential Boundary Conditions in the Extended Finite Element Method[J]． International Journal for Numerical Methods in Engineering, 2006, 67(12)：1641-1669．

[4] 余天堂．摩擦接触裂纹问题的扩展有限元法[J]．工程力学, 2010(4)：84-89．

[5] 余天堂．扩展有限单元法 - 理论、应用及程序[M]．南京：科学出版社, 2014．

[6] Éric Béchet, N Mo⊇s, B Wohlmuth． A Stable Lagrange Multiplier Space for Stiff Interface Conditions within the Extended Finite Element Method[J]． International Journal for Numerical Methods in Engineering, 2008, 78(8)：931-954．

[7] Dolbow J, Mo⊇s N, Belytschko T． An Extended Finite Element Method for Modeling Crack Growth with Frictional Contact[J]． Computer Methods in Applied Mechanics & Engineering, 2001, 190(s51-52)：6825-6846．

[8] Haziza F． The Extended Finite Element Method and Its Implementation in 2D in the Aster Code[D]．Stockholm：Royal Institute of Technology, 2006．

[9] Liu F, Borja R I． A Contact Algorithm for Frictional Crack Propagation with the Extended Finite Element Method[J]． International Journal for Numerical Methods in Engineering, 2008, 76(10)：1489-1512．

[10] Kim T Y, Dolbow J, Laursen T． A Mortared Finite Element Method for Frictional Contact on Arbitrary Interfaces[J]． Computational Mechanics, 2007, 39(3)：223-235．

[11] 方修君, 金 峰, 王进廷．基于扩展有限元法的粘聚裂纹模型[J]．清华大学学报(自然科学版), 2007, 47(3)：344-347．

[12] 王勖成．有限单元法[M]．北京：清华大学出版社, 2002．

[13] 李 俊．基于钢筋混凝土扩展有限元的钢筋应力求解方法研究[D]．南京：河海大学, 2015．

[责任编辑 周文凯]

Implementation of Boundary Conditions in Extended Finite Element Method

Leng Fei Zhang Ran

(College of Civil & Transportation Engineering, Hohai Univ., Nanjing 210098, China)

It is different to implement boundary conditions in extended finite element method(XFEM) and finite element method(FEM). But there is no detailed statement in any

so far. Starting with the basic format of control equations and boundary conditions in FEM, the paper introduces how to impose the force boundary conditions and displacement boundary conditions in XFEM. The detailed processes of the implementation of boundary conditions under Standard-XFEM and Shifted-XFEM are given by an example of a single cracked element. Finally, the method in the paper is validated by an example of a simply supported beam under uniform load. The results show that, for the stress boundary conditions, equivalent nodal loads should be calculated by the formula derived from the principle of minimum potential energy, under different displacement modes; although, the formula of equivalent nodal load has no different; the nodal load vectors are different. For the displacement boundary conditions, the different equations satisfying with constraint condition for different displacement mode should be introduced into the control equation. Although the above basic method is the same, how to implement it is different for different displacement mode.

extended finite element method; displacement boundary condition; force boundary condition; nonlinear calculation

10.13393/j.cnki.issn.1672-948X.2016.05.011

2016-03-23

国家自然科学基金(51179063)

张 然(1993-)，男， 硕士研究生，研究方向为混凝土结构数值计算．E-mail：popeyecross@outlook.com

TU31

A

1672-948X(2016)05-0059-05