HBV模型在汤旺河流域的应用研究

李海川 郝振纯 尼玛旦增 赵思远 孙爱立

(1. 河海大学 水文水资源与水利工程科学国家重点实验室， 南京 210098； 2. 西藏自治区水文水资源勘测局山南分局，西藏 山南 856000； 3. 宁波市水利水电规划设计研究院，浙江 宁波 315192)



HBV模型在汤旺河流域的应用研究

李海川1郝振纯1尼玛旦增2赵思远3孙爱立1

(1. 河海大学 水文水资源与水利工程科学国家重点实验室， 南京 210098； 2. 西藏自治区水文水资源勘测局山南分局，西藏 山南 856000； 3. 宁波市水利水电规划设计研究院，浙江 宁波 315192)

通过对汤旺河流域构建HBV模型进行日径流模拟研究，来评估HBV模型在我国东北地区的适用性．在对参数进行敏感性分析的基础上进行模型参数率定和验证，并以流域出口晨明站为例，选择多种假定的情景，分析降水和气温的变化对于径流的影响．结果表明，HBV模型中响应模块(K0、K1、K2、UZL)和汇流模块(MAXBAS)的几个参数最为敏感，土壤模块参数(BETA、LP)较敏感；模型在汤旺河流域模拟效果理想，4个站点控制流域的Nash-Sutcliffe效率系数Reff和确定性系数R2均达0.77以上，能较好地模拟洪水对降雨的响应过程，表明模型在东北地区具有较好的适用性，且降水的变化较气温对汤旺河流域的水文循环影响更大．

汤旺河流域； HBV模型； 参数敏感性； 水文响应

气候变化下的水循环演变规律是当今国际水科学研究的热点问题，寒区是反映气候变化的敏感地带，同时也是我国重要的水资源发源地，而对于寒区水文的认识尚存在很多疑问．水文模型是研究水文自然规律和解决水文实践问题的重要工具．所以，寒区水文模型的研究对于认识寒区水循环机理、水量平衡和水文过程具有重要意义．

HBV模型是瑞典国家水文局(SMHI)针对北欧寒区流域特点开发研制的水文预报模型．相对于其他模型，HBV模型有很多独特的优点，一方面，它能够适应于各种复杂气候条件下的水文模拟；另一方面，模型还具有输入参数少、适合大流域、模拟精度高等优点．近年来，HBV在国内也逐渐得到了广泛应用，赵彦增等[1]利用HBV水文模型对淮河官寨流域进行了模拟研究；靳晓莉等[2]利用该模型通过参数区域化有效地应用到东江流域无资料地区的模拟研究；高红凯等[3]采用HBV模型对冬克玛底河流域年月尺度径流深进行模拟研究，并得出该地区径流深的增加主要是温度升高所致；王有恒等[4]选择在白龙江流域构建HBV模型，较好模拟出了洪水对降水的响应过程．

本文以小兴安岭地区汤旺河流域为研究区域，应用HBV light模型进行模拟研究，并对参数敏感性进行了分析研究，以期为今后进一步研究气候对汤旺河流域水资源的影响提供理论基础．

1 研究区概况

汤旺河流域位于黑龙江省的东北部，属于小兴安岭腹地，是典型的山溪型森林流域．流域平均海拔500 m，地势北高南低，地形较为复杂，上游山势缓和，河谷宽广，多山间盆地，沿河沼泽发育，地貌类型为低山、丘陵、谷底，是我国的主要林区之一[5]．汤旺河是松花江下游的一条主要支流，河道全长为506 km，流域面积达20 838 km2，多年平均径流量55.2亿m3．

汤旺河流域地处亚寒带大陆性季风气候区，春、秋两季时间较短，春季降雨较少、风比较大且气温回升较快；夏季多雨且潮湿；秋季温度较低，霜冻时间早；冬季寒冷而漫长，降雪天数多．多年平均气温约为1℃，年降雨量约为610 mm，年内降水集中在6～9月，河流补给以融雪、降雨补给为主．全年日照时数2 280～2 550 h，无霜期100～120 d．流域林地面积大，对地面气温和湿度有一定的调节作用，蒸发量较小，且受季节影响明显，多年平均蒸发量为510 mm．

2 模型建立和分析方法

2.1 基础数据

当前流域内主要设置有5个水文站，其中五营站、晨明站2个站设置在汤旺河干流上，伊春站位于支流伊春河河口，南岔站和带岭站位于支流南岔河河道，如图1所示．本文所用模型驱动数据均来自中国气象科学数据共享服务网和水文年鉴，包括五营、伊春、南岔和晨明4个水文站以及各水文站控制流域内雨量站的2005～2012年逐日降水、流量资料和伊春气象站2005～2012年逐日气象资料．其中，模型需要的各水文站点控制断面以上面降雨量数据是运用泰森多边形法分别得出，潜在蒸散发数据由以上气象资料采用Penman-Monteith公式计算得到，各站点的基本情况见表1．

图1 汤旺河流域内观测站点分布图

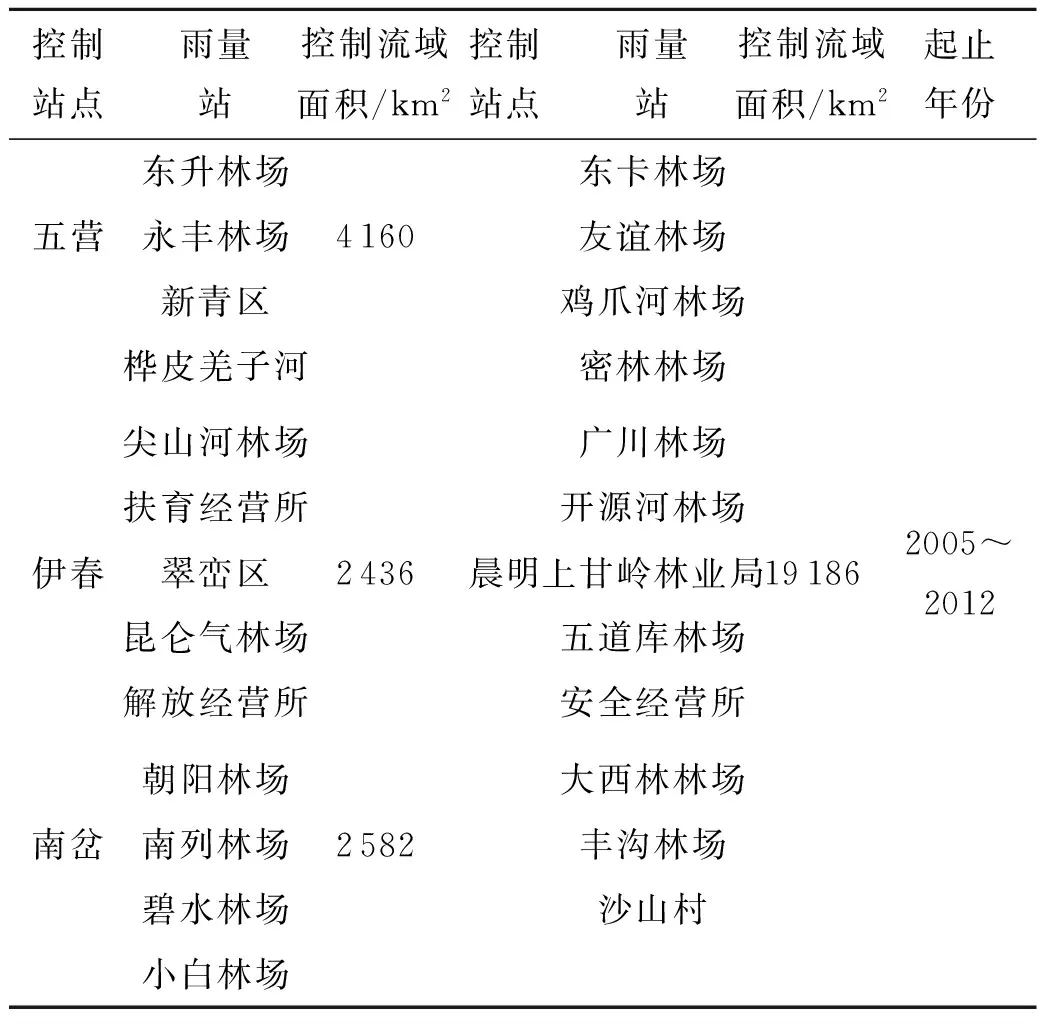
控制站点雨量站控制流域面积/km2控制站点雨量站控制流域面积/km2起止年份东升林场东卡林场五营永丰林场4160友谊林场新青区鸡爪河林场桦皮羌子河密林林场尖山河林场广川林场扶育经营所开源河林场伊春翠峦区2436晨明上甘岭林业局191862005～2012昆仑气林场五道库林场解放经营所安全经营所朝阳林场大西林林场南岔南列林场2582丰沟林场碧水林场沙山村小白林场

2.2 模型概述

HBV模型是一种半分布式、概念性降雨径流模型，由于该模型的结构层次比较清晰，输入资料简单，参数物理意义明确，并且综合考虑了降水、气温、产流、土壤、汇流等因素对流域内水文过程的影响，在过去的30多年里被广泛应用于洪水设计、水文预报、气候变化影响研究、水量平衡研究和地下水模拟等诸多方面．该模型主要以日降水、日均温、日潜在蒸散发作为输入数据，输出量为日径流深，共分为4个模块：融雪模块、土壤模块、响应模块和汇流模块[6]．其中，融雪模块是HBV模型针对寒区流域开发的一个重要模块：

首先模型根据子流域的日均温判断降水方式．当日均温T(℃)大于临界温度值TT(℃)时，降水以降雨的形式进入HBV模型中；当日均温T小于临界温度值TT时，降水则以降雪的形式进入模型中，此时需要乘以一个降雪校正系数SFCF(-)来计算累积雪量．

HBV模型采用度日因子(degree-day factor)模型计算冰雪消融；此外，随着温度的降低，在融水下渗的过程中会再次发生冻结，所以模型还考虑了融水再冻结过程，消融量Melt(mm·d-1)与冻结的水量Refreezing(mm·d-1)分别由式(1)和(2)表示：

(1)

(2)

式中，CFMAX(mm·d-1·℃-1)为融雪因子；CFR(-)为再冻结系数．

2.3 参数敏感性分析方法

现代水文模拟一般认为导致模型模拟结果好与差的不是模型单个参数，而是参数组合．本文所用参数敏感性分析方法需要首先设定模型参数的分布取值范围，利用Monte-Carlo随机采样方法获取参数值组合，放入模型中进行模拟．选定似然目标函数，计算模型模拟结果与观测值之间的似然函数值，通过判断各参数对模型模拟结果不确定性的影响(即绘制参数与似然值散点分布图)来分析模型参数的敏感性．

2.4 模型评价标准

模型参数通过Monte-Carlo方法来率定．采用确定性系数R2和Nash-Sutcliffe效率系数Reff两个指标来度量模拟效果，两个系数反映了观测径流值和模拟径流之间的吻合度，R2用来度量均值的模拟效果，Reff用来度量极值的模拟效果[7]，计算公式见(3)、(4)．

(3)

(4)

3 结果分析

3.1 参数敏感性分析

对参数进行敏感性分析是为了判断哪些参数的改变对模型的结果影响更大，从而提高模型校准效率．根据4个水文站点控制流域实际下垫面情况，分别针对各控制流域参数取值区间，见表2，采用Monte-Carlo方法将随机采样得到的10万组参数代入HBV模型，参数先验分布服从均匀分布，分别得到10万个模拟流量过程和特征值．从这10万个模拟流量过程和特征值中发现，模拟流量过程线的整体趋势是相同的，其中有些和观测流量过程线拟合得很好，有些则或高或低地偏离观测值，充分体现出水文模型的不确定性[8-9]．同时，不同参数组合可以得到十分相似的模拟似然值，即所谓的“异参同效”现象，很好地印证了GLUE方法的中心观点：导致模型模拟结果好与坏的关键并不是单个参数，而在于模型的参数组合[10]．由此可见，由人工率定而来的“最优”参数组是不可靠的，具有高不确定性[11]．

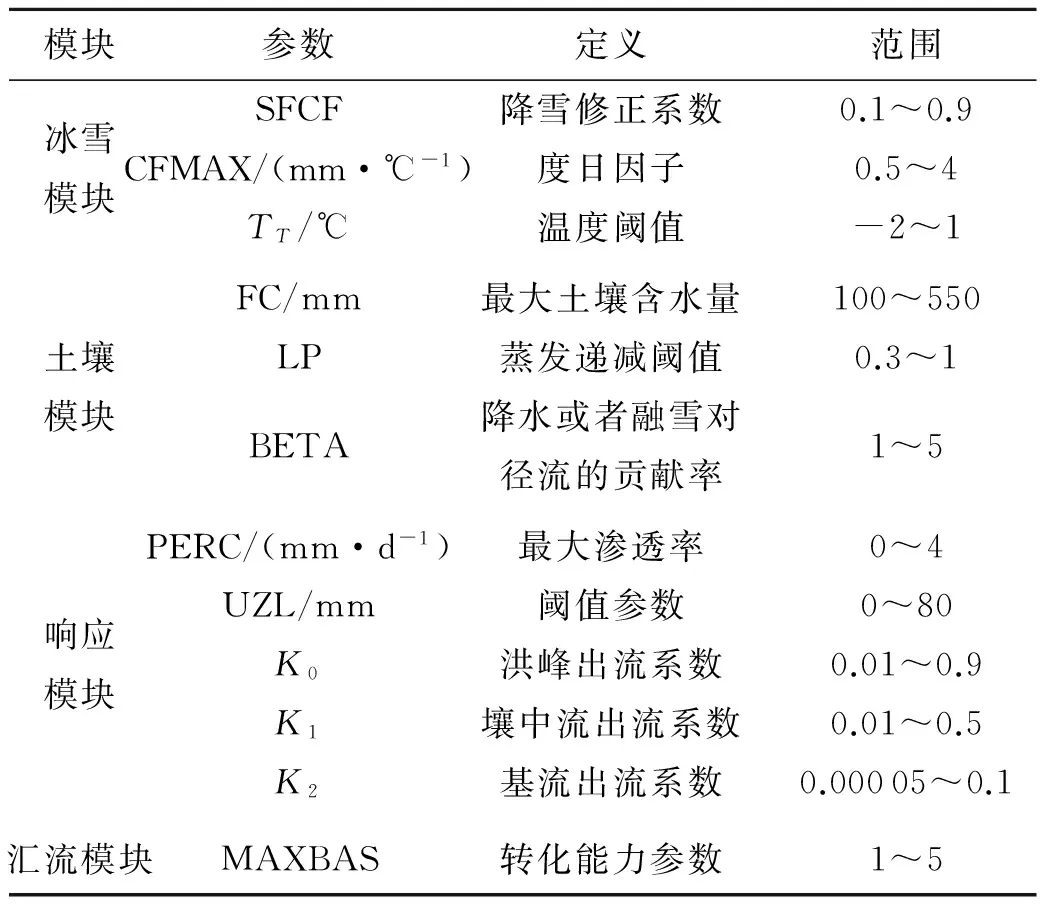
表2 HBV模型参数取值范围

利用HBV模型对4个站的控制流域径流进行模拟．以确定性系数作为似然目标函数，得到各参数与似然值散点分布图，可以判断出各站点模型参数的敏感性较为一致，下面以南岔站模型参数与似然值散点分布图为例，据此可将参数归纳为以下3类：

1)不敏感参数．SFCF、TT、CFMAX、FC、PERC这5个参数的似然值散点分布图分布均匀，无明显的变化趋势，对确定性系数影响很小，属于不敏感参数．如图2所示．

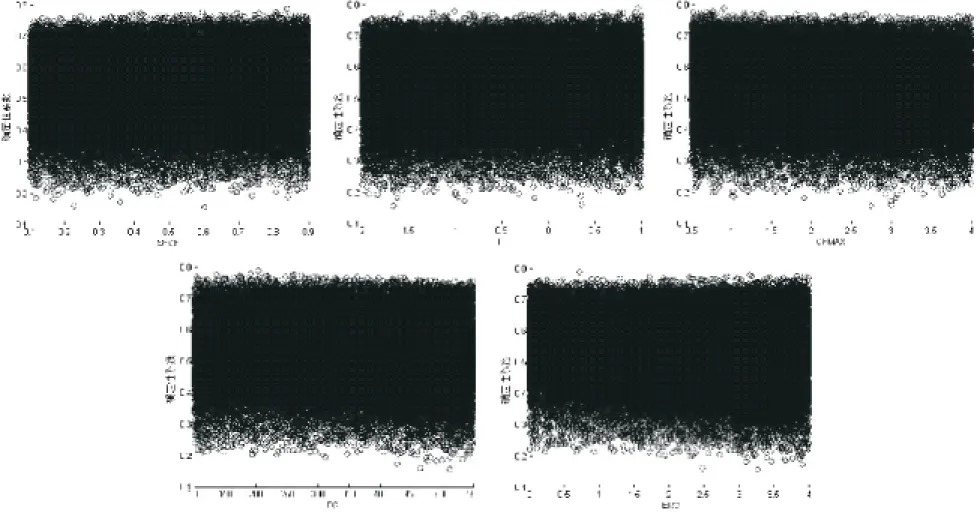
图2 不敏感参数似然值散点分布图

2)敏感参数．K0、K1、K2、UZL、MAXBAS，这5个参数的似然值散点分布图有明显的高值区，说明这4个参数对HBV模型确定性系数的影响较大，为敏感参数．K0、K1、K2、UZL均为响应模块参数，MAXBAS为汇流模块参数，表明响应模块和汇流模块的参数对模型结果的影响较大．如图3所示．

图3 敏感参数似然值散点分布图

3)较敏感参数．BETA、LP，这两个参数的似然值散点分布图与不敏感参数相比有较为明显的起伏变化趋势，但相对于敏感参数对模型模拟结果的影响而言，它对模型输出的确定性系数影响稍小，BETA、LP均为土壤模块参数，属于较敏感参数．如图4所示．

图4 较敏感参数似然值散点分布图

3.2 模拟结果

利用HBV模型对汤旺河流域内4个水文站点控制流域的径流过程进行模拟，各站具体模拟结果见表3．

表3 4个水文站径流模拟结果统计

汤旺河流域日径流模拟和日降雨过程如图5～8所示．由图知，降雨量和径流年际变化趋势一致，例如五营站2005～2006年降雨量较大，对应的径流深也较大；2007～2009年降雨量较小，相应的径流量也较小．因此可见HBV模型能较好地模拟洪水对降雨的响应过程．

图5 五营站率定期和验证期径流过程图

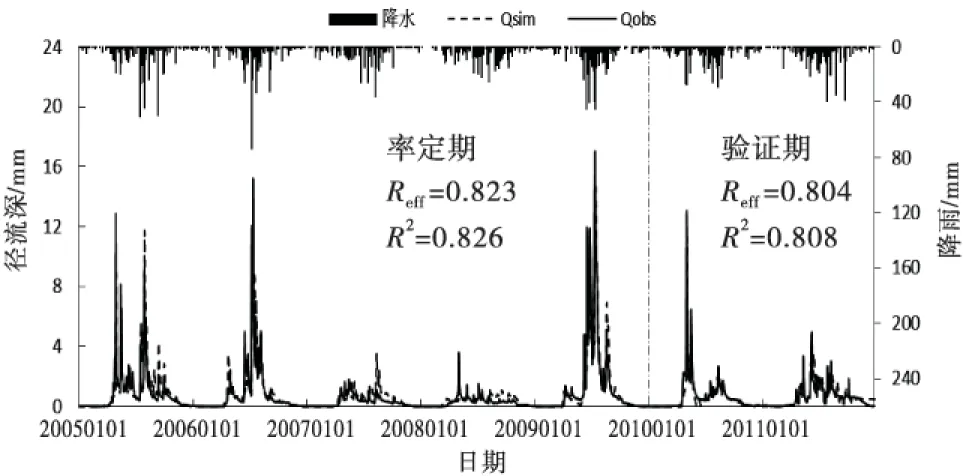
图6 伊春站率定期和验证期径流过程图

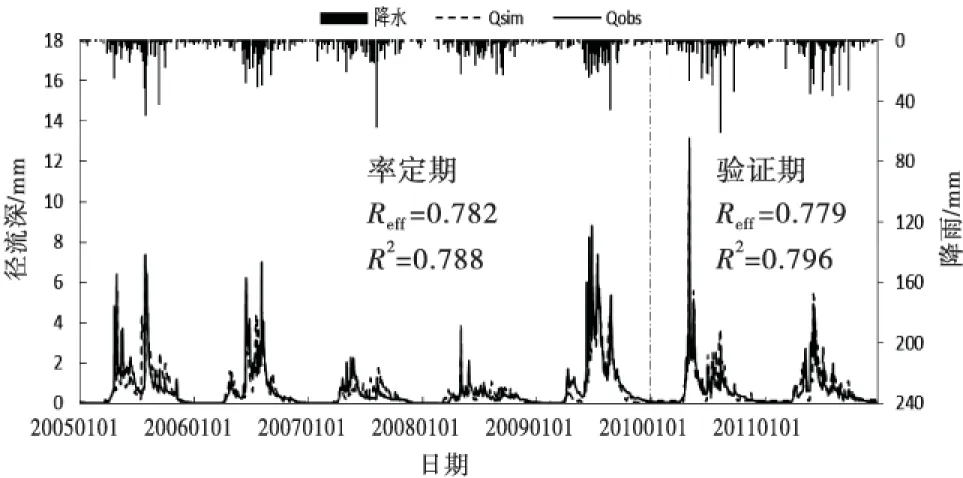
图7 南岔站率定期和验证期径流过程图

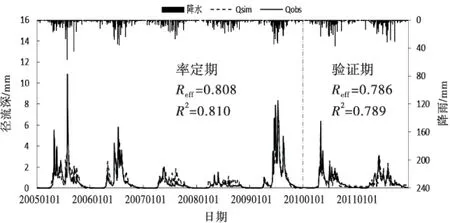
图8 晨明站率定期和验证期径流过程图

在模型率定期，除了南岔站的Reff和R2约为0.78，其余站的Reff和R2均大于0.80；在模型验证期，4个站的Reff和R2均约为0.80，其中南岔站的Reff略小，不到0.78，由于南岔站位于南岔河支流上，降雨资料较少，因此南岔站模拟精度略低．整体来讲，率定期的Reff和R2略高于验证期．结果表明HBV模型在汤旺河流域模拟和验证情况均较好，模拟径流过程线与实测径流过程线较为吻合．HBV模型在研究区有很强的适用性．

4 径流对不同气候情景的响应

根据所得各站模型参数，在此基础上改变模型输入的逐日平均气温(T)和逐日降水(P)数据，比较各种情形下流域多年平均径流深的差异，用相对误差(r)作为衡量指标，以此来研究气候变化对汤旺河流域径流的影响．相对误差计算公式由式(5)给出，以下游的晨明站为例，具体计算结果参见表4，绘制的降水变率与径流深变率关系如图9所示，温度变化与径流深变率关系如图10所示．

(5)

式中，Q为原始的多年平均径流深(mm)，Qi为气温和降水变化条件下的多年平均径流深(mm)．

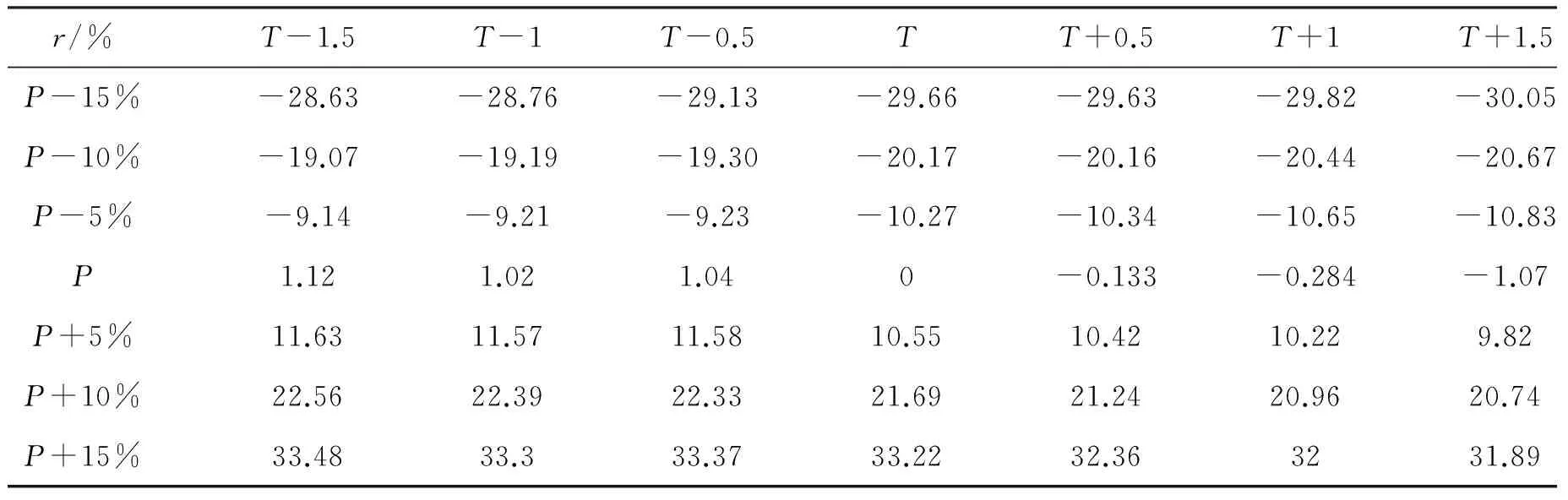
表4 晨明站多年平均径流深相对误差统计表 (单位：%)

图9 降水变率与径流深变率的关系图

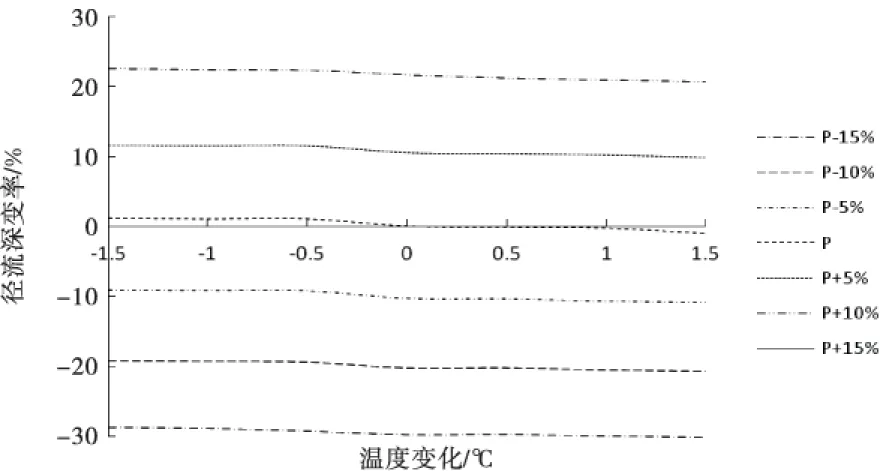
图10 温度变化与径流深变率的关系图

从表4中可以看出来，降水的改变对HBV模型模拟的多年平均径流深产生较为显著的影响．当气温固定不变，降水增加5%时，该流域多年平均径流深增量约为24.4 mm．当降水固定不变时，气温增加0.5℃，该流域多年平均径流深增加约0.68 mm．从图和计算结果中都可以看出，降水的变化对多年平均径流深的影响更大一些．因此，气候变化可以对流域内径流过程产生巨大的影响，准确地预报气候尤其是降水的变化可以合理地调配流域内的水资源．

5 结 论

1)参数敏感性分析结果显示，HBV模型中响应模块(K0、K1、K2、UZL)和汇流模块(MAXBAS)的参数最为敏感，土壤模块参数(BETA、LP)较敏感，对模型结果的影响较大，其余参数不敏感．2)HBV模型在汤旺河流域模拟效果理想，4个站的Nash-Sutcliffe效率系数Reff和确定性系数R2均达0.77以上，能较好地模拟径流变化过程，并且能较好地模拟洪水对降雨的响应过程，说明模型在东北地区具有较好的适用性．并通过研究径流对不同气候情景的响应，发现降水的变化较气温对汤旺河流域的水文循环影响更大．

[1] 赵彦增，张建新，章树安，等．HBV模型在淮河官寨流域的应用研究[J]．水文，2007，27(2)：57-59．

[2] 靳晓莉，张 奇，许崇育．一个概念性水文模型的参数区域化研究：以东江流域为例[J]．湖泊科学，2008，20(6)：723-732．

[3] 高红凯，何晓波，叶柏生，等．1955-2008年冬克玛底河流域冰川径流模拟研究[J]．冰川冻土，2011，33(1)：171-181．

[4] 王有恒，谭 丹，景元书．HBV水文预报模型在白龙江流域的应用研究[J]．水土保持通报，2015，35(3)：218-221．

[5] 周以良．中国小兴安岭植被[M]．北京：科学出版社，1994．

[6] 张洪斌，李 兰，赵英虎，等．HBV模型的改进与应用[J]．中国农村水利水电，2008，(12)：70-72．

[7] 王有恒，谭 丹，景元书．HBV水文预报模型在白龙江流域的应用研究[J]．水土保持通报，2015，35(3)：218-221．

[8] 李 胜，梁忠民．GLUE方法分析新安江模型参数不确定性的应用研究[J]．东北水利水电，2006，24(2)：31-33．

[9] 黄国如，解河海．基于GLUE方法的流域水文模型的不确定性分析[J]．华南理工大学学报：自然科学版，2007，35(3)：137-142．

[10] Beven K，Binley A． The Future of Distributed Models： Model Calibration and Uncertainty Prediction[J]．Hydrological Processes，1992，6(3)：279-298．

[11] 戴健男，李致家，黄鹏年，等．新安江模型参数不确定性分析[J]．河海大学学报：自然科学版，2011，39(6)：618-622．

[责任编辑 周文凯]

Application of HBV Model to Tangwang River Basin

Li Haichuan1Hao Zhenchun1NIMA Danzeng2Zhao Siyuan3Sun Aili1

(1. State Kay Laboratory of Hydrology-Water Resources & Hydraulic Engineering, Hohai Univ., Nanjing 210098, China; 2. Shannan Branch, Tibet Autonomous Region Hydrology Bureau, Shannan 856000, China; 3. Ningbo Planning & Design Institute of Water Conservancy & Hydropower, Ningbo 315192, China)

The conceptual semi-distributed rainfall model, HBV, is examined in the Tangwang River basin; and it is applied to simulate the daily runoff in order to evaluate the applicability of the model in the area. The parameters of HBV are calibrated and validated based on the sensitivity analysis; and the annual variation characteristics of runoff and precipitation are analyzed. Some kinds of hypothetical scenarios in the case of Chenming station are chosen to analyze the effects of precipitation and temperature on runoff. The results show that the response module parameters(K0、K1、K2、UZL) the bus module parameter(MAXBAS) were the most sensitive, and the soil module parameters(BETA、LP) are inferior sensitive. The simulation effect of HBV in Tangwang River basin is ideal. TheReffandR2of four site control river basin are all over 0.77. Besides, the response of flooding to precipitation can be simulated better to HBV model. Both of these indicated that the model could be successfully applied to Northeast China region; the changes in precipitation have a greater impact on runoff. And the changes of precipitation in the Tangwang River basin have a greater role in hydrological cycle than the temperature.

Tangwang River basin； HBV model； parameter sensitivity； hydrological responses

10.13393/j.cnki.issn.1672-948X.2016.05.005

2016-06-06

国家自然科学基金项目(41371047)；中国科学院战略性先导科技专项(XDA05110102)；水文水资源与水利工程科学国家重点实验室专项经费(1069-514031112)；江苏省普通高校研究生科研创新计划项目(KYLX_0464)；中央高校基本科研业务费专项(2014B34614)

李海川(1993-)，女，硕士研究生，从事融雪径流模拟研究．E-mail：lihaichuanxll@163.com

TV124

A

1672-948X(2016)05-0024-05