爆破地震波引起远场拱坝振动的数值模拟

吴浩然 刘晓青 宁昕扬

(河海大学 水利水电学院， 南京 210098)



爆破地震波引起远场拱坝振动的数值模拟

吴浩然 刘晓青 宁昕扬

(河海大学 水利水电学院， 南京 210098)

针对在爆破地震波数值模拟中，存在毫米级网格尺寸将导致模型网格数量巨大而无法计算的问题，采用等效爆破荷载法，避开传统方法中对炮孔形状的模拟，忽略对近场范围内结构的精确模拟，在保证振速峰值精度基础上适当增大网格尺寸，实现对爆破地震波引起处于爆破远场拱坝振动的数值模拟．最终，坝体振速峰值与实测值对比表明，二者符合较好，满足大坝爆破振动安全控制标准，可以作为类似工程爆破振动数值模拟的参考．

爆破地震波； 等效爆破荷载； 坝体振速峰值； 爆破远场

改扩建工程已成为大多数已建水电站减少弃水，提高水量利用系数，充分利用水能资源的主要途径．爆破开挖则是改扩建工程中，普遍采用的施工方法．爆破产生的地震波会引起附近建筑物振动，影响其安全运行．因此，有必要针对爆破地震波引起大坝振动的问题进行研究，确保坝体振速峰值在安全标准控制范围以内．

数值模拟爆破地震波作用下坝体振动响应，关键在于对爆破荷载施加的模拟．传统爆破荷载施加方法主要有两种：一是利用炸药参数及其状态方程建立炸药模型，模拟爆轰过程；二是由炸药参数确定作用在炮孔壁上的爆轰压力峰值，以及爆破荷载时程曲线，将半理论半经验爆破荷载时程曲线直接施加在炮孔壁上[1]．以上两种方法在建模时30都需模拟炮孔．同时，为精确模拟爆破近场结构的动力响应过程，张社荣等[2]提出网格尺寸应为炸药半径的1/3．考虑到炮孔直径通常为50 mm左右，则模型网格尺寸应小于20 mm．模拟处于爆破远场的高拱坝时，场地范围方圆数百米，坝体体积巨大．而对于拱坝这种高次超静定结构，又无法像重力坝或者土石坝一样，取典型坝段模拟其整体爆破地震响应，以减少网格数量．若模型网格尺寸小于20 mm，将使模型网格数量巨大，导致计算耗时过长甚至无法进行计算．因此有必要研究更经济有效的爆破荷载施加模拟方法．

为此，许红涛等[1]提出等效爆破荷载法，将等效爆破荷载时程曲线施加在同排炮孔连心线上，施加范围为整个装药深度，不需要采用毫米级网格模拟炮孔及近场结构；姚强等[3]采用等效荷载法，研究了地下厂房爆破施工对围岩稳定影响；阳生权等[4]结合施工隧道爆破地震作用下的围岩应力场和位移场，对既有隧道及两隧道间围岩进行了线性动力分析．实践证明，等效爆破荷载法建模简单易行，对处于爆破中远区范围(爆源距建筑物超过40 m)结构的爆破地震响应模拟效果较好．但在爆心距超过100 m且比例距离大于40 m·kg-1/3条件下[5]，对于爆破地震波引起拱坝振动问题的研究并不多见．

另外，考虑到爆破地震波在岩体阻尼作用下，高频成分衰减快，爆破振动主频总体向低频区域偏移[6]，引起处于远场范围拱坝振动的主要是低频波，故网格尺寸可以适当放大．

鉴于此，本文采用等效爆破荷载法模拟爆破荷载施加．在保证计算值与实测值相符的条件下，经试算适当加大网格尺寸，保证爆破地震波低频波较好模拟精度，降低模型网格数量．在地基范围较广、建筑物体积巨大以及爆破比例距离较远的条件下，对爆破地震波引起拱坝振动进行数值模拟．

1 工程概况

某水电站利用已建水电站汛期弃水发电，与已建水电站共用水库大坝．大坝布置在主河床，为混凝土双曲拱坝，最大坝高140.00 m，坝顶高程305.00 m，坝顶中心线弧长280.71 m．电站建成后，已建水库水量利用系数将由83.88%提高到88.99%，能有效减少水库弃水，更好地利用水资源．

该水电站厂房为地下厂房，是已建水电站的扩建工程，需要在拱坝左岸坝肩岩体里进行大规模地下工程爆破，包括主厂房、引水隧洞及施工支洞等位置的爆破施工．爆破位置距离已建大坝最小距离为53 m，最远超过100 m．

2 等效爆破荷载

在实际爆破工程中，爆破荷载的形式主要有半理论半经验的指数衰减型荷载[7-8]和三角形荷载[9-12]两种．在地下厂房开挖爆破施工中，为控制开挖边界，爆破一般不会造成围岩产生破碎性损坏，围岩基本处于弹性工作范围．因此，爆破荷载形式选用三角形冲击荷载，施加在开挖边界上．

确定三角形冲击荷载的关键，在于确定爆破荷载峰值、爆破荷载升压作用时间和正压作用时间，如图1所示．

图1 三角形冲击荷载

文献[13]给出了升压作用时间和总作用时间计算式：

(1)

(2)

在不耦合连续装药条件下，初始应力最大值，即爆破荷载峰值按照下式进行计算[2，8]：

(3)

式中，ρe为炸药密度；D为爆炸速度；dc为药径；db为孔径．

等效荷载法依据圣维南原理，对爆破荷载进行等效，并施加在同排炮孔连心线上．假定作用在单个炮孔壁上的爆轰压力为P0，炮孔半径为r0，相邻炮孔间距为a，由力和力矩平衡的原理，可将作用在炮孔壁上的爆轰压力P0等效为Pe施加在炮孔连心线上，如图2所示．等效压力Pe为：

(4)

图2 爆破荷载等效施加示意图

3 数值模拟

3.1 计算模型

建立水电站大坝和地基的三维有限元模型．地基高度取1.5倍坝高，上游自坝体向外延伸约1.5倍坝高，下游及左右岸均自坝体向外延伸约2倍坝高．模型具体尺寸为785 m×600 m×360 m，坝体和地基均采用六面体单元，共计694 375个结点，662 520个单元．建模时将地基范围内的地质构造(如断层或夹层)适当简化，并根据坝体混凝土材料分区和基岩力学参数，对模型单元进行分组．

(5)

(6)

(7)

式中，KBN和KBT分为人工边界弹簧的法向刚度和切向刚度；R为爆源至人工边界距离；cS和cP分别为S波和P波波速．整体有限元模型如图3所示．

图3 整体有限元模型

3.2 爆破荷载

爆破方案采用毫秒微差爆破．同时，由于厂房是由地下洞室群组成，具有边墙高、洞室数量多、交叉多、工程布置集中且与已有建筑交错等特点，地下厂房需要爆破开挖的位置较多．如果将所有爆破点全部建模分析，则计算量大，求解效率低．考虑到本文主要关注的是爆破对坝体的最大影响，故只选择典型工况进行分析．依据爆破位置距离坝体相对较近且装药量较大，同时兼顾主厂房位置的原则，选取典型工况如下：

工况1：厂房Ⅰ层中导洞0-29.35～0-30.95位置爆破；

工况2：引水隧洞0+116.7～0+115.5位置爆破；

工况3：Ⅰ号施工支洞0+108.8～0+110.6位置爆破．

将前述的等效爆破荷载施加在模型上，在仅有爆破荷载作用情况下分析大坝爆破地震响应．先以工况1为例验证本节所用模拟方法的可行性和正确性．

《水工建筑物抗震设计规范》[15]规定：“除水工钢筋混凝土结构外，水工建筑物在抗震计算中，其混凝土动态强度和动态模量的标准值，可较其静态标准值提高30%”．照此标准，厂房Ⅰ层中导洞0-29.35～0-30.95位置岩石及坝体材料参数见表1，爆破参数见表2．

据公式(1)、(2)以及上述参数可算得三角形爆破荷载见表3．

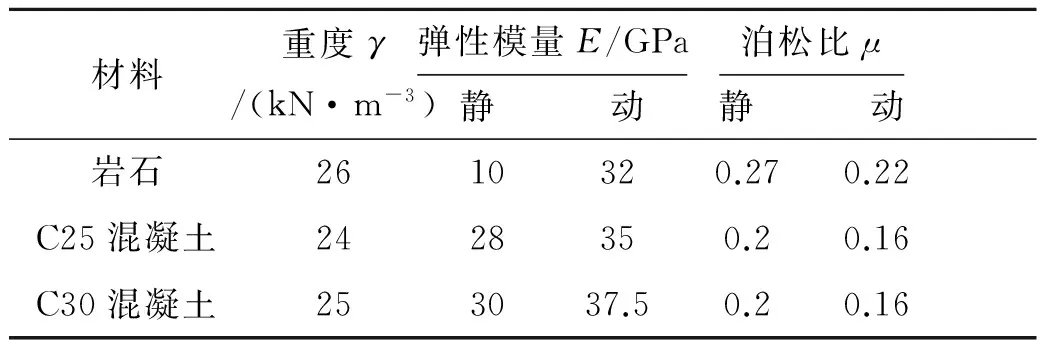
表1 岩石及坝体材料参数

表2 工况1爆破参数

表3 工况1三角形爆破荷载参数

文献[16]通过实地监控测量得到工作面附近的爆破振动速度时程曲线，反映出升压作用时间极短，且正压作用时间约为升压作用时间的5～8倍，由此将公式计算结果修正为ta=1 ms，tb=8 ms．

3.3 结果分析

爆破地震波作用下，测点处坝体各个方向振速时程曲线如图4～6所示，坝体最大振速计算值与实测值见表4．

图4 2号坝段坝顶x方向振速(工况1)

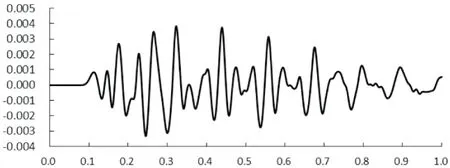
图5 2号坝段坝顶y方向振速(工况1)

图6 2号坝段坝顶z方向振速(工况1)

监测位置方向实测最大振速/(cm·s-1)计算最大振速/(cm·s-1)2号坝段坝顶x0.26340.2972y0.30430.3842z0.29250.2928

从图4～6可知，振速波动有一个先较快增大后较缓减小的过程，与所施加的爆破荷载变化规律相符，但是频率偏低，这是由于加大了网格尺寸使得爆破地震波中高频部分缺失．由表4可见各方向计算振速与实测振速数量级一致，说明对引起坝体振动起主要作用的低频部分得以展现．可见，基于等效爆破荷载法并适当加大网格尺寸的模拟方法，应用于爆破地震波引起远场拱坝振动模拟是可行的．同时，计算最大振速值稍大于实测最大振速值，这是由于模型采用的是线弹性材料而忽略了实际岩土体材料的阻尼效应，能量耗散速率慢，放大了振动效应．由此本文所用模拟方法的正确性得以验证，且从爆破振动安全控制角度来说，本文方法偏安全．

坝体振速峰值计算结果见表5．由表5知：坝体x方向最大振速为0.85 cm/s，坝体y方向最大振速为1.15 cm/s，坝体z方向最大振速为0.58 cm/s，均小于安全振速控制标准(7 cm/s)[15，17-19]．由此说明厂房Ⅰ层中导洞(0-29.35～0-30.95)位置爆破施工引起的坝体坝体振动在规范允许范围之内．

表5 坝体振速峰值(工况1)

爆破引起坝体第一主应力如图7所示，最大值为0.064 MPa．结果显示，计算值比实测值稍大，基于等效爆破荷载法并适当加大网格尺寸的模拟方法，应用于爆破地震波引起远场拱坝振动模拟是可行而且正确的．从爆破振动安全控制角度来说，本文方法偏安全，具有一定实用价值，可以作为类似工程借鉴．

图7 坝体第一主应力(工况1)

4 拱坝爆破振动分析

4.1 自振频率

拱坝自振特性分析计算结果见表6．

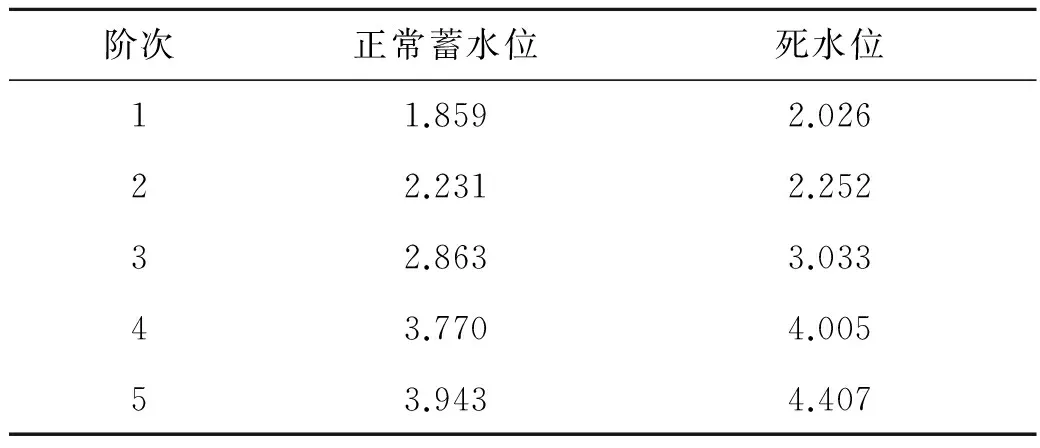
表6 坝体自振频率 (单位：Hz)

对坝体振动响应来说，爆破地震波低频部分贡献大，高频部分贡献小，正常蓄水位情况下该拱坝的第一阶自振频率为1.859 Hz，而爆破地震波引起坝体振动的实测主振频率至少为几十赫兹[17，20]，两者相差较大，不会引起坝体共振．

4.2 静力计算结果

坝体主应力特征值见表7．荷载组合1(正常温降)：正常蓄水位上下游静水压力+设计正常温降+自重+淤沙压力；荷载组合2(校核温升)：校核洪水位上下游静水压力+设计正常温升+自重+淤沙压力．

表7 坝体主应力特征值

静力计算表明，荷载组合1作用下坝体最大拉应力为3.63 MPa，荷载组合2作用下坝体最大拉应力为2.74 MPa．

4.3 最大振速与应力增量

按照第3节对工况1的模拟方法依次计算工况2、3相应的爆破地震波引起坝体振动响应参数，各方案爆破参数见表8，计算结果见表9．

表8 各爆破方案最大药量段别爆破参数

表9 爆破荷载作用下坝体响应

由于缺少爆破地震波作用下水工建筑物应力变化的控制标准，考虑到模型为线弹性，可以做线性叠加分析．由表9可知，爆破荷载单独作用引起的坝体振速峰值为3.2 cm/s，出现在2号坝段坝顶处；坝体最大拉应力为0.182 MPa，占静力荷载组合1引起最大拉应力的5.01%；占静力荷载组合2引起最大拉应力的6.64%．通过与水工混凝土材料动态性能标准对比可以得知，爆破荷载对坝体应力的影响程度很小，大坝应力状态处于安全范围．

爆破地震波单独作用引起坝体的振速峰值为3.2 cm/s，远小于《GB 6722-2014爆破安全规程》[18]振动安全标准和某拱坝水电站工程可行性研究报告确定的安全振速控制标准值(7 cm/s)，大坝振速峰值处于安全范围．

5 总 结

传统的爆破施工模拟方法所解决的，往往是对处于爆破近场范围建筑物受爆破损伤和振动影响的问题．而本文面临的是爆破地震波引起处于爆破远场范围的高拱坝振动的问题．前者要求精确模拟近场结构受损情况，模拟范围较小，可以并且需要用较小的网格尺寸．而后者要求对建筑物整体进行模拟，场地尺寸较大，较小的网格尺寸将导致计算耗时长甚至无法计算．

本文基于等效爆破荷载法，适当加大网格尺寸，建立了某拱坝三维有限元模型，实现了对爆破地震波引起处于爆破远场拱坝振动的数值模拟，较好协调了网格尺寸过小造成计算困难与网格尺寸过大造成计算精度降低的矛盾，可为类似工程数值模拟提供借鉴．同时，本文将等效爆破荷载法的应用范围，推广到在爆心距超过100 m且比例距离大于40 m·kg-1/3条件下，对爆破地震波引起处于爆破远场的高拱坝振动的模拟，具有一定工程实用价值．

[1] 许红涛，卢文波，周小恒．爆破震动场动力有限元模拟中爆破荷载的等效施加方法[J]．武汉大学学报(工学版)，2008，41(1)：67-71．

[2] 张社荣，李宏璧，王高辉，等．水下爆炸冲击波数值模拟的网格尺寸确定方法[J]．振动与冲击，2015(8)：93-100．

[3] 姚 强，杨兴国，陈兴泽，等．大型地下厂房开挖爆破振动动力响应数值模拟[J]．振动与冲击，2014，33(6)：66-70．

[4] 阳生权．小线间距施工隧道爆破地震影响下既有隧道围岩线性动力分析[J]．工程爆破，1998，4(1)：1-6．[5] 魏海霞．爆破地震波作用下建筑结构的动力响应及安全判据研究[D]．青岛：山东科技大学，2010．

[6] 卢文波，张 乐，周俊汝，等．爆破振动频率衰减机制和衰减规律的理论分析[J]．爆破，2013(2)：1-6+11．

[7] 李 宁，Swoboda G．爆破荷载的数值模拟与应用[J]．岩石力学与工程学报，1994，13(4)：357-364．

[8] Swoboda G，Aenz G． Practical Considerations of Blasting Loading Using Numerical Modeling[C]．//Proc .6th Int. Conf. Numer. Methods Geomech. Insbrush，1988：1681-1688．

[9] 朱瑞庚，王雪峰．不耦合装药爆破孔壁压力的计算(一)[J]．爆破，1990，7(3)：1-4．

[10] 张正宇，张文煊，吴新霞，等．现代水利水电工程爆破[M]．第一版．北京：中国水利水电出版社，2003．

[11] 夏 祥，李俊如，李海波，等．爆破荷载作用下岩体振动特征的数值模拟[J]．岩土力学，2005，26(1)：50-56．

[12] Chen S G，Zhao J， Zhou Y X． UDEC Modeling of a Field Explosion Test[J]． International Journal of Blasting and Fragmentation，2000(4)：149-163．

[13] 刘国华，王振宇．爆破荷载作用下隧道的动态响应与抗爆分析[J]．浙江大学学报(工学版)，2004(2)：77-82．

[14] 谷 音，刘晶波，杜义欣．三维一致粘弹性人工边界及等效粘弹性边界单元[J]．工程力学，2007，24(12)：31-37．

[15] NBT 35047-2015，水电工程水工建筑物抗震设计规范[S]．

[16] 苏佳园．爆破荷载作用下衬砌背后空洞对隧道稳定性影响规律研究[D]．重庆：重庆交通大学，2013．

[17] 罗 忆，卢文波，陈 明，等．爆破振动安全判据研究综述[J]．爆破，2010，27(1)：14-22．

[18] GB6722-2014．爆破安全规程[S]．

[19] 甄育才．爆破震动荷载下水电站厂房的安全分析[D]．武汉：武汉大学，2005．

[20] 钟祖良，刘新荣，梁宁慧，等．质点振动速度与主振频率在爆破监测中的应用[J]．重庆建筑大学学报，2006(4)．

[责任编辑 王迎春]

Numerical Simulation of Arch Dam Vibration in Far-field Induced by Blasting Seismic Waves

Wu Haoran Liu Xiaoqing Ning Xinyang

(College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China)

Once blasting seismic waves are numerically simulated with millimeter-sized mesh, the vibrations of an arch dam in far-field induced by these waves would be difficult to calculate in terms of such great mesh numbers. An equivalent approach for the acting of blasting load is adopted in this paper. The traditional modeling of the blast-hole shape is avoided, and the simulation accuracy of near-field construction vibrations is neglected as well. The mesh size is reasonably increased without an apparent decline in the simulation accuracy of the peak value of dam vibration velocity. Finally, it is found that the simulation results tally with the measured values, and that the safety control criteria of dam vibration velocity are satisfied at the same time. The paper could provide a reference for other similar numerical simulations of blasting vibration.

blasting seismic wave; equivalent blasting load; peak value of dam vibration velocity; far field of blasting

10.13393/j.cnki.issn.1672-948X.2016.05.003

2016-05-10

水利部公益性行业科研专项经费项目“高混凝土坝抗震安全研究”(201501034)

刘晓青(1965-)，女，教授，主要从事结构与流体静动相互作用方面的研究．E-mail：529783821@qq.com

TD235

A

1672-948X(2016)05-0014-05