基于改进HHT的微弱故障信号特征提取方法
周小龙,姜振海,马风雷
(1.东北电力大学 工程训练教学中心,吉林 吉林 132012;2.长春工业大学 机电工程学院,长春 130012)
基于改进HHT的微弱故障信号特征提取方法
周小龙1,姜振海2,马风雷2
(1.东北电力大学 工程训练教学中心,吉林 吉林 132012;2.长春工业大学 机电工程学院,长春 130012)
针对微弱故障信号故障特征难以提取的问题,提出一种基于改进希尔伯特-黄变换的故障特征提取方法。该方法首先采用平均总体经验模态分解将故障信号分解成一系列固有模态函数,再选取对故障特征敏感的固有模态函数进行希尔伯特谱和边际谱分析,从中提取故障特征。仿真和实际试验证明:希尔伯特谱和边际谱能够清晰呈现故障信号时域和频域内的细微特性,为微弱故障信号的特征提取提供了一种切实可行的方法。
希尔伯特-黄变换;平均总体经验模态分解;微弱信号;特征提取
在机械传动设备中,当某一零件出现早期缺陷时,其振动信号十分微弱,往往被其它零部件的运行振动信号和背景噪声所淹没,为故障的检测和诊断带来困难[1]。若设备中出现早期故障而不及时处理,将使机械传动设备无法平稳传动,并有可能造成有关部件报废。因此,研究机械设备微弱故障信号的特征提取方法具有重要意义。
在机械传动过程中,由于转速不稳定、负荷变化和环境噪声等因素的影响,其振动信号表现出非平稳和非线性的特征。目前对此类信号的故障特征提取与诊断常采用倒频谱分析、共振解调、时频分布和小波变换等方法[2]。其中,以小波变换的应用最为广泛[3-4]。由于小波变换的本质是可调的窗口傅里叶变换,在对信号作相关变换时会产生能量泄漏,同时基函数选择困难,使得该方法在获得较高精度的故障特征时存在很大困难[5-6]。希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是近年来由Huang[7]等人提出的一种分析非平稳和非线性信号的有效方法。由于HHT方法能自适应地将复杂信号分解成一系列包含信号特征的固有模态函数(Intrinsic Mode Function,IMF),突显信号局部特性,因此被广泛应用于微弱故障信号诊断领域。苏中原[8]等人针对周期平稳类微弱故障信号难以检测的问题,提出了基于HHT的故障信号检测方法;杨露[9]等人通过对比研究指出,对于故障引起包络变化的信号,在故障特征提取有效性方面,HHT明显优于小波变换;熊炘[10]等人使用HHT有效地提取出了转子径向摩擦故障信号的时频特征;刘继承[11]等人采用形态滤波和HHT相结合的方法准确检测出了由滚动轴承内圈故障所引起的故障特征频率。
虽然HHT方法在该领域有明显优势,但其仍有不足,这些不足会限制它在相关领域的进一步发展。具体表现:(1)由于信号间断性,出现了模态混叠问题,即同一个IMF中包含不同的频率成分;(2)对于机械故障诊断而言,通常只有部分IMF包含故障信息,其它IMF为噪声成分或干扰成分。因此,如果上述问题不解决会使Hilbert谱所提取的故障特征不明显,同时降低故障诊断精度。
基于上述分析,本文提出一种基于平均总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)和敏感IMF判别算法相结合的微弱故障信号特征提取方法。EEMD能有效避免经验模态分解(Empirical Mode Decomposition,EMD)的模态混叠现象,敏感IMF判别算法能去除虚假IMF分量,突显信号的故障特征。仿真和实际试验证明了该方法能有效提取故障信息,达到早期检测和诊断的目的。
1 改进HHT
HHT方法主要由EMD和Hilbert变换两部分组成。但是,EMD在分解信号的过程中存在模态混叠问题。该问题会使EMD分解出的IMF分量失去真实的物理意义,难以表征信号特征;而由IMF分量经Hilbert变换所得的Hilbert谱的精确性与诊断精度都会明显降低。为解决该问题,WU[12]等人提出了EEMD分解法。
1.1 EEMD
通过EMD分解,可以将任何复杂信号分解成一系列从高频到低频表示该信号特征时间尺度的IMFs。EMD分解其实也是一个信号“筛分”的过程,将信号x(t)作为待处理信号,最终可分解为
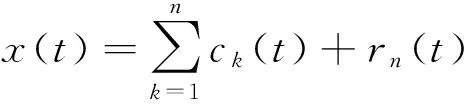
(1)
式中:c1,c2,…,cn为获得的n阶IMF;rn为残余分量。
EEMD的实质是一种在信号中加入噪声的辅助分析方法[13]。其具体分解步骤如下:
(1)初始化总体平均次数K和加入的噪声幅值,并使k =1;
(2)给待分析的信号x(t)加入给定幅值的白噪声nk(t),
xk(t)=x(t)+nk(t) ,
(2)
式中:x(t)为第k次加噪后的信号;nk(t)为第k次加入的白噪声;k =1,2,…,K;
(3)对x(t)进行EMD分解,得到一组IMF cn,k(n=1,2,…,N);其中,cn,k为第k次分解得到的第n阶IMF;
(4)如果k (5)计算K次分解的IMF的总体均值yn并作为最终IMF, (3) 式中:n =1,2,…,N;k =1,2,…,K。 将白噪声加入到信号中,会使信号在不同尺度具有连续性,并对多次分解的IMF进行总体平均来抵消噪声,这样既可获得准确的IMF又消除了所加入噪声的影响,从而有效地避免了模态混叠问题。 1.2 敏感IMF判别方法 经EMD分解出的IMF分量与原信号满足正交性,所以IMF分量应与原信号有较高的相关系数,相关系数越高,IMF分量所含信号物理特征越多,将其作为敏感分量进行故障诊断,具有更高的准确性和有效性。因此,根据故障信号与其IMF分量的相关系数以及其IMF分量与不含故障的正常信号的相关系数来判别对故障信息敏感的IMF分量。其具体步骤如下: (2)计算故障信号各IMF分量与正常信号的相关系数βi; (3)计算两者的差值,并定义为敏感系数 (4) (4)根据敏感系数λi选取门限阈值,剔除虚假IMF分量。 该方法不仅考虑了IMF与故障信号的相关性,同时也考虑了与正常信号的相似性。因此,能够削弱与故障特征无关的虚假成分,突显故障特征。 1.3 Hilbert分析 对EEMD所求出的每个敏感IMF分量进行Hilbert变换后可得Hilbert谱: (5) 式中:Re代表取实部,同时省略了残余项r;a(t)=[x(t)2+Y(t)2]1/2;x(t)、Y(t)分别为IMF分量的Hilbert变换与逆变换。 对上式积分,可得Hilbert边际谱: (6) 式中:T为信号x(t)的长度。 Hilbert谱能够准确反映时间、频率和能量三者的关系,由于IMF分量为边际谱的基函数,所以边际谱可有效消除虚假谐波分量,获得信号真实频率与振幅的分布[14]。 由于齿轮裂纹早期发生在个别齿上,故障信号十分微弱;同时,齿轮裂纹为齿轮局部故障,会产生冲击脉冲,裂纹齿啮合刚度降低,呈现出循环平稳特性[8]。从Hilbert谱中可以分析出,齿轮故障信号的能量随时间和频率的变化规律,提取故障特征,达到故障的早期诊断。 为验证改进HHT方法的有效性,仿真一个齿轮裂纹故障信号 x(t)=15cos(2πf1t+2cos(2πf2t))+3cos(2πf3t)+r(t), 图1 仿真信号频谱 图2 仿真信号Hilbert谱 式中: f1=150 Hz, f2=20 Hz, f3=50 Hz,r(t)为背景噪声;采样频率为1 024 Hz;采样时间为1 s。 对仿真信号进行小波降噪,采用通用阈值函数(sqtwolog),db5小波,5层分解。仿真信号的频谱,如图1所示。 在图1中,50 Hz、100 Hz、130 Hz等频率处都存在谱峰,但从中很难提取故障特征,这势必会增加信号诊断的误判几率。经改进HHT得到的故障信号Hilbert谱,如图2所示。 由图2可知,故障信号的能量主要集中在两个区域内,其中主要能量是以频率为f1=150 Hz为中心分布,并呈现出周期性,其振动周期为50/1 024≈0.049 s,即调频为1 024/50≈20 Hz。同时,在f3=50 Hz处也有能量分布。由上述分析可知,改进HHT方法能够有效提取仿真信号的故障特征。 滚动轴承是旋转机械中应用最广泛的部件之一,它的运行状态直接影响着整个机械系统的性能。滚动轴承早期故障信号十分微弱,通常会淹没在其它部件的振动信号和环境噪声中,难以识别。 为验证方法的正确性,在滚动轴承故障模拟实验台上进行了正常和内圈存在点蚀故障状态下的试验。试验过程中,加速度信号由16通道数据记录仪采集,采样频率为12 kHz,采样时间为1 s。经计算得到,内圈故障特征频率为162 Hz。正常状态和内圈故障状态下采集到的加速度信号,如图3所示。从图3中可以看出,由于环境噪声的影响,所测信号中存在较大干扰。采用一维离散小波进行降噪处理,降噪后信号如图4所示。从图4中可以看出,小波降噪后,信号中绝大多数无用的高频分量都被去除,信号波形更加突显原信号的信息。轴承内圈故障信号与正常信号均表现为脉冲冲击,两种状态下的时域信号十分相似,从中无法找出内在规律。 图3 不同状态下轴承时域信号图4 小波降噪后不同状态下轴承时域信号 对降噪后轴承内圈故障信号采用EEMD分解,得到4个IMF分量,运用敏感IMF判别算法求出各IMF相关系数与敏感系数,如表1所示。 表1 故障信号各IMF相关系数与敏感系数 由表1可知,取门限阈值为0.2,则IMF1和IMF2为敏感IMF分量,而IMF3和IMF4是既包含故障信息又包含正常信息的虚假IMF,因此将它们剔除。对敏感IMF进行Hilbert变换,求出Hilbert谱和边际谱,如图5、图6所示。 从图5中可以明显看到,瞬时的高频冲击分量,故障信号的能量主要集中在归一化频率0.1-0.2之间,由于采样频率为12 kHz,故障信号能量主要集中在1 200 Hz-2 400 Hz的区间内,冲击成分的周期约为5.9 ms。从图9中可看到,在165 Hz处有较大的幅值,傅里叶频谱的幅值只能反映频率在信号中实际存在的可能性大小,而边际谱的幅值能真实反映频率在信号中是否存在[7]。因此,结合图5和图6可以判断轴承为内圈点蚀故障。 图5 轴承内圈故障信号Hilbert谱图6 轴承内圈故障信号边际谱 (1)Hilbert谱和边际谱能准确反映微弱故障信号时域和频域的细微特征,这是单独时域和频域分析方法无法得到的; (2)通过仿真和滚动轴承内圈故障诊断表明,基于改进HHT方法的微弱信号检测方法对微弱故障信号检测具有一定的分析能力。 [1] 段锦升.机械系统微弱故障信号检测及提取方法研究[D].太原:太原理工大学,2007. [2] 曾刚.滚动轴承微弱故障信号检测方法研究[D].成都:成都理工大学,2010. [3] 赵学智,叶邦彦,陈统坚.基于小波-奇异值分解差分谱的微弱故障特征提取方法[J].机械工程学报,2012,48(7):37-48. [4] 马伦,康建设,孟妍,等.基于Morlet小波变换的滚动轴承早期故障特征提取[J].仪器仪表学报,2013,34(4):920-926. [5] Lin J,Qu L.Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis [J].Journal of Sound and Vibration,2000,234(1):135-148. [6] 陈双喜,林建辉.基于改进HHT分析车轮椭圆化对高速列车时频特征的影响[J].振动与冲击,2013,32(11):126-130. [7] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proceeding of the Royal Society of London-Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995. [8] 苏中元,贾民平.基于希尔伯特-黄变换周期平稳类微弱故障信号检测[J].东南大学学报:自然科学版,2006,36(3):389-392. [9] 杨露,沈怀荣.希尔伯特-黄变换与小波变换在故障特征提取中的对比研究[J].兵工学报,2009,30(5):628-632. [10] 熊炘,杨世锡,甘春标.运用BF-HHT的转子径向摩擦故障特征提取方法[J].振动、测试与诊断,2012,32(2):192-196. [11] 刘继承,聂品磊,杨宏宇,等.基于形态滤波和HHT的滚动轴承故障特征提取[J].化工自动化及仪表,2014,41(5):529-532. [12] WU Z H,HUANG N E.Ensemble empirical mode decomposition:A noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41. [13] 游于跃,王宁,李明明,等.基于EEMD和BP神经网络的风机齿轮箱故障诊断方法[J].东北电力大学学报,2015,35(1):64-72. [14] 钟佑明,秦树人.希尔伯特-黄变换的统一理论依据[J].振动与冲击,2006,25(3):41-43. Feature Extraction Method for Weak Fault Signal Based on Improved HHT ZHOU Xiao-long1,JIANG Zhen-hai2,MA Feng-lei2 (1.The Engineering Training Teaching Lenter,Northeast Dianli University,Jilin Jilin 132012;2.Electrical Engineering College,Changchun University of Technology,Changchun 130012) For solving the difficulty in extinction of weak fault signal,a method based on improved Hilbert-Huang transform is proposed.The weak fault signal is decomposed by ensemble empirical mode decomposition,and the intrinsic mode functions are obtained,then the sensitive intrinsic mode functions are selected by the sensitivity evaluation method.Finally,the Hilbert spectrum and marginal spectrum of the signals are obtained by the sensitive intrinsic mode functions,and the characteristics of the weak fault signal are detected.The simulation and actual experiment results show that the Hilbert spectrum and marginal spectrum can display the subtle features corresponding to time and frequency of weak fault signals,and offered a practical method for its feature extraction. Hilbert-Huang transform;Ensemble empirical mode decomposition;Weak fault signal;Feature extraction 2016-04-12 周小龙(1987-),男,吉林省长春市人,东北电力大学工程训练教学中心助理实验师,硕士,主要研究方向:机械精密加工与故障诊断. 1005-2992(2016)05-0052-05 TH17 A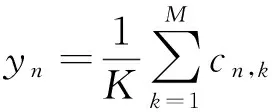


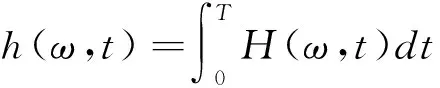
2 齿轮裂纹故障仿真分析


3 试验研究



4 结 论

