基于改进型积分分离式PID的机器人运动控制

孟祥萍，寇 磊，苑全德，皮玉珍

(1.长春工程学院 电气与信息工程学院，长春 130012；2.东北电力大学 信息工程学院，吉林 吉林 132012)



基于改进型积分分离式PID的机器人运动控制

孟祥萍1，寇 磊2，苑全德1，皮玉珍1

(1.长春工程学院 电气与信息工程学院，长春 130012；2.东北电力大学 信息工程学院，吉林 吉林 132012)

针对移动机器人在旋转角度控制时，普通PID控制器存在超调、波动和普通积分分离式PID存在响应速度慢的问题。提出了改进型积分分离式PID控制算法，采取对PID控制器的比例项和积分项同时进行控制的方法，并针对不同阶段误差采取参数自适应的控制。改进型积分分离式PID控制器避免了超调和波动，提高了系统的稳定性，同时又提高了系统的响应速度。与普通积分分离式PID相比，系统输入大约提前500 ms消除静差，系统响应大约提前400 ms消除静差。在机器人旋转控制时，避免了机器人的旋转波动，减少了对轮子的磨损，同时又能准确快速的旋转到目标方向。

改进型；积分分离式PID；移动机器人；运动控制

如今的自主机器人一般都具有了内外部传感器组成的先进的感知系统，不仅可以感知内部参数，还可以通过外部传感器，如GPS传感器、视觉传感器等，对外部信息进行感知、提取、处理，并做出合理的判断和动态决策。运动控制是其最基本，也是非常重要的一个环节。运动控制的主要目的是使机器人可以快速实现任意转角运动，调整姿态，沿着目标路径进行运动[1]。

PID控制技术广泛应用于工业控制的各个领域，在机器人运动控制中也经常采用PID控制技术[2]。文献[1]中采用模糊控制与PID控制相结合的方法，增强了控制器的调节能力，提高了机器人转角的精度。文献[3]在温度控制算法中采用了积分分离式PID，在保证积分作用的同时，又减小了超调。文献[4]提出了积分分离式分段PID控制复合控制算法，实现了系统的稳定控制，提高了系统姿态控制精度。文献[5]提出的基于状态反馈的自适应控制策略提高了移动机器人的轨迹跟踪性能和鲁棒性。文献[6]提出的基于模糊技术的PI控制器参数自整定控制算法具有较好的自适应性和鲁棒性。文献[7]采用模糊控制方法消除模型等不确定性因素的影响，提高了空间航天器的交会成功率和精度。文献[8]将方向偏差、方向偏差变化和两轮转速控制信号作为模糊集输入，采用模糊逻辑控制方法，使机器人获得良好的行走动态性能。文献[9]中采用积分分离PID控制算法调节伺服系统的位置，当被控制量与目标值偏差较大时，取消积分作用，以免由于积分作用使超调量增大，降低系统的稳定性，当被控制量接近目标值时，引入积分控制消除静态误差，提高控制精度。

本文先对移动机器人控制模型进行了分析，然后又对普通PID和积分分离式PID控制进行了论述，在积分分离式PID的启发下，提出了采用在比例项和积分项前乘以α，β，同时对比例项和积分项进行控制的改进型积分分离式PID控制算法，并受模糊逻辑控制算法启发，对误差进行分段控制，在不同误差的分段内采用不同的控制参数，提高系统的鲁棒性。最后对该算法进行了仿真和实验，采用改进后的积分分离式PID对机器人旋转时进行控制，减少了系统调节时间，提高了系统的稳定性和响应速度，增强了系统的鲁棒性。

1 控制系统模型

在对移动机器人进行有效控制时，需要先分析移动机器人的运动模型，这里采用的是独立双轮驱动的移动机器人，其运动情况如图1所示。图中，VL和VR分别为机器人左右轮的线速度，VC为机器人的质心线速度，w为质心的角速度，L为两轮的间距，x和y分别为机器人质心的二维平面坐标，θ为机器人相对于X轴坐标的夹角。机器人的位姿P和位置PC分别定义为：

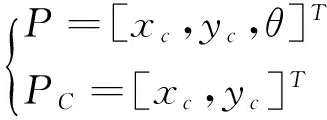
(1)

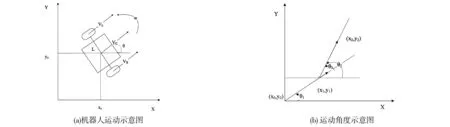
图1 控制系统模型

假定轮子在地面做纯滚动运动，即机器人瞬间与地面接触点的速度为0，则机器人的质心速度向量S为：

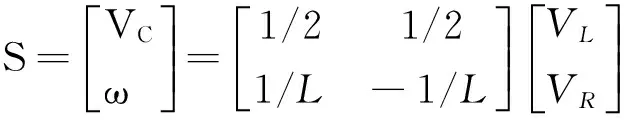
(2)

由于存在非奇异转换矩阵，可以通过控制机器人速度向量来改变机器人的位姿，从控制的角度来说，这两个向量等价，不难列出机器人的运动学方程[10-11]：

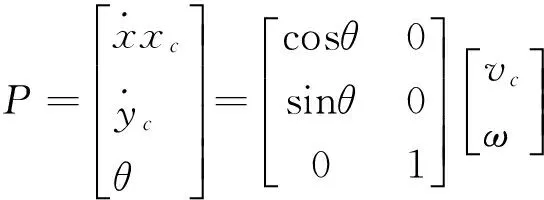
(3)

机器人的坐标由GPS传感器获得，机器人旋转角度由角度传感器测得[12-14]，根据图1(b)中所示坐标可以求得机器人目标旋转角度θ3，计算公式如下：

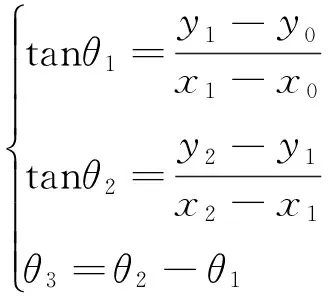
(4)

2 机器人运动控制

2.1 积分分离式PID控制

离散PID控制算法通常表示为：

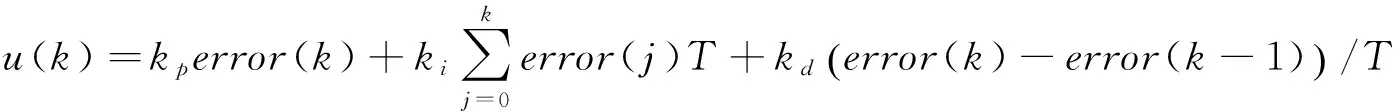
(5)

积分分离式PID控制算法为：

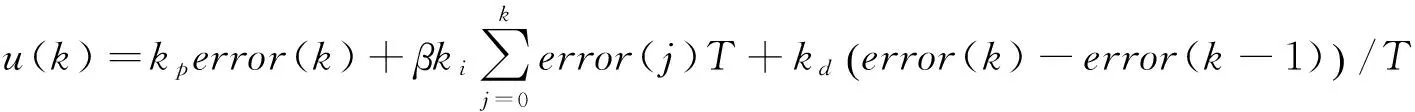
(6)

上式中error(k)=yd(k)-y(k)，error(k)为机器人目标旋转角度与实际旋转角度的误差，yd(k)为目标旋转角度，y(k)为实际旋转角度，即被控对象输出，u(k)为角度控制器，即被控对象输入。kp，ki，kd分别为控制器的比例、积分、微分控制参数，T为采样时间，β为积分项的控制系数。

在PID控制器中，比例环节主要是成比例的反映控制系统的偏差信号，反映在机器人旋转上即为目标旋转角度与实际旋转角度的误差，偏差一旦产生，控制器立即产生控制作用减小偏差。积分环节主要是为了消除静差，提高控制的精度。微分环节主要反映偏差信号的变化趋势，并能在偏差信号变得太大之前引入一个早期修正的信号，加快系统的动作速度，减少调节时间[15]。

普通PID在机器人的运动过程控制的起始、结束、或者大幅度的改变设定值时，较短时间内系统输出会有较大偏差，由于PID运算的积分积累，控制量超过执行机构允许的最大动作范围，系统将出现较大的超调或者较大的震荡，导致机器人原地摆动或者摆动幅度过大，损坏电机和轮子。积分分离式PID在机器人控制过程中避免了超调和波动的现象，但没能避免调节速度慢，响应时间长的缺陷。

图2 改进型积分分离PID控制框图

2.2 改进型积分分离式PID控制

根据PID控制器在比例控制中，kp加大，系统的动作灵敏提高，响应速度提高，kp偏大，振荡次数加多，调节时间加长[16]。当kp太大时，系统会趋于不稳定。如果kp太小时，又会导致系统的动作缓慢[17-20]。改进型积分分离式PID控制的基本思路是：当被控量与设定值偏差较大时，比例控制kp较大，ki较小，既保证了系统的稳定性，避免了超调，还适当的提高了系统的响应速度；当被控制量接近设定值偏差较小时，kp较小，ki较大，消除了静差，避免了超调和震荡，提高了控制精度。其具体实现步骤如图2所示，其基本形式如下：

改进型积分分离式PID控制算法如公式(7)所示，在比例项和积分项前分别加入α和β系数进行控制，从而实现比例和积分的同时控制。

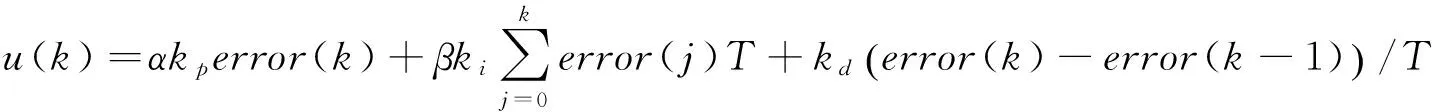
(7)

上式中α为比例项控制系数。

本文采用的机器人为双轮驱动的小车，在机器人运动时循迹和位姿控制是很重要的环节。这里循迹采用的GPS定位，预先设定好巡检线路，位姿控制主要说的是机器人的运动方向角的控制。在角度控制中使用改进型积分分离式PID进行控制，减少了机器人位姿的调整时间，机器人可以快速稳定的切换到预定的轨迹。

3 仿真与实验

本文以式(8)的被控对象进行仿真，该被控对象为一个二阶延迟系统。

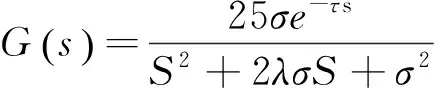
(8)

采样时间为20 ms，延迟4个采样时间，即τ=80 ms，初始kp=0.80，ki=0.005，kd=3.0，yd(k)=40，σ=18，λ=0.2，α，β参数如表1所示，分别对式(5)(6)(7)的PID控制器进行阶跃响应，仿真结果如图3所示。

图3 控制仿真图

分析图3中的(a)(c)(e)可知，采用积分分离方法控制效果相对于普通PID控制方法有很大改善，避免了超调。在(a)(c)中被控输入u(k)分别在2 000 ms和1 500 ms左右进入稳定状态，而在(e)中时间大约在700 ms进入稳定状态，可知采用改进型积分分离式PID在避免超调的同时，又使被控输入更快的进入稳定状态，加快调节速度。分析图3中(b)(d)(f)可知，采用积分分离式PID控制比普通PID产生更稳定的系统响应，避免了系统震荡，在系统响应稳定时间上改进不大，时间大约都在1 300 ms左右，而采用改进型积分分离式PID在避免系统响应震荡的同时，提高了系统响应速度，大约在700 ms进入系统响应稳定状态。综上所述可知，改进型积分分离式PID控制器既可以避免系统超调，保证系统稳定性，又可以有效的提高系统响应速度。

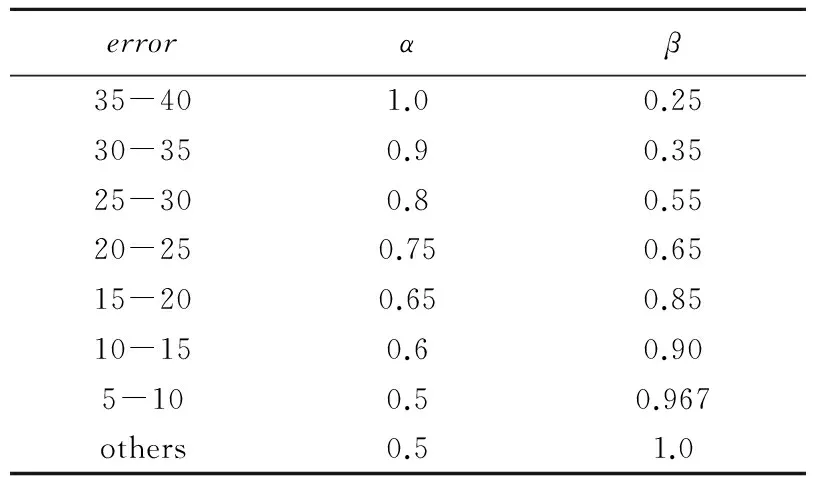
表1 参数控制表

图4(a)为被控输入u(k)的误差仿真图，(b)为阶跃跟踪y(k)的误差仿真图。由(a)可知，普通PID的被控输入出现了双向的波动，普通积分分离式PID与改进型积分分离式PID都避免了双向波动，但在进入稳态的时间(即误差为0的时间)，改进型积分分离式PID要提前500 ms左右。由(b)可知普通积分分离式PID与改进型积分分离式PID的响应都没有出现波动现象，在500 ms之后，由于改进型积分分离式PID削弱了比例作用，增大了积分作用，比普通积分分离式PID提前400 ms左右消除了静态误差，提前进入了稳定响应。

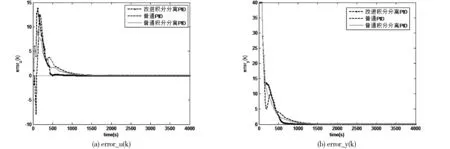
图4 误差分析图

图5 机器人运动轨迹

当机器人要旋转的角度较大时，即error的值较大的时候，α选取较大的值和β取较小的值，可以加快机器人的旋转速度；当error较小时，减小α的值增大β的值，降低了机器人旋转的速度，避免出现较大的超调，同时利用积分作用可以消除静差。在改进型积分分离PID控制下，机器人在控制左右轮的差速度时比较平稳，没有出现大幅度波动现象。图5为机器人在webots平台(机器人仿真软件)下的循迹导航效果图，机器人都是在(0，0)点附近出发，图5中在坐标(-15，15)处出现了较大误差，由于使用GPS导航，重新定位，后续的循迹基本没有出现偏差，循迹过程中坐标点之间的相关性不大。

4 结 论

本文对进型积分分离式PID控制算法的仿真，证明该算法可以弥补普通PID控制器超调和波动的缺陷，同时又比普通PID控制器和积分分离式PID控制器具有更快的响应速度，缩短了动态调整时间。对移动机器人进行的实验取得了很好的效果，机器人旋转稳定，调整位姿既快又准，从而再次证明了改进型积分分离式PID控制算法具有无超调，无波动，调整时间短，响应速度快以及很好的自适应性。

[1] 高健，黄心汉，彭刚，等.基于Fuzzy-PID的移动机器人运动控制[J].控制工程，2004，11(6):525-528.

[2] 王志勃，毕艳茹.机器人PID控制算法研究与实现[J].计算机技术与发展，2014，24(10):127-130.

[3] 夏敦柱，王寿荣，周百令.硅微陀螺仪零偏温度性能补控方法设计[J].东南大学学报，2012，42(2)：290-294.

[4] 刘治华，王春丽，杨硕，等.集成化储能/姿控飞轮系统控制方法实验研究[J].太阳能学报，2011，32(12)：1804-1809.

[5] 孙棣华，崔明月，李永福.具有参数不确定性的轮式移动机器人自适应backstepping控制[J].控制理论与应用，2012，29(9)：1198-1204.

[6] 李德军，张小栋，王云霞.轮式移动机器人行走的模糊比例积分控制方法[J].西安交通大学学，2008，42(1)：126-128.

[7] 张波，李海阳，唐国金.变时延遥操作交会的Smith模糊控制[J].物理学报，2013，62(2)：581-591.

[8] 张云洲，吴成东，薛定宇，等.自主移动机器人嵌入式控制系统研究[J].东北大学学报，2008，29(1)：29-32.

[9] 胡科峰，周云飞，李作清，等.基于积分分离的PID位置控制器的设计[J].机床与液压，2004(5):19-21.

[10] 张春晖，侯祥林，徐心和.足球机器人系统仿真中的数学模型[J].东北大学学报，2001，22(5)：493-496.

[11] 余群明，王会方，张骏，等.足球机器人运动控制算法研究[J].湖南大学学报：自然科学版，2006，33(6)：42-45.

[12] 房建成，申功勋，万德钧，等.GPS/DR组合导航系统自适应扩展卡尔曼滤波模型的建立[J].控制理论与应用，1998，15(3)：385-390.

[13] 周卫东，蔡佳楠，孙龙.GPS/SINS超紧组合导航系统自适应混合滤波算法[J].哈尔滨工业大学学报，2014，46(7)：47-52.

[14] Jan Wendel，Oliver Meister，Christian Schlaile，Gert F.Trommer，An integrated GPS/MEMS-IMU navigation system for an autonomous helicopter[J].Aerospace Science and Technology，2006，10(6):527-533.

[15] 周武能，田林林.基于模糊PID算法的无线分布式温度控制系统[J].控制工程，2014，21(3):309-314.

[16] 吴宏鑫，沈少萍.PID控制的应用与理论依据[J].控制工程，2003，10(1):37-42.

[17] 朱志强，江紫亚，何玉庆，等.PID控制器的频域特性与无模型参数调节[J].控制与决策，2014，29(10)：1833-1838.

[18] 李丽娜，柳洪义，罗忠，等.模糊PID复合控制算法改进及应用[J].东北大学学报，2009，30(2)：274-278.

[19] Mehdi Golestani，Iman Mohammadzaman，PID guidance law design using short time stability approach[J].Aerospace Science and Technology，2015，43(3):71-76.

[20] 张虹，于雷，胡波.基于改进PSO的励磁系统非线性PID控制研究[J].东北电力大学，2013，33(1/2)：152-155.

Motion Control of Robot Based on New Integral Separated PID

MENG Xiang-ping1，KOU Lei2，YUAN Quan-de1，PI Yu-zhen1

(1.School of Electrical Engineering and Information Technology，Changchun Institute of Technology，Changchun 130012；2.School of Information Engineering，Northeast Dianli University，Jilin Jilin 132012)

For the mobile robot to control the rotation angle，the general PID controller has the disadvantages of overshoot，fluctuation，and the ordinary integral separated PID has the problem of slow response speed.A new integral separated PID control algorithm is proposed that is used to control the PID controller's proportion and the integral term.The new integral separated PID controller avoids the overshoot and fluctuation，improves the stability of the system，and improves the response speed of the system.Compared with the ordinary integral separated PID，the system input approximately ahead of the 500ms to eliminate the static difference，the system response in advance 400ms to eliminate the static difference.When the robot rotates，the robot can avoid the rotation，reduce the wear and tear of the wheel，and can rotate to the target accurately and quickly.

Improved；Integral separated PID；Mobile robot；Motion control

2016-04-12

吉林省教育厅“十二五”科学技术研究项目(2014324)；长春市科技局项目(14KG026)；吉林省教育厅项目(No.2014339 and No.2014309)；吉林省科技厅项目(No.20150203002SF)

孟祥萍(1961-)，女，吉林省长春市人，长春工程学院电气与信息工程学院教授，博士，主要研究方向：智能控制理论及应用、电力系统安全性优化应用等研究.

1005-2992(2016)05-0086-06

TP24

A