社会网络中的社区挖掘算法研究
杨 成,杜文才,2
( 1.海南大学 信息科学技术学院,海南 海口 570228;2.澳门城市大学, 澳门 999078)
社会网络中的社区挖掘算法研究
杨 成1,杜文才1,2
( 1.海南大学 信息科学技术学院,海南 海口 570228;2.澳门城市大学, 澳门 999078)
结合点社区和边社区的优点,对边社区结构,采用网络中的局部信息进行挖掘,以边适应度和点相似性为基础,提出了新的社区挖掘算法.根据特定的中心性原则设定一条初始的边作为种子,为了得到该边所在的局部社区的社区结构,不断最大化一个适应度函数,并通过基于点相似性的模块度函数来进行边界点识别.
社交网络; 边适应度; 节点相似度; 社区挖掘
18世纪,瑞典数学家欧拉解决了柯尼斯堡问题,图论由此诞生,欧拉成为图论的创始人,之后更多的学者投入到对图的研究工作中.20世纪30年代开始,有些学者开始关注社会网络的研究工作,目前社会网络的研究是社会学领域中最受关注的研究方向之一[1].
随着互联网的普及,尤其是移动互联网的发展,各种类型的网络社交平台和应用相继出现,并产生了巨大的社会效应和经济效应,从传统的论坛到大热的博客和微博,再以微信为代表的移动社交应用拥有数亿的用户.在这个信息产生财富的年代,企业界尤其是互联行业逐渐重视起社会网络的分析,寄希望于挖掘隐藏在社会网络背后的信息、知识以及规律用以推动企业的发展[2].
文献[3]提出了一种指标作为社区结构的评价标准,构建社区结构的过程则是从给定节点出发以最大化指标作为社区挖掘的规则选取临近节点加入社区.文献[4]定义了局部社区模块度,以极大化局部社区模块度为聚类规则,合并满足聚类规则的邻接节点并迭代运算实现局部社区挖掘.文献[5]认为核心节点对网络的影响巨大,中心节点作为网络的核心节点,应围绕其展开社区挖掘,一方面能够提高社区挖掘的精确度,另一方面也更具有现实意义.文献[6]定义了社区和外部节点的连接相似度作为指标,通过迭代运算并在每次迭代过程中通过特定的剪枝算法提高精确度缩小运算范围,而迭代终止条件则为不能通过添加任何外部节点使模块度M增大.文献[7]通过网络根据一定的条件构建树,依据最大流最小割定理从给定节点出发对网络进行分割,从而实现社区挖掘.上述文献都是设定社区结构评价标准,在由初始节点向外部聚类的过程中,根据待合并节点带来的社区评价指标增益判断该节点是否应该纳入社区.此方法在聚类过程中往往忽略了待合并节点与外部邻接子图的连接情况,这就使得给定节点的位置以及评价指标设定会在很大程度上影响社区挖掘的结果,准确性和稳定性往往欠佳.
在此基础上,笔者提出了一种边社区挖掘算法,具有以下优点
1) 同时使用节点和边作为研究对象,突破传统社区挖掘使用节点作为出发点的惯性思维.
2) 提出了一种基于边适应度的聚类规则以应用于社区挖掘扩张过程.
3) 基于中心性原则选择初始种子边,有利于提高社区挖掘的速度并优化社区挖掘的结果.
4) 通过边界节点识别控制社区挖掘聚类过程,从而减少了由人工输入参数的不确定而导致的社区的范围和大小的差异.
1 问题分析与算法描述
目前比较普遍的社区挖掘方法将社区的本质视为节点集合,而在同一个集合内部的节点具有某种意义上的共性[8].首先构建某种社区结构评价指标,比如N-G模块度[9],在聚类的过程中根据最大化指标的原则判断节点的归属,从而最终完成社区挖掘.此类算法往往都基于较为基础的特性,其思想对学者们的研究具有巨大的启迪意义,很多新算法都会用到其思想,然而基础算法通常只适用于社区结构相对明显的复杂网络,有时会存在诸如以下的问题:1)初始节点的位置很大程度上影响社区挖掘的结果;2)对于聚类停止的条件难以判断,即便可以根据先验知识对评价指标设置阈值来控制聚类的终止,但是很多情况下难以得到精准的阈值.
基于上述分析,笔者提出了一种新的社区挖掘算法.算法分为边社区聚类和边界节点识别2个阶段,一方面根据边社区的特性通过分析社区邻域范围内连接紧密度从给定初始种子边出发展开社区挖掘;另一方面在对邻接边的聚类过程中,根据节点相似性对当前的边界节点进行判断,从而判断迭代的终止并在一定范围内控制社区的规模完成局部的社区挖掘;最后重复上述过程,最终找到整个网络的社区结构.
1.1 选择初始边 社区挖掘算法的结果往往对种子的位置比较敏感,从不同的初始种子出发得到的结果往往不同,所以初始种子的选取至关重要.有的社区挖掘算法通过随机选择初始种子,比如文献[10]通过随机算法选择一个节点作为种子,所以其结果具有一定程度的随机性.文献[11]通过选择网络中的最大子团作为初始的种子.但是团是一种非常严格的定义,在现实的社会网络中,很少能够观察到大规模的团,此外,团的结构非常不稳定,因为删除其中的任意一条边都会导致团被破坏.最重要的是寻找网络中的团特别是在大规模网络中寻找团,计算复杂度太高.
采用选取中心性较强的边作为初始的种子.基于这种考量,采用聚类系数对边进行排序,从中选取密度较大区域的边.
定义1 边聚类系数在网络中,由节点i和节点j构成了一条边,则此条边的边聚类系数定义为

(1)
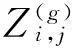
1.2 边的适应度函数 对于一个社区来说,质就是整个网络的一个子图.社区挖掘的算法就是寻找整个网络的一个子图,此子图内部的联系尽可能频繁和紧密,而子图与外部的联系则尽量稀疏.最极端的情况是网络的一个子图,该子图是个完全图并且与外部没有边.在以节点为中心的社区挖掘算法中,通常会定义一个适应度函数作为目标函数,从种子节点出发,通过不停地聚类使得目标函数的值持续增加,根据贪心算法的思想从候选节点集选出特定节点.适应度表示子图内部与外部的紧密度,增加和删除成员都会使这个子图的适应度值产生变化.社区挖掘的过程就是从种子出发不停地增加可以使适应度值变大的成员,直至没有这样的新成员可以加入.针对节点型社区,Lancichinetti[10]等提出了一种比较典型的适应度函数.
定义2 适应度 对于一个社区S,其适应度为
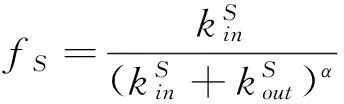
(2)
定义3 节点适应度 社区增加一个新的节点,其适应度fS会发生改变,定义此改变量为该节点的节点适应度,把新加入的节点设为A,其适应度为
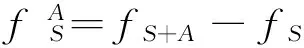
(3)
同理可定义边社区适应度和边适应度.
定义4 边社区适应度 边社区适应度为

(4)
定义5 边适应度 候选邻接边的引入所带来的适应度的变化量
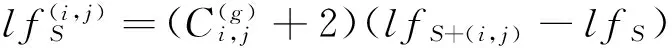
(5)
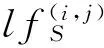
1.3 模块度函数 判断当前社区的邻居节点是否属于边界节点需要引入模块度函数QS[12],该模块度函数基于节点相似性,是对社区划分结果的一种量化.
定义7 节点相似性 在网络G中,若节点i与节点j之间具有连接,则i和j的节点相似性为
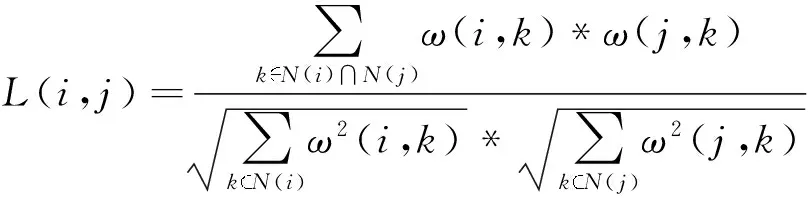
(6)
其中,ω(i,k)表示连接节点i和k的边的权重.本文暂时只考虑非权重网络,所以ω(i,k)=1.
定义8 模块度函数 对于一个网络,模块度为

(7)


(8)
若ΔQS>0,当前社区并入则该边界节点;若ΔQS≤0,则认为v不属于社区C,是C的边界节点.在社区挖掘的过程中引入节点相似性模块度有效地减小了边社区挖掘对于输入参数的不同而带来了差异性,优化了社区挖掘的结果.
1.4 基于边社区的聚合过程以及基于点社区的边界点识别 算法的整体流程如下
步骤1 基于边聚类系数的边排序,并按从大到小的顺序生成队列Q;
步骤2 选取Q中第一条边作为种子边加入到社区C中;
步骤3 从该种子出发不停的聚集新的边到社区,同时更新队列Q;
步骤4 基于模块度函数的边界节点识别;
步骤5 重复迭代步骤3和4,直到社区结构达到完全稳定(步骤5在大部分情况下可以忽略,但是α比较小时,可以采用步骤5来保证社区结构的大小,此时的社区特性更倾向于模块度函数);
步骤6 从Q中选取下一条边作为新的种子,重复步骤3,4和5的过程;
步骤7 直到所有的边都被分配到社区中为止.
第一部分是对边的排序,排序算法的时间复杂度通常都为O(m log2m),m为整个网络的边的数量.第二部分是构建局部社区,时间复杂度为O(e2),e是构成局部社区边的数量,而构建整个网络的社区结构则是第二部分的重复.从整个算法的角度考虑,时间复杂度为O(m log2m+c*e2),其中c为整个网络的社区个数.最极端的情况是整个网络是一个社区,此情况下的时间复杂度为O(m2).针对于绝大部分的真实网络,极端情况一般不会出现.
2 实验与结果分析
采用虚拟网络和真实网络在特征网络上进行测试,并与不同方法比较.实验环境是一台Lenovo PC Intel(R) CPU:Core(TM) i3 550 @3.20 GHz,内存:2 Gi MB,操作系统:Microsoft Windows 7 64位,程序环境:Java 1.8.0_45.
2.1 评价指标 很多社区挖掘算法的过程其实就是一个聚类的过程,因此针对聚类算法的评价在很大程度上可以应用到对社区挖掘算法的评价.
聚类纯度(Purity)作为评价聚类效果的指标之一,可以说是最为简单和直观,其计算公式如下

(9)
其中,X是聚类结果中节点所构成的集合,Y是标准答案所构成的集合.聚类纯度反映了被正确划分的节点数量和所有节点数量的比值,经过归一化的处理,取值范围是0~1,反映了聚类结果和标准答案的相似程度越来越大直至完全相同.
在聚类纯度的定义中,N=|X|.若令N=|Y|,结算结果称为查全率(recall).聚类纯度反映的是节点集中有多少是被正确划分,查全率则反映标准数据集中有多少被正确划分.
F-measure是两者的调和指标
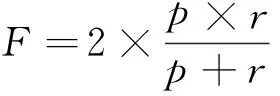
(10)
本文实验部分采用聚类纯度,查全率和调和指标3个指标作为对结果的验证.
2.2 计算机生成网络 基于Newman模型的测试数据集GN-benchmark[13]包含128 个节点,有4个规模一样社区,网络中节点的平均度数K=16.Zin表示节点的内部度,Zout表示节点的外部度,所有边Zout+Zin的平均值是16.针对任何一条边,其存在于某个社区内部的概率Pin=Zin/( Zout+Zin),存在于2个社区之间的概率Pout=Zout/(Zout+Zin).
GN-benchmark应用极为广泛,许多社区挖掘算法都会通过GN-benchmark验证效率和精确度.
随着Zout的增大,Newman-benchmark的社区结构越来越不明显,本文算法在GN-benchmark(Zout=3)时依然有良好的结果.
2.3 真实网络 表1是实验所用到的真实网络的基本数据[14-15],采用的真实网络广泛用于社区挖掘算法的测试.

表1 真实属性数据的测试网络
以美国高校橄榄球联赛网和美国政治博客网为例,分别运用本文算法进行社区挖掘,求得聚类纯度p,查全率r以及调和指标F的各项数值.对比其他3种算法,图1和图2是各算法的在评价指标上的表现.综合3种指标可以发现:文献[3]和文献[16]的算法在聚类纯度和查全率相差比较大;文献[5]的算法聚类纯度和调和指标2项指标差距不大,但查全率较低.本文算法则同时具有较高的聚类纯度和查全率,从而使得F值在维持在较高水平.此外,针对2个数据集的划分结果都达到了很好的模块度值,分别为0.371和0.389.实验结果证明了本文算法在社区挖掘上的准确性和有效性.
综合针对计算机生成网络和真实网络数据集的实验可以得出:针对不同的数据集,边适应度和节点相似性的社区挖掘算法在聚类纯度、查全率方面相比其它算法都有一定程度的提高.尽管无法在聚类纯度、查全率2项评价指标上同时达到最优,但是在结果中,这2项评价指标都维持在较高水平,在整体上体现出了优势,表2中的综合调和指标也充分验证了此结论.
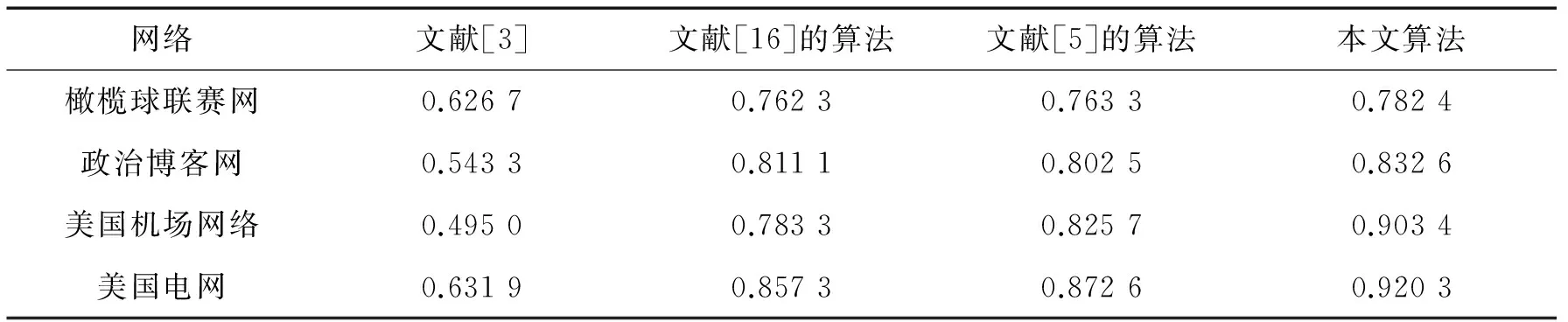
表2 4种算法中的适应度函数值

3 结束语
结合点社区和边社区的优点提出了基于边适应度和点相似性的挖掘算法, 通过网络中的局部信息展开社区挖掘,并以边界节点识别达到控制社区规模和范围的目的,从而解决已有方法对初始节点敏感,终止条件难以获得等问题.在计算机生成网络和真实网络分布进行实验,对实验结果的分析证明了针对不同的网络环境,本文提出的基于边界节点识别的社区挖掘算法具有较高的稳定性和准确率,能够较为真实的对网络的社区结构进行分析.如何将社区挖掘算法进一步应用于大规模的含权网络以及动态明序网络,将是下一步学习研究工作的重点.
[1] Goltsev A V, Dorogovtsev S N, Oliveira J G, et al. Localization and spreading of diseases in complex networks[J]. Physical Review Letters, 2012, 109(12):2 733-2 737.
[2] Xie J, Szymanski B K. LabelRank: A stabilized label propagation algorithm for community detection in networks: proceedings of the Network Science Workshop (NSW) 2013,West Point, April 29-May 1, 2013[C].[S.l.]:IEEE,138-143.
[3] Clauset A. Finding local community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 72(2):254-271.
[4] Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 101(9):2 658-2 663.
[5] Chen Q, Wu T T, Fang M. Detecting local community structures in complex networks based on local degree central nodes[J]. Physica A Statistical Mechanics & Its Applications, 2013, 392(3):529-537.
[6] Wu Y J, Huang H, Hao Z F, et al. Local community detection using link similarity[J]. Journal of Computer Science & Technology, 2012, 27(6):1 261-1 268.
[7] Qi X, Tang W, Wu Y, et al. Optimal local community detection in social networks based on density drop of subgraphs[J]. Pattern Recognition Letters, 2014, 36(1):46-53.
[8] Meo P D, Ferrara E, Fiumara G, et al. Mixing local and global information for community detection in large networks[J]. Journal of Computer & System Sciences, 2014, 80(1):72-87.
[9] Newman M E. Modularity and community structure in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(23):8 577-8 582.
[10] Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure of complex networks[J]. New Journal of Physics, 2008, 11(3):19-44.
[11] Lee C, Reid F, Mcdaid A, et al. Detecting highly overlapping community structure by greedy clique expansion: proceeding of the International Conference on Knowledge Discovery and Data Mining, Bellevue, Washington, July 24-28, 2010[C]. [S.l.] :[s.n.], 2010.
[12] Feng Z, Xu X, Yuruk N, et al. A novel similarity-based modularity function for graph partitioning:proceeding of the International Conference on Data Warehousing and Knowledge Discovery, Regensburg, September 3-7, 2007[C]. Heidelberg: Springer, 2007.
[13] Newman M E, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(2):26 113-26 128.
[14] Institute of Web Science and Technologies at the University of Koblenz-Landau. US airports network dataset-KONECT [EB/OL]. (2013-11-08). [2016-02-20]. http://konect.uni-koblenz.de/networks/opsahl-usairport.
[15] Institute of Web Science and Technologies at the University of Koblenz-Landau. US power grid network dataset-KONECT [EB/OL]. (2013-11-08). [2016-02-20]. http://konect.uni-koblenz.de/networks/opsahl-powergrid.
[16] Luo F, Wang J Z, Promislow E. Exploring local community structures in large networks[J]. Web Intelligence & Agent Systems, 2008, 6(4):387-400.
Algorithm for Community Detection in Social Networks
Yang Cheng1, Du Wencai1,2
(1. College of Information Science and Technology, Hainan University, Haikou 570228, China;2. Faculty of International Tourism and Management, City University of Macau, Macau 999078, China)
In our report, a novel algorithm for discovering local communities in networks was proposed, which was based on fitness and point similarity, combined the advantages of point community and edge community, and mininged the edge community structure using local information. According to the specific central principle, an original edge was used as a seed. In order to obtain the community structure the local community, the fitness function was constantly maximized, and was used to obtain a local edge community. The modular degree function based on point similarity was used for the boundary node identification.
social networks; edge fitness; node similarity; communities detecting
2016-03-11
杨成(1988-),男,安徽六安人,海南大学2013级硕士研究生,研究方向:数据挖掘,移动社交网络等,E-mail:bityangc@qq.com
杜文才(1953- ),男,江苏徐州人,博导,教授,研究方向:信息与通信工程,物联网等,E-mail:wencai@hainu.edu.cn
1004-1729(2016)03-0237-06
TP 391
A DOl:10.15886/j.cnki.hdxbzkb.2016.0036

