具有Markov切换的随机Cohen-Grossberg神经网络时滞依赖的指数同步
周阿丽,何秀丽,印凡成
(河海大学 理学院,江苏 南京 210098)
具有Markov切换的随机Cohen-Grossberg神经网络时滞依赖的指数同步
周阿丽,何秀丽,印凡成
(河海大学 理学院,江苏 南京 210098)
基于随机分析理论以及时滞依赖的反馈控制技术,首先运用Lyapunov函数方法和Gronwall不等式,其次给出了具有Markov切换的随机Cohen-Grossberg神经网络时滞依赖的指数同步的充分性判据,此判据解除了传统意义上时滞延迟的可微性以及其导数的有界性的限制,最后通过一个数值模拟实例验证了理论结果的正确性及有效性.
指数同步; Cohen-Grossberg神经网络; Markov切换; 时变时滞延迟
自从Pecora[1]等最初提出耦合混沌系统的同步性以来,基于其在多种领域中的潜在应用价值,混沌神经网络的同步性理论已被广泛应用在创造安全的交流系统、化学和生物系统以及自动化控制等领域.因此,关于神经网络带有噪声或没有噪声的同步性理论也被广泛研究[2-3].Sun等[4]利用LMI方法研究了混沌系统的指数同步问题,Zhou等[5]利用M矩阵方法研究了神经网络的随机同步问题,同时自适应性同步的问题也得到了广泛的研究[6-7].此外,关于神经网络的指数稳定性问题也取得了很多成果[8-10].特别地,关于Cohen-Grossberg(C-G)神经网络系统的指数稳定性和同步性也取得了很大的成就[11-14].但是在现实应用中,神经网络会出现随机故障,导致链接权值或阀值突然被改变,此类问题可通过Markov切换来模拟,其中,Zhu等[12]运用Halandy不等式等对C-G神经网络系统指数同步做了深入研究.笔者受以上研究的启发,将Lyapunov函数方法、随机分析技术与Grownwall不等式方法等相结合给出了具有Markov切换的变时滞随机C-G神经网络的指数同步的充分性判据,同时不再对传统意义上的时滞函数的可微性以及其导数的有界性做要求.
本文首先介绍了具有Markov切换的C-G神经网络的驱动和响应系统以及所需的一些假设和定义,其次通过构造Lyapunov函数并结合Grownwall不等式等技术得到了对于误差系统的指数同步准则,最后通过一个实例及其数值模拟验证了所得结论的有效性和适用性.
1 模型,符号和假设
设{r(t),t≥0}为状态空间S={i=1,2,…,N}的一个连续时间的Markov链,其生成元矩阵∏=(πij)n×n为
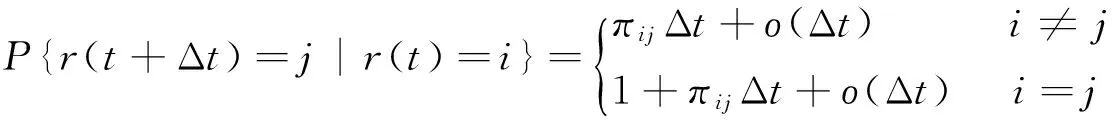
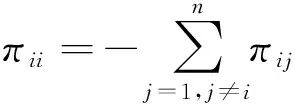
考虑下面的带有时滞依赖的C-G神经网络模型
dx(t)={-α(x(t),r(t))[β(x(t),r(t))-C(r(t))f(x(t))-D(r(t))g(x(t-τ(t)))]+J}dt,
(1)
其中,x(t)=[x1(t),x2(t),…,xn(t)]T是n个神经元的状态向量,α(x(t),r(t))=diag(α1(x1(t),r(t)),…,αn(xn(t),r(t)))代表放大函数β(x(t),r(t))=[β1(x1(t),r(t)),β2(x2(t),r(t)),…,βn(xn(t),r(t))]T为行为函数,C(r(t))=(cij(r(t)))n×n和D(r(t))=(dij(r(t)))n×n分别为连接权矩阵和时滞连接权矩阵. f(x(t))=[f1(x1(t)),f2(x2(t)),…,fn(xn(t))]T和g(x(t))=[g1(x1(t)),g2(x2(t)),…,gn(xn(t))]T为神经元的激励函数,J=[J1,J2,…,Jn]T代表一个恒定的外部输入变量,时滞依赖τ(t)满足0≤τ(t)≤τ,其中τ是一个正常量.
模型(1)为驱动系统,其响应系统为
dy(t)= {-α(y(t),r(t))[β(y(t),r(t))-C(r(t))f(y(t))-D(r(t))g(y(t-τ(t)))]+
J+u(t,r(t))}dt+σ(t,r(t),y(t)-x(t),y(t-τ(t))-x(t-τ(t)))dw(t) ,
(2)
其中,u(t,r(t))表示控制输入向量,w(t)是一个m维布朗运动,假设Markov链r(·)独立于布朗运动w(·),且取u(t,r(t))=K1(r(t))[f(y(t)-x(t))]+K2(r(t))[g(y(t-τ))-g(x(t-τ(t)))],K1(r(t)),K2(r(t))为增益矩阵.
令e(t)=y(t)-x(t)为同步误差,且A(r(t))=C(r(t))+K1(r(t))=(aij(r(t)))n×n,B(r(t))=D(r(t))+K2(r(t))=(bij(r(t)))n×n,则系统(1)和系统(2)误差系统可以表示为
de(t)= {-[α(y(t),r(t))β(y(t),r(t))-α(x(t),r(t))β(x(t),r(t))]+α(y(t),r(t))A(r(t))×
[f(y(t))-f(x(t))]+α(y(t),r(t))B(r(t))[g(y(t-τ(t))-g(x(t-τ(t))]+
[α(y(t),r(t))-α(x(t),r(t))]×[C(r(t))f(x(t)+D(r(t))g(x(t-τ(t)))]}dt+
σ(t,r(t),e(t),e(t-τ(t)))dw(t).
(3)

LV(t,i,e(t))= Vt(t,i,e(t))+Ve(t,i,e(t))·F(t,i,e(t),e(t-τ(t)))+1/2trace[σT(t,i,e(t),

(4)
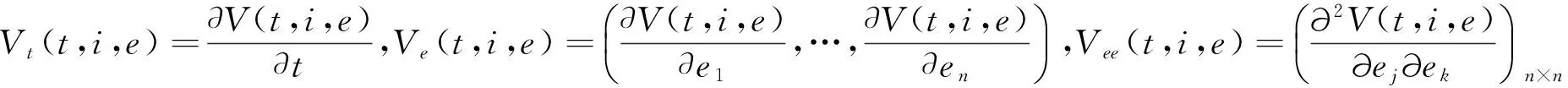
为了得到本文主要结果,给出以下假设:




5) f(0)≡0,g(0)≡0,σ(t,0,0)≡0.
定义1 如果存在正常数γ,λ对于t≥0有E|u(t)-v(t)|2≤γE|u(0)-v(0)|2e-λt,则称2个耦合的神经网络系统(1)和(2)为指数同步的.
2 主要结论

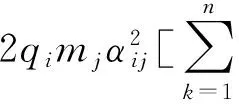
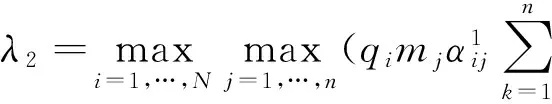
δ1|e(t)|2≤V(t,i,e(t))≤δ2|e(t)|2
(5)以及不等数τ<τ*成立,其中τ*=(δ2/λ1)log(λ1δ1/λ2δ2),则系统(1)和系统(2)是时滞依赖指数同步的.

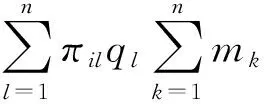
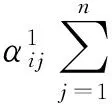
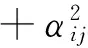
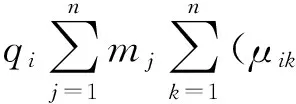
(6)
由假设(1)可得
|ej(t)‖fk(yk(t))-fk(xk(t))|≤u1k|ej(t)‖ek(t)|≤u1k(|ej(t)|2+|ek(t)|2)/2,
|ej(t)‖gk(yk(t-τ(t)))- gk(xk(t-τ(t)))|≤u2k|ej(t)‖ek(t-τ(t))|≤
u2k(|ej(t)|2+|ek(t-τ(t))|2)/2,
(7)
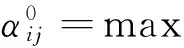
将式(7)代入式(6)并整理可得
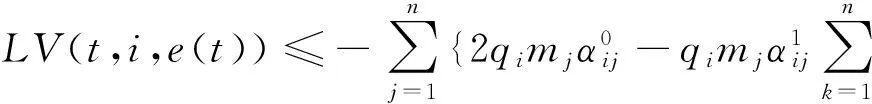
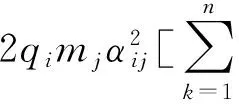

λ1|e(t)|2+|eτ(t)|2,
(8)
另由定理条件可得
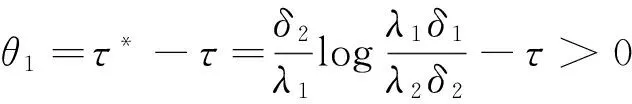
(9)
对于任意t≥τ,存在整数K>2使得(K-1)τ≤t≤Kτ.
定义Lyapunove 函数V1(tm,r(tm),e,eτ),
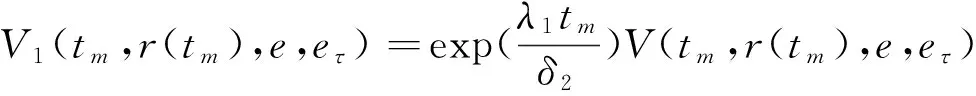
对于0≤m≤K-1,tm=t-mτ.
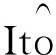
又

由式(5)和(8)条件可以得到

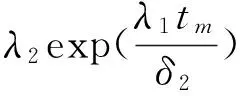
因此
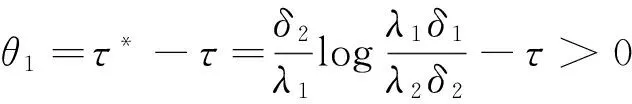

由上述条件可得

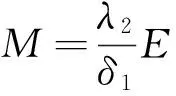
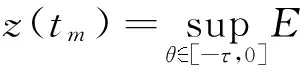
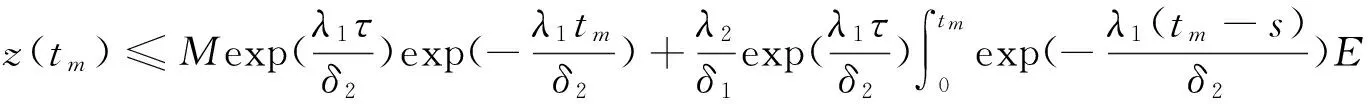


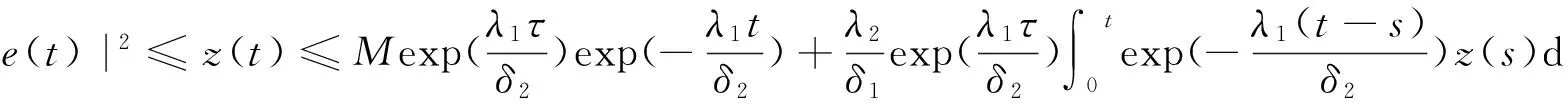
由Gronwall不等式可得
即

因此,由定义可以得出系统(1)和(2)是时滞依赖指数同步的.
注:本文所研究的为时滞依赖的神经网络模型,同时不再对传统意义上时滞函数的可微性以及其导数的有界性做要求.例如文献[11]要求时滞函数可微且其导函数小于1,而本文定理的条件只需时滞函数有界.另外,本文所考虑的激励函数弱化了传统的Lipschitz 条件[4]及函数的单调性及连续可微性[7].
3 数值模拟
将给出具体例子来说明所得结论的有效性和可行性.
例1 考虑如下二维C-G神经网络模型
dx(t)={-α(x(t),r(t))[β(x(t),r(t))-C(r(t))f(x(t))-D(r(t))g(x(t-τ(t)))]+J}dt,dy(t)= {-α(y(t),r(t))[β(y(t),r(t))-C(r(t))f(y(t))-D(r(t))g(y(t-τ(t)))]+J+u(t)}dt+
σ(t,r(t),y(t)-x(t),y(t-τ(t))-x(t-τ(t)))dw(t),
其中,u(t,r(t))=K1(r(t))[f(y(t))-f(x(t))]+K2(r(t))[g(y(t-τ(t)))-g(x(t-τ(t)))],J=(0,0)T,x(t)=(x1(t),x2(t))T,y(t)=(y1(t),y1(t))T,w(t)是二维布朗运动,r(t)为Markov链,S={1,2},生成元矩阵及其他参数为βj(xj(t),i)=2xj(t)(i,j=1,2),αj(xj(t),i)=0.6+0.2cos(xj(t)),τ(t)=0.1|cos t|+1,f(xj(t))=g(xj(t))=(|xj(t)+1|-|xj(t)-1|)/2,

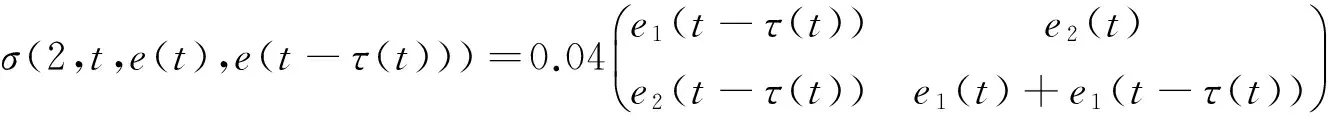
容易验证假设1)~5)成立,其他条件给出如下
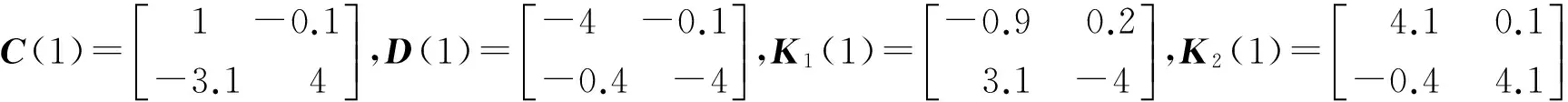
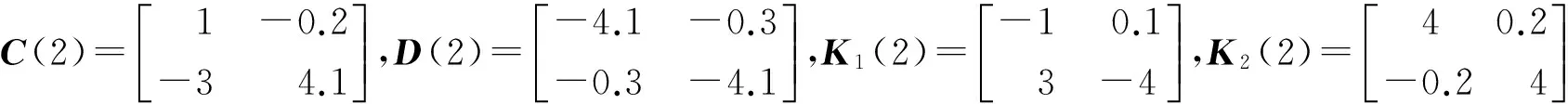
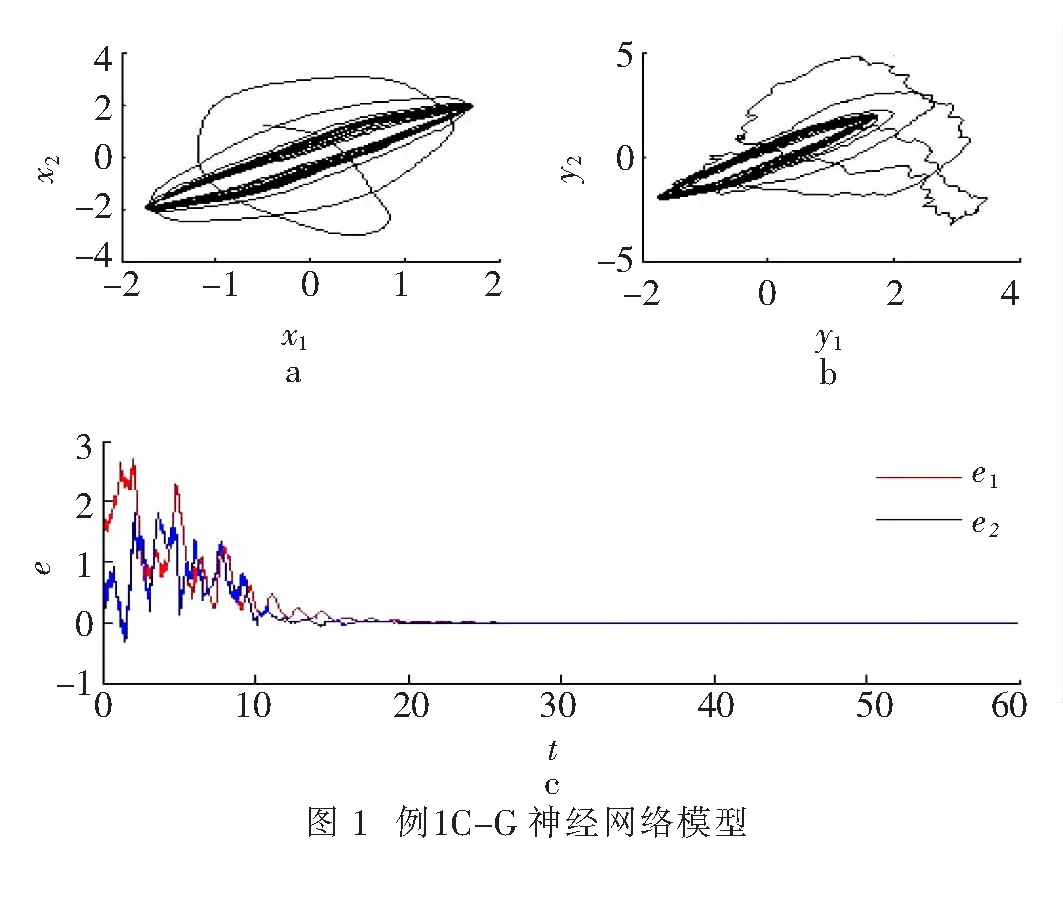
图1 a和b分别显示出系统(1)和系统(2)的混沌现象,取q1=1,q2=0.5,定理中的条件均满足.因此系统(1)和系统(2)是指数同步的,图1 c验证了2个系统的同步性.
4 小 结
研究了具有Markov切换的随机延迟的Cohen-Grossberg神经网络的指数同步问题,基于随机分析理论以及时滞依赖的反馈控制技术,首先运用Lyapunov函数方法和Gronwall不等式,给出了具有Markov切换的变时滞随机Cohen-Grossberg神经网络的指数同步的充分性判据,该判据不在对时滞延迟具有可微性及导数有界性作要求,最后数值模拟实例验证了理论结果的正确性及有效性.
[1] Carroll T L, Pecora L M. Synchronization chaotic circuits [J]. IEEE Trans. Circuits Syst., 1991, 38(4): 453-456.
[2] Li X, Ding C, Zhu Q. Synchronization of stochastic perturbed chaotic neural networks with mixed delays [J]. J. Franklin Inst, 2010, 347(7): 1 266-1 280.
[3] Zhou J, Chen T, Xiang L. Robust synchronization of delayed neural networks based on adaptive control and parameters identification [J]. Chaos Solitons Fractals, 2006, 27(4): 905-913.
[4] Sun Y, Cao J, Wang Z. Exponential synchronization of stochastic perturbed chaotic delayed neural networks [J]. Neurocomputing, 2007, 70(13/15):2 477-2 485.
[5] Zhou X, Zhou W, Yang J, et al. Stochastic synchronization of neural networks with multiple time-varying delays and Markovian jumps [J]. J.Franklin Inst, 2015, 352(3): 1 265-1 283.
[6] Zhang C, Deng F, Peng Y, et al. Adaptive synchronization of Cohen-Grossberg neural network with mixed time-varying delays and stochastic perturbation [J]. Applied Mathematics and Computation, 2015, 269(4): 792-801.
[7] Li X, Cao J. Adaptive synchronization for delayed neural networks with stochastic perturbation [J]. J.Franklin Inst., 2008, 345(7):779-791.
[8] Liu Z, Lü S, Zhong S, et al. pth moment exponential synchronization analysis for a class of stochastic neural networks with mixed delays [J]. Commun Nonlinear Sci Numer Simul, 2010, 15(7): 1 899-1 909.
[9] Zhu Q, Cao J. Stability analysis for stochastic neural networks of neutral type with both Markovian jump parameters and mixed time delays [J]. Neurocomputing, 2010, 73(13/15): 2 671-2 680.
[10] Zhu Q, Cao J. Exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays [J]. IEEE Trans Syst Man Cybern Part B, Cybern , 2011, 41(2) : 341-353.
[11] Zhu Q, Cao J. Exponential input-to-state stability of stochastic Cohen-Grossberg neural networks with mixed delays [J].Nonlinear Dyn, 2015,79(2):1 085-1 098.
[12] Zhu Q, Cao J. pth moment exponential synchronization for stochastic delayed Cohen-Grossberg neural networks with Markovian switching [J]. Nonlinear Dyn, 2012,67(1):829-845.
[13] Zhu Q, Cao J. Exponential stability analysis of stochastic reaction-diffusion Cohen-Grossberg neural networks with mixed delays [J]. Neurocomputing, 2011,74(17):3 084-3 091.
[14] Zhu Q, Cao J. Robust exponential stability of Markovian jump impulsive stochastic Cohen-Grossberg neural networks with mixed time delays [J], IEEE Trans On Neural Networks, 2010, 21(8):1 314-1 325.
[15] 胡适耕.随机微分方程[M].北京:科学教育出版社, 2008.
Exponential Synchronization of Cohen-Grossberg Neural Networks with Time-varying Delays and Markovian Switching
Zhou Ali, He Xiuli,Yin Fancheng
(College of Science, Hohai University, Nanjing 210098, China)
Based on the stochastic analysis theory and delay-dependent feedback control technique, the Lyapunov function and Gronwall inequality were used, and the sufficient criteria of the exponential synchronization of random Cohen-Grossberg neural network time-delay dependent with Markov change was proposed, which removed the differentiability of the time varying delay and the boundness of its derivative. Lastly, a numerical example and its simulation were proposed to demonstrate the effectiveness and correctness of the theoretical results.
exponential synchronization; Markovian switching; time-varying delay; Cohen-Grossberg neural network
2016-03-29
中央高校科研业务费青年教师科研创新能力培育项(A)(2015B19814)
周阿丽(1990-),女,安徽利辛人,河海大学2014级硕士研究生,研究方向:随机神经网络系统稳定性和同步性分析,E-mail:zhoualiahut@126.com
1004-1729(2016)03-0203-06
O 175
A DOl:10.15886/j.cnki.hdxbzkb.2016.0031

