广义生成函数张量分解的欠定混合盲辨识

周志文,黄高明,高 俊

(海军工程大学电子工程学院,湖北武汉 430033)

广义生成函数张量分解的欠定混合盲辨识

周志文,黄高明,高 俊

(海军工程大学电子工程学院,湖北武汉 430033)

针对欠定混合盲辨识的问题,提出了一种广义生成函数张量分解的欠定混合盲辨识算法.该算法不再约束源信号具有稀疏特性.首先将观测信号的广义生成函数的导数叠加成三阶张量的形式,并由此可盲估计源信号的数目;然后对三阶张量进行奇异值分解;最后由联合对角化的方法估计出混合矩阵.仿真结果验证了算法的有效性,且在相同噪声环境下与传统方法进行对比,表明该算法在适定和欠定条件下均可获得更优良的混合矩阵估计精度,扩展了适定情况下基于广义生成函数盲辨识算法的应用范围.

欠定盲辨识;广义生成函数;张量分解;联合对角化;稀疏分量分析

在一定的先验知识前提下,盲信号分离(Blind Source Separation,BSS)在未知原信号和混合系统的情况下能够从观测信号中恢复出原始信号,因而被广泛应用于生物工程、语音信号处理及数字通信中.目前许多算法是根据二阶统计量[1]、高阶统计量[2]、非平稳性[3]和稀疏性[4]来实现盲源分离的.欠定盲信号分离解决的是源信号的数目多于观测信号数目的问题,由于估计出的混合矩阵不存在伪逆,因而它较适定和超定的情况更复杂.

解决欠定盲分离和盲辨识的一般思想是寻求源信号在时域(或某种变换域)的稀疏特性.当稀疏性程度不够高或存在交叉项[5]时,尤其是在信号的稀疏域未知前提下,就会制约稀疏分量分析(Sparse Component Analysis,SCA)的效果,这就使得寻求对源信号没有稀疏性要求的算法尤为重要.当源信号非稀疏但满足相互独立时,利用某些数据结构(如累积量、相关特性或张量采用代数方法)可实现混合矩阵欠定盲辨识[6].假定源信号具有不同的三谱且同符号的峭度非零,文献[7]利用四阶累积量进行欠定盲辨识(FOBIUM),但源信号四阶谱需要具有一定的延时.文献[2]将时间相关的源信号的空间协方差矩阵叠加成三阶张量来解决欠定盲辨识[2].文献[8]利用方法把特征函数的导数张成P阶张量进行分解,从而估计混合矩阵,但需要对原始数据迭代且噪声鲁棒性差.文献[9]将四阶协方差矩阵构成张量形式并利用平行因子分解的方法实现混合矩阵的估计,但它要求源信号四阶累积量为非零,而四阶或高阶累积量计算复杂度高且容易出错.当源信号为复数情况时,文献[10]提出利用广义生成函数(Generalized Generating Function,GGF)的导数矩阵来实现适定盲辨识.为满足实际欠定盲辨识需求,引进张量分解的方法,笔者提出了广义生成函数张量分解的欠定混合盲辨识算法(Tensor Decomposition of Generalized Generating Function-based blind identification of underdetermined mixtures,TD-GGF).先将广义生成函数的Hessian矩阵累积成三阶张量的形式,再通过奇异值分解(Singular Value Decomposition,SVD)对张量分解实现混合矩阵的估计.该方法无须假设源信号具有稀疏特性,并且减小了张量分解的复杂度.

1　信号模型与假设

对于欠定线性混叠模型的盲源分离,假设N个传感器接收到M个源信号的混合(M＞N).那么线性混叠后的信号可表示为

其中,A=[a1,…,aM]∈RN×M,为混合矩阵;x(t)=[x1(t),…,xN(t)]T∈RN,为观测信号;s(t)=[s1(t),…,sM(t)]T∈RM,为源信号;n(t)∈RN,为加性噪声.由于采用观测信号广义生成函数的偏导来估计混合矩阵A,为使A理论上是可辨识的,需要对源信号和混合矩阵进行如下假设:

(1)源信号s1(t),…,sM(t)是非高斯并且相互统计独立的;

(2)混合矩阵任意两列是线性独立的,即对任意i≠j,都不存在ai≠λaj.

2　广义生成函数的盲辨识

定义ϕs(τ)为源信号的广义生成函数[10].对于平稳信号,有,其中τ=[τ1,…,τM]T∈CM,为任意处理向量以使得期望值存在;s=[s1,…,sM]T,为源平稳信号.定义广义生成函数φs(τ)=deflnϕs(τ),则利用源信号间的统计独立性,得

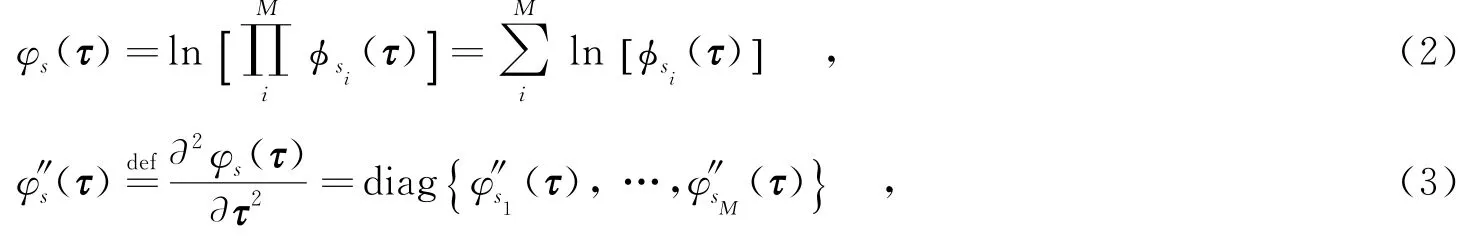
其中,φ″s(τ)为φs(τ)的二阶导数.由前述定义,则可得到观测信号的φx(τ)和φ″x(τ)分别为

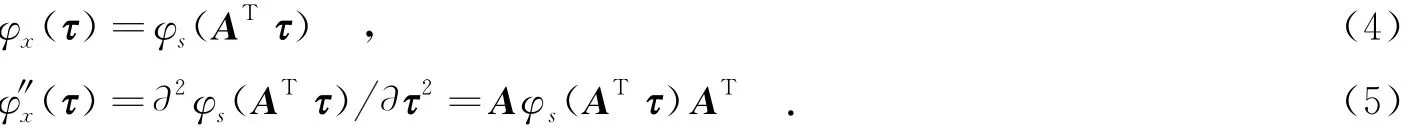
当存在独立加性高斯白噪声,且其协方差矩阵为Gn时,式(5)变为

若Gn已知,通过从φ″x(τ)提取Gn,式(6)退化为无噪的问题.若Gn未知,则对任意处理向量τ,当满足一定条件[11]时,那么通过近似联合对角化(Approximate-Joint Diagonalization,A-JD)可得到混合矩阵的估计.

3　广义生成函数张量分解的盲辨识

然而文献[10]中的算法只适用于适定的情况,即M=N,所以将其扩充为适用欠定的条件具有意义.首先观测信号经过预白化后得到z=Wx,其中W∈RN×N,为白化矩阵.随机选择长度为p的处理向量,即通过观测信号的对数混合密度或者对数混合函数对广义生成函数求其Hessian矩阵Hx.借鉴张量分解的思想,笔者将矩阵Hx叠加成三阶张量,并利用张量分解估计混合矩阵.

对于源信号与观测信号的Hessian矩阵,有

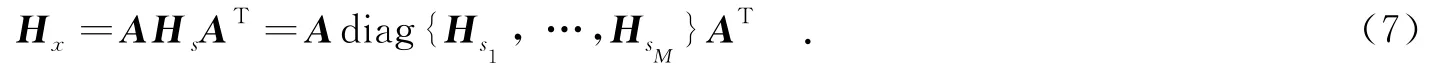
式(7)中观测信号Hx∈RN×K,且K与τ的长度相关.首先定义集合{Cl=Hxl,l=1,…,L},并且L=K/N,那么式(7)可写为

其中,DL为对角阵.将矩阵C1,…,CL累积为张量C∈CN×N×L,且(C)ijl=(Cl)ij,其中1≤i,j≤N,1≤l≤L.定义矩阵D∈CL×M,且(D)lm=(Dl)mm,1≤l≤L,1≤m≤M.那么式(8)可写为

其中,°代表张量外积运算,*为共轭,{am}和{dm}分别为A和D的列向量,因而观测信号的Hessian矩阵就表示为张量的形式.由式(9)可知,三阶张量C被分解为3个秩1向量的外积,并且C的秩是它们线性组合的最小数目[12],因而利用此性质可估计出源信号的数目.目前,盲分离算法一般假设源信号数目已知或者利用一定算法通过估计混合信号矩阵的秩,从而估计出源信号个数,而笔者利用张量分解的同时也盲估计出了源信号的数目.那么由文献[2],可将式(9)写为

其中,☉为Khatri-Rao乘积.对于实信号,若满足M≤min( N(N+1)/2,L),或复信号满足M≤min(N2,L),且A☉A*列满秩时,那么可保证张量分解的惟一性[2].利用此性质可以对张量C分解盲辨识混合矩阵.与文献[11]中的方法不同的是,笔者对三阶张量C进行奇异值分解,C可写为

为求解F-1,下面定义映射:

其中,pijkl=xijykl+yijxkl-xilykj-yilxkj.当且仅当X∈CN×N的秩最大为1时,Ω(X,X)=0.

对于矩阵{Hm}构造的张量集,Λ为任意对角矩阵,使得M=FΛFT,M∈CM×M.利用映射Ω的双线性且秩1特性,可得,这意味着可找到矩阵M并通过一致性联合对角化张量集{Pst}求得F.假定张量是线性独立的,1≤u＜v≤M,那么存在M个线性独立的对称矩阵Mm∈CM×M,满足

矩阵F通过一致性可联合对角化{Mm},即有

其中,{Λi∈CM×M,i=1,…,M},为对角阵,从而可通过式(13)和式(14)找到F.在实际中,考虑到噪声估计的影响,因而式(13)只是近似满足.由于Mm的对称性和Hst=Hts,式(13)可写成

4　仿真实验

为评估笔者提出的广义生成函数欠定混合盲辨识算法的性能,利用相对估计误差EA来衡量混合矩阵的准确性.其定义为[2]

信号采样率为4 k Hz,采样点数为40 000.在本仿真实验中,假定源信号个数为4,在欠定情况下接收通道为3.为衡量笔者提出算法的有效性并与其他盲辨识算法性能对比,仿真实验分别从适定与欠定两种情况来分析.

4.1适定情况

本实验中随机产生4×4的混合矩阵.在信噪比0～20 dB变化范围内,每次进行1 000次蒙特卡罗仿真,并计算混合矩阵的平均相对估计误差,以此来衡量算法的估计精度.在相同条件下分别对比基于二阶统计量欠定盲辨识(SOBIUM)、基于四阶累积量欠定盲辨识(FOBIUM)以及笔者提出的TD-GGF算法,仿真结果如图1所示.由图可以看出,随着信噪比的提高,3种算法盲估计混合矩阵的精度越来越高,验证了提出的算法在适定条件下的有效性.在相同的信噪比条件下,笔者提出的算法估计的精度优于FOBIUM和SOBIUM算法,但性能和FOBIUM相差不大,约1 d B.

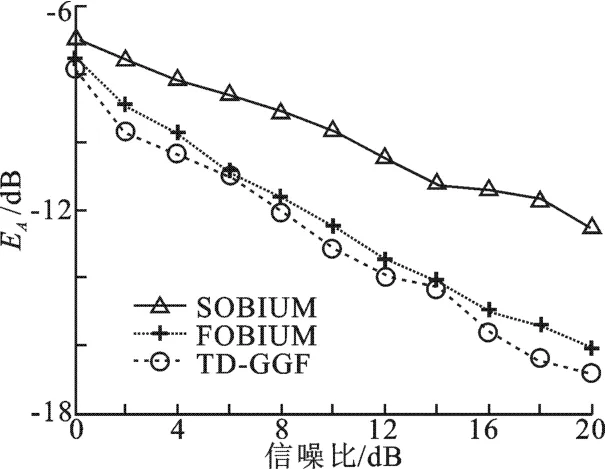
图1　适定情况下混合矩阵的平均相对估计误差

图2　欠定情况下混合矩阵的平均相对估计误差

4.2欠定情况

在与前述相同的源信号前提下,随机产生4×3的混合矩阵.与4.1节相同,在信噪比0～20 d B变化范围内,每次进行1 000次蒙特卡罗仿真,并计算混合矩阵的平均相对估计误差.如图2所示,同样地随着信噪比逐渐增加,算法的估计精度都有一定的提高,且笔者提出的TD-GGF能够获得较好的平均估计误差.尽管在适定和欠定的条件下,笔者的算法与FOBIUM算法性能差异不大,但由于无须计算四阶累积量,避免了大量运算,降低了计算复杂度.同时需要注意的是,无论是文献[10]算法还是笔者提出的欠定盲辨识TDGGF算法,都依赖于处理向量点数和适当的选择,因而在实际应用中还需要对处理向量加以约束,使之更好地满足需求.

5　总 结

目前解决欠定盲辨识的问题广泛采用基于稀疏分量分析的方法,它要求源信号在时域或变换域有稀疏特性.针对源信号为非稀疏的欠定盲辨识问题,笔者提出了一种广义生成函数张量分解的欠定混合盲辨识的算法.仿真结果表明,在适定和欠定的情况下,笔者提出的算法都具有较好的估计精度,因而增大了基于广义生成函数适定盲辨识的适用范围,并且实现简单.但同适定的算法相同,都要寻找合适的处理向量,这是下一步需要研究的方向.

[1]YU C P,ZHANG C S,XIE L H.Blind Identification of Multi-channel ARMA Models Based on Second-order Statistics [J].IEEE Transactions on Signal Processing,2012,60(8):4415-4420.

[2]de LATHAUWER L,CASTAING J.Blind Identification of Underdetermined Mixtures by Simultaneous Matrix Diagonalization[J].IEEE Transactions on Signal Processing,2008,56(3):1096-1105.

[3]YILMAZ O,RICKARD S.Blind Separation of Speech Mixtures via Time-frequency Masking[J].IEEE Transactions on Signal Processing,2004,52(7):1830-1847.

[4]MOHAMED A L,MOHAMED S N,MOHAMED R B.A New Sparse Source Separation-based Classification Approach [J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(11):6924-6936.

[5]纪建,李晓.一种剪切波域的稀疏分量分析方法[J].西安电子科技大学学报,2014,41(1):45-52. JI Jian,LI Xiao.Method for Sparse Component Analysis in the Shearlet Domain[J].Journal of Xidian University,2014,41(1):45-52.

[6]GILLES C,MARTIN K,ERIC M,et al.Joint Matrices Decompositions and Blind Source Separation:a Survey of Method,Identification and Applications[J].IEEE Signal Processing Magazine,2014,31(3):34-43.

[7]FERRÉOL A,ALBERA L,CHEVALIER P.Fourth-order Blind Identification of Underdetermined Mixtures of Sources (FOBIUM)[J].IEEE Transactions on Signal Processing,2005,53(5):1640-1653.

[8]LUCIANI X,de ALMEIDA A L F,COMMON P.Blind Identification of Underdetermined Mixtures Based on the Characteristic Function:the Complex Case[J].IEEE Transactions on Signal Processing,2011,59(2):540-553.

[9]禹华钢,黄高明,高俊.基于JADE和平行因子分解的欠定混合盲辨识算法[J].信号处理,2011,27(8):1189-1194. YU Huagang,HUANG Gaoming,GAO Jun.Algorithm for Blind Identification of Underdetermined Mixtures Based on JADE and Parallel Factor Decomposition[J].Signal Processing,2011,27(8):1189-1194.

[10]GU F L,ZHANG H,ZHU D S.Blind Separation of Complex Sources Using Generalized Generating Function[J]. IEEE Signal Processing Letters,2013,20(1):71-74.

[11]EIDINGER E,YEREDOR A.Blind Source Separation via the Second Characteristic Function with Asymptotically Optimal Weighting[C]//Proceedings of 23rd IEEE Convention of Electrical and Electronics Engineers in Israel. Piscataway:IEEE.2004:404-407.

[12]ZHANG M J.A Fixed Point Algorithm for Blind Identification of Underdetermined Mixtures[C]//2010 Chinese Control and Decision Conference.Piscataway:IEEE,2010:2625-2628.

[13]ZHANG M J,YU S M,WEI G,et al.Sequential Blind Identification of Underdetermined Mixtures Using a Novel Deflation Scheme[J].IEEE Transactions on Neural Networks and Learning Systems,2013,24(9):1503-1509.

(编辑:郭 华)

Tensor decomposition of generalized generating function-based blind identification of underdetermined mixtures

ZHOU Zhiwen,HUANG Gaoming,GAO Jun
(College of Electronic Engineering,Naval Univ.of Engineering,Wuhan 430033,China)

Aimed at the problem of underdetermined blind identification,an algorithm based on generalized generating function decomposition is proposed,which no longer imposes sparsity restrictions on source signals. First,the second derivative matrices of the generalized generating function are stacked to the third-order tensor form,from which the number of source signals can be blindly estimated.Then the tensor is decomposed with singular value decomposition,and the mixture matrix is estimated by the joint diagonalization method.Simulation results validate the effectiveness of the proposed algorithm,and show that the proposed algorithm can acquire a better estimation precision than other classical algorithms with the same SNRs in the conditions of well-posed and underdetermined mixtures,meanwhile it extends the field of blind source separation application via the generalized generating function restricted only to the well-posed case.

underdetermined blind identification;general generating function;tensor decomposition;joint diagonalization;sparse component analysis

TN957

A

1001-2400(2016)05-0116-05

10.3969/j.issn.1001-2400.2016.05.021

2015-07-20 网络出版时间:2015-12-10

国家“863”高技术研究发展计划资助项目(2013AAXXXX061)

周志文(1989-),男,海军工程大学博士研究生,E-mail:mini_paper@sina.com.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.042.html