短时脉冲激励下隧道振动响应与模态参数识别

万 灵 ， 谢雄耀

(1.同济大学地下系 上海，200092) (2.同济大学岩土及地下工程教育部重点实验室 上海，200092)



短时脉冲激励下隧道振动响应与模态参数识别

万 灵1,2， 谢雄耀1,2

(1.同济大学地下系 上海，200092) (2.同济大学岩土及地下工程教育部重点实验室 上海，200092)

为了研究短时脉冲激振力下隧道结构振动响应及有效地提取隧道结构的模态特征。首先分析了锤击作用下的不同短时脉冲激振力精度及其频域特性，其次将短时脉冲激振力应用于上海地铁12号某盾构隧道进行了现场动力测试，最后分析了脉冲激振与隧道结构响应之间的传递函数，并结合随机减量、正交多项式法及自回归滑动平均模型法有效地提取隧道结构的模态参数。结果表明：短时脉冲激振力的中低频振动信号在隧道结构中传递特性较好，传递距离较远。隧道结构的模态频率呈现明显低频特征，前10阶模态频率在100 Hz以下。因此，短时脉冲激振力能够很好地应用于隧道动力测试及模态识别，可为基于模态特征的隧道结构损伤识别及健康监测多个研究领域提供有效的支撑和参考依据。

短时脉冲； 激振； 振动响应； 频响函数； 随机减量； 正交多项式法； 自回归滑动平均模型法

引 言

工程结构的模态特征是结构固有特性，从一定程度上来说，结构的模态特征反映了结构的性能状态，通过识别提取工程结构在不同时段的模态特征，用于判定结构性能是否发生刚度和性能退降，进而用于结构损伤诊断与预报，因此在实际工程中，对工程结构进行有效的动力测试，并通过分析测试振动响应信号提取结构的模态特征是研究的重点与难点。

在工程动力测试中，选择何种激振是动力测试与分析的前提条件，短时脉冲激振力具有发挥迅速、灵活、激振设备简单等优点，通过脉冲锤进行锤击便可获得不同特性的短时脉冲激振力，特别适用于夜间停运检修期间的地铁隧道，它不受地铁交通影响。但是短时脉冲存在着激振能量有限的缺点及不能实现实时检测监测，因此它只适用于结构的局部测试。结构局部振动不同于结构的整体振动，引起结构局部振动所需的能量相对较小。一定程度上，工程实际更关注结构局部特性。

国内外不少学者将脉冲激振法引入至结构模态分析研究中。Chatterjee[1]采用脉冲激振法在巴黎国际大学城站至兰蒂伊市火车区间进行了现场动力测试，测试得到了轨道与土体之间耦合的动力特征，及轨道与土体、轨道与周边建筑之间的频响特征。鸿铁等[2]采用脉冲激振和有限元软件分析出结构古建筑结构的固有频率。龙国平等[3]用脉冲锤击法对大型水电站的水轮机导叶部件和电站厂房楼板进行了现场测试，并得到了这类复杂边界条件的大型结构的固有频率。王利恒等[4]研究了用脉冲锤击试验反应最大值监测钢筋混凝土简支桥梁结构损伤程度。周勇军等[5]基于捶击法对一弯连续钢构模型桥进行动力试验及模态分析。赵才友等[6]采用力锤激振法对钢轨进行了频率响应分析，得到钢轨的振动模态。

笔者以上海地铁12号线某盾构隧道为工程背景，将脉冲短时激振力应用于隧道的现场动力测试，分析了脉冲激振与隧道结构响应之间的传递函数，并结合随机减量、正交多项式法及自回归滑动平均模型(auto-regressive and moving average model，简称ARMA)法有效地提取隧道结构的模态参数。笔者首次将短时脉冲激振力应用于隧道动力测试并对其模态特征进行有效地提取与识别，为基于模态特征的隧道结构损伤识别及健康监测多个研究领域具有重要的理论意义和工程应用参考价值。

1 短时脉冲激振系统

短时脉冲激振实施简单，只需要通过脉冲锤进行锤击便可获得不同特性的短时脉冲激振力。首先对脉冲锤头材料的特性进行测试与分析，选取适合隧道结构的锤头材料；其次对激振力信号的测试和分析精度，在保证力信号精度的同时，选择适合隧道结构的合理采样频率与动力特征识别分析方法；最后阐述了脉冲激振在结构振动传递原理与模态识别。动力测试系统设备主要由LC1302脉冲锤、电荷放大器、 CBOOK2001高精度数据采集器、便携式计算机为主的硬件和C_DAS信号采集系统组成。

1.1 锤头动力特性与频率范围

通过在安装不同材料的垫片产生不同的短时脉冲波，其激振的频域范围也不同，图1为不同材料垫片的短时力脉冲波形图。图2为对应的频谱图。

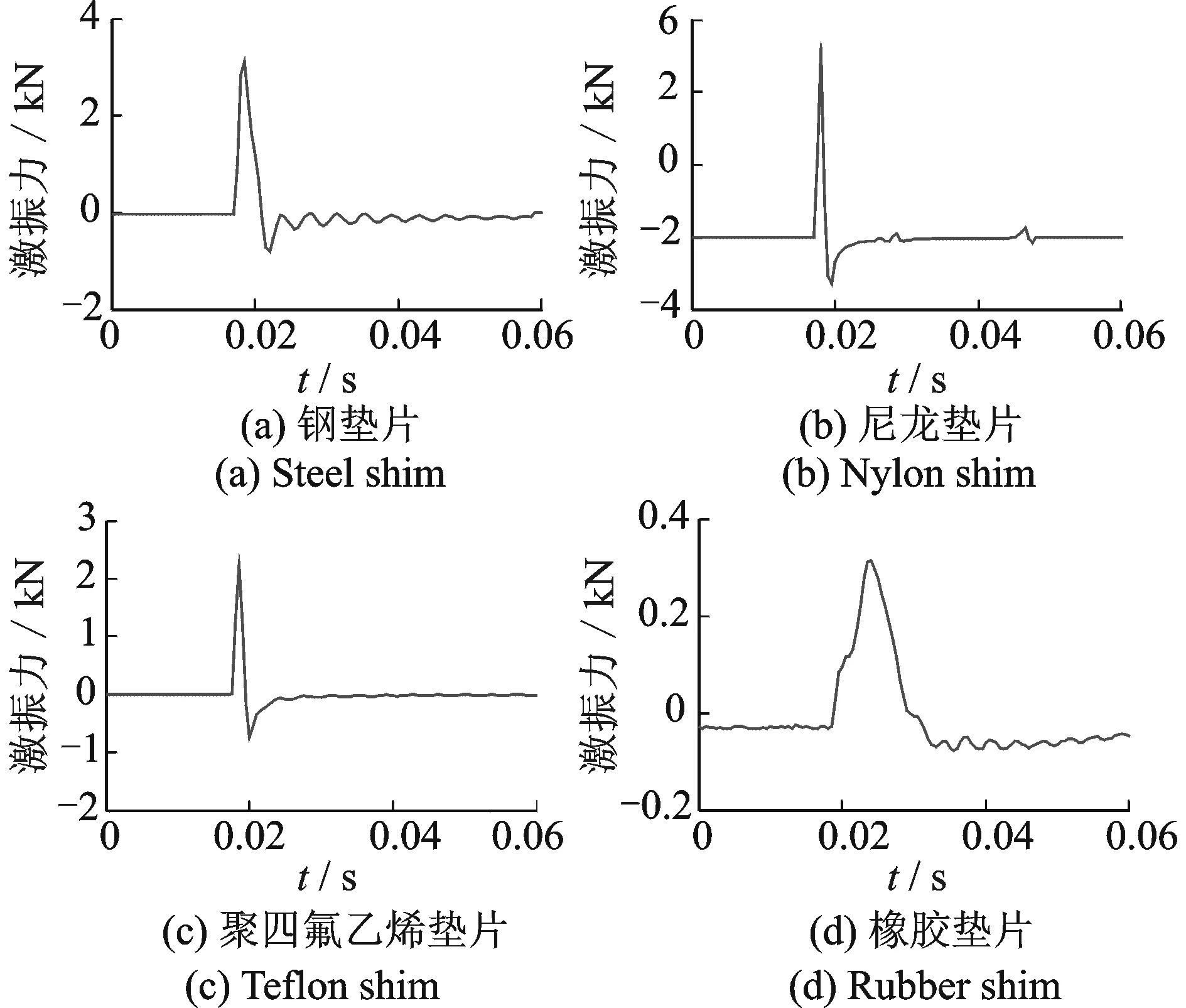
图1 不同垫片短时力脉冲波形图Fig.1 Impulse force signals of different shims

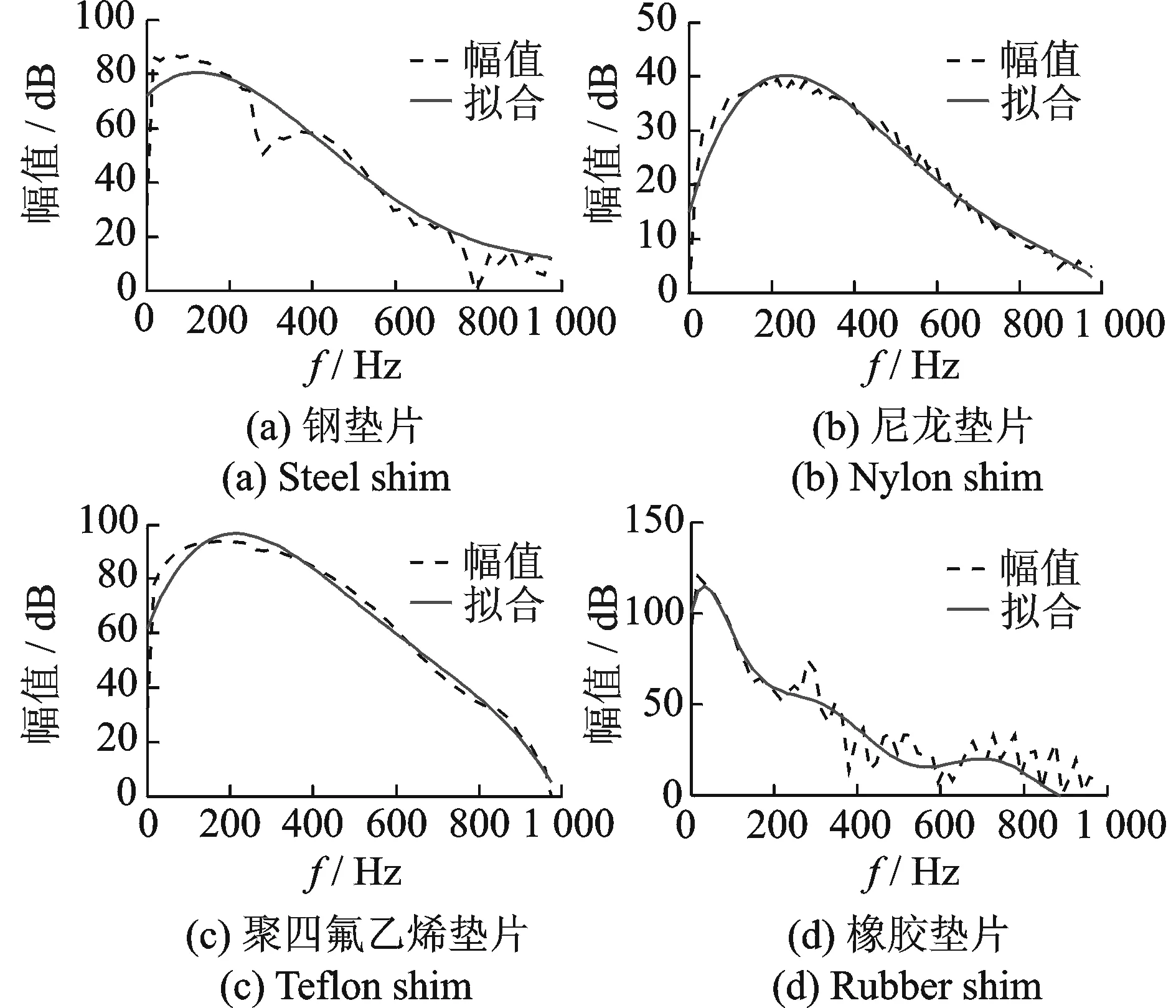
图2 不同垫片短时力脉冲的幅值频谱图Fig.2 Amplitude spectrums of impulse force of different shims

由力脉冲波形图及频谱图可知，锤头材料刚度越大，力脉冲持续时间越短，激振的能量越大，主频范围就越大。由于隧道结构频率呈现出中低频特性,为了更好地激发结构的各阶模态频率，能量耗散应尽可能小一些，因而由选择刚度适中的锤头材料比较适合于地铁隧道的动力测试及动力特性分析，如聚四氟乙烯。

1.2 激振力信号精度分析

在模态测试中采用脉冲锤生成的短时脉冲激励时，尽管可获得较宽频率范围[7],但脉冲激振力作用迅速，持续时间很短，对信号采样离散处理要求较高。当离散数据点数较少时，甚至有时仅能获得1～2个数据点，容易引起测量误差，分析得到的频响函数将不能准确反映结构的动力特征，测试分析的模态精度受到严重影响[8]。因此，为了获得精度较高的激振力，对短时脉冲激振力信号进行精度分析是十分有必要的。

表1给出不同采样时间间隔Δt对信号带来的误差。图3～图4为LC1302脉冲锤产生一个短时脉冲信号的离散精度影响示意图，包括时域波形图和幅值谱图。

工程中，一般采样频率fs要求满足

(1)

其中：fs为采样频率；fmax为信号最高频率；τ为力脉冲的持续时间。

表1 不同采样时间间隔的力信号误差

Tab.1 The force signal errors of different sampling intervals

采样间隔Δt/s力增量Δf/(kN)误差/%τ/2τ/221.46τ/32τ/3sinπ/39.31τ/4τ/4(1+2sinπ/4)5.19τ/5τ/3(1+sinπ/3)2.29

图3 短时脉冲波形时域精度图Fig.3 Accuracy figure of discrete impulse force in time domain

图4 短时脉冲波形频域精度图Fig.4 Accuracy figure of discrete impulse force infrequency domain

如果激振力对应的τ为2 ms，则采样频率应大于2 000 Hz。但对于隧道结构除了大质量、大刚度的衬砌结构之外，还包括隧道壁后土体及其之间相互耦合作用，由于半无限自由空间土体的约束作用，隧道结构呈现低频特性。为了同时满足激振信号的精度和结构低频特性，信号分析中须采用变时基分析得到较精确的结构动力特性[9-11]。

其基本方法是：a.测试中通过设置较高的采样频率来满足短时脉冲激振力的测试精度，保证有足够的采样数据点数；b.增大响应数据分析长度，保证具有足够的时域数据，转换频域分析通过增加傅里叶变换的分析长度来提高频率分辨率；c.选取工程感兴趣的频率范围进行分析，取频响函数的0～fmax频率区间内频率进行截断分析。

1.3 脉冲激振在结构振动传递中的原理与模态识别

通过现场动力测试，分别采用正交多项式法和ARMA来分析隧道结构的模态特征。首先将现场测试原始时程数据进行趋势项、平滑处理预处理；其次采用随机减量法对平滑数据处理得到各个测点的自由振动时程数据和传递函数；最后结合正交多项式和ARMA法对传递函数进行模态特征提取。基于现场动力测试的结构模态特征识别流程图如图5所示。

图5 模态特征识别框图Fig.5 Diagram of the modal identification

目前，在土木结构中使用较多的是位移模态，这种方法也较为成熟。位移模态的基本理论是通过求解结构振动方程，以得到结构的模态参数，如特征频率、阻尼及振型等，其微分方程为

(2)

(3)

其中:φri,φrj为第r阶模态下i，j点的振型；mr为模态质量；ωr为模态频率；ξr为模态阻尼。

动力测试中采用单点激励，多点响应的测试方法。通过测试各点响应值，解耦后为

(4)

其中

(5)

归一化后，即可通过上式识别得到结构的第r阶固有频率ωr及模态振型φri(i=1，…，n)。

2 隧道振动响应分析及模态特征识别

2.1 工程概况

动力测试地点为上海地铁12号线某盾构隧道，盾构隧道直径为6.2 m,单环管片长度为1.2 m。测试中选用聚四氟乙烯锤头，为满足力锤精度，采样频率设为2 000 Hz，在短时脉冲激振下，采集隧道区间不同断面的加速度振动响应信号。加速度拾取点分别沿隧道纵向方向分别布置在162环(N1测点)、158环(N2测点)、154环(N3测点)及150环(N4测点)管片4个断面侧壁处，每个振型响应拾取点间距4.8 m。脉冲激振点在近N1测点处。测点布置示意图及现场测试照片如图6～图7所示。

图6 测点布置示意图Fig.6 Layout sketch of measured points

图7 隧道现场动力测试照片Fig.7 In-site photos of the testing tunnel

本工程动力测试进行了5次激励，对应每次激励的4个脉冲响应，总计20个脉冲响应函数进行分析，并用多参考点正交多项式与自回归滑动平均法进行模态参数识别。识别过程中，使用稳定图方法，以期获得比较准确的模态参数。

2.2 测试数据分析

时程数据是反映结构振动响应特性最直观的数据，将短时脉冲作用下隧道各测点响应信号进行传递函数分析并结合随机减量法、正交多项式法及ARMA法对隧道结构的模态特征进行识别。隧道在一个短时脉冲激振力作用下，隧道各测点振动响应如图8～图9所示。

图8 短时脉冲时程曲线图Fig.8 Time history data of short-time impulse force

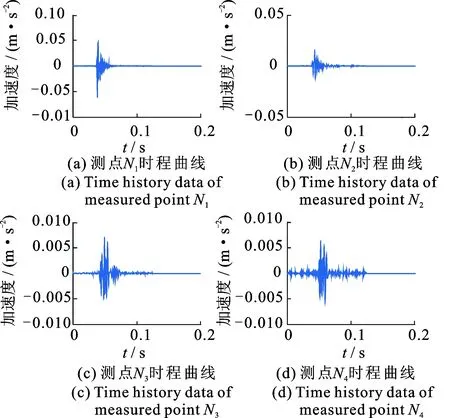
图9 测点响应时程曲线图Fig.9 Time history data of measured points

2.2.1 基于随机减量法的振动响应数据分析

对于平稳随机振动信号，可以认为其平均值为零。在实际振动响应信号中，既包括确定性振动信号，也包括随机信号两类信号，随机减量法就是将确定性信号从随机信号中分离出来，得到自由衰减响应信号，进而为各时域模态参数识别方法提供输入参量。

Cole[13]在1973年最先提出随机减量法，并将其运用于航天飞机结构，并有效地对航天飞机结构的振动模态参数进行了识别。Asmussen等[14]在1999年提出了基于随机减量法的统计理论，之后随机减量法常被用作振动响应数据的预处理方法，分析结构的自由衰减曲线，进而结合其他时域参数识别方法来识别工程结构的模态参数。图10为各个振动响应测点时程数据经随机减量法预处理后的自由振动曲线。

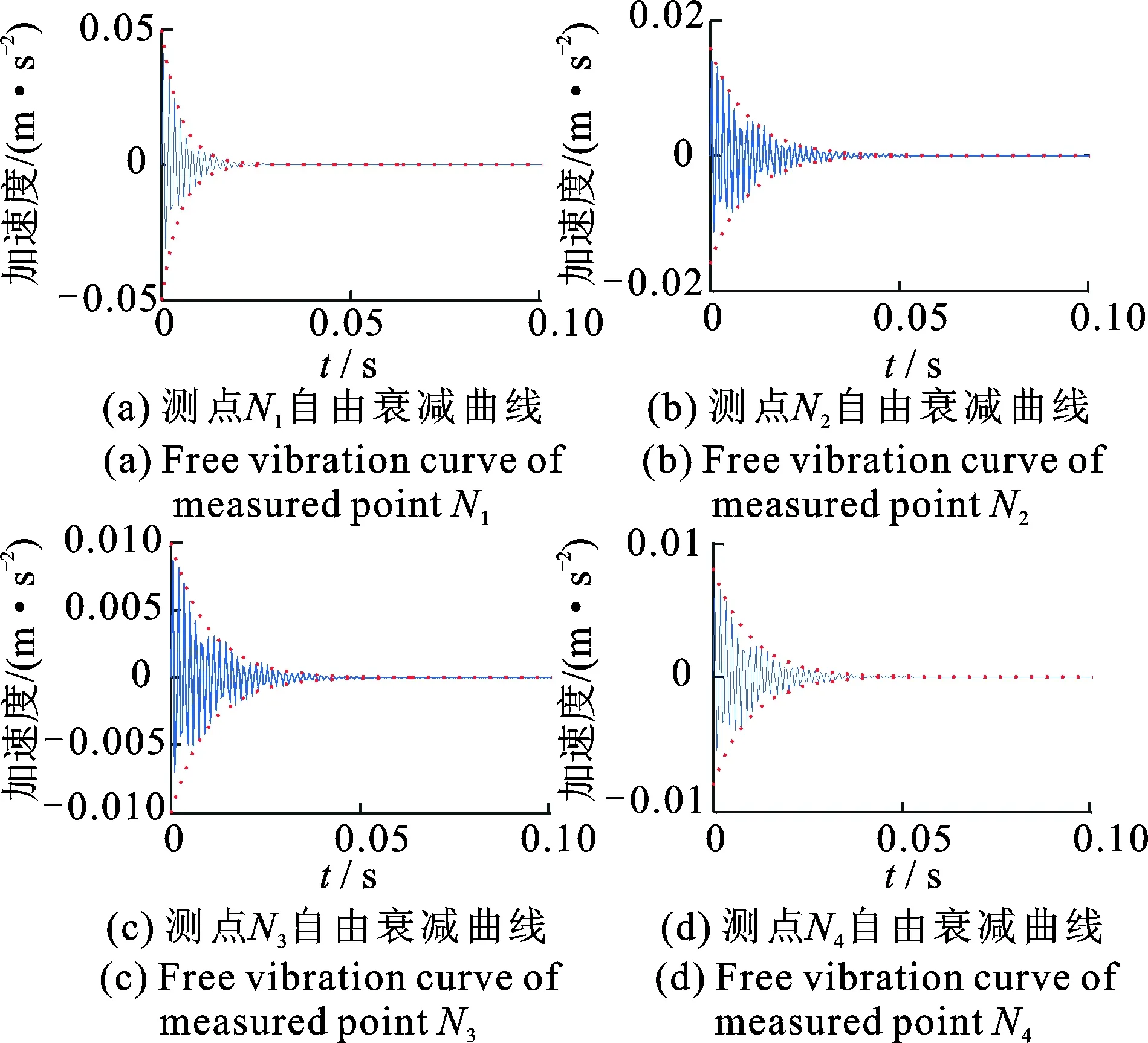
图10 各测点自由振动曲线Fig.10 Free vibration curve of each measured points

将脉冲激励及各个测点响应的随机减量自由振动数据变换至频域内进行分析，且采用变时基采样分析各断面测点的频响函数，可以有效减小谱分析在模态识别中由信号混叠产生的误差，提高模态识别精度。图11为短时脉冲激振下各测点频响函数及相应相位所示。

图11 各测点频响及相位图Fig.11 Frequency response and phase of each measured points

由各测点频响及相位曲线可以看出：

1) 各测点频响、相位具有一致性，在各个频段的频响、相位值基本一致。由此可知，在测试的局部范围内隧道结构的整体性能较好，在实际工程动力测试中，可以优化传感器布置，减少传感器的布置来捕捉隧道结构局部范围内的频域传递特性。

2) 频域范围在0～100 Hz的传递特征较好。在100 Hz以上的传递特性不明显，由此可知，短时脉冲产生的高频振动信号由于介质土体的吸收、耗散，高频信号传递的距离较窄，而低频信号传递的距离较广。由于各个测点的频响特性一致，所以可取一致的频响函数来分析和提取隧道结构的模态特征。

2.2.2 基于正交多项式法的结构模态参数识别

正交多项式算法最早由Richardson等[15]提出，杨毅青等[16]基于正交多项式和稳定图对结构存在密集模态进行参数辨识。

正交多项式所用频响函数的数学模型为

(6)

其中：pi(jω)和qi(jω)为第i阶正交多项式；ci和di为正交多项式系数。

(7)

构造目标函数为

(8)

根据最小二乘法,令

(9)

解得α和β的最小二乘估计。

将上述4个测点与激振的频响函数采用正交多项式法进行模态参数识别，其模态频率稳定图见图12所示。在此稳定图分析中，采用标准定义为：两相邻模型阶次对应的频率值的容许误差为2%，即满足下式即可认为识别值是稳定的。

(10)

在稳定图的基础上选取极点，有效地剔除了多个虚假模态，采用正交多项式识别前10阶模态频率值、均值(fI)及标准差值(fb)，如表2所示。

2.2.3 基于ARMA法的结构模态参数识别

ARMA是通过输入有序随机振动响应数据，进而对工程结构的模态参数进行识别，ARMA是时域参数识别中的常用方法之一。

表2 正交多项式法识别各阶模态频率值

Tab.2 Modal frequencies identified through orthogonal polynomial method Hz

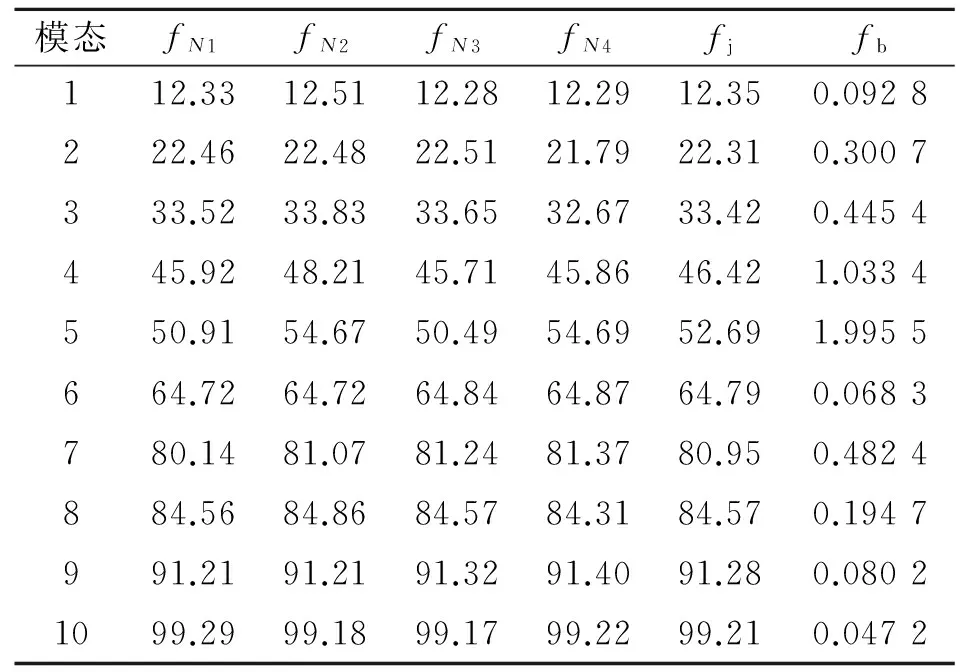
模态fN1fN2fN3fN4fjfb112.3312.5112.2812.2912.350.0928222.4622.4822.5121.7922.310.3007333.5233.8333.6532.6733.420.4454445.9248.2145.7145.8646.421.0334550.9154.6750.4954.6952.691.9955664.7264.7264.8464.8764.790.0683780.1481.0781.2481.3780.950.4824884.5684.8684.5784.3184.570.1947991.2191.2191.3291.4091.280.08021099.2999.1899.1799.2299.210.0472

1969年，Akai[17]首次在对白噪声激励下的结构参数识别中使用了ARMA法。 Kozin[18]于1985年将ARMA法成功、有效地应用于结构的模态参数识别，将结构的随机振动视为白噪声过程并作为结构的输入，采用最大似然估计模态参数。

利用短时脉冲激振力下各个测点振动响应分析得到的传递函数，再结合ARMA进行模态参数识别。图13为单个测点频响函数实部、虚部及ARMA拟合曲线图。

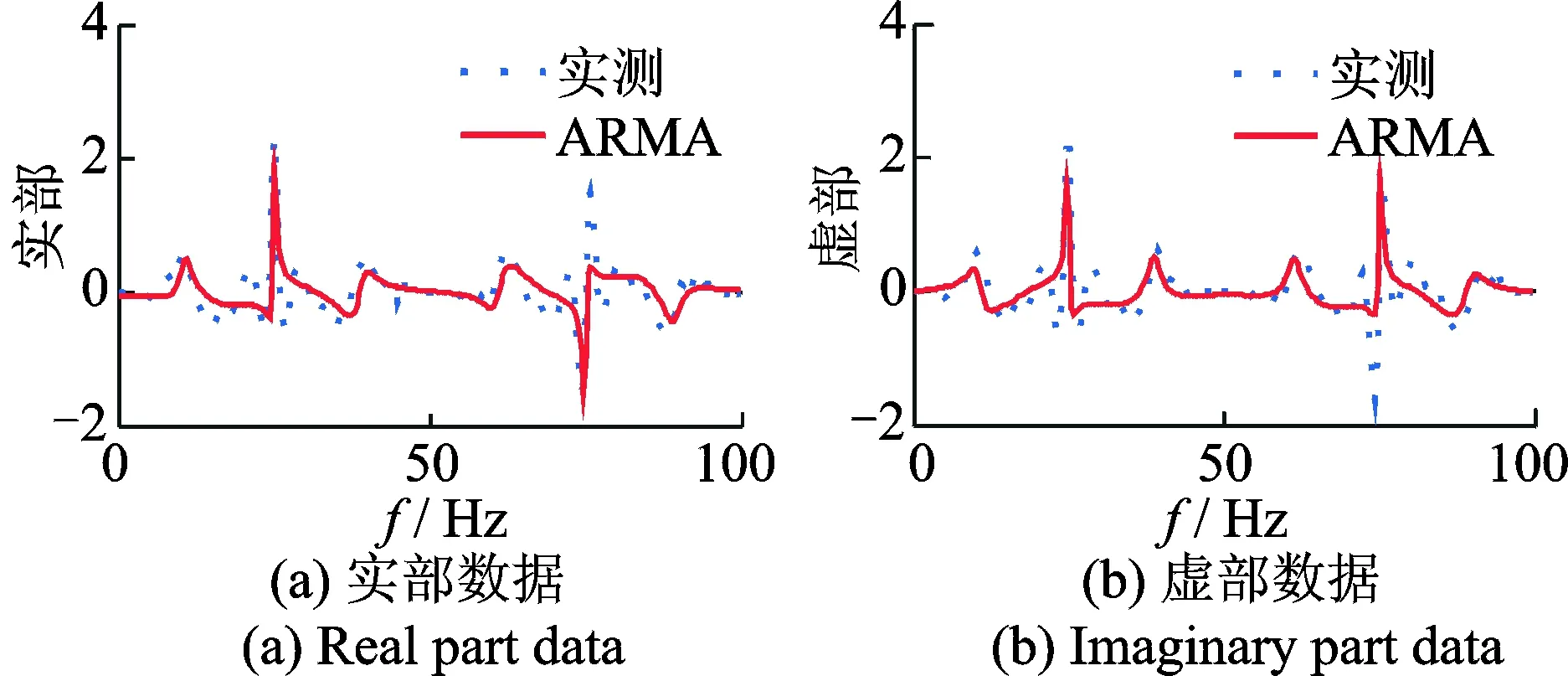
图13 测点频响及ARMA拟合曲线Fig.13 Frequecy responses and ARMA fitting curves of mearsed points

采用ARMA法进行结构模态辨识得到各阶模态频率如表3所示。

由各阶模态频率值可知：

1) 模态频率与模态阶数呈近似线性关系。阶数越高，模态频率值越大；

表3 ARMA法识别各阶模态频率值

Tab.3 Modal frequencies identified through ARMA method

Hz

模态fN1fN2fN3fN4fjfb111.9812.7912.2911.7812.210.3810222.3822.1421.4522.4322.100.3910333.8134.7333.1634.6134.080.6369444.2645.8245.6442.9744.671.1534550.9450.8150.7253.2851.441.0666664.1365.1663.5964.8864.440.6186781.0179.0980.9681.8680.731.0122885.0182.9685.8285.9884.941.2022991.5991.2589.0690.0490.491.00441098.4899.7497.4397.4898.280.9400

2) 隧道结构呈现明显的低频特性，前10阶模态频率值均小于100 Hz。

分析比较在正交多项式法与ARMA法在隧道结构(局部地基梁结构)在纵向方向上的前4阶模态振型如图14所示。

图14 两种方法下的前4阶模态振型图Fig.14 The first fourth order modal shapes of two methods

考虑模态极点及振幅，拟合正交多项式法与ARMA法下的前4阶频响函数(frequency responsefunction,简称FRF)，如图15所示。可以直观看出，两种不同方法下识别的模态参数略有所差异，但整体趋势还是具有一致性，因此认为识别是可靠、有效的。在此基础上，继续分析了在这两种模态识别方法下结构振型的模态置信因子MAC值，如图16所示。

图15 两种方法下低阶FRF拟合图Fig.15 Frequency response function fitting curve of two methods in low order modal

图16 模态置信因子MAC值Fig.16 Value of modal assurance criterion (MAC)

MAC在对角阵上的值均大于0.8，因此，正交多项式法和ARMA法的识别相似度较高，相互验证了识别的有效性。

3 结 论

1) 隧道结构模态频率呈现明显低频特性，前10阶模态频率值均小100 Hz，模态频率与模态阶数呈近似线性关系，模态阻尼与模态阶数呈指数衰减关系。

2) 局部性能较稳定的隧道结构在其局部范围内传递特性具有一致性，可以减少振动传感器布置来捕捉局部频域传递特性。

3) 短时脉冲激振中的低频信号传递范围较广，高频信号能量耗散较快，传递范围较窄。

4) 无论是采用正交多项式法还是ARMA都有效地提取了隧道结构的模态参数。

5) 短时脉冲激振力能够很好地应用于动力测试的隧道结构模态识别，对基于模态特征的隧道结构损伤识别及健康监测多个研究领域具有理论指导和实际应用价值。

[1] Chatterjee P. Experimental results of free field and structural vibrations due to underground railway traffic[C]∥ Proceedings of the Tenth International Congress on Sound and Vibration. Stockholm：Institute of Acoustics，2003:387-394.

[2] 赵鸿铁，张风亮，薛建阳,等. 探讨木结构古建筑结构模型固有频率的几种计算方法[J].西安建筑科技大学学报：自然科学版，2012，44(2)：159-163.

Zhao Hongtie， Zhang Fengliang，Xue Jianyang，et al. Dissussion on the calculation methods of ancient timber structure′s nature frequency[J]. Journal of Xi′an University of Architecture & Technology： Natural Science Edition，2012，44(2)：159-163.(in Chinese)

[3] 龙国平，熊焕庭，毛汉领.用锤击法实测大型工程结构的固有频率[J].广西大学学报：自然科学版，1999，24(2)：148-150.

Long Guoping, Xiong Huanting， Mao Hanling. Measurement of resonant frequencies of large-size engineering structure with hammer hittting[J]. Journal of Guangxi University: Natural Science Edition，1999，24(2)：148-150. (in Chinese)

[4] 王利恒，周锡元，阎维明.用锤击试验反应最大值监测钢筋混凝土简支桥梁结构损伤程度的试验研究[J]. 振动与冲击，2006，25(1)：90-94.

Wang Liheng, Zhou Xiyuan， Yan Weiming. Expermental studies on monitoring reinforced concrete beam′s damage degree using response maxmuns impact excitation vibration test[J]. Journal of Vibration and Shock，2006，25(1)：90-94. (in Chinese)

[5] 周勇军，贺栓海，宋一凡,等.基于锤击法的弯连续钢构模型桥动力试验[J].振动、测试与诊断，2007，27(3)：212-215.

Zhou Yongjun，He Shuanhai，Song Yifan，et al. Dynamic test of curved continuous rigid frame bridge model using hammmer excitation method[J]. Journal of Vibration，Measurement & Diagnosis，2007，27(3)：212-215. (in Chinese)

[6] 赵才友，王平.钢轨-扣件耦联系统的动力特性试验[J].振动、测试与诊断，2014，34(4)：680-683.

Zhao Caiyou， Wang Ping. Experimental study on dynamic characteristics of rail-fastener coupled system. [J]. Journal of Vibration，Measurement & Diagnosis，2014，34(4)：680-683. (in Chinese)

[7] 袁定东,楼和姣,管仁伟.锤击脉冲激振阻抗测试技术提高精度初探[J].振动、测试与诊断，1985(2)：21-26.

Yuan Dingdong, Lou Hejiao， Guan Renwei. The research on the impluse hammer excitation impedance test technology and accuracy improvement[J]. Journal of Vibration，Measurement & Diagnosis，1985(2)：21-26. (in Chinese)

[8] 刘军，高建立，穆桂脂,等.改进锤击法试验模态分析技术的研究[J].振动与冲击，2009，28(3):174-177.

Liu Jun, Gao Jianli， Mu Guizhi， et al. An improved experimental modal analysis system with hammering method[J]. Journal of Vibration ans Shock， 2009，28(3)：174-177. (in Chinese)

[9] 沈松，应怀樵，雷速华,等.用锤击法和变时基技术进行黄河铁路桥的模态试验分析[J].振动工程学报，2000，13(3)：492-495.

Shen Song，Ying Huaiqiao，Lei Suhua, et al. Modal test for yellow river bridge exciting with hammer[J]. Journal of Vibration Engineering, 2000，13(3)：492-495. (in Chinese)

[10]应怀樵.波形和频谱分析与随机数据处理[M]. 北京：铁道出版社，1983：450-456.

[11]Ewins D J. Modal testing: theory and practice[M]. Letchworth: Research Studies Press，1984：35-55.

[12]傅志方.模态分析理论与应用[M].上海：上海交通大学出版社，2000：57-75.

[13]Jr Cole H A. On line failure detection and damping measurement of aerospace structure by random decrement signature[J]. American Institute of Aeronautics and Astronautics Journal，1973，68(1)：288-319.

[14]Asmussen J C，Brincker R, Ibrahim S R. Statistical theory of the vector random decrement technique[J].Journal of Sound and Vibration, 1999，226(2)：329-344.

[15]Richardson M H，Formenti D L. Parameter estimation from frequency response measurements using rational fraction polynomials[C]∥Proceeding of 1st International Modal Analysis Conference. New York：Union College，1982:167-181.

[16]杨毅青，刘强，Munoa J. 基于正交多项式和稳定图的密集模态参数辨识[J]. 振动、测试与诊断，2010，30(4)：429-433.

Yang Y Q，Liu Q，Munoa J. Modal parameter identification of closely-coupled modes based on orthogonal polynomial and stabilization diagram [J]. Journal of Vibration，Measurement & Diagnosis，2010，30(4)：429-433. (in Chinese)

[17]Akaile H. Power spectrum estimation through autoregressive modal fitting[J]. Annals of the Institute of Statistical Mathematics，1969，21(1)：243-247.

[18]Kozin F. Estimation of parameters for system driven by white noise excitation [C]∥Proceedings of International Union of Theoretical and Applied Mechanics Symposium on Random Vibration and Reliability. New York：ASME，1985:163-173.

10.16450/j.cnki.issn.1004-6801.2016.05.027

国家重点基础研究发展计划(“九七三”计划)资助项目(2011CB013803); 上海市科学技术委员会计划资助项目(10231201500，112312000900)

2015-08-27；

2015-11-03

TU93； TH87

万灵，女，1986年12月生，博士生。主要研究方向为隧道结构动力损伤识别。曾发表《Vibration testing and modal analysis of structural system of shield tunnel and soft soil under ambient excitation》(《Proceedings of 6th International Conference on Structural Health Monitoring of Intelligent Infrastructure》，Hong Kong: The Hong Kong Ploytechnic University, 2013)等论文。

E-mail: wanlingstar@126.com