液压柱塞泵压力脉动函数的仿真分析
张天霄
(School of Electrical, Mechanical and Mechatronic Systems, University of Technology Sydney, 2007, Australia)
液压柱塞泵压力脉动函数的仿真分析
张天霄
(School of Electrical, Mechanical and Mechatronic Systems, University of Technology Sydney, 2007, Australia)
流量脉动会引起压力脉动,从而影响液压系统的工作性能,引起结构振动和辐射噪声,会造成液压元件和系统的疲劳破坏,因此仿真分析流量脉动和压力脉动函数对于有效抑制液压柱塞泵的振动和正确设计液压柱塞泵具有重要价值。笔者针对液压泵系统进行定量的振动与噪声分析时所必须具备的激励函数,首先,详细分析了液压泵系统的运行特性,采用傅里叶(Fourier)级数模拟液压泵系统激励函数;然后,建立了压力脉动函数模型;最后,模拟了压力脉动的函数曲线,解决了液压泵系统振动与噪声分析所必需的激励问题。该文为进一步研究液压柱塞泵的定量振动与噪声的响应提供了脉动激励描述,具有理论意义和实际应用价值。
液压柱塞泵; 流量脉动; 压力脉动; 傅里叶级数; 仿真分析
引 言
现代工业对工程质量、产品精度及可靠性都提出了愈来愈高的要求,研究和解决机械工业中出现的各种振动问题已成为一项急迫的任务。如果机械结构系统承受较大的动载荷作用,其振动量将可能超过允许范围的值,会产生强烈的振动和噪声[1-8],从而影响机械设备的工作性能和运行寿命,严重时将会导致机械设备的故障/失效,甚至引起灾难性的事故。液压系统和装置的振动和噪声,不但影响现场工作人员的身心健康,而且会造成设备损坏,降低液压元件和系统的寿命,甚至导致系统和装置的误动作,影响系统的可靠性和安全性,因此降低液压系统的振动和噪声的研究已经成为当务之急的任务。由于液压柱塞泵的复杂性和特殊性,相关柱塞泵的振动特性分析的研究多限于定性的减振降噪试验和分析等[9-15],导致液压柱塞泵定量的振动仿真分析不多见的原因之一,是冲击振动的激励还需要直观和精确描述,只有这样才能研究液压柱塞泵系统的动态特性,并描述系统的历经变化过程。
液压系统和装置的振动激励大体上可以划分为3类:a.周期激励,液压系统和装置随时间周期性变化的激励,可以用Fourier级数描述成为各简谐激励分量;b.渐变激励,液压元件和系统因疲劳、磨损、腐蚀和裂纹等随时间逐渐的变化所产生的激励;c.冲击激励,液压系统在突然启动、停机、变速或换向时,液压阀突然关闭或动作突然停止所形成的瞬时峰值压力。工程实践表明,以上的振动激励均会导致液压系统和装置的故障/失效。众所周知,液压柱塞泵的振动源于激励,而且流量脉动和压力脉动是液压柱塞泵在输送介质过程之中产生振动和噪声的主要根源,因此为了精确设计液压泵和输送管路,必须正确地描述液压柱塞泵的脉动激励,以便准确地解决液压泵振动问题。笔者从液压泵和管路系统流量脉动和压力脉动形成的机理入手,分析流量脉动和压力脉动的传播函数,研究流量脉动和压力脉动的傅里叶级数模拟,从而为抑制和衰减脉动提供理论支撑。
1 流量脉动
为了对液压柱塞泵振动和噪声分析,就要根据液压柱塞泵的结构特点、参数变量、约束情况、运行状况、流量脉动等相关数据和条件,建立液压泵柱塞泵的振动模型,依据研究振动模型的位移、速度和加速度等振动量来衡量振动的强弱,其中主要的因素是振动激励量值。流量脉动是压力脉动的源泉,因此为了研究压力脉动,必须分析流量脉动。
流量脉动是指液压泵在工作时的瞬时流量变化[9-10]。在液压泵连续运转时,多数液压泵形成不断变化的密封容积,各瞬时的流量按一定规律重复变化,会有瞬时非恒定的流量,形成流量脉动。液压柱塞泵的瞬时实际流量可以表示为
(1)
(2)
其中:A为柱塞的横截面积(m2),A=πd2/4;R为柱塞中心分布圆半径(m);d为柱塞直径(m);γ为斜盘倾斜角度(rad);z为柱塞的个数;ω为油缸体转动的角速度(rad/s),ω=2πn/60;n为柱塞泵的转速(r/min);ηV为柱塞泵的容积效率;α为两相邻柱塞间的半夹角(rad),α=π/z;φ为缸体的角位移(rad),φ=ωt。
令
(3)
则有
(4)
(5)
将瞬时实际流量变换为时间t(s)的函数,则有
(6)
(7)
其中:qs1和qs2为柱塞泵的瞬时流量(m3/s)。
显然,当φ=α/2和3α/2(即φ=π/2z和3π/2z)时,瞬时流量达最大值qsmax;当φ=0和α(即φ=0和π/z)时,瞬时流量达最小值qsmin。由此定义的流量脉动系数δq为
(8)
其中:qt为理论平均流量(m3/s)。
轴向柱塞泵的缸体每旋转一周,每个柱塞往复一次,完成一次吸油和压油,因此理论平均流量qt和实际流量q可以表示为
qt=2AznRtanγ=15zωd2Rtanγ
(9)
q=2AznRηVtanγ=15zωd2RηVtanγ
(10)
2 压力脉动
流量脉动必然带来压力脉动,这意味着液压柱塞泵工作执行装置输出的流量与压力随时间变化,可见液压柱塞泵输出的流量与压力并非是绝对稳定的,由于液压柱塞泵容积的变化总会导致输出压力流体的波动,从而产生振动和噪声。根据流体力学基本原理,液压柱塞泵的柱塞和缸体之间封闭腔的流量变化必然引起压力的变化。对于可压缩的液流而言,瞬时实际压力可以表示为
在0≤t≤π/zω内
(11)
在π/zω≤t≤2π/zω内
(12)
其中:Eq为液流弹性模量(Pa)。
单个柱塞封闭腔容积为
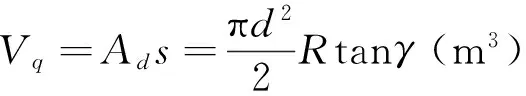
3 傅里叶级数模拟
液压柱塞泵的流量脉动和压力脉动是一种非简谐的周期函数,这种周期函数可以用简谐的傅里叶(Fourier)级数来表示,这样就得到了对应傅里叶级数的简谐激励作用的液压柱塞泵的动态响应问题。
由于液压柱塞泵工作原理的特殊性和流液脉动的复杂性,采用任意区间的傅里叶级数模拟系统激励。将区间为[e1,e2]的周期激励函数F(x)展开为傅里叶级数,即
(13)

式(13)表明,一个复杂的周期激励函数可以分解为一系列简谐函数的叠加。傅里叶级数的系数a0,aj与bj可以由下式确定,即
(14)
(15)
只要定义的aj和bj积分存在,就能够用傅里叶级数来表示函数F(x)。如果F(x)不能以函数表示,可以近似模拟计算。
将式(11-12)表示的周期压力脉动展开为傅里叶级数,其傅里叶级数的系数为
(16)

(17)
(18)
由流量脉动量引起的压力脉动量可以表示为
(19)
其中:ps为柱塞泵的压力脉动量(Pa)。
根据式(19)通过傅里叶级数可以模拟多级压力脉动函数,图1中给出了取j(j=1, 2, …, 10)的压力脉动函数曲线。

图1 压力脉动ps/Pa的变化曲线Fig.1 The change curve of pressure pulsation ps(Pa)
可以认为只要满足相关条件,任何周期函数都可以用简谐收敛的傅里叶级数来描述,相对应的就是简谐激励作用的响应问题。
4 结束语
在液压系统和装置中,由于流量脉动和压力脉动常常沿管路传播,由此引起的振动和噪声将劣化液压系统和装置工作性能、将缩短液压元件和系统的工作寿命、将恶化现场工作环境。因此探讨流量脉动和压力脉动的仿真模拟对于研究液压柱塞泵的振动问题以及进一步探讨振动抑制问题具有积极意义。笔者建立了能够反映液压系统和装置的流量脉动和压力脉动的数学模型,通过傅里叶级数模拟了多级压力脉动函数,为进一步分析液压系统和装置的振动问题打下了坚实的理论基础,为研究液压系统和装置的动态特性提供了实用依据。
[1] Timoshenko S, Young D H, Weaver Jr W. Vibration Problems in Engineering[M]. 4th Edition. New York: John Wiley & Sons, 1974:76-92.
[2] Meirovitch L. Elements of vibration analysis[M]. New York: McGraw-Hill, 1975:59-70.
[3] Thomson W T, Dahleh M D. Theory of Mechanical Vibration with Applications[M]5th Edition. New Jersey: Prentice-Hall, Inc., 1998:89-100.
[4] 郑兆昌. 机械振动[M]. 北京: 机械工业出版社, 1980:98-103.
[5] 季文美, 方同, 陈松淇. 机械振动 [M]. 北京: 科学出版社, 1985: 85-93.
[6] 刘延柱, 陈文良, 陈立群. 振动力学 [M]. 北京: 高等教育出版社, 1998: 42-45.
[7] 张义民. 机械振动 [M].北京: 清华大学出版社, 2007: 50-54.
[8] 屈维德, 唐恒龄. 机械振动手册[M].2版. 北京: 机械工业出版社, 2000: 51-57.
[9] 路甬祥. 液压气动技术手册[M]. 北京: 机械工业出版社, 2002: 470-541.
[10]李壮云. 液压元件与系统[M].2版.北京: 机械工业出版社, 2010: 71-76.
[11]Spence R, Amaral-Teixeira J. Investigation into pressure pulsations in a centrifugal pump using numerical methods supported by industrial tests [J]. Computers & Fluids, 2008, 37(6): 690-704.
[12]Zhang Bin, Xu Bing, Xia Chunlin, et al. Modeling and simulation on axial piston pump based on virtual prototype technology [J]. Chinese Journal of Mechanical Engineering, 2009, 22(1): 84-90.
[13]Xu Bing, Zhang Junhui, Yang Huayong. Simulation research on distribution method of axial piston pump utilizing pressure equalization mechanism [J]. Proceedings of the Institution of Mechanical Engineers Part C—Journal of Mechanical Engineering Science, 2013, 227(C3): 459-469.
[14]诸葛起, 路甬祥. 用振动信号检测柱塞泵松靴故障 [J]. 振动、测试与诊断, 1989, 9(3): 11-15.
Zhuge Qi, Lu Yongxiang. Fault detection of loose slipper with piston pump by vibration signals [J]. Journal of Vibration, Measurement & Diagnosis, 1989, 9(3): 11-15.(in Chinese)
[15]严根华, Fiebig W. 液压泵振动与噪声的分析和控制研究 [J]. 振动、测试与诊断, 1999, 19(4): 350-381.
Yan Genhua, Fiebig W. Analysis and control of vibration and noise in hydraulic static pumps system [J]. Journal of Vibration, Measurement & Diagnosis, 1999, 19(4): 350-381.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.05.004
*国家自然科学基金资助项目(51675216);国家重点基础研究发展计划(“九七三”计划)资助项目(2014CB46303)
2014-07-23;
2015-11-10
TH113.1; TH137.5
张天霄,男,1986年7月生,博士生。主要研究方向为液压传动、可靠性设计和自动控制等。曾发表《Reliability design for impact vibration of hydraulic pressure pipeline systems》(《Chinese Journal of Mechanical Engineering(CJME)》 2013,Vol.26,No.5)等论文。
E-mail:zhangtx11@mails.jlu.edu.cn

