Relative dynamics estimation of non-cooperative spacecraft with unknown orbit elements and inertial tensor

Yu Hn,Zhng Xiujie,Liu Lingyu,Wng Shuo,Song Shenmin

aBeijing Institute of Astronautical Systems Engineering,Beijing 100076,China

bCenter for Control Theory and Guidance Technology,Harbin Institute of Technology,Harbin 150001,China

cAcademy of Fundamental and Interdisciplinary Science,Harbin Institute of Technology,Harbin 150001,China

Relative dynamics estimation of non-cooperative spacecraft with unknown orbit elements and inertial tensor

Yu Hana,b,*,Zhang Xiujiec,Liu Lingyua,Wang Shuob,Song Shenminb

aBeijing Institute of Astronautical Systems Engineering,Beijing 100076,China

bCenter for Control Theory and Guidance Technology,Harbin Institute of Technology,Harbin 150001,China

cAcademy of Fundamental and Interdisciplinary Science,Harbin Institute of Technology,Harbin 150001,China

Cubature Kalman filter;MAP estimator;Non-cooperative spacecraft;Relative motion;Stereo vision

The state estimation for relative motion with respect to non-cooperative spacecraft in rendezvous and docking(RVD)is a challenging problem.In this paper,a completely non-cooperative case is considered,which means that both orbit elements and inertial tensor of target spacecraft are unknown.By formulating the equations of relative translational dynamics in the orbital plane of chaser spacecraft,the issue of unknown orbit elements is solved.And for the problem for unknown inertial tensor,we propose a novel robust estimator named interaction cubature Kalman filter(InCKF)to handle it.The novel filter consists of multiple concurrent CKFs interlacing with a maximum a posteriori(MAP)estimator.The initial estimations provided by the multiple CKFs are used in a Bayesian framework to form description of posteriori probability about inertial tensor and the MAP estimator is applied to giving the optimal estimation.By exploiting special property of spherical-radial(SR)rule,a novel method with respect to approximating the likelihood probability of inertial tensor is presented.In addition,the issue about vision sensor’s location inconformity with center mass of chaser spacecraft is also considered.The performance of this filter is demonstrated by the estimation problem of RVD at the final phase.And the simulation results show that the performance of InCKF is better than that of extended Kalman filter(EKF)and the estimation accuracy of pose and attitude is relatively high even in the completely non-cooperative case.

1.Introduction

Estimation of relative motion between spacecraft has attracted extensive attention in the last few years.1Especially,it is very important in the rendezvous and docking(RVD)research.2RVD is a key technology,which is required for many spacemissions such as assembly in orbit,re-supply of orbital platforms,repair of spacecraft in orbit,etc.3The RVD missions which have been implemented so far include orbital express4,engineering test satellite(ETS)-VII5and automated transfer vehicle(ATV).6However,most of them are treated as cooperative space missions.Namely,relative estimation algorithm depends on information exchange between spacecraft or some type of beacon preassembled in target spacecraft.7,8

In fact,many RVD missions are involved with noncooperative spacecraft,such as enemy satellite,major inorbit satellites,etc.In these missions,the estimation of relative motion turns to be more complicated,as there is a little information about pose and configuration of the target spacecraft.And grappling and anchoring to non-cooperative objects is regarded as the top technical challenge in the demonstration mission of NASA flagship technology.9In Ref.10,noncooperative spacecraft is defined as, ‘‘non-cooperative spacecraft means that there is no communication system or any other active sensor,and thus its orientation cannot be determined by electronic inquiry or signal emission”.

There is little literature that deals with the problem of relative motion estimation about non-cooperative target.Vision-based estimation of relative motion could be a kind of available solutions for the problem of RVD missions at the final phase.Specially,stereovision technique is widely used in the motion estimation.11–15In general,the geometrical characteristic of spacecraft is recognized by vision sensors sampling a sequence of images,such as solar panel,antenna boom,payload attach fitting,nozzle of apogee motor.In Ref.11,it took four natural features placed on the target satellite to determine relative pose in real time.However,its effectiveness for noncooperative target is limited,as it supposes that the positions of feature points on target satellite are previously known.Xu et al.12proposed a method in which solar panel of spacecraft is identified by Hough transform and provided closed-form expressions about position and attitude of spacecraft.More recently,Liu et al.13developed a novel algorithm which is based on information fusion of multi-feature to estimate the pose of non-cooperative satellite.And it takes the contour and nozzle of target satellite as the multi-feature.In addition to the above-mentioned feature-based algorithms,there is another way to determine pose information.In Ref.14,the relative motion was estimated using a distinctive approach which is named algorithm of mode-based pose refinement.Nevertheless,it needs to take advantage of a prior knowledge of target 3D model and its initial pose estimation.Zhou et al.15applied extended Kalman filter(EKF)to estimate the relative states.However,it is not referred to the situation that vision sensor’s location does not coincide with the spacecraft’s center of mass(c.m.).If the above situation is concerned,a novel kinematic coupling between the rotation and translation will exist.16And considerable errors in a rendezvous problem will take place if this perturbation is ignored.

The equations of translational relative dynamics between spacecraft are always resolved in the frame of target spacecraft(e.g.,Clohessy–Wiltshire(C–W)equations).However,it is not suitable for non-cooperative applications since the orbit elements of target spacecraft are unknown.In addition,the inertial tensor of target spacecraft is also unknown.The main purpose of this paper is to design a robust filtering scheme for estimating relative motion status with respect to noncooperative scenarios that both orbit elements and inertial tensor of target spacecraft are unknown.And the issue about unknown inertial tensor is the major consideration in this paper.Actually,this issue can be regarded as a combined estimation problem.In other words,it means that both state variables of system and unknown inertia tensor are estimated simultaneously at the given observations.One approach for combined estimation is to take the scale of unknown inertia tensor as state augmentation.17,18However,it just takes the principal moments of inertia into account and does not directly give the value of inertial tensor.Besides,the increase of dimension of the state vector is likely to cause the estimation inconsistency particularly in the nonlinear dynamic system.Another approach is to design an interactive filter,which is either to estimate the state from the unknown parameters or to estimate the unknown parameters from state.19Nevertheless,the scheme in Ref.19is open-loop and it takes iterated extended Kalman filter(IEKF)which is of low precision and inconsistency for a high-dimensional nonlinear system to estimate state.In this paper,we take the same idea to deal with the problem of the unknown inertia tensor by designing an external estimator interlaced with cubature Kalman filter(CKF).It is proved that CKF is optimal when embedded in the Bayesian filter and its precision and consistency with respect to a highdimensional nonlinear system are better than those of conventional nonlinear filters,20such as EKF,unscented Kalman filter,quadrature Kalman filter,etc.Furthermore,we propose a novel method to estimate the probability density of inertia tensor.As for the issue about the unknown orbit elements of target spacecraft,we take equations resolved in the frame of chaser spacecraft to describe the translational relative dynamics between spacecraft.And the case that vision sensor’s location does not coincide with chaser spacecraft’s c.m.is also considered.

The rest of this paper is organized as follows:Section 2 presents the model of relative dynamics;Section 3 states the problem of RVD for non-cooperative target;Section 4 presents the algorithm of InCKF;Section 5 gives the numerical simulation results and demonstrates the performance of InCKF for pose estimation;Conclusion remarks are drawn in Section 6.

2.Mathematical formulation

Presuppose that two spacecraft are in orbit around the earth.One is the chaser spacecraft with respect to a reference satellite on an eccentric orbit and the other is the target spacecraft in a circular orbit.It is assumed that the chaser spacecraft is equipped with two cameras to capture images ofNfeature points on the target spacecraft.And the positions of feature points on the target spacecraft are unknown.The relative orbital motion of the two spacecrafts is illustrated in Fig.1.

In Fig.1,the following coordinate systems are concerned:FI,the Earth-centered inertial reference frame,whose originalOIis located in the center of the Earth,with the fact that itsXIis pointed to the vernal equinox,itsZIis directed along the rotational axis of the Earth,andYIcomplies with the righthanded rule;FC,a local-vertical and local-horizontal Cartesian reference frame fastened to the chaser spacecraft c.m.,withXCbeing a unit vector directed from the center of the Earth to c.m.,ZCtowards the direction of chaser spacecraft motion in the chaser’s orbital plane,andYCcompleting the dextral triad;FT,a Cartesian right-hand body-fixed reference frame with its originalOTriveting to the target spacecraft’s c.m.In the following article,we premise that the orbital reference frameFCaccords with the body-fixed frame of the chaser spacecraft.RTandRCare the distance from the target and chaser to the Earth,respectively.And the vector between the c.m.of chaser and target,resolved inFC,is denoted by ρ=[x,y,z]T.

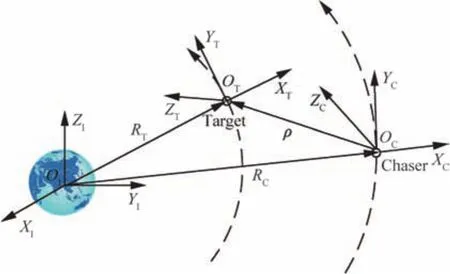
Fig.1 Relative motion of chaser and target.

2.1.Relative translational dynamics

It is considered that the target spacecraft is non-cooperative and the orbit angular velocity of the target spacecraft is unknown.So the conservative relative translational dynamics which projects onto the orbital plane of target spacecraft is invalid.Thus,we formulate equations in the orbital plane of chaser spacecraft to present the relative motion at the final phase of rendezvous and docking as

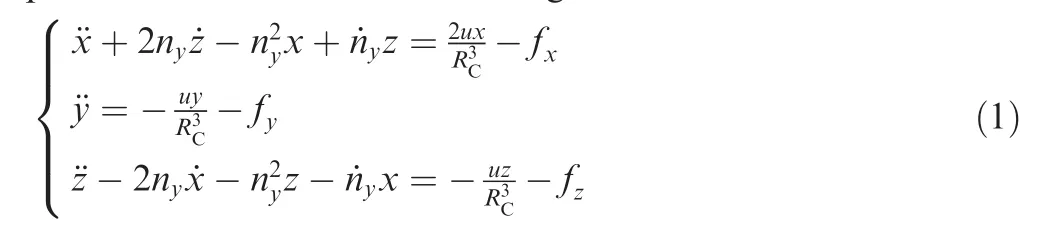
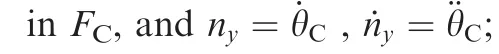
And θCis the true anomaly of the chaser spacecraft

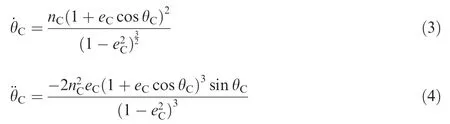
However Eq.(1)just only refers to the relationship of the c.m.of the two spacecraft,which will lead to considerable errors about relative translation when the point is not located in the c.m.of the spacecraft.16Suppose thatPCis a location of the vision sensor in the chaser spacecraft.Then PCis a vector directed fromPCto the origin of the reference frameFC.Piis an arbitrary feature point in the target spacecraft and Piis its corresponding vector directed from the origin of the coordinate systemFTto the pointPi.According to vector addition,it is obvious that the following relationship holds:

where ρ0is a vector from the chaser’s c.m.to the target’s c.m.;ρidenotes the relative position vector between the vision sensor’s location and the feature point with the direction fromPCtoPi.It is straightforward to deduce the first and second time derivatives of Piand ρiinFC,

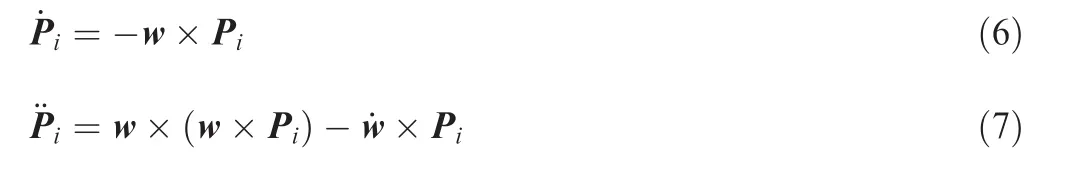
Eqs.(6)and(7)imply that rotation-translation coupling is able to affect the relative translation.In Ref.16,it is treated as a kinematic perturbation.This perturbation effect always exists and it is an inherent part of the spacecraft relative motion nothing to do with external disturbation.Specifically,it is more dominant than orbital perturbations at the final phase of RVD.Furthermore,because the target is noncooperative and the equationsofrelative translational dynamics need to project onto the reference frameFC,the time derivatives of relative position vector are different from those given in Ref.16.

2.2.Relative rotational dynamics

Although quaternion is the most popular approach to represent rigid-body attitude,its four components increase the inconsistent probability of the system to be considered.The Modified Rodrigues parameter is just composed of three parts and it is the minimum parameters to describe the attitude of rigid-body.Suppose σ =[σ1,σ2,σ3]Tto be a Modified Rodrigues parameter21which denotes the reference frameFCrelative toFTand then the attitude matrix is given by

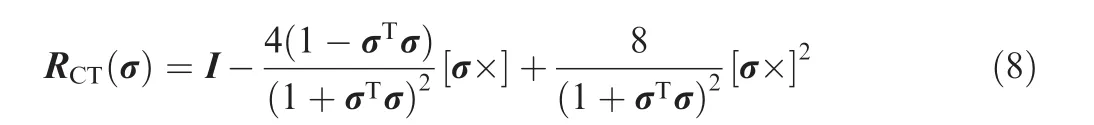
where RCT(σ)is able to transform a vector from frameFTto frameFC.The kinematic equation by the Modified Rodrigues parameters can be shown by

where w expresses the angular velocity of frameFCto frameFT,consequently

where wICand wITare the angular velocities of the chaser and target spacecraft relative to the frameFI,respectively.The first time derivative of Eq.(10)in the frameFIleads to

And according to Coriolis’theorem,it can be directly obtained that

In combination with Eqs.(11)and(12),it easily gets

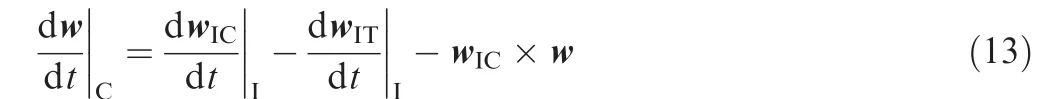
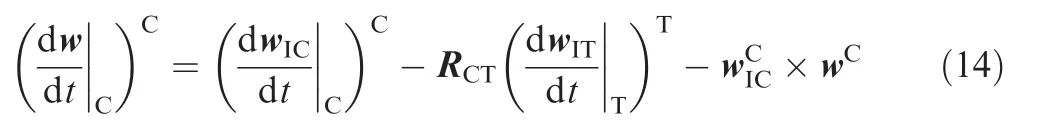
Assume that H and N are the total momentum and external torque of a rigid-body,respectively,then for the chaser spacecraft,

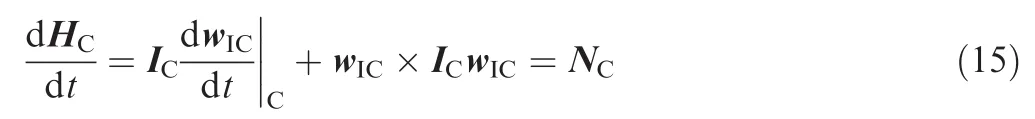
and for the target spacecraft,

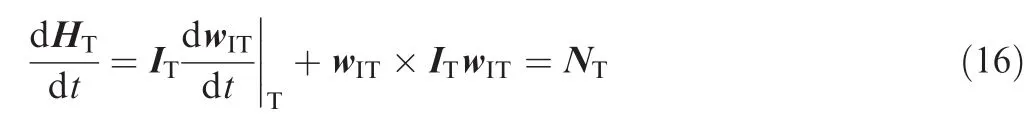
where ICand ITare the inertia tensor of the chaser and target spacecraft,respectively.Notably,since the target is noncooperative,ITis unknown.And this is a major consideration to settle in this paper.Furthermore,it is considered that the target is just disturbed by environmental torque(e.g.,the gravity gradient torque)without control moment.Consequently,NTis able to be considered as a zero-mean white Gaussian process noise with covariance QT.Since H=Iw and combining with Eqs.(14)–(16),the relative rotational dynamic is described by

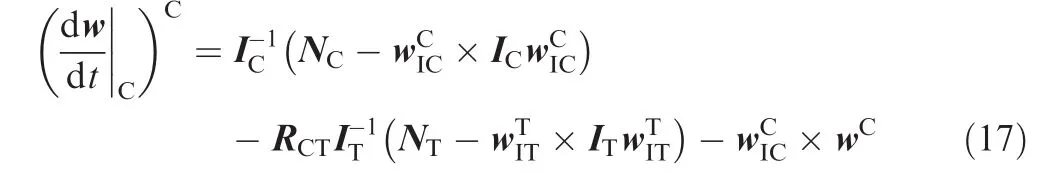
Furthermore,wITis unknown for a non-cooperative target and then Eq.(17)can be written as

3.Rendezvous and docking for non-cooperative target

3.1.Problem statement

In this paper,we aim to estimate the relative states of noncooperative target at the final phase of RVD.A set of points which are acquired by stereo vision are the main external data source,then the state vector x is

where Piis the vector of feature point in Eq.(5)and its corresponding image coordinates are assumed to be processed by speeded-up robust features(SURF)descriptor which is distinctive and robust.22Then,consider a nonlinear continuous-time dynamical system with additive noise described by

where v is zero-mean white Gaussian process noise with covariance Q;f(x)is a nonlinear vector-valued function and its explicit form is referred to Eqs.(1),(6),(7),(9)and(18).Due to the fact that the nonlinear dynamical system is continuous,Eq.(20)is not suitable for computer to calculate its numerical solutions.Fortunately,a method is given by Crassidis to discretize the continuous-time system and a more detail description of the method can be found in Ref.23.

3.2.Observation model

Suppose that a stereo vision system is assembled at the chaser spacecraft(see Fig.2).It consists of a pair of completely parallel cameras with focal lengthf.And the left one which is located at the pointPCis the center of the system,keeping a baseline distanceBaway from the right one.Moreover,it is assumed that the reference of the vision system consists with the body-fixed frame of the chaser spacecraft.Then,an arbitrary feature point Pion the target spacecraft satisfies

where ρi=[ρix,ρiy,ρiz]Tis a vector of line sight between the left camera and the feature point Pi.Project the vector ρionto the image plane and the relationship between R3and R2is described by

wherexiLandyiLconstitute a coordinate of the point Pion image plane of the left camera;xiRandyiRconstitute a coordinate of the point Pion image plane of the right camera.Consequently,the observation model can be written as

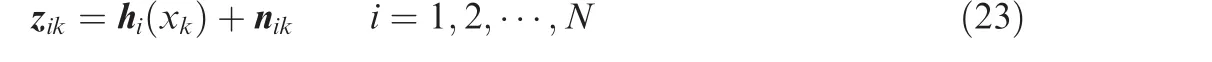
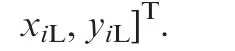
Eqs.(20)and(23)jointly constitute the system model to be processed in this paper.It is notable that the vector of feature point is regarded as a part of the state vector.Accordingly,there is no need to know the precise position of feature point in the reference frameFT.Furthermore,it is not required to capture all the feature points of the target spacecraft.Namely,it means that the proposed algorithm is suitable for the severe conditions of light(e.g.,shadow and occlusion).

Fig.2 Stereo vision system.

4.Estimation methodology

4.1.Dealing with unknown inertia tensor

In this section,the InCKF is introduced to deal with the unknown inertia tensor of target spacecraft.This novel filter we proposed is presented in our previous work24,and here we employ it to estimate the states of relative navigation at the final phase of RVD.Furthermore,algorithm of the InCKF is extended in comparison with Ref.24.The InCKF consists of multiple CKFs and a maximum a posteriori(MAP)calculator.The output of CKFs is taken as the input of MAP calculator to identify which hypothesis about inertia tensor is the best in the present moment.And then,the output of MAP calculator about inertia tensor is treated as a reference input of CKFs.Consequently,the InCKF we proposed is a closed-loop structure.Details of the InCKF are as follows.

The multiple CKFs of the novel approach work concurrently and each is calculated to approximate

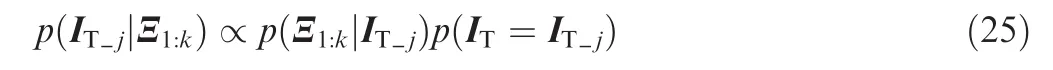
wherep(Ξ1:k|IT_j)is the likelihood of measurements for a period of time conditioned on the inertial tensor IT_j;p(IT=IT_j)is the prior probability about inertial tensor.Recalling multiplication rule,it can be directly obtained that

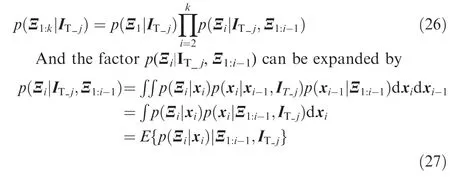
wherep(xi|xi-1,IT_j)is the density function of transition probability and it is evaluated by states Eq.(20).

In Ref.24,we proposed two methods to approximate the likelihood probability which are based on second-order Stirling’s interpolation (SI2)25and unscented transformation(UT)26,respectively.In this section,another method based on spherical-radial rule is proposed to estimate the likelihood probability of inertial tensor.

4.2.Approximation based on third-degree spherical-radial rule

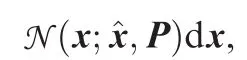
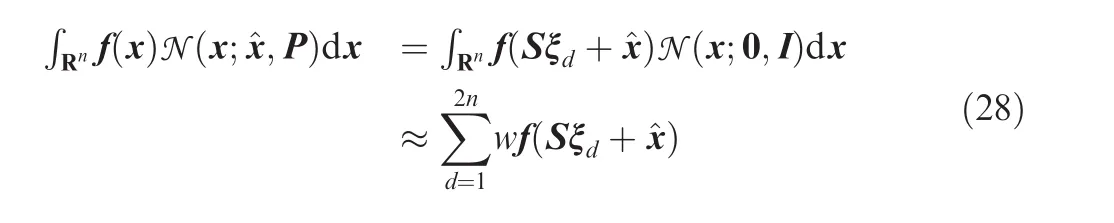
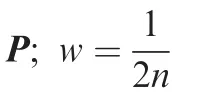
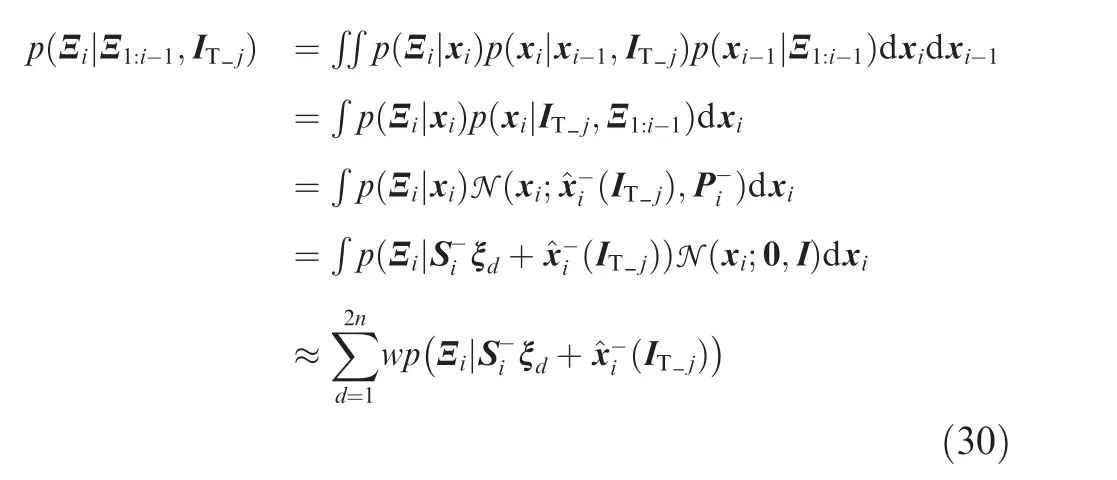
exp(·)is also approximated by the second order Taylor expansion,then

Take logarithm of Eq.(33),which yields

And finally,we take MAP to estimate the most probable inertial tensor

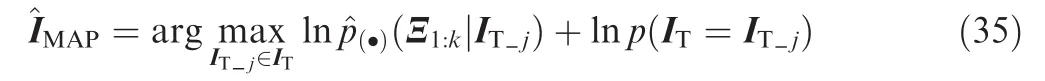
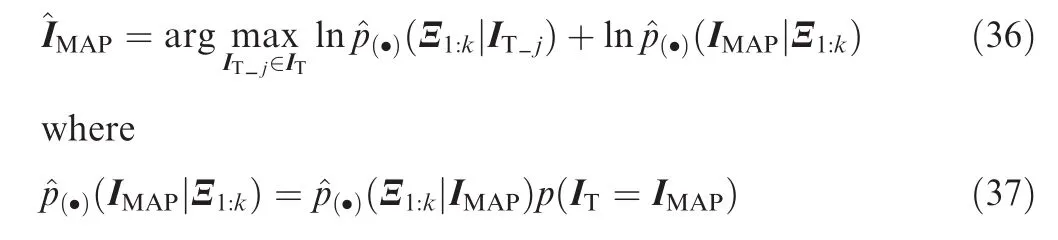
0:=^IMAP;6:for j=0,1,...NIdo 7: Implement CKF using an assumptive inertial tensor IT_jto acquire[^x-k（IT Algorithm 1:Main Framework of InCKF Algorithm 1:Initialization:^x0=0,^IMAP=I,k=0;2:While time k＜finish time do 3: Sample IT_jfrom p(IT),j=1,2,...NI;4: Let ITj）;8: Compute ln^p（Ξ1:k|ITj）and^xk（ITk）using Eq.(34);9:end for 10:Compute the most probable inertial tensor^IMAPusing Eq.(36);11: Set the prior probability p（IT）=^p（·）（IMAP|Ξ1:k）by Eq.(37);12:Set the algorithm’s output as^xk（^IMAP）;13:k=k+1;14:end while

5.Simulation

In this section,two numerical examples are conducted for evaluating the performance of the proposed estimator.Both of the two examples refer to the situation about the final phase of RVD.The first example compares the system model which considers translation-rotation coupling with the uncouple model.In this example,the inertial tensor of target spacecraft is known and the relative states are estimated by CKF.The second example is the major consideration,in which the inertial tensor of target spacecraft is unknown.And the motivation behind this example is to elucidate that the proposed estimator is more robust than EKF to deal with the relative estimation about unknown inertial tensor.The parameters of chaser spacecraft are shown in Table 1.The vision parameters used here are obtained from the Falcon 4M30 camera.

知识服务是出版社转型升级的最终目标。[2]转型升级工程推进以来，共遴选出110家知识服务模式试点单位，包含专业组和综合组，组建了国家知识资源服务中心，有效聚集了专业领域内容资源，夯实了国家知识服务体系建设基础，制定了8项知识服务团体标准，正在研制7项知识服务国家标准。AR知识服务、智能知识服务、大数据知识服务等知识服务的新模式、新业态、新路径正在探索和逐步见效。

In the following examples,we suppose that the locations of the feature points on the target spacecraft are subject to uniform distribution,

5.1.Example I

In the first simulation example,the inertial tensor of target spacecraft is known and its value is the same with that of chaser spacecraft.The initial states are set as follows:

where ρ0(0)is the initial relative position between chaser and target spacecraft,˙ρ0（0）the initial relative velocity,σ(0)the initial relative attitude,w(0)the initial relative angular velocity andn(0)can be obtained from Eq.(3).In addition,the initial states about the feature points in the couple model are given by

And the estimation error eFP of the feature point locations is defined as

The comparisons of states’estimation between couple model and uncouple model are shown in Figs.3–7.Firstly in Figs.3–6,though the state estimation of uncouple model at the initial phase is more fluctuant than that of couple model,their final results are close.It implies that couple model is able to estimate the relative states with the same accuracy as uncouple model.And it means that CKF can elegantly handle highly nonlinear systems and it is still consistent with respect to a higher dimensional system.Secondly,the biggest advantage of couple model is shown in Fig.7.It is obvious that couple model could reach much more accuracy than uncouple modelabout position of feature points.The result of uncouple model is consistent with its initial error for the reason that its states do not refer to the dynamics of the feature points.And the structure recovery of target spacecraft is affected by the estimation precision of the feature points.From the above analysis,we can see that the couple model is more suitable than uncouple model to estimate relative sates at the final phase of RVD with respect to non-cooperative target.

Table 1 Parameters of chaser spacecraft.

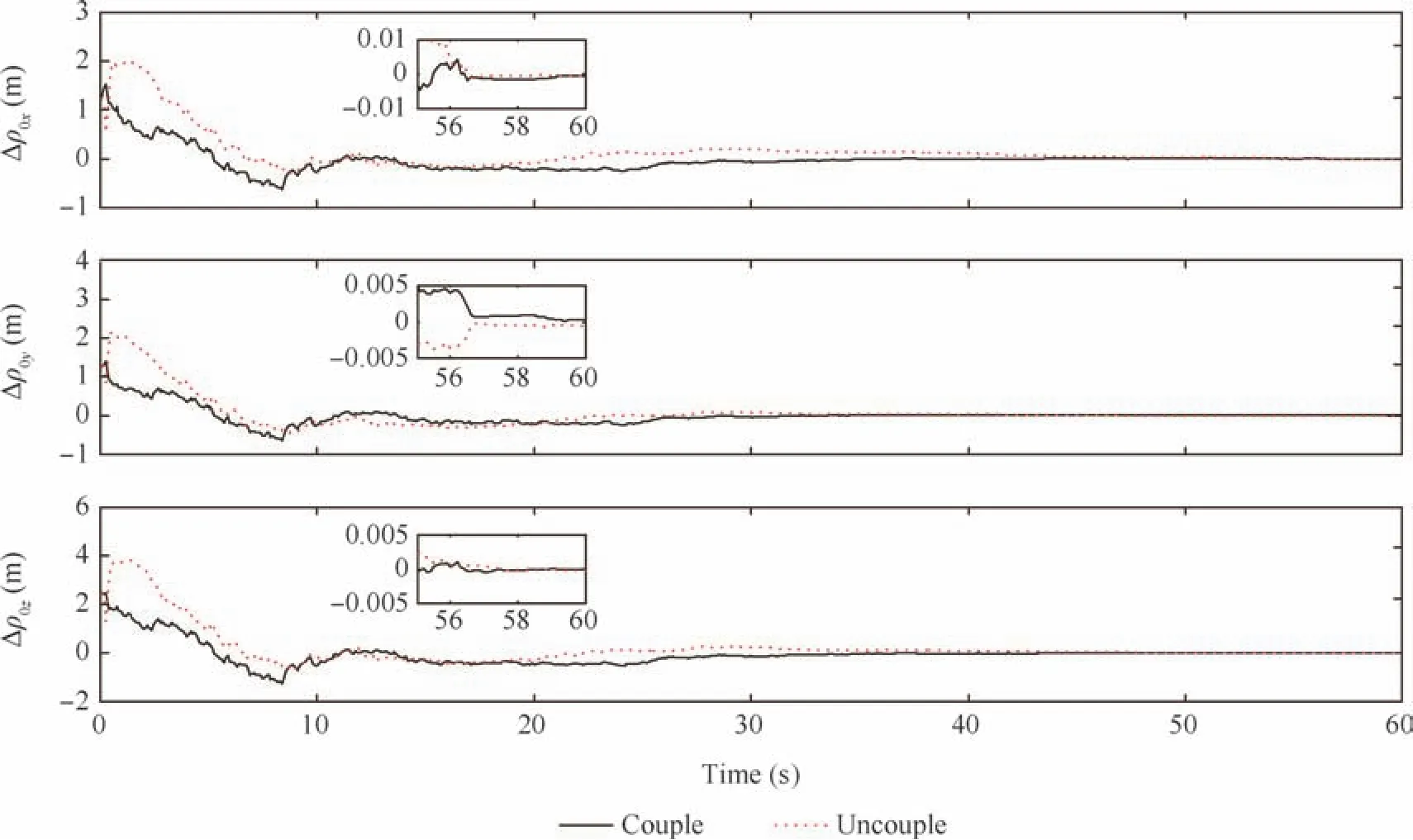
Fig.3 Position estimation errors.

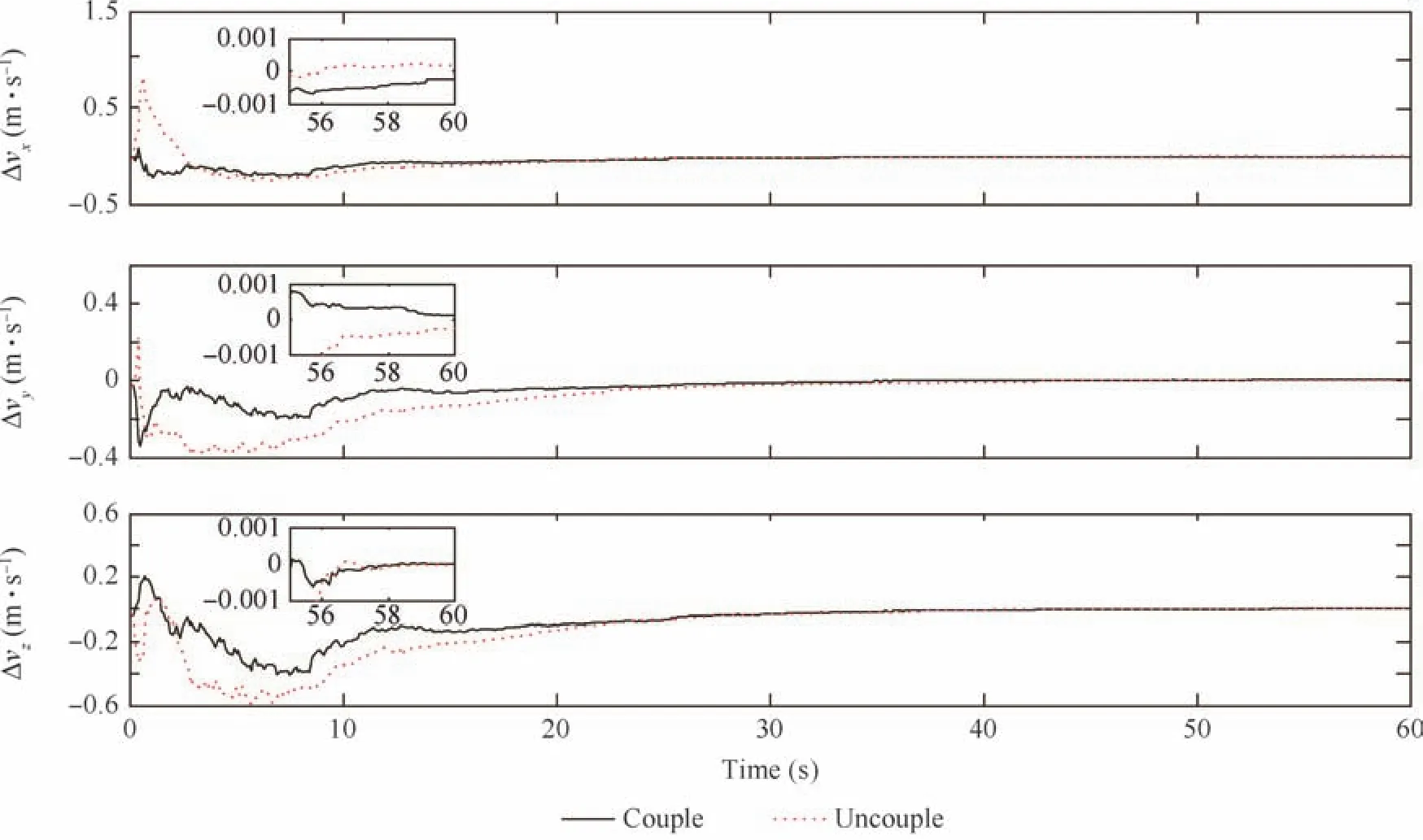
Fig.4 Velocity estimation errors.

5.2.Example II

In this example,InCKF is compared with EKF about relative estimation of unknown inertial tensor.It is supposed that the posteriori probability about inertial tensor of target spacecraft is subject to uniform distribution

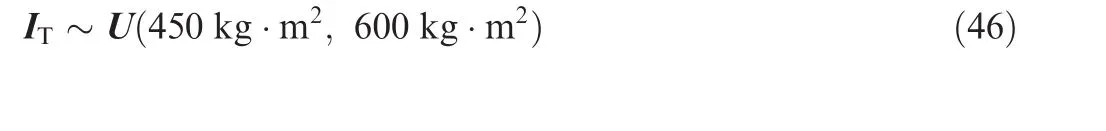
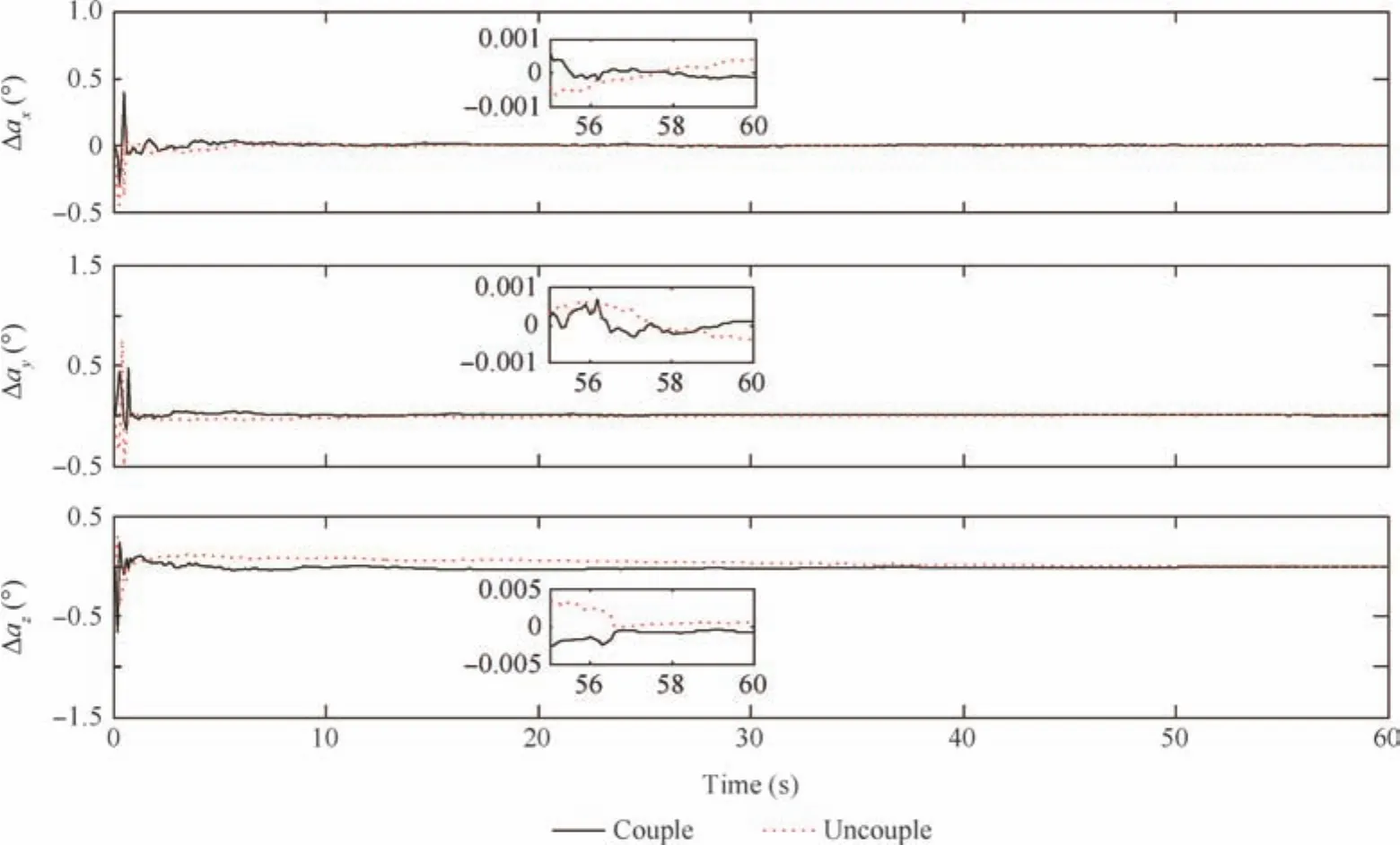
Fig.5 Attitude estimation errors.

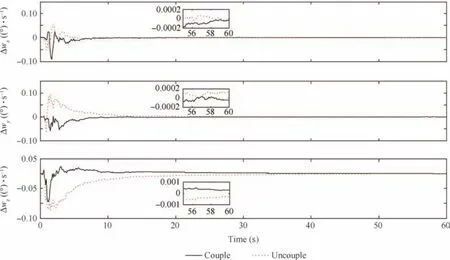
Fig.6 Angular velocity estimation errors.

In each loop of the InCKF,it randomly takes five samples from the uniform distribution as hypotheses inertial tensor.And EKF randomly takes one sample as the target inertial tensor during the whole estimation process.Initial relative position ρ0(0)is set as

And the true inertial tensor of the target spacecraft and the other parameters is the same as those of example I.

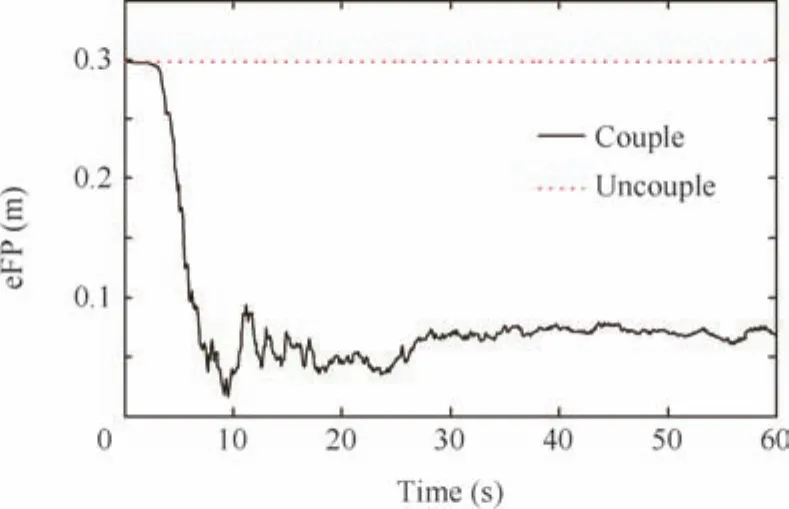
Fig.7 Position of estimation errors of feature points.

Fig.8 Norm value of relative position estimation errors.

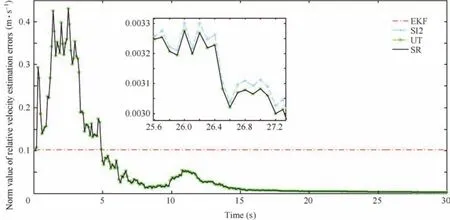
Fig.9 Norm value of relative velocity estimation errors.

Fig.10 Norm value of relative attitude estimation errors.

Figs.8–11 show the norm of relative states estimation errors for this example and Figs.12–15 show the estimation errors.In addition,the norm of inertial tensor estimation errors is shown in Fig.16.In Figs.9–11,the numerical stability of EKF with a random sampling is better than that of InCKF.However its estimation accuracy is worse than that of InCKF in Figs.13 and 14.The difference between consecutive estimation results of EKF is small in Figs.13 and 15,hence its corresponding norm values seem to be constant as compared with that of the InCKF.This is because that the EKF selects random sampling only once for the unknown inertial tensor in the whole estimation process,not like the multiple sampling in the InCKF,whose fluctuation of estimation results about relative velocity and relative angular velocity is small.It is implied that the uncertainty of inertial tensor effects on the estimation results is small in the case of a suitable sampling error.However,in Figs.8,10,12 and 14,there is some saltation at the end of the estimation process.Especially,the results of EKF are jumped in Figs.8 and 10 which could climb up to 0.48 m and 0.35°in a flash,respectively.And it has the trend of divergence.This is extremely dangerous for the RVD missions and it even could result in spacecraft collision.The reason for stability decline is the increase of system dimension.It cannot yield stabilized estimation for all states in the case of high-dimension system.Besides,the nonlinearity at that time is also the reason for this issue.And it implies that the original EKF without any improvement cannot manage the problem of estimation about unknown inertial tensor.Its robustness is worse than that of the InCKF.

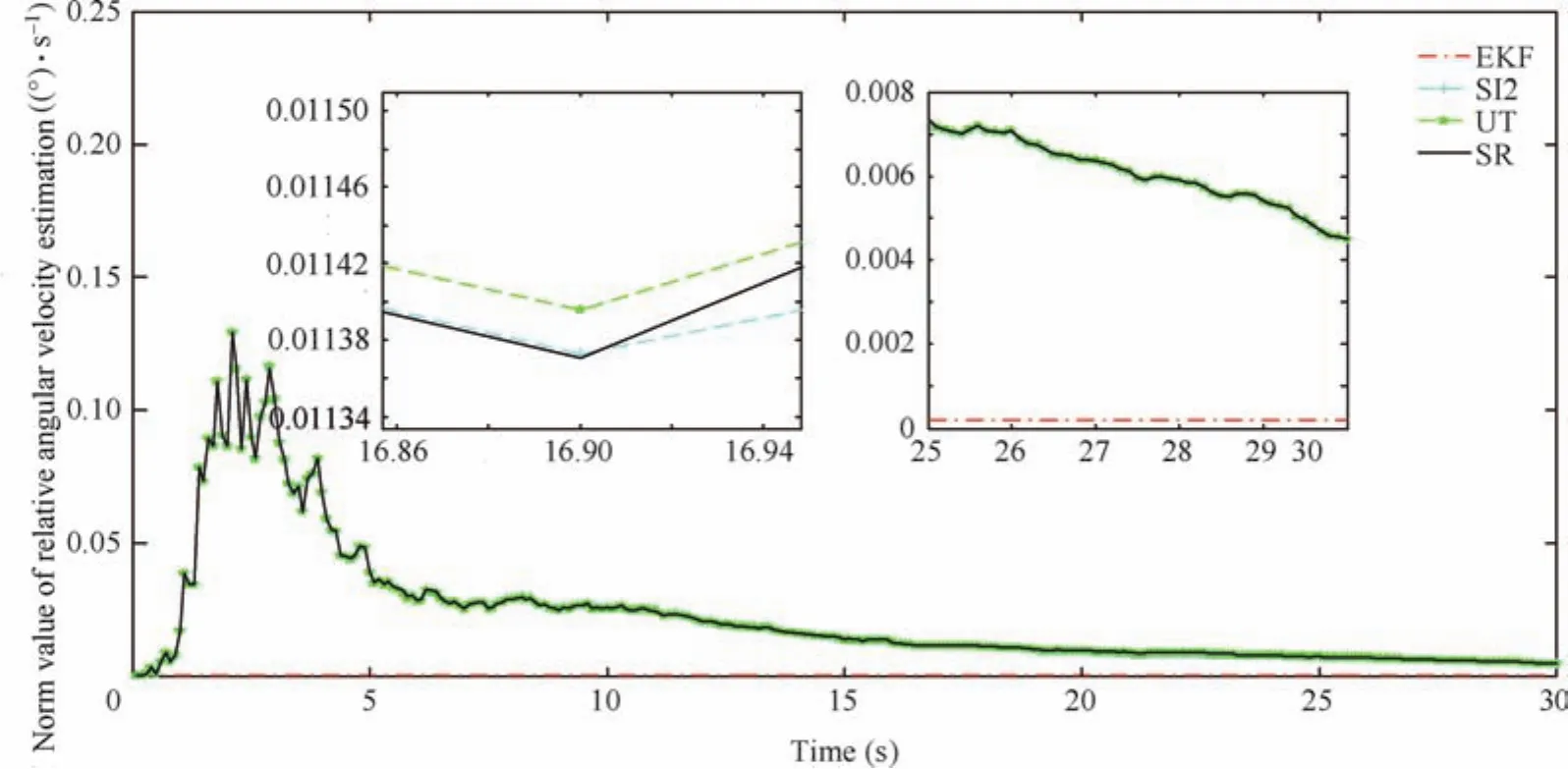
Fig.11 Norm value of relative angular velocity estimation errors.

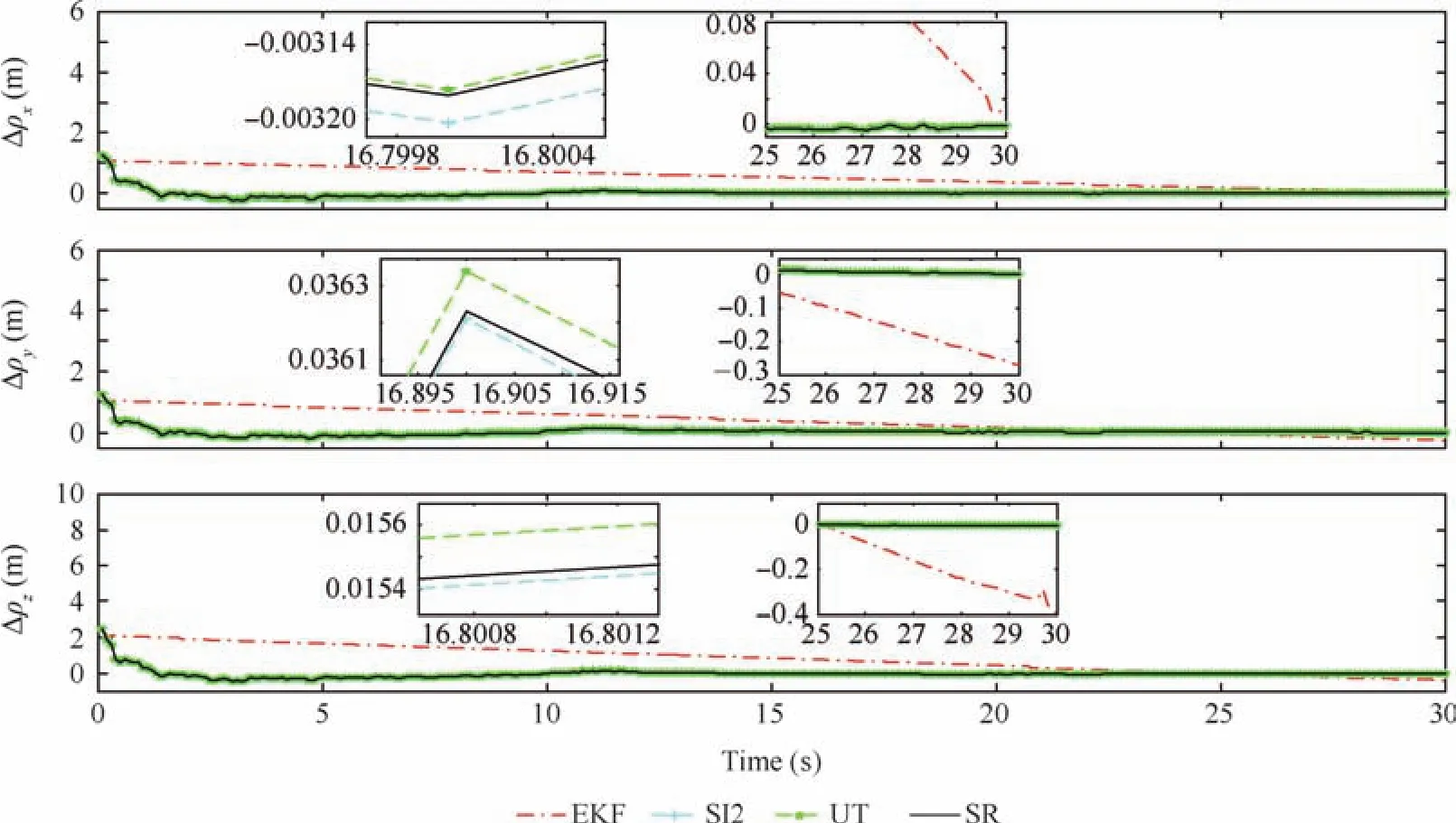
Fig.12 Relative position estimation errors.

Furthermore,it is found that the three kinds of algorithms about InCKF have the same trend and similar accuracy.In Figs.8–15,the accuracies of the InCKF based on Stirling’s interpolation and spherical-radial are a little better than those of the InCKF based on unscented transformation,and their errors are extremely small which are limited within the level of 10-3in Figs.13 and 15.This is because that the main body of InCKF algorithm is still the CKF and the states about relative position,relative velocity,relative attitude and relative angular velocity are estimated by the CKF.Their accuracy is very close and the slight difference is caused by the estimation results about inertial tensor.In Fig.16,the inertial tensor errors of EKF are constant for it randomly samples only once.Although the inertial tensor estimation of InCKF based on Stirling’s interpolation is far better than that of the InCKF based on spherical-radial and unscented transformation,the estimation results with respect to system states are similar.It is implied that the errors of inertial tensor within limits have little effect on the estimation about relative position,relative velocity,relative attitude and relative angular velocity.And the results depend largely on the nonlinear filter.In conclusion,the proposed InCKF can deal with the problems of estimation about unknown inertial tensor effectively and achieve fairly high precision.

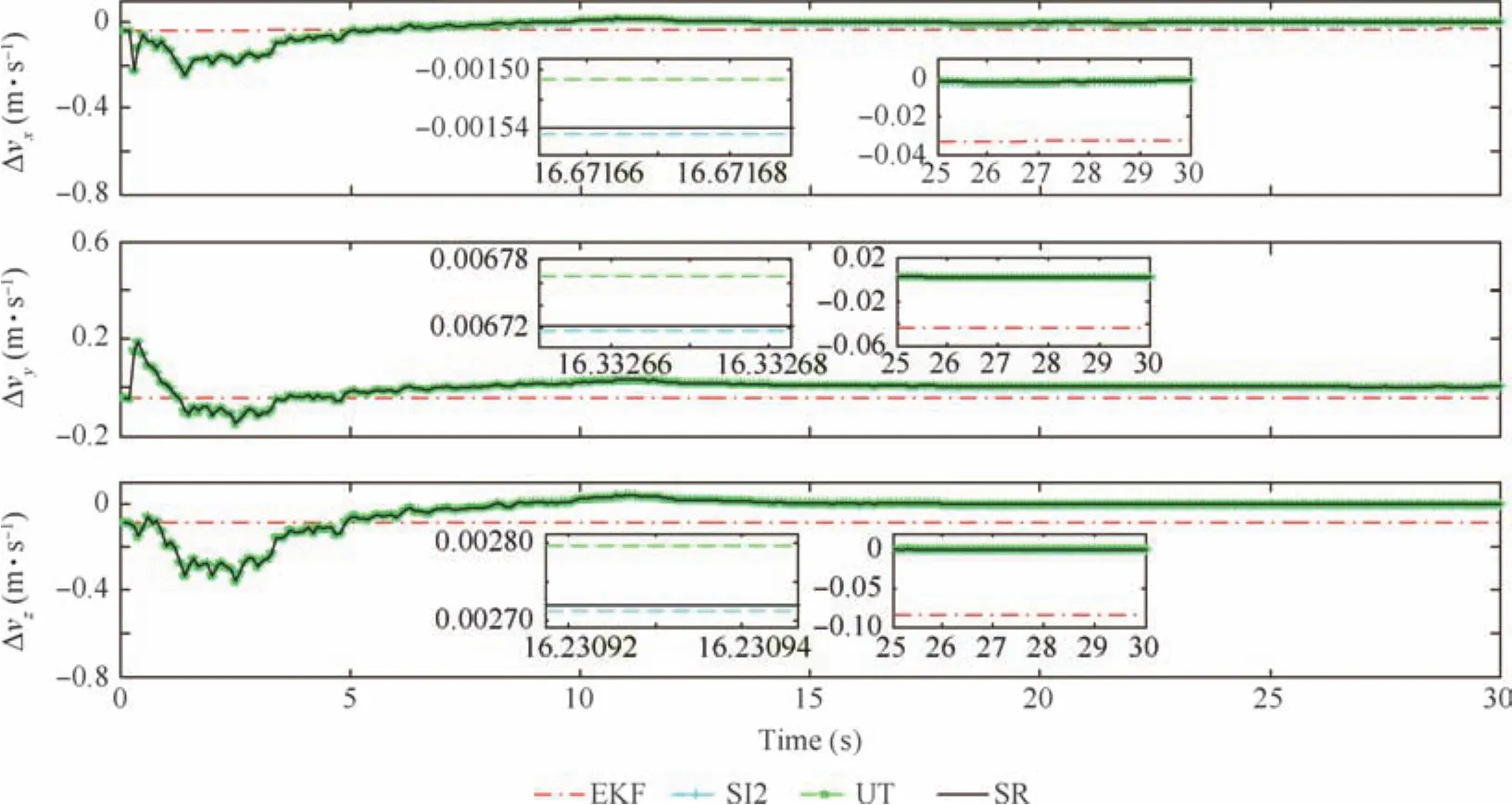
Fig.13 Relative velocity estimation errors.

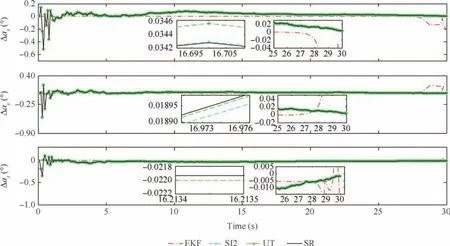
Fig.14 Relative attitude estimation errors.

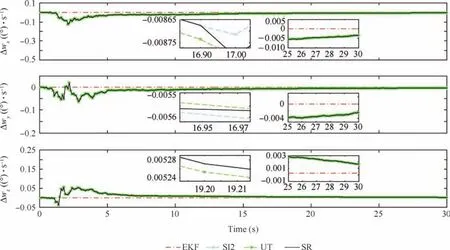
Fig.15 Relative angular velocity estimation errors.

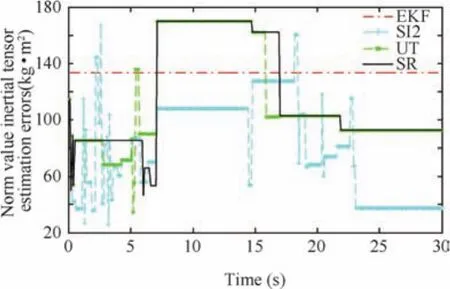
Fig.16 Norm value of inertial tensor estimation errors.

6.Conclusions

(1)A new filter is utilized for estimating the relative states about non-cooperative spacecraft of unknown orbit elements and inertial tensor.This filter integrates a MAP estimator into multiple CKFs to identify the inertial tensor of target spacecraft.And it presents three different methods to approximate the likelihood probability with respect to the inertial tensor.Numerical simulations demonstrate that this filter is much more robust than EKF to unknown inertial tensor.In particular,the accuracy of the filter based on Stirling’s interpolation and spherical-radial rule is extremely high.

(2)Furthermore,this paper presents a coupled model which incorporates kinematic couple between rotational and translational dynamics.And dynamics of the feature points is considered in this couple.Numerical simulations show that the accuracy of the couple model is much better than that of the uncouple model about estimating the position of the feature points.

(3)Different from the traditional dynamics equations which need the orbit elements of the target spacecraft,the relative dynamics in this paper is projected onto the orbital plane of the chaser spacecraft.In the case that there is not any information about the target spacecraft,it is able to satisfy the demand in RVD missions with respect to non-cooperative target well.

Acknowledgements

The authors would like to acknowledge the financial support provided by the National Natural Science Foundation of China (Nos.61174037,61573115),theNationalBasic Research Program of China(No.2012CB821205).

1.Kim SG,Crassidis JL,Cheng Y,Fosbury AM,Junkins JL.Kalman filtering for relative spacecraft attitude and position estimation.J Guid Control Dynam2007;30(1):133–43.

2.Woffinden DC,Geller DK.Navigating the road to autonomous orbital rendezvous.J Spacecraft Rockets2007;44(4):898–909.

3.Wigbert F.Automated rendezvous and docking of spacecraft.New York:Cambridage University Press;2003.p.1–6.

4.Heaton AF,Howard RT,Pinson RM.Orbital Express AVGS validation and calibration for automated rendezvous.Proceeding of AIAA/AAS astrodynamics specialist conference and exhibit;2008 Aug 18–21;Honolulu,Hawaii.Reston:AIAA.2008.p.1–18.

5.Kawano I,Mokuno M,Kasai T,Suzuki T.Result of autonomous rendezvous docking experiment of engineering test satellite-VII.J Spacecraft Rockets2001;38(1):105–11.

6.Pinard D,Reynaud S,Delpy P,Strandmoe SE.Accurate and autonomous navigation for the ATV.Aerosp Sci Technol2007;11(6):490–8.

7.Howard RT,Bryan TC.DART AVGS flight results.Proceeding of sensors and systems for space applications;2007 Apr 9;Orlando,Florida,USA.Washing D.C.:SPIE;2007.p.1–10.

8.Zhang L,Yang H,Zhang S,Hong C,Shan Q.Kalman filtering for relative spacecraft attitude and position estimation:a revisit.J Guid Control Dynam2014;37(5):1706–11.

9.Ambrose R,Wilcox B,Reed B,Matthies L,Lavery D,Korsmeyer D.Robotics,tele-robotics and autonomous systems roadmap technology area 04.Washington DC:National Aeronautics and Space Administration;2010,Draft report.

10.Lanzerotti LJ.Assessment of options for extending the life of the hubble space telescope.Washington D.C.:National Academies Press;2005,Final report.

11.Fasano G,Grassi M,Accardo D.A stereo-vision based system for autonomous navigation of an in-orbit servicing platform.Proceeding of AIAA infotech at aerospace conference;2009 Apr 6–9;Seattle,Washington D.C.,USA.Reston:AIAA;2009.p.1–10.

12.Xu W,Liang B,Li C,Xu Y.Autonomous rendezvous and robotic capturing of non-cooperative target in space.Robotica2010;28(5):705–18.

13.Liu H,Wang Z,Wang B,Li Z.Pose determination of noncooperative spacecraft based on multi-feature information fusion.Proceeding of IEEE International Conference on Robotics and Biomimetics;2013 Dec 12–14;Shenzhen,China.Piscataway,NJ:IEEE Press;2013.p.1538–43.

14.Kelsey JM,Byrne J,Cosgrove M,Seereeram S,Mehra RK.Vision-based relative pose estimation for autonomous rendezvous and docking.Proceeding of IEEE Aerospace Conference;Big Sky,MT.Piscataway,NJ:IEEE Prsss;2006.p.1–20.

15.Zhou J,Bai B,Yu X.A new method of relative position and attitude determination for non-cooperative target.J Astronaut2011;32(3):516–21 Chinese.

16.Segal S,Gurfil P.Effect of kinematic rotation-translation coupling on relative spacecraft translational dynamics.J Guid Control Dynam2009;32(3):1045–50.

17.Aghili F,Parsa K.Motion and parameter estimation of space objects using laser-vision data.J Guid Control Dynam2009;32(2):537–49.

18.Zhang L,Zhang S,Yang H,Hong C,Shan Q.Relative attitude and position estimation for a tumbling spacecraft.Aerosp Sci Technol2015;42:97–105.

19.Segal S,Carmi A,Gurfil P.Stereovision-based estimation of relative dynamics between noncooperative satellites:theory and experiments.IEEE Trans Control Syst Technol2014;22(2):568–84.

20.Arasaratnam I,Haykin S.Cubature Kalman filters.IEEE Trans Autom Control2009;54(6):1254–69.

21.Christopher DK,Hanspeter S.Nonsingular attitude filtering using modifiedRodriguesparameters.JAstronautSci2010;57(4):777–91.

22.Bay H,Ess A,Tuytelaars T,van Gool L.Speeded-up robust features(SURF).Comput Vis Image Underst2008;110(3):346–59.

23.Crassidis JL,Junkins JL.Optimal estimation of dynamic systems.Boca Raton:Chapman&Hall/CRC;2004.p.270–82.

24.Yu H,Song S,Wang S.Interaction cubature Kalman filter and its application.Control and Decision 2015;30(9):1660–6(Chinese).

25.Nrgaard M,Poulsen NK,Ravn O.New developments in state estimation for nonlinear systems.Automatica2000;36(11):1627–38.

26.Julier SJ,Uhlmann JK.Unscented filtering and nonlinear estimation.Proc IEEE2004;92(3):401–22.

27 March 2015;revised 31 August 2015;accepted 27 January 2016

Available online 24 February 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 10 68756947.

E-mail address:yuhanihit@163.com(H.Yu).

Peer review under responsibility of Editorial Committee of CJA.

Yu Hanreceived his Ph.D.degree in control science and engineering from Harbin Institute of Technology in 2015.Currently,he is an engineer at Beijing Institute of Astronautical Systems Engineering.His main research interests include vision-aided inertial navigation,nonlinear filter and effectiveness evaluation.

Zhang Xiujiereceived her M.S.degree in intelligence engineering from Chiba University,Chiba,Japan,in 2006.She received the Ph.D.degree in control theory and application from Harbin Institute of Technology,Harbin,China,in 2013.Her current research interests include evolutionary computation,nonlinear filter and their applications.

Liu Lingyureceived his Ph.D.degree in navigation guidance and control from Beihang University in 2012.Currently,he is an engineer at Beijing Institute of Astronautical Systems Engineering.His main research interests include simulation technology and flight simulation.

Wang Shuoreceived his M.S.degree in control science and engineering from Heilongjiang University in 2011.Currently,he is a Ph.D.student at Harbin Institute of Technology.His main research interests include vision navigation,nonlinear filter and data fusion.

Song Shenminreceived his Ph.D.degree in control theory and application from Harbin Institute of Technology in 1996.He carried out postdoctoral research at Tokyo University from 2000 to 2002.He is currently a professor at the School of Astronautics,Harbin Institute of Technology.His main research interests include spacecraft guidance and control,intelligent control,and nonlinear theory and application.