Instability and sensitivity analysis of flows using OpenFOAM®

Liu Qiong,F.Gómez,J.M.Pérez,V.Theofilis

aSchool of Aeronautics,Universidad Politécnica de Madrid,Plaza Cardinal Cisneros 3,Madrid E-28040,SpainbDepartment of Mechanical and Aerospace Engineering,Monash University,Victoria 3800,Australia

Instability and sensitivity analysis of flows using OpenFOAM®

Liu Qionga,*,F.Gómezb,J.M.Péreza,V.Theofilisa

aSchool of Aeronautics,Universidad Politécnica de Madrid,Plaza Cardinal Cisneros 3,Madrid E-28040,SpainbDepartment of Mechanical and Aerospace Engineering,Monash University,Victoria 3800,Australia

Adjoint-based analysis;Computational fluid dynamics;Flow instability;OpenFOAM;Time-stepping method

The present contributions deal with the development and implementation of the direct and adjoint incompressible Navier–Stokes equations in a matrix-free time-stepping context making use of the open-source OpenFOAM®(open source field operation and manipulation)C++toolbox.It is shown that a few minor modifications in the source code can enable these multi-purpose computational fluid dynamics(CFD)solvers to carry out global instability analysis of threedimensional flows of engineering interest,exploiting all additional capabilities of such codes.The strength of this methodology is demonstrated through the analysis of an interesting selection of open and wall-bounded flows.

1.Introduction

The studies of hydrodynamic instabilities arising in many flows of engineering relevance are of great importance in order to understand the transition process from a laminar to a turbulence state.This kind of studies,known as global istability analyses,1,2are performed by employing the direct and adjoint Navier–Stokes equations(NSE)linearized around a base flow,traditionally implying the development of a specific solver for each different flow.In this context,recent advances in CFD software have been provided to the computational fluid dynamics community with a great variety of open-source solvers and tools,such as Stanford University Unstructured(SU2),3Nek5000,4Nektar++5,6or OpenFOAM®(open source field operation and manipulation),7among many alternatives.From an academic point of view,the major advantage of the use of these numerical solvers against the proprietary software,besides license related issues,is the access to the source code and the possibility of customizes it for multiple purposes.In addition,these suits allow the use of multiple pre-and post-processing tools such as parallel processing or mesh creation/manipulation utilities,whose availability a priori can save significant effort and time in obtaining results from numerical simulations.

In parallel to this,most of the advances in global instability analysis of flows have been closely related to the computational resources available.As example,global instability analyses of three-dimensional flows in complex geometries,i.e.,three non-homogeneous spatial directions,also known as TriGlobalproblems1,were not affordable untilveryrecently.8–10Consequently,the contributions of global instability theory to the aerospace field have developed an exponential growth in the past years,as stated by Theofilis.1,11Examples of the breakthroughs are the natural extension of the Orr-Sommerfeld equation12to two-and three-dimensional problems,known as BiGlobal13–15and TriGlobal8–10problems respectively, receptivity theory,16,17transient-growth,18–21direct-adjoint-based flow control22–25or even providing further insight on acoustic phenomena.26,27The goal of this work is to present a methodology for the development of global direct and adjoint stability analysis based on modification of the existing open-source CFD software,able to exploit all their above mentioned advantages of the open-source packages.Note that while previous works have focused on describing how to exploit generic solvers,such as Fosas de Pando et al.28and Alizard et al.,29or specific in-house codes,such as Browne et al.30and Ferrer et al.,31only the work on Peplinski et al.32provides information on how to perform global instability analysis with the open-source code Nek5000.Here,the Open-FOAM®toolbox has been selected for this purpose because its previous success in this field deals with complex threedimensional flows.10,33–36The validation of the method has been carried out with well-known but challenging cases;the global direct and adjoint instability analysis of the flow around a cylinder,the flow over a 2D and 3D open cavity and the flow confined in a cubic lid-driven cavity.

2.Theoretical fundamentals

The motion of a 3-D incompressible viscous flow is described by the following continuity equations and the dimensionless Navier–Stokes equations in Cartesian coordinates:

whereReis the Reynolds number defined as,

withUbeing the reference velocity,Lthe length reference,μ the kinematic viscosity,the velocity vectors u=[u，v，w]expressed in Cartesian coordinates(x,y,z)andpthe modi fied pressure.The mathematical problem is closed with proper boundary conditions for velocity and pressure depending upon the flow subject to study.A linearized problem can be obtaining by decomposing the flow in a steady base flow u(x,y,z)and a three-dimensionalunsteady smallperturbations∈u′（x，y，z，t）with ∈≪ 1.The linearized Navier–Stokes equations are obtained by retaining theO（∈）terms

Eq.(5)can be written in a compact form as

where the operator A is the Jacobian matrix of the right hand side of the Navier–Stokes equations.According to the TriGlobal ansatz1,solutions of Eq.(6)are sought as eigenmodes

where λ= λr+iλi,λiwith representing the frequency,λrthe amplification/damping rate of the sought perturbation and c.c.the complex conjugate.Finally,the combination of the Eq.(7)with Eq.(6)leads to the following eigenvalue problem

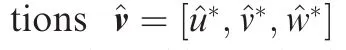
These adjoint equations can be written in a similar fashion to the linearized Navier–Stokes Eqs.(4)and(5)as

Similarly to the direct case,Eq.(11)is rewritten in a compact form,

By perturbing the direct eigenvalue problem Eq.(8)it is obtained that

and using the adjoint relation(9)leads to a relation between the change induced in the eigenvalue δλ by the modification of the Jacobian-matrix,

If a spatial localized perturbation as δA=δ（x-x0，y-y0，z-z0）is introduced in the above equation,it is possible to define a function that localizes the spatial positions where the λ eigenvalue is most sensible to perturbations of the Jacobian-matrix through small changes in the base flow,enabling the possibility of suppressing instability onsets by small modifications in the base flow,as done experimentally by Strykowski and Sreenivasan,37which leads to

The derivation of the adjoint operator can be found in multiple classical textbooks,e.g.Golub and van Loan38or Morse and Feshback,39where the most critical step is deriving proper boundary conditions for the treatment of the bilinear concomitant.In what follows,the derivation is omitted for simplicity and the adjoint equations will be presented with correct boundary conditions that satisfy a zero bilinear concomitant.Further details about the construction of the adjoint operator,the corresponding boundary conditions and their use to determine the structural sensitivity of the eigenmodes can be found in the works of Hill,22Giannetti and Luchini.25The next section will be focused on the required modifications to OpenFOAM®for the extraction of the direct and adjoint eigenmodes in a time-stepping matrix-free context,as performed by Tuckerman and Barkley40and Barkley et al.18

3.Numerical method

3.1.Direct and adjoint linearized Navier–Stokes equations

The development of the direct and adjoint linearized Navier–Stokes equations by modifying the incompressible transient solver of the open-source CFD software OpenFOAM®,named icoFoam is shown next.This solver,based on a classical finite volume formulation41and a pressure-implicit with splitting of operators(PISO)41–43algorithm,has demonstrated a highquality performance in the recent literature.10,33–35This algorithm and its modifications to create solvers for the linearized and adjoint Navier–Stokes equation,named dirIcoFoam and adjIcoFoam respectively,are explained here in detail.The key idea of the PISO algorithm is that for small time steps the pressure–velocity coupling is much stronger than the non-linear convective coupling,therefore it is possible to split the solution into a set of corrections where the pressure is decoupled from the velocity,since the velocity in the momentum equation dose not need to be updated for each pressure correction.Although this procedure is not formally necessary to solve the LNSE,since these equations are linear,the PISO method of solution can be applied in order to treat in an explicit manner the convective term in which the volume flux contribution of the perturbation velocity needs to be evaluated,as it is detailed next.

A similar notation to Jasak43will be employed in what follows.As an example in streamwise direction,the semidiscretization of the convective term of the Navier–Stokes using finite volumes in a polyhedron is written as

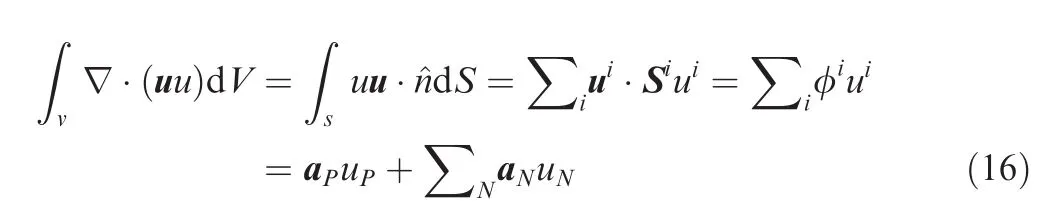
where the velocity is evaluated on the facesiof the polyhedronP,Siis the normal vector to faceiwhich norm equal to the face area,φiis flux on facei,aPand aNare the function of u,and subscriptNrepresents the neighbors polyhedron toP.Finally,the flux φiis obtained by interpolation of the node values adjacent to each surface.Taking this formulation into account,the momentum equation of the Navier–Stokes Eq.(2)can be equivalently defined and initialized as

aPcontains the discretization matrix operator of the implicit term while H（u）represents the explicit terms of the velocity.The first two terms of the above equations are represented in Line 1 of Listing 1 in OpenFOAM®notation,where fvm is the namespace,which is defined as the implicit version of the operators(ddt,div or laplacian).A momentum predictor is then obtained using the momentum equation and the pressure from a previous step,which in OpenFOAM®notation is written in Line 3 of Listing 1.

Recalling Eq.(17),the explicit terms can be written as

This term is represented in Lines 5 and 6 in Listing 1,where the functions UEqn.A()and UEqn.H()extract the implicit and explicit terms from Eq.(17).The momentum equation is then written as

where the left hand side term is divergence-free and the continuity equation can be applied to obtaining the laplacian equation:

in which the left hand side can be treated explicitly.Next the velocity flux φ is updated with the new velocity,which permits the obtention of the new pressure field,as seen in Lines 8 and 9 in Listing 1.

Finally the divergence-free velocity u is corrected with the correct pressure gradient with Eq.(17)and the last step of the PISO algorithm consists of advancing the time-step.Non-orthogonality effects,boundary conditions corrections and details about the discretization have been omitted for simplicity.This PISO algorithm is summarized in Algorithm 1(see the Appendix A).This algorithm can be easily modified in order to solve the direct and adjoint linearized Navier–Stokes equations.It is trivial to observe from Eqs.(5)and(10)that the main difference with the full Navier–Stokes equations are the additional advection terms and the different signs in case of the adjoint equations.Since the terms related with the base flow are constant,and the predictor fluxes of the perturbation are constructed with the perturbation velocity from previous step,the additional advection term of direct and adjoint equations can be formed in a explicit manner,thus the equations to be solved are equivalent to the non-linear case.In other words,the base flow advection term can be treated as a source term.Therefore,dirIcoFoam and adjIcoFoam solvers for Eqs.(5)and(11)can be constructed by modifying the matrix UEqn with adding the new advection term.The source code of dirIcoFoam is represented in Listing 2,where U refers now to the perturbation,UB is the base flow and fvc is the namespace,which are,defined the explicit version of the operator(div).

Similarly,the adjoint equation solver dirIcoFoam is represented in Listing 3,where V refers to the adjoint perturbation.Note that special treatment of the temporal scheme is required forthebackwardstemporalintegration oftheadjoint equations.

Listing 1.Projection step

Listing 2.Correction step in dirIcoFoam

Listing 3.Correction step in adjIcoFoam

3.2.Global instability analysis

Two different methods are presented for the new solvers dirI-coFoam and adjIcoFoam,as shown in Algorithm 2 and Algorithm 3(see the Appendix A).Algorithm 2 shows the power iteration method.In the steady flow,the leading eigenmode preserves its initial magnitude and the others eigenmodes are damped while the temporal integration,frequency λiand damping/growth rate λrof the leading eigenmode can be extracted using the time history date.This is achieved by fitting time history date of any flow variable to prescribed oscillatory exponential solution Eq.(7)via a standard least-square approximation.Once damping/growth ratio is obtained,the residual algorithm developed by Theofilis44is used to determine the real^urand imaginary part^uiof the spatial eigenmode^u.This consists of writing solution Eq.(7)at two different timest1andt2with two unknown parameters^urand^ui

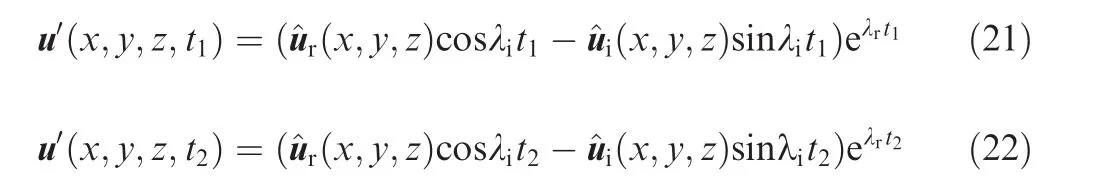
leading to a easily solvable linear system.Since this method is solely based on power iterations,the present algorithm can only provide the structural sensitivity of the leading eigenvalue of the flow,which is the responsible for the onset on the instability.In addition,this method is equivalent to the temporal integration,so it converges as ～ e|λ1-λ2|τ,thus this algorithm is very effective when a gap between first and second eigenvalue is expected in the spectrum.In addition,because of this,the computational resources employed in terms of CPU time in the analysis can be significantly smaller to those required in the obtaining of the steady base flow using a transient method.Algorithm 3 shows the implementation of this methodology employing the solvers dirIcoFoma and adjIcoFoam.Alternatively,Krylov-subspace projection methods,such as those described in Tuckerman and Barkley40and Barkley et al.,18are straightforward to implement with the dirIcoFoam and adjIcoFoam solvers.Particularly,this is the preferred method in case the obtaining of a larger subset of the spectrum is required.

4.Results

4.1.Sensitivity of flow past a circular cylinder

The well-known example of the cylinder wake flow has served as validation of the present methodology.A similar mesh to the one employed in the work of Gómez et al.45has been used for the generation of a base flow atRe=40.The boundary conditions for the direct instability analysis are derived straight forward from the linearization of the boundary conditions used for the base flow.The derivation of the adjoint boundary conditions is not trivial,and the reader can refer to the works of Barkley et al.18or Giannetti and Luchini.25The details of the boundary conditions used in the direct and adjoint instability analysis are summarized in Table 1.We employ Dirichlet for velocity and Neumann for pressure at inlet and cylinder surface,while both Dirichlet and Neumann are employed at the outlet.Although this outflow boundary condition is not formally correct,it can beimposed in the computational domain,which is large enough for the adjoint mode to be vanished at the far-field,as indicated by Barkley et al.18Fig.1 shows the structural sensitivity of the first instability of the cylinder flow δλ（x，y）atRe=40 corresponding to an eigenvalue λ1=-0.03+i0.126 in excellent agreement with the results from Refs.25,46It can be seen that the structural sensitivity function is confined inside the computational domain,proving that the employed domain is large enough for the present calculations.Moreover,this figure is in perfect agreement with those available in the literature25and indicates the instability mechanism is located in two lobes placed symmetrically inside the separation bubble.

Table 1 Summary of boundary conditions used in direct and adjoint cases.

Fig.1 Contour plot of structural sensitivity of the first instability of cylinder flow δλ（x，y）at Re=40.

4.2.Flow over a 2-D open cavity

Open cavity flow,as an interesting topic in the fluid mechanism,has been researched more than half a century.Here we focus on the recovery of the shear layer instability which is well known in the 2-D open cavity case and has been described in detail by Rossiter.47The cavity configuration and flow conditions are controlled by the ratio of the cavity length to depthL/D,the Reynolds number depends on the cavity depthRe=UL/v,the ratio of the cavity length to the initial boundary layer momentum thickness at the leading edge of the cavity isL/θ and δ*is the boundary layer displacement thicknsess.Note that the Reynolds number based on the displacement thicknessReδ*almost remain constant for the two different studied cases atRe=1400 andRe=1900,as shown in Table 2.

Table 2 Parameters of 2D open cavity with aspect ratio L/D=2.

Table 3 Grid convergence based on velocity u for the 2D open cavity at Re=1400 using three meshes.

The Richardson48extrapolation generalized by Roache49is employed for the mesh refinement study,as previously employed by Sanmiguel-Rojas et al.33A grid convergence index(GCI)is defined as

The inflow,wall and outflow boundary conditions for the direct and adjoint instability analysis are the same as the preceding cylinder case.Table 1 shows these boundary conditions.

Fig.2 shows the time evolution of the residual of kinetic energyE(t)from the direct numerical simulation(DNS)of the 2D open cavity flow atRe=1400.The constant of slope corresponds to the damping rate of the least stable stationary mode λ =0.0179,where ΔE=E（t）-E0,E0is the convergence value of kinetic energy.This value is in good agreement with the spectrum obtained by de Vicente et al.50

Fig.2 Mesh and time evolution of kinetic energy residual of 2D open cavity at Re=1400 by DNS.

Table 4 Eigenvalues of the least stable mode get by residual algorithm for2D open cavityflow atRe=1400and Re=1900 with DNS(icoFoam),direct instability analysis(dirIcoFoam) and adjoint linear instability analysis(adjIcoFoam).

The recovered eigenvalues calculated by three different solvers can be seen in Table 4.Figs.3 and 4 show the corresponding eigenfunctions of these least stable eigenvalues.AtRe=1400,we can see in Fig.3 that the flow structure associated with the stable steady eigenvalue is confined inside of the cavity,indicating that the shear layer effect does not dominate the flow features atRe=1400.In agreement with this,Brés and Colonius51pointed out that at the subcritical conditionRe=1500 the shear layer mode damps fast and the oscillation frequency can only be measured at early times,which proves that this stationary mode is dominant at those values of Reynolds number.Fig.5(a)shows thatthe structural sensitivity of this stable mode is con fined inside the cavity.As the Reynolds number increases to a supercritical value ofRe=1900,the dominant 2-D global mode of the open cavity flow is no longer related to the cavity and it is dominated by the shear layer effects,as seen in Fig.4.Correspondingly,the structural sensitivity of the eigenvalue now lies on the shear layer over the cavity,as shown in Fig.5(b).

4.3.Flow over a 3-D open cavity

Fig.3 Real part of direct eigenmode^u.^v and real part of adjoint eigenmode^u*,^v*of open cavity at Re=1400.

Fig.4 Real part of direct eigenmode^u,^v and real part of adjoint eigenmode^u*,^v*of open cavity at Re=1900.

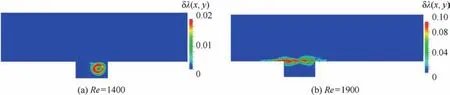
Fig.5 Sensitivity function δλ（x，y）of two-dimensional open cavity.

The structural sensitivity of the flow over a three-dimensional cavity is studied here.The instability analysis of this flow has been and is still the subject of several studies,specially focusing on the self-sustained oscillation of the shear layer,52–54known as shear layer mode or Rossiter mode.48However,different from the two-dimensional case,this configuration also presents a three-dimensional instability.Brés and Colonius51seem to be the first to point out the three-dimensional instability of the open cavity,which arises from a centrifugal instability mechanism associated with the main recirculate vortex in the rear of cavity.In addition,de Vicente et al.50investigate the early stage of the three-dimensional flow associated with centrifugal effects around the recirculation vortex inside the cavity,and the result shows that the shear layer effects are not dominant in the nonlinear saturated state.

Like in the previous 2-D case,the instability of the flow over the open cavity with an homogeneous spanwise spatial direction is investigated with the three-dimensional linearized and adjoint linearized Navier–Stokes equations following the Algorithm 2.In this case,the base flow used in the three-dimensional linear instability analysis relies on the existence of a 2D steady base flow with a Fourier expansion along the spanwise homogeneous direction.All the parameters governing the flow are sketched in Fig.6(a)and stated in Table 5.Notice that in addition to the two-dimensional case parameters,a spanwise extent Λ is introduced as additional parameter.

In agreement with the resolution study in Table 3,mesh M2 is preformed with a spanwise extrusion of uniform 15 cells inzdirection.The inflow,wall and outflow boundary conditions of the direct and adjoint instability analysis are the same as the 2D open cavity case.

As an additional validation,the shear layer spreading rate along the cavity length,defined as δω,54is measured.We find that for the present simulation the spreading rate δω=0.0482 with a thicknessL/θ =51.948 is in agreement with the values presented by Rowley et al.54δω=0.05 with a thicknessL/θ=53.

Fig.6 Open cavity configuration,|^u1|direct eigenmode,|^v1|adjoint eigenmode and sensitivity function δλ（x，y，z）of 3D open cavity at Re=1400.

Table 5 Parameters of 3D open cavity with aspect ratio L/D=2.

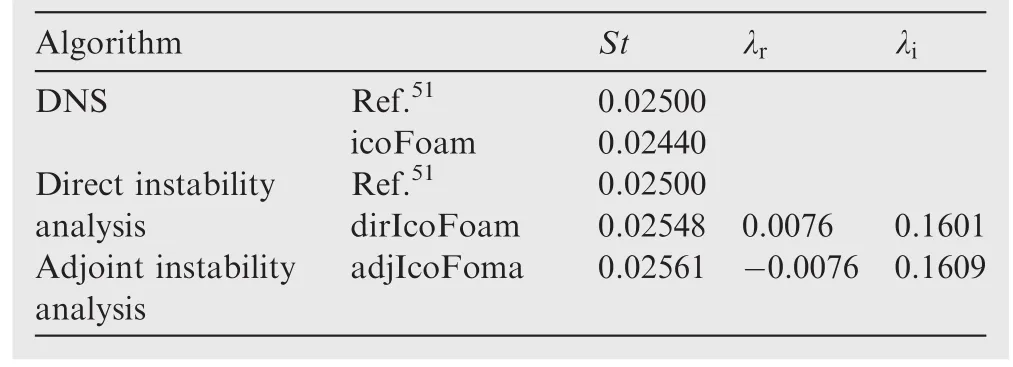
Table 6 Comparison of leading mode of 3D instability results from the open cavity by residual algorithm.

Table 6 shows the 3D instability results,indicating that growth/damping rate λr,frequency λiand Strouhal numberSt= λiD/2πUare in good agreement with previous work from Brés and Colonius.51Fig.6(b)shows the modulus of the velocity|^u1|of the first instability mode atRe=1400,which corresponds to an unstable configuration because of the positive growth rate.Translucent and solid isosurfaces represent a normalized value of 0.2 and 0.5 respectively.The direct mode rotates around the primary vortex inside the cavity,thus it is originated by a 3D centrifugal instability mechanisms,as observed by Brés and Colonius.51Fig.6(c)indicates that adjoint mode|^v1|is also confined in the cavity.As a consequence,the structural sensitivity of this eigenvalue must be located in the cavity as well.It is worthwhile to note that the adjoint mode near the upstream lip is not negligible.The spatial distribution of the product between the direct mode and the adjoint mode δλ（x，y，z）is displayed in Fig.6(d).This result indicates that the ‘‘wavemaker”region(e.g.Giannetti et al.25)of this flow is located inside cavity.

Fig.7 Direct and adjoint spectra,|^u1|direct eigenmode,|^v1|adjoint eigenmode and δλ（x，y，z）of cubic lid-driven cavity at Re=1000.

4.4.Flow inside a cubic lid-driven cavity

Thedirect-adjointinstabilityanalysishasalsobeenappliedtothe wall-bounded 3D lid-driven cavity flow,which corresponds to a TriGlobalproblem,asafinalexampleofthecapabilityofthepresentmethodologies.Note thatthisTriGlobal problem isthe only one relatively well-known and reference spectra can be found in the recent literature.10,25,55,56A steady base flow atRe=1000 has been obtained by means of the long-time integration of the transient solver icoFoam using an identical mesh as in the work ofGómezetal.10atthesamevalueofReynoldsnumber.Dirichlet and Neumann boundary conditions are imposed for the adjoint velocity and adjoint pressure respectively in all boundaries.

Fig.7(a)shows the obtained direct and adjoint spectra using the Algorithm 3,which are in excellent agreement with previous analysis10,56,GLM and GGT refer to results by Giannetti et al.56and Góme et al.10respectively using a 643 resolution.Concerning computational costs of the analysis,the linearized solvers inherit concurrent execution capabilities from the transient solver icoFoam,thus the computational expenses are similar to the ones showed in Gómez et al.10Fig.7(b)and(c)show the normalized spatial distribution of the velocity field modulus of direct and adjoint leading eigenfunction respectively,corresponding to λ1=-0.1292 ± i0.319,translucent and solid isosurfaces represent a normalized value of 0.3 and 0.7 respectively,lid moves in positivex-direction.

The spatial distribution of the product between these direct and adjoint eigenfunctions δλ（x，y，z）is shown in Fig.7(d).The large overlapping of the direct and adjoint eigenfunctions indicates that the Jacobian matrix of this flow presents small nonnormality.This result is consistent with the literature,since this kind of wall-bounded flows does not exhibit large transient growth.57Interestingly,the relevance of the end-wall affects the three-dimensional global mode.Flow control based on this feature could be exploited in a future work.

5.Conclusions

Specific details on the required modification for providing the open-source toolbox OpenFOAM®with global instability and sensitivity analysis tools have been provided.The presented methodology has been successfully validated against a large number of well-known configurations of open and wallbounded flows.As a result,this methodology has proved to be a new effective tool for further research in the global instability field.

Acknowledgement

Support of the Marie Curie Grant PIRSES-GA-2009-247651‘‘FP7-PEOPLE-IRSES:ICOMASEF — Instabilityand Controlof Massively Separated Flows” is gratefully acknowledged.

Appendix A.

Algorithm 1.PISO algorithm

Algorithm 2.Sensitivity analysis with direct and adjoint power iteration

Algorithm 3.Sensitivity analysis following Barkley et al.18 methodology

A2.Ajoint problem:Solve adjoint EVP(12)B1.Initial condition adjoint problem:Set m,∈and v′l B2.Arnoldi iteration:Perform until convergence(l=1,2,...,m)C1.Call adjIcoFoam:v′l ← eAτv′l C2.Gram-Schmidt orthonormalization:(i=1,2,...,l)D1.From Hessenberg matrix h*D2.Orthogonalize v′l+1=eA*τv′l- ∑ji=1h*ilv′i il=v′TieA*τv′l D3.Normalize h*l+1，l=||v′l+1||,v′l+1=l+1 h*l+1，l v′B3.QR:Perform eigenvalue decomposition of the m×m matrix H*and undo exponential transformation.A3.Structural sensitivity:Computer δλ（x，y）=|^v||^u|^v·^u

1.Theofilis V.Global linear instability.Annu Rev Fluid Mech2011;43:319–52.

2.Gómez F,Clainche SL,Paredes P,Hermanns M,Theofilis V.Four decades of studying global linear instability:progress and challenges.AIAA J2012;50(12):2731–43.

3.Palacios F,Colonno MR,Aranake AC,Campos A,Copeland SR,Economon TD,et al.Stanford University unstructured(SU2):An open-source integrated computational environment for multiphysics simulation and design.Reston:AIAA;2013.Report No.:AIAA-2013-0287.

4.Fischer PF.An overlapping schwarz method for spectral element solution of the incompressible Navier–Stokes equations.J Comput Phys1997;133(1):84–101.

5.Vos PE,Sherwin SJ,Kirby RM.Fromhtopefficiently:Implementing finite and spectralhpelement methods to achieve optimal performance for low-and high-order discretisations.J Comput Phys2010;229(13):5161–81.

6.Cantwell C,Sherwin S,Kirby R,Kelly P.Fromhtopefficiently:Strategy selection for operator evaluation on hexahedral and tetrahedral elements.Comput Fluids2011;43(1):23–8.

7.Weller HG,Tabor G,Jasak H,Fureby C.A tensorial approach to computational continuum mechanics using object-oriented techniques.Comput Phys1998;12(6):620–31.

8.Tezuka A,Suzuki K.Three-dimensional global linear stability analysis of flow around a spheroid.AIAA J2006;44(8):1697–708.

9.Bagheri S,Schlatter P,Schmid PJ,Henningson DS.Global stability of a jet in crossflow.J Fluid Mech2009;624:33–44.

10.Gómez F,Gómez R,Theofilis V.On three-dimensional global linear instability analysis of flows with standard aerodynamics codes.Aerosp Sci Technol2014;32(1):223–34.

11.Theofilis V.Advances in global linear instability analysis of nonparallel and three-dimensional flows.Prog Aerosp Sci2003;39(4):249–315.

12.Schmid PJ,Henningson DS.Stability and transition in shear flows.New York:Springer;2012.p.55–8.

13.Theo filis V.Numerical experiments on the stability of leading edge boundary layer flow:a two-dimensional linear study.Int J Numer Methods Fluids1993;16(2):153–70.

14.Pitt R,Sherwin S,Theo filis V.Biglobal stability analysis of steady flow in constricted channel geometries.Int J Numer Methods Fluids2005;47(10–11):1229–35.

15.Gonza´lez L,Theo filis V,Sherwin S.High-order methods for the numerical solution of the biglobal linear stability eigenvalue problem in complex geometries.Int J Numer Methods Fluids2011;65(8):923–52.

16.Obrist D,Schmid PJ.On the linear stability of swept attachmentline boundary layer flow.Part 2.Non-modal effects and receptivity.J Fluid Mech2003;493:31–58.

17.Tumin A,Wang X,Zhong X.Direct numerical simulation and the theory of receptivity in a hypersonic boundary layer.Phys Fluids2007;19(1):014101.

18.Barkley D,Blackburn HM,Sherwin SJ.Direct optimal growth analysis for timesteppers.Int J Numer Methods Fluids2008;57(9):1435–58.

19.Blackburn HM,Barkley D,Sherwin SJ.Convective instability and transient growth in flow over a backward-facing step.J Fluid Mech2008;603:271–304.

20.Blackburn HM,Sherwin SJ,Barkley D.Convective instability and transient growth in steady and pulsatile stenotic flows.J Fluid Mech2008;607:267–77.

21.Cantwell CD,Barkley D,Blackburn HM.Transient growth analysis of flow through a sudden expansion in a circular pipe.Phys Fluids2010;22:034101-1–034101-15.

22.Hill D.A theoretical approach for analyzing the re-stabilization of wakes.Reston:AIAA;1992.Report No.:AIAA-1992-0067.

23.。Akervik E,Hoepffner J,Ehrenstein U,Henningson DS.Optimal growth,model reduction and control in a separated boundarylayer flow using global modes.J Fluid Mech2007;579:305–14.

24.Henningson DS,。Akervik E.The use of global modes to understand transition and perform flow control.Phys Fluids2008;20(3):031302-1–031302-15.

25.Giannetti F,Luchini P.Structural sensitivity of the first instability of the cylinder wake.J Fluid Mech2007;581:167–97.

26.Nichols JW,Lele S.Global modes and transient response of a cold supersonic jet.J Fluid Mech2011;669:225–41.

27.Fosas de Pando M,Schmid PJ,Sipp D.A global analysis of tonal noise in flows around aerofoils.J Fluid Mech2014;754:5–38.

28.Fosas de Pando M,Sipp D,Schmid PJ.Efficient evaluation of the direct and adjoint linearized dynamics from compressible flow solvers.J Comput Phys2012;231(23):7739–55.

29.Alizard F,Robinet JC,Gloerfelt X.A domain decomposition matrix-free method for global linear instability.Comput Fluids2012;66:63–84.

30.Browne OM,Rubio G,Ferrer E,Valero E.Sensitivity analysis to unsteady perturbations of complex flows:a discrete approach.Int J Numer Methods Fluids2014;76(12):1088–10.

31.Ferrer E,Vicente J,Valero E.Low cost 3d global instability analysis and flow sensitivity based on dynamic mode decomposition and high-order numerical tools.Int J Numer Methods Fluids2014;76(3):169–84.

32.Peplinski A,Schlatter P,Fischer P,Henningson D.Stability tools for the spectral-element code nek5000:application to jet-incrossflow.Spectral and high order methods for partial differential equations.ICOSAHOM 2012,lecture notes in computational science and engineering.2012.p.349–59.

33.Sanmiguel-Rojas E,Jimenez-Gonzalez J,Bohorquez P,Pawlak G,Martı´nez-Baza´n C.Effect of base cavities on the stability of the wake behind slender blunt-based axisymmetric bodies.Phys Fluids2011;23:114103-1–114103-11.

34.Bohorquez P,Sanmiguel-Rojas E,Sevilla A,Jimenez-Gonzalez J,Martinez-Bazan C.Stability and dynamics of the laminar wake past a slender blunt-based axisymmetric body.J Fluid Mech2011;676:110–44.

35.Bohorquez P,Parras L.Three-dimensional numerical simulation of the wake flow of an afterbody at subsonic speeds.Theor Comput Fluid Dyn2012;27(1–2):201–18.

36.Jiménez-Gonza´lez J,Sevilla A,Sanmiguel-Rojas E,Mart´ınez-Baz´an C.Global stability analysis of the axisymmetric wake past a spinning bullet-shaped body.J Fluid Mech2014;748:302–27.

37.Strykowski P,Sreenivasan K.On the formation and suppression of vortex shedding at low Reynolds number.J Fluid Mech1990;218:71–107.

38.Golub GH,van Loan CF.Matrix computations.3rd ed.London:The Johns Hopkins University Press;1996.p.320-9.

39.Morse PM,Feshbach H.Methods of theoretical physics.Part I.New York:McGraw-Hill;1953.p.791–801.

40.Tuckerman L,Barkley D.Bifurcation analysis for timesteppers.In:Doedel E,Tuckerman L,editors.Numerical methods for bifurcation problems and large-scale dynamical systems.New York:Springer;2000.p.443–66.

41.Ferziger JH,Peric M.Computational methods for fluid dynamics.Berlin:Springer;2002.p.71–89.

42.Issa R.Solution of the implicitly discretized fluid flow equations by operator-splitting.J Comput Phys1986;62(1):40–65.

43.Jasak H.Error analysis and estimation for the finite volume method and applications to fluid flows[dissertation].London:Imperial College;1996.

44.Theofilis V.On steady-state flow solutions and their nonparallel global linear instability.In:Dopazo C,editor.8th European turbulence conference.2000.p.35–8.

45.Gómez F,Hermida J,Gómez R,Theofilis V,Carmo BS,Meneguini JR.Three-dimensional transition of the flow past a cylinder fitted with helical strakes.Instability and control of massively separated flows.Switzerland:Springer International Publishing;2015.p.111–6.

46.Barkley D.Linear analysis of the cylinder wake mean flow.Europhys Lett2006;75(5):750–6.

47.Rossiter J.Three-dimensional instability over a rectangular open cavity:from linear stabilty analysis to experimentation.London:Aeronautical Research Council;1964.Report No.:3438.

48.Richardson LF.The approximate arithmetical solution by finite differences of physical problems involving differential equations with an application to the stresses in a masonry dam.Philos Trans R Soc A1911;210:459–70.

49.Roache PD.Perspective:a method for uniform reporting of grid refinement studies.J Fluids Eng1994;116(3):405–13.

50.de Vicente J,Basley J,Meseguer-Garrido F,Soria J,Theofilis V.Three-dimensional instability over a rectangular open cavity:from linear stabilty analysisto experimentation.JFluidMech2014;748:189–220.

51.Brés GA,Colonius T.Three-dimensional instability in compressible flow over open cavity.J Fluids Mech2008;599:309–39.

52.Sarohia V.Experimental investigation of oscillations in flow over shallow cavities.AIAA J1977;15(7):984–91.

53.Rockwell D,Naudascher A.Review-self-sustaining oscillations of flow past cavities.J Fluids Eng1978;100(2):152–65.

54.Rowley CW,Colonius T,Basu AJ.On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities.J Fluid Mech2002;455:315–46.

55.Liberzon A,Feldman Y,Gelfgat AY.Experimental observation of the steady-oscillatory transition in a cubic lid-driven cavity.Phys Fluids2011;23(8):23–32.

56.Giannetti F,Luchini P,Marino L.Linear stability analysis of three-dimensional lid-driven cavity flow.Atti del XIX CongressoAIMETA di Meccanica Teorica e Applicata.2009.p.738.1–738.10.

57.Chomaz JM.Global instabilities in spatially developing flows:non-normality and nonlinearity.AnnuRevFluidMech2005;37:357–92.

13 April 2015;revised 20 May 2015;accepted 21 June 2015

Available online 5 March 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+34 91 336 32 98.

E-mail address:liuqiong.upm@gmail.com(Q.Liu).

Peer review under responsibility of Editorial Committee of CJA.

Liu Qiongis a Ph.D.candidate of Computational Fluid Mechanics Unit at the Universidad Politécnica de Madrid.Her research interests include flow stability,adjoint-based flow control as well as laminarturbulent transition.