Numerical simulations of high enthalpy flows around entry bodies

Cai Chunpei

Department of Mechanical Engineering-Engineering Mechanics,Michigan Technological University,Houghton,MI 49931,USA

Numerical simulations of high enthalpy flows around entry bodies

Cai Chunpei*

Department of Mechanical Engineering-Engineering Mechanics,Michigan Technological University,Houghton,MI 49931,USA

Chemical reactions;Compressible flows;Fluid dynamics;Finite volume methods;Hypersonic flow;Navier–Stokes equations;Numerical method

Ablation flows around entry bodies are at highly nonequilibrium states.This paper presents comprehensive computational fluid dynamics simulations of such hypersonic flow examples.The computational scheme adopted in this study is based on the Navier–Stokes equations,and it is capable of simulating multiple-dimensional,non-equilibrium,chemically reacting gas flows with multiple species.Finite rate chemical reactions,multiple temperature relaxation processes,and ionizations phenomena with electrons are modeled.Simulation results of several hypersonic gas flows over axisymmetric bodies are presented and compared with results in the literature.It confirms that some past treatment of adopting less species for hypersonic flows is acceptable,and the differences from more species and more chemical reactions are not significant.

1.Introduction

Thermal protection systems(TPSs)are essential for the successful operation of space vehicles.1Simulating the hypersonic ablation flows around a TPS system involves many challenges which include,but not limited to,multiple species with chemicalreactionsand complex thermodynamicsrelations,2,3mechanical ablation,4thin shock waves with large gradients and interactions with boundary layers,multiple dimensions with possible surface recessions,multiple temperatures,radiations,and other multiple physics demanding careful modellings.Investigations with experiments are expensive and challenging;hence,we usually rely on computational fluid dynamics(CFD)simulations to investigate these flows.

In the literature,there are many investigations on hypersonic flows,and only some of them are listed here.Some concentrated on numerical scheme development and parameter effects.5,6Some adopted particle simulation methods,such as the direct simulation Monte Carlo(DSMC),which are quite flexible for rare fied hypersonic flows.7–10Zhong et al.8included 11 species and 31 reactions.Much other works during the past adopted the Navier–Stokes equations(NSEs).Gosse and Candler2modeled the gas flow over a sphere-cone vehicle coupling in the solution of the mass and energy balance with surface reactions at an altitude of 16 km.In that work,gas–surface reactions and surface sublimation were included,and it was found that the predicted surface recession rate for a validation case was lower than that from experimental measurement.Chen and Milos11studied a hypersonic flowfield over a dense carbon-phenolic heat shield under flow conditions typical forearth reentry from a plant-entry mission.The ablation surface conditions of oxidation irradiation and material sublimation were coupled with NSEs and it was found that the surface ablation had only a small impact on the predicted convective heat flux.Huang12concentrated on silicon-based materials,and it was found that the effects from resin materials on the ablation flowfield were appreciable.

This paper presents some hypersonic flow simulations with an NSE-based CFD solver which can serve as a foundation for further development.The next few sections are organized as follows:in Section 2,some details for the governing equations and numerical schemes are presented;in Section 3,some detailed thermodynamics relations and chemical reaction models are listed,Section 4 includes some simulation results with comparisons and discussions,and Section 5 draws several conclusions.

2.Governing equations and numerical schemes

The new CFD solver is based on NSEs.The axis-symmetric NSEs are listed as follows,including some chemical reaction source terms13:

where ‘‘in” and ‘‘v” represent inviscid and viscous properties;subscripts ‘‘x”and ‘‘r” represent partial derivatives along thexandrdirections;andGvis one source term related to axissymmetry:

whereuandvare the velocity components along thex-andrdirections,ρ is the mixture density,ρiis the density for theith species,pis the mixture gas pressure,Eis the mixture total internal energy,evthe specific vibrational energy,Dthe diffusion coef ficient,Xthe species concentration,nsthe number of species,ω·the source terms for density,andSvthe source term for vibrational energy.The shear stress tensor τ and the heat fluxqare:

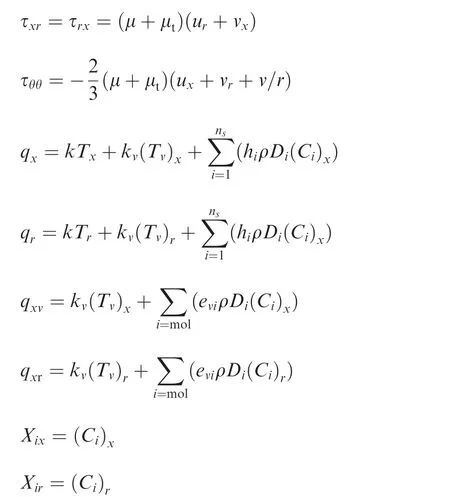
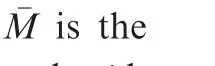
Before solving Eq.(1),they are non-dimensionalized,and the coordinate system is mapped into a curvilinear system.For in-viscid flux computation,the coefficient matrix needs to be computed and decomposed into an eigenvalue matrix.The Sterge flux scheme is used to compute the fluxes,and the properties at the cell edge are computed with the Roe scheme.14,15

Once the fluxes across the cell interface are obtained,the source termWfor chemical reaction and vibrational energy relaxation is evaluated.By solving a set of ordinary differential equations(ODEs),dWi/dt=Si,we can update the flowfield properties with these source term contributions.In summary,an update of the flowfield properties from time stepnton+1 is obtained by the following equation:

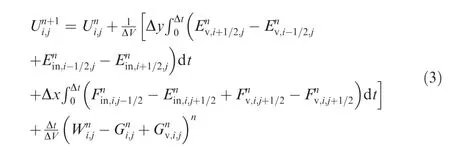
whereUni，jare the flow properties for cell(i,j)at momentT=nΔt;Ei+1/2，jare the fluxes across the cell interfacei+1/2 along thex-direction,andFi，j+1/2along they-direction in the same manner asEi;Wni，jare the chemical reaction sources in cell(i,j)with a cell volume ΔV.

3.Thermodynamics for hot gas and chemical reaction modeling

For the development of this CFD solver,the chemical reactions are crucial,and much efforts have been spent upon them.There are many curve-fitting results,which are critical for successful simulations of hypersonic flows;one good reference is by Park.16

3.1.Thermodynamics models for single species hot gas

The mole specific internal energy and mole specific heat energy at a constant volume for the mixture are computed with different models,and the formulas for monatomic,diatomic,and linear and non-liner polyatomic molecules are different.17For example,the formulas for non-linear polyatomic molecules are:

wherenis the number of atoms inside the non-linear polyatomic species,and Θvlthe characteristic vibrational temperature for thelth polyatomic species.

In this work,the viscosity coefficient for theith species,μi,is obtained by curve-fitting:

whereai,bi,andciare the curve-fitting results18for theith species,andTkis the local temperature.

For theith species,the thermal conductivity,ki,and the vibrational energy thermal conductivity,kvi,are given by Eucken’s empirical formulas19:

whereCpiandCviare the constant pressure specific translational energy and constant volume specific translational energy,respectively.

3.2.Thermal properties for gas mixture

The bulk viscosity coefficient μ and the conductivity coeff icientsk,kvfor the mixtures are given by Wilke20:

3.3.Chemical reaction source term computations

For a chemical reaction system withnsspecies andnrreactions,the general form of therth reaction equation can be written as21:

One possible method to calculate the energy source term is:

which is the summation of the rate of change times the formation heat of each species,where ω·iis the generation rate for theith species.

The forward and backward reaction rates for therth reaction are denoted as

whereTis the temperature of the reaction.C0r,C1r,C2r,D0r,D1r,andD2rare constants related to the reaction.

If the mole density for theith species is denoted as[Xi]andCi= ρi/ρ is the mass fraction for theith species,then there is a relation:

For theith species that is involved in the reactions,we can define:

The combination and dissociation reactions may involve third-body collisions.A third body which is denoted asMcan be any molecules,atoms,or radicals inside the reaction system,and the efficiencies of different third-bodies may vary.Usually,a third-body in a certain reaction is treated as one ordinary species,and the contributions of all possible thirdbodies to the mole fraction should be considered.Let’s denote the third-body efficiency of speciesjwith the third-body numberiasZij;then,the mole fraction of this third-body should be modified as follows:

The mass change rate of theith species is calculated as:

Therefore,the rate of change of[Xi]in therth reaction is given as17:

wherenjis the number of species plus the number of third bodies.

A combination of the above relations leads to:

In the above equation,the following four notations are introduced:

The creation rate for therth reaction is:

The net mass creation rate for theith species is calculated by summing up all reactions as follows:

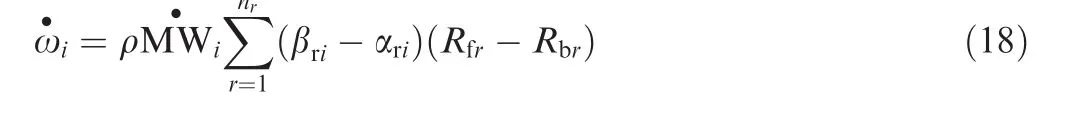
3.4.Vibration–dissociation coupling model

For nonequilibrium flows,the dissociation and vibrational energy relaxation have similar behaviors.17In this work,the bi-temperature model by Park is adopted to describe the air dissociation process and the vibrational energy relaxation.

The above formula is empirical,but it is the most widely adopted model and the results are quite satisfying.In this work,mf=0.5 andnf=0.5.

3.5.Vibrational–dissociation reaction modeling

At a thermochemical non-equilibrium state,the characteristic dissociation time scale for air and that for the vibrational energy relaxation time scale are comparable,and the interactions between them can be described with a vibration–dissociation(V–D)coupling model.The bi-temperature model by Park22is used:

The results from this simple model are satisfying,and in general,mandnare set to 0.5.It shall be mentioned that in the literature,it was argued that for high enthalpy flows,mfshall be taken as 0.7 andnfas 0.3.

3.6.Vibrational energy relaxation model

The vibrational energy source termSvforWin Eq.(1)is:

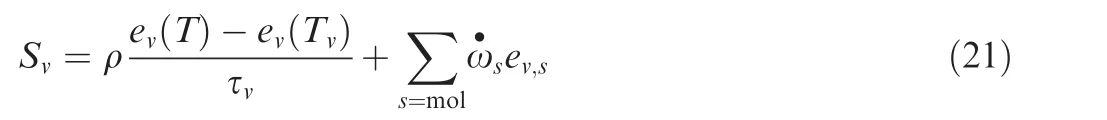
whereev(T)is the vibrational energy computed by using the equilibrium translational temperature,ev(Tv)is the vibrational energy computed with the vibrational temperature,and τvis the characteristic vibrational temperature relaxation time scale.For a temperature between 3000 K and 8000 K,Milikan and White23provided a formula for the relaxation time for thesth species:

whereMij=MiMj/(Mi+Mj),njis the number density for thejth species,and the unit for pressurePis atm.

For a temperature over 8000 K,Park22offered some corrections for the relaxation time scale:

3.7.Ablation boundary conditions

A new reaction model for a TPS with silicon-related materials is developed.The silica–carbon reaction is

To compute the reaction rate,the reaction temperature needs to be determined,which is defined as

wherepeis the pressure of the gas environment.The mass flow rate of the gaseous product in Eq.(25)is modeled as

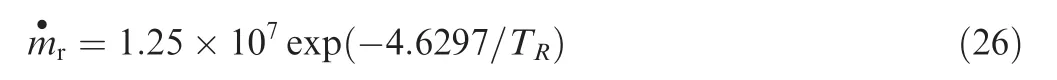
The mass flow rate of the silicon material is given by

wherem·wis the total mass flow rate injected to the flow field,m·tis the total mass loss rate of the TPS,and ε is the fraction ofm·wtom·t.

4.Validations and discussions

To validate the above numerical scheme,the above scheme is incorporated into an in–house software package GRASP24as a new module,and three cases are simulated,all of which are about non-equilibrium flows over an axisymmetric body.The free stream flow is assumed as pure air.

For the first test case,the simulation parameters and geometry profiles are set to the same as those used by Candler25:the blunted body radius is set toRn=6.35 mm;the free stream Mach number isMa∞=15.3 (orV∞=5280 m/s);T∞=293 K andp∞=664 Pa.In the past,Candler25adopted a model of 7-species and 7-reactions and Coquel26adopted a model of 5-species and 5-reactions.In this work,a model of 11-species and 20-reactions is used;this model was proposed by Gupta and Yosn.27

Fig.1 compares the results from this work and those by Candler.25The free stream flow is set from the right to the left.In this figure,TandTvrepresent the translational and vibrational temperatures.Fig.1(a)shows the temperature profile along the central stagnation line,while Fig.1(b)shows the ratio of major species mass concentrations of(O,N,O2,N2,NO)along the same stagnation line.As shown,the translational and vibrational temperatures from the simulations in this work and those by Candler have quite close peak values.The corresponding positions for the peak temperature values are close as well,and the mass concentrations along the stagnation line are close.There are appreciable differences between the mass concentration values for N2and O2due to different given free stream values.Behind the shock wave,in general,our simulation results of mass concentrations(O,N,and NO)agree well with Candler’s results.25The minor differences may come from different chemical reaction models.

Fig.2 illustrates some comparisons with Coquel’s results.26Fig.2(a)is for the temperature results along the stagnation line,while Fig.2(b)the mass concentrations for major species O,N,O2,N2,and NO.As can be seen from these two figures,the translational temperature profiles have quite similar positions while there are appreciable differences between the highest values.The past work by Coquel26presents slightly larger peak values.There are relatively larger differences in the highest vibrational temperatures.The mass concentrations along the stagnation line agree quite well.The free stream flows have the same conditions for N2and O2,while behind the shock wave,atoms O,N,NO and molecules N2,O2have agreement in the mass concentrations.The minor differences are due to the different chemical reaction models.The simulation results from this test case indicate that the physical modeling and the numerical scheme for the NSEs in this work are both reliable;hence,we can proceed to investigate more complex high temperature ablation flows with multiple species and chemical reactions.

For the second test case,high speed flows over an axisymmetric blunted body are simulated by adopting models with different numbers of species,and the flowfield results are compared.The simulation geometry is available in the literature.12Ablative boundary conditions were applied to simulate the ablation due to the high speed flow.The results of pure air flow(without ablations)and those with ablations are compared.For simulations of this type of high speed flows,accurate chemical models for charge exchanges can directly affect the accuracy of electron number density28,29and several other interesting flowfield properties.Based on thework by Cresswell and Porter30,a 26-species model with 54 chemical reactions was developed which considered resin with siliconrelated species.Bortner31proposed a widely accepted and relatively accurate chemical reaction model in 1966.In the eighties,Parker22summarized the past works on chemical reactions, and proposed some curve-fitting formulas.Resin-based materials which are related with silicon,such as Si,SiO,and SiO2,are considered for the simulations.Ions and electrons are also included in the modeling and the flowfield results are quite comprehensive.In this simulation,a model of 19 species and 34 simplified chemical reactions is considered,and to keep this paper concise,detailed chemical reactions are not provided here.The free stream air flow is set toU∞=5000 m/s and the flight heightH=50 km.Electron densities are set to the same as the ion number densities by using the quasi-neutral charge condition in plasma.Fig.3(a)and(b)presents the translational and vibrational temperature contours.One set of results includes the ablation effects on the blunted surface,while the others do not.By considering the ablation effects,the translational and vibrational temperature values are significantly smaller than the corresponding values in the case without ablations.These results indicate that the thermal protection system is quite effective.It is evident that the 19-species model can capture the flowfield with quite high accuracy.Fig.3(c)and(d)shows the ablation effects on the pressure field and the electron number density.They illustrate that the shock standing off distance is much larger in the situation of considering the ablation effects,probably due to more out-gassing into the main flowfield.Meanwhile,the electron number density is much higher for the ablation flow situation,probably because the surface ablations create larger gas density,and hence higher collision rates.

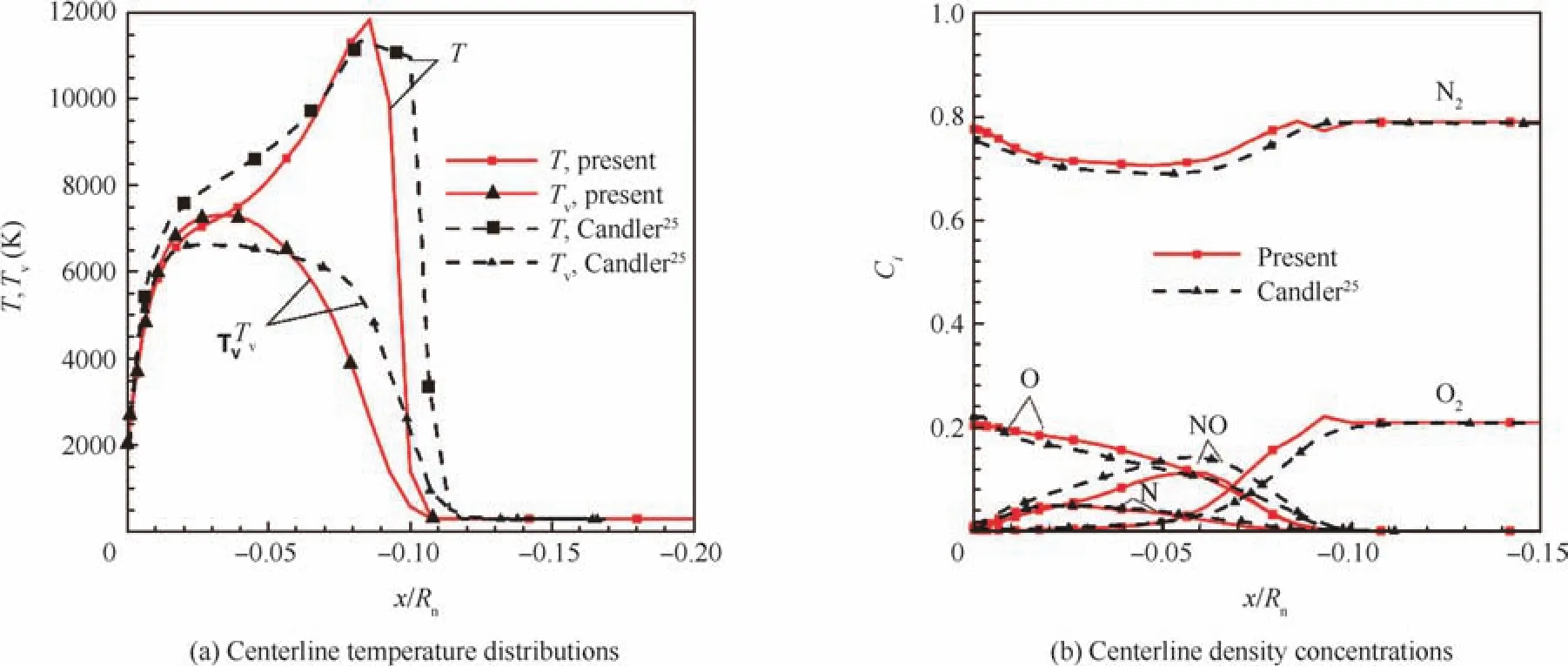
Fig.1 An 11-species and 20-reactions model,current vs Candler’s results.25

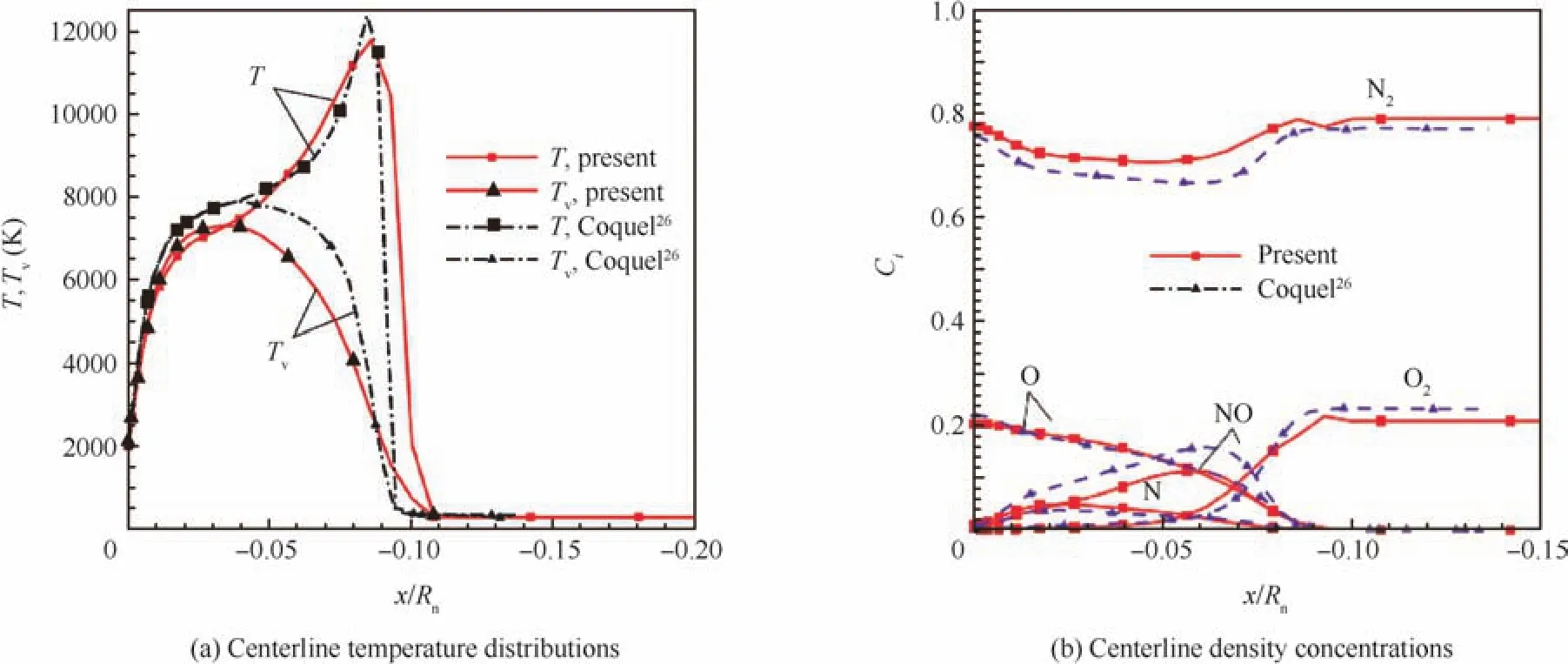
Fig.2 An 11-species and 20-reactions model,current vs Coquel’s results.26

Fig.3 A 19-species and 26-reactions model,U∞=5000 km/s,altitude 50 km.

The last test case is about hypersonic flows over an axisymmetric double-cone geometry with flow separations at the cone shoulder.The con figuration has a first cone of a half-angle of 25°,and the second cone 55°.Detailed geometry pro files are available in the literature.32Under the experimental condition(RUN 28)33,the incident flow has the following parameters:ρ∞=0.6545 × 10-3kg/m3，U∞=2664.00 m/s，T∞=185.56 KT∞=293.33 K，Ma∞=9.59，Re=13090

The RUN 28 with the above flow condition is the most difficult one to be calculated due to the large flow separation region.The first cone produces an attached shock wave,and the second cone with a large angle produces one detached bow shock.The two shocks interact to form a transmitted shock that strikes the second cone surface over the cone–cone junction.The adverse pressure gradient due to the cone junction and the transmitted shock generate a large region of the separated flow that produces its own separation shock.This shock interacts with the attached shock from the first,altering the interaction with the detached shock from the second cone.This in turn affects the size of the separation region.The shock interaction produces very high surface pressure and heat transfer rates where the transmitted shock impinges on the second cone.

Fig.4 A 20-species model.

In the literature,there are many CFD simulations,for example,Xu et al.32provided detailed flow patterns.Most of them used pure air assumptions without considerations of chemical reactions.In this work,the flowfield is simulated with two scenarios,aiming to investigate the chemical reaction effects on the flowfield.One simulation adopts pure air of two species,O2and N2,and no chemical reactions;this corresponds to a frozen flow situation.The other simulation adopts 20 species and 26 chemical reactions,with different finite rate chemical reactions,and for simplicity,the details for these equations are omitted here.Fig.4(a)compares the surface pressure distributionsCp,and Fig.4(b)shows the corresponding surface heat coefficientsCq.Lis the base cone length.As can be seen,only minor differences exist between the two sets of simulation results,and it can be concluded that a consideration of multiple species actually only creates minor effects on the surface properties.Fig.4(c)and(d)shows the pressure and temperature field results from the two simulations.As can be seen from these two figures,the shock–shock interactions and other flow field patterns are well captured.While the simulation with a consideration of chemical reactions yields slightly minor differences in the temperature field,the pressure field is almost identical.

5.Conclusions

This paper presented some work on simulating high speed chemically reacting complex flows with multiple species,with a newly developed NSEs-based CFD solver.Chemical reactions with multi-species,multi-dimensions,and structured mesh are adopted to ensure high accuracy for the simulations.Three benchmark test cases are simulated and compared.For the first test case,some simulation results along the stagnation line were compared with past results in the literature,and acceptable agreements are observed.For the second test case,a model of 19-species was adopted,and a consideration of surface ablation yields a much cooler flowfield and a larger shock standing off distance-probably due to the mass release into the flowfield and energy absorption during the ablation.For the third test case,considerations of multiple species and finite rate chemical reactions actually do not yield appreciable differences from the case of pure air flow without chemical reaction.There were many CFD simulations in the past and the chemical reactions were neglected—our simulation results confirmed that this treatment was appropriate.

These simulation results indicate that the simulation solver has good fidelity.The multi-species model for the test cases is suf ficient to capture some fundamental flow field features.Some minor differences can be observed.Including these finite rate chemical reactions,internal energy relaxations,and even ionization allows us to incorporate more physics.There are also many CFD simulations in the literature which neglected the chemical reactions completely—it is a frozen flow assumption.Such treatments can conveniently be achieved by simply switching off some options in this new CFD solver;as such,this solver is quite comprehensive.It may offer us fast baseline estimations without chemical reactions,and it is also feasible to add new chemical reaction models to improve current ones.Hence,it is a reliable platform for further development.

1.Covington MA,Heinmann JM,Goldsten HE.Performance of a low density ablative heat shield material.Reston:AIAA;2004.Report No.:AIAA-2004-2273.

2.Gosse R,Candler G.Ablation modeling of electro-magnetic lunched projectile for access to space.Reston:AIAA;2007.Report No.:AIAA-2007-1210.

3.Suzuki T,Furudate M,Sawada L.Unified calculation of hypersonic flowfield for a reentry vehicle.J Thermophys Heat Transfer2002;16(1):94–100.

4.Palaniathan R,Bindu S.Modeling of mechanical ablation in thermal protection system.J Spacecraft Rockets2005;42(6):971–9.

5.Ma Y,Zhong X.Receptivity of a supersonic boundary layer over a flat plate,Part 3:Effect of different free stream disturbances.J Fluid Mech2005;532:63–109.

6.Ma Y,Zhong X.Receptivity of a supersonic boundary layer over a flat plate,Part 1:Wave structures and interactions.J Fluid Mech2003;488:31–78.

7.Bird GA.Molecular gasdynamics and numerical simulation methods.1st ed.New York:Oxford University Press;1994.

8.Zhong JQ,Ozawa T,Levin D.Comparison of high-altitude hypersonic wake flows of slender and blunt bodies.AIAA J2008;46(1):251–62.

9.Zhong JQ,Ozawa T,Levin DA.Modeling of stardust reentry ablation flows in the near-continuum flight regimes.AIAA J2008;46(10):2568–81.

10.Boyd ID,Zhong JQ,Levin D,Jenniskens P.Flow and radiation analysis for stardust entry at high altitude.Reston:AIAA;2008.Report No.:AIAA-2008-1215.

11.Chen YK,Milos FS.Navier-Stokes solutions with finite rate ablation for planetary mission earth reentries.J Spacecraft Rocket2005;42(6):961–70.

12.Huang X.Numerical studies on the ablation flows around blunted bodies of resin materials[dissertation].Beijing:Institute of Mechanics,Chinese Academy of Sciences;2008.

13.Anderson JD.Hypersonic and high temperature gas dynamics.2nd ed.Virginia:AIAA Education Series,AIAA Inc.;2006.

14.Roe P.Approximate Riemann solvers,parameter vectors,and difference schemes.J Comput Phys1981;43(2):357–72.

15.Hirsch C.Numericalcomputationofinternalandexternal flows.New Jersey:Wiley and Sons;2002.p.137–42.

16.Park C.Nonequilibrium hypersonic aerothermodynamics.New Jersey:Wiley and Sons;1990,p.99–102.

17.Vincenti WG,Kruger CH.Introduction to physical gas dynamics.Malabar,Florida:Krieger Publishing;1975.p.122–38.

18.Blottner F,Johnson M,Ellis M.Chemically reacting viscous flow program for multi-component gas mixture.Albuquerque(NM):Sandia Lab;1971.Report No.:SC-RR-70-754.

19.Eucken A.Allgemeine gesetzma¨βigkeiten,fu¨r das wu¨rmeleitvermo¨gen verschiedener stoffarten und aggregatzusta¨nde.Forschung Gabiete Ingenieur1940;11(1):6–20.

20.Wilke CR.A viscosity equation for gas mixtures.J Chem Phys1950;18(4):517–9.

21.Turns S.An introduction to combustion:concepts and applications.2nd ed.Columbus,OH:McGraw Hill;2010.p.228–31.

22.Park C.Problem of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles.Prog Astronaut Aeronaut1985;96:511–37.

23.Milikan RC,White DR.Systematics of vibrational relaxation.J Chem Phys1963;39(12):3029–213.

24.Liu H,Cai C,Zou C.An object-oriented implementation of the DSMC method.Comput Fluids2012;57:65–75.

25.Candler G.The computation of weakly ionized hypersonic flows in thermo-chemical nonequilibrium[dissertation].Stanford(CA):Stanford University;1998.

26.Coquel F,Flament C.Viscous nonequilibrium flow calculations.9th ed.Boston:Birkhauser;1992.p.299.

27.Gupta R,Yosn J.A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30000 Kel.Washington,D.C.:NASA;1990.Report No.:NASA Internal Note 1232.

28.Starkey RP.Electromagnetic wave/magneto-active plasma sheathe interaction for hypersonic vehicle telemetry blackout analysis.Reston:AIAA;2003.Report No.:AIAA-2003-4167.

29.Mather DE,Pasqual JM,Sillence JP.Radio frequency(RF)blackout during hypersonic reentry.Reston:AIAA;2005.Report No.:AIAA-2005-3443.

30.Cresswell K,Porter B.Material effects of low temperature ablators on hypersonic wave properties of slender bodies[Internet].TIS67SD255,General Electric Co.,Internal Report;1967.

31.Bortner MH.Suggested standard chemical kinetics for flow field calculations–a consensus opinion14th AMRAC proceeding,institute scientific and technology Report.Michigan:University of Michigan;1966.p.569–81.

32.Xu K,Mao M,Tang L.A multi-dimensional gas-kinetic BGK scheme for hypersonic viscous flow.J Comput Phys2005;203(10):405–21.

33.Holden MS,Wadhams TP.A review of experimental studies for DSMC and Navier–Stokes code validation in Laminar regions of shock/shock and shock boundary layer interaction including gas effects in hyper-velocity flows.Reston:AIAA;2003.Report No.:AIAA-2003-3641.

12 May 2015;revised 28 July 2015;accepted 21 September 2015

Available online 24 February 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Tel.:+1 575 9155687.

E-mail address:ccai@mtu.edu.

Peer review under responsibility of Editorial Committee of CJA.

Cai Chunpeiis an associate professor and Ph.D.advisor in the Department of Mechanical Engineering-Engineering Mechanics at Michigan Technological University in Houghton,USA.He received his B.E.degree in naval architecture from Harbin Engineering University in 1994,M.S.degree in fluid mechanics from the Institute of Mechanics at Chinese Academy of Sciences in 1997,M.S.degree in mechanical engineering from Cornell University in 1999,and Ph.D.degree in aerospace engineering from University of Michigan in 2005.His research area includes nonequilibrium gasdynamics,plasma flows,space engineering,and computational fluid dynamics.