Modeling and simulation of a time-varying inertia aircraft in aerial refueling

Wang Haitao,Dong Xinmin,Xue Jianping,Liu Jiaolong,Wang Jian

Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China

Modeling and simulation of a time-varying inertia aircraft in aerial refueling

Wang Haitao,Dong Xinmin*,Xue Jianping,Liu Jiaolong,Wang Jian

Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China

Aerial refueling;Equations of motion;Hose–drogue assembly;Time-varying inertia;Whipping phenomenon

Studied in this paper is dynamic modeling and simulation application of the receiver aircraft with the time-varying mass and inertia property in an integrated simulation environment which includes two other significant factors,i.e.,a hose–drogue assembly dynamic model with the variable-length property and the wind effect due to the tanker’s trailing vortices.By extending equations of motion of a fixed weight aircraft derived by Lewis et al.,a new set of equations of motion for a receiver in aerial refueling is derived.The equations include the time-varying mass and inertia property due to fuel transfer and the fuel consumption by engines,and the fuel tanks have a rectangle shape rather than a mass point.They are derived in terms of the translational and rotational position and velocity of the receiver with respect to an inertial reference frame.A linear quadratic regulator(LQR)controller is designed based on a group of linearized equations under the initial receiver mass condition.The equations of motion of the receiver with a LQR controller are implemented in the integrated simulation environment for autonomous approaching and station-keeping of the receiver in simulations.

1.Introduction

Air to air refueling is an effective method of increasing the endurance and range of aircraft.Most recently,there has been increasing interest in autonomous aerial refueling(AAR)for the continuing research into unmanned aerial systems.Over the last decade,there have been a wealth of research and academic publications on the theoretical and practical aspects of automating the refueling process covering aircraft control,sensor systems,and their integration.1–4In order to further develop and evaluate these researches,it is critical to model the whole aerial refueling system with sufficient accuracy,taking into account all major factors including the aircraft,aerodynamic and atmospheric disturbances,and refueling apparatus.For the probe-drogue refueling,three of the most significant factors are the dynamic model of the receiver aircraft with the time-varying mass and inertia property,a hose–drogueassembly(HDA)dynamicmodelwiththe variable-length property and the wind effect due to the tanker’s trailing vortices.

It is generally accepted that it is sufficient to consider the dynamics of an aircraft at a number of fixed,specified,overallweights.5If a mass change is within about 5%of the beginning mass after a period of 60 s,the constant mass assumption is considered acceptable.6Therefore,the research community has put little effort into the investigation of dynamics of systems with inertia variation.However,the mass change of the receiver is up to 18.8%within a period of 60 s in aerial refueling.Under this condition,the effect of the mass change on the dynamics of the aircraft could not be negligible.Earlier aerial refueling studies7,8either ignore the effect of mass transfer completely or treat it as a disturbance causing parametric uncertainty.To develop an accurate dynamic model of the aircraft,Dogan et al.9–11proposed a set of nonlinear,6-DOF equations of motion of a receiver aircraft undergoing aerial refueling.The equations,including the time-varying inertia associated with fuel transfer as well as the vortex-induced wind effect from the tanker,are expressed relative to the tanker and very rigorous from the mathematical perspective.Even so,they have a very complex mathematical expression and seem too complicated to be easily applied to the simulation and analysis.

This paper focuses on the development of the derivation of a simpler aircraft model with the time-varying mass and inertia property.By extending equations of motion of a fixed weight aircraft,5comparing with the ones developed by Dogan et al.,the equations can reflect the time-varying mass and inertia property of an aircraft more factually due to(A)reflecting both the fuel increase and the fuel decrease at the same time(i.e.,the fuel transfer in refueling and the fuel consumption by engines),and(B)the fuel tanks having a rectangle shape rather than a mass point,(C)the equations of motion are derived relative to an inertial frame rather than the tanker body frame,(D)the model has a simpler mathematical expression and is easily applied to the simulation and analysis.Thus,they have a more strong universality.

To validate the proposed aircraft model in an integrated simulation environment for probe-drogue-based autonomous aerial refueling,a dynamic model of the HDA developed by the authors12–16and a dynamic model of the vortex effect in aerial refueling developed by Dogan et al.17–19are also used in the simulation.

2.Equations of motion of a time-varying inertia aircraft

2.1.Equations of motion relative to Earth-centered inertial frame

2.1.1.Definitions of coordinate frames and assumptions

A receiver aircraft often performs long-range,even globestraddling military operations.Under this condition,the effect of the shape and the rotation of the Earth on the dynamics of the receiver aircraft should not be totally omitted.Therefore,without any loss of generality,an Earth-centered inertial(ECI)frame is chosen as an inertial reference frame.Fig.1 shows the ECI frame(Oexeyeze),an aircraft-body coordinate(ABC)frame(Obxbybzb),and an intermediate north-eastdown(NED)frame(Onxnynzn)on the surface of the Earth,5and ωeis the absolute angular velocity vector of Earth’rotation,rnis the position vector of the center of mass of the aircraft inOnxnynzn.

To facilitate the derivation of the dynamics equations including the effect of time-varying inertia,an aircraft-fuel system is considered to comprise two parts as(A)solid,(B)fuel in tanks11as shown in Fig.1.The total amount of mass that occupies the fuel pipes has not been included here.The solid part is considered rigid with constant mass.The origin ofObxbybzbis chosen to be at the center of mass of the solid part,such that the standard definitions of aerodynamic variables and aerodynamic stability derivatives can be directly used without any modification or reinterpretation.5The fuel in fuel tanks is represented bykmasses.The mass of fuel in thejth fuel tank,mj（j=1，2，...，k）,is time varying.The position vector from the center of mass of the fuel to the origin ofObxbybzb,rj,is assumed to be a constant.

2.1.2.Translation kinematics

Taking a derivative of the inertial position vector reof the center of mass of the receiver aircraft inOexeyezeyields5

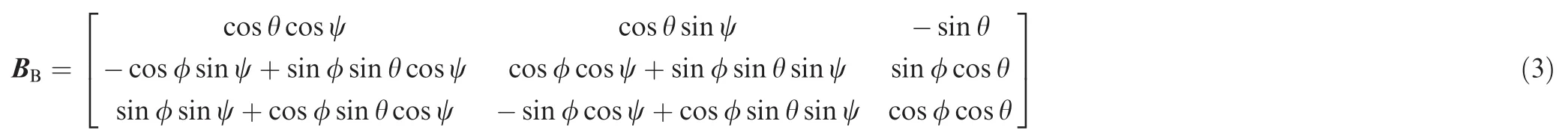
Fig.1 Coordinate frames for modeling.

where ωe× redenotes the absolute velocity of surrounding air at re,B the rotation matrix fromOexeyezetoObxbybzb,BBthe rotation matrix fromOnxnynzntoObxbybzb,Vebthe absolute velocity vector of the aircraft center of mass expressed inObxbybzbrelative toOexeyeze,Vbthe relative velocity vector of the aircraft center of mass expressed inObxbybzbrelative toOexeyeze.φ,θ,ψ are the orientation angles.l,μ are the longitude and latitude.

From Eq.(1),the translational kinematic equation of the aircraft relative toOexeyezecould be expressed as

2.1.3.Translation dynamics

Newton’s law for translational motion of a time-varying inertia aircraft takes the form

where Fbis the vector sum of the aerodynamic and propulsion forces expressed inObxbybzb,mthe overall weights of the aircraft,gethe gravitational acceleration vector measured inOexeyeze.

According to the theorem of Coriolis5,the differentiation of Vbcould be expressed as

where ωbis the absolute angular velocity vector of the aircraft.

It is straightforward to know˙ωe=0.Substituting Eqs.(5)and(7)into Eq.(6)yields

wheremcould be regarded as the sum of the mass of the solid part and the fuel in all tanks and expressed as

wheremsis the mass of the solid part of the receiver.

It is straightforward to know˙ms=0.Thus,˙mcould be expressed as

Substituting Eqs.(1),(9),and(10)into Eq.(8)and rearranging the equation,the translation dynamics equation of a receiver with varying mass relative toOexeyezecould be expressed as

Known from Eq.(11),if the dynamics effects of varying inertia,i.e.,mjand˙mj,are neglected,Eq.(11)will have the same expression as a fixed weight aircraft’s translation dynamics equation.

2.1.4.Rotational kinematics

The rotational kinematical differential equations take the form of Poisson’s equation5

where Ω is the cross-product matrix of the angular rates with respect to the axes of the rotating frame5,that is

wherep,q,rare roll,pitch,and yaw angular rates respectively.

2.1.5.Rotational dynamics

The aerodynamic effects depend on the shape of the receiver aircraft body and the motion of the air relative to the body.Thus,the aerodynamic moments acting on a fixed weight aircraft can be directly used without any modification or reinterpretation here.To simplify the analysis,the thrust vector is aligned alongObxbybzb’sxaxis through the center of mass of the receiver,pointing toward its nose.However,the gravity vector of the fuel in each tank does not act through the center of mass of the receiver due to the tanks’configuration.Thus,the total moment T about the center of mass of the receiver could be expressed as

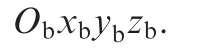
Newton’s law for rotational motion takes the form

where I is the total inertia matrix of the receiver.

According to the theorem of Coriolis,5Eq.(15)could be written as

where I could be regarded as the sum of the inertia matrix of the solid part and the fuel in all tanks,and expressed as follows

where Isis the sum of the inertia matrix of the solid part of the receiver and Ijthe inertia matrix of the fuel in thejth fuel tank.

According to the parallel-axis theorem,Ijcould be written as

where I0jis the inertia matrix of the fuel in thejth fuel tank relative to its own parallel-axis and E the unit matrix.

It is straightforward to know that˙Is=0.Thus,˙I could be expressed as

Substituting Eqs.(14),(17)–(19)into Eq.(16),and rearranging the equation,the rotation dynamics equation of the receiver with varying inertia could be expressed as

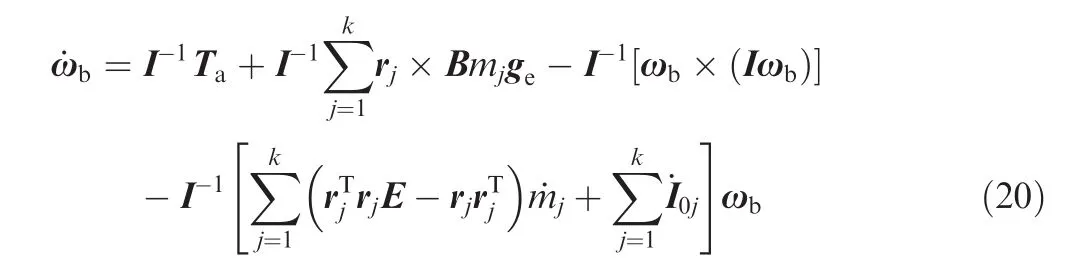
Known from Eq.(20),if the dynamics effects of varying inertia,i.e.,˙mjand˙I0j,are neglected,Eq.(20)will have the same expression as a fixed weight aircraft’s rotation dynamics equation.

2.2.Equations of motion relative to NED frame

For many short range flights,the effect of the shape and the rotation of the Earth on the dynamics of a receiver aircraft could be neglected.Therefore,equations of motion of a time-varying inertia receiver relative to the NED frame are more practical.Assuming ωe=0,replacing B with BB,and replacing gewith g,a reduced set of equations of motion of a time-varying inertia receiver relative to the NED frame is listed as follows:

Navigation equation is

Force equation is

where g is the gravitational acceleration vector measured inOnxnynzn.

Kinematic equation is

Moment equation is

Eq.(23),which consists of 9 coupled differential equations and is highly redundant,could be simplified by two methods.One is three-variable attitude(Euler angles)method commonly used for simulation,and the other is four-variable attitude method suitable for around-the-Earth flight,all-attitude flight and simulation of spinning bodies.

2.3.Fuel tank configuration and fuel consumption

A tailless fighter aircraft with innovative control effectors(ICE)11as the receiver is employed to show how the fuel tanks areincorporated asmathematicalquantities,which are required in the equations of motion.It is assumed that the amount and the location of the tanks,the fuel capacity of each tank,and the fuel flow distribution are set identical to Ref.11.However,each fuel tank has a rectangular shape rather than a lumped mass.Fig.2 shows the sketch of the ICE with 4 fuel tanks and thejth rectangular fuel tank with varying fuel.

For a rectangular fuel tank as shown in Fig.2,I0jin Eq.(18)could be expressed as

Fig.2 Configuration of fuel tanks of ICE.

where the height of the fuelczcould be expressed as a function about the mass of the fuel in thejth tank as

where ρ is the density of the fuel.ax,byare shown in Fig.2.

For the rectangular fuel tank as shown in Fig.2,˙I could be expressed as

The mass of the fuel in the fuel tanks will decrease due to the fuel consumption by engines.Thus,it is assumed that the consumption fuel flow by the engine˙mEcould be expressed as a function about the thrustT:

whereamis the acceleration of the fuel consumption by the engine and η the equivalent coefficient.

2.4.Position-tracking LQR controller for approaching and station-keeping in aerial refueling

To ensure the safety and avoid the core area of the vortexinduced wind field,a reference trajectory is generated by a polynomial fitting curve20through the formation position(FP),the turning position(TP),the pre-docking position(PP),and the drogue position(DP)as shown in Fig.3.

To employ the LQR control,the nonlinear equations of motion of the receiver aircraft relative to the NED frame derived above is trimmed and linearized at the steady level flight condition and initial mass.Linearizing Eqs.(21)-(24)yields:

Fig.3 Position transition of ICE from approaching to docking.

where x=x-x0,x=[V，α，β，p，q，r，ψ，θ，φ，xU，yU，zU]T,Vis the airspeed,α the angle of attack,β the angle of sideslip,xU，yU，zUare the positions;x0is the value of the trimmed states.u=u-u0,u=[δp，δe，δc，T],u0is the value of the trimmed inputs,δp，δe，δcare the angles of the surface.A0，B0are the state matrix and control matrix.

To ensure zero tracking error at the steady state condition,three integrals of the position error as additional states are augmented into the state vector as

The augmented state-space equation becomes

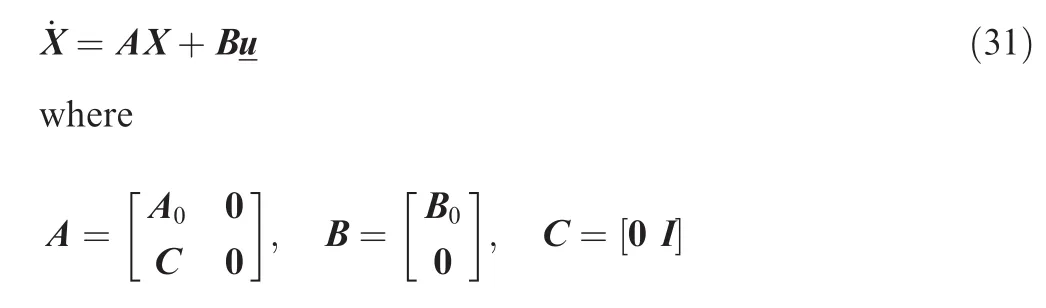
Using LQR design technique,the state feedback gain matrix K is obtained to minimize the cost function:

where Q is symmetric positive semi-definite and R symmetric positive definite.

Selecting Q,R and solving the Riccatiequations PA+ATP-PBR-1BTP+Q=0 yields the input

where K=R-1BTP,P is the symmetric positive semi-definite matrix.

3.Simulation results

3.1.Model of hose–drogue assembly with a nonlinear controller

The HDA is modeled by a sequence of variable-length links connected with frictionless joints as illustrated in Fig.412–16,where all variables can be found in Refs.12–16A set of iterative equations of the hose’s three-dimensional motion is derived subject to hose reeling in/out,tanker motion,hose restoring force due to bending,gravity,and aerodynamic loads accounting for the effects of steady wind,atmospheric turbulence,tanker vortex.Two nonlinear control strategies are designed to suppress the hose whipping phenomenon.For details of the model and its controller,see the research previously conducted by the authors.12–16

3.2.Modeling wind effects

The aerodynamic forces and moments on a receiver aircraft are created by its motion relative to the surrounding air.5The air itself is in motion relative to the inertial frame to form the wind.The wind effects acting on the receiver aircraft should consist of two parts,the uniform local winds and the nonuniform wind induced by the wake vortex of the tanker.

The effects of the uniform local winds,including the gust,the turbulence,the horizontal wind,and the wind shear,could be directly applied to the center of mass of the receiver aircraft.To highlight the mass change effects on the receiver’s states,verylightDryden wind turbulence(wind speed range:0–0.03 m/s)is carried out in simulation,because attitudes(φ，θ，ψ),angle of attack and side-slip angle(α，β)of the receiver in the close range aerial refueling scenario are little and serious Dryden wind turbulence will cover up them.

However,the vortex-induced wind field acting on the receiver aircraft is nonuniform in nature,which could not be directly applied to the center of mass of the receiver aircraft.For simplicity,with a 39.88 m wing span and a 2.85 m distance between the pod and the top of the right wing,the vortex model and averaging technique derived by Dogan et al.17–19are employed to approximate the effects of the vortexinduced wind field on the center of mass of the receiver aircraft.A vertical slice of the wake 10 m behind the tanker is illustrated in Fig.5.The equivalent component of the wind vectorVwzacting on the receiver’s center of mass along the tanker’szaxis in the vortex-induced wind field is shown in Fig.6

Thus,the velocity Vrand angular velocity vector ωrof the center of mass of the receiver aircraft with respect to the surrounding air are given by

where Vwand ωware the velocity vector and angular velocity vector of the uniform local winds.Vvand ωvare the equivalent velocity vector and equivalent angular velocity vector induced by the tanker vortex.

Then,to be able to use the equations of motion of the receiver aircraft without modification,Vrand ωr,rather than Vband ωb,could be used in the calculation of aerodynamic forces and moments.

Fig.4 Configuration and modeling assumptions of a hose–drogue aerial refueling system.12–16

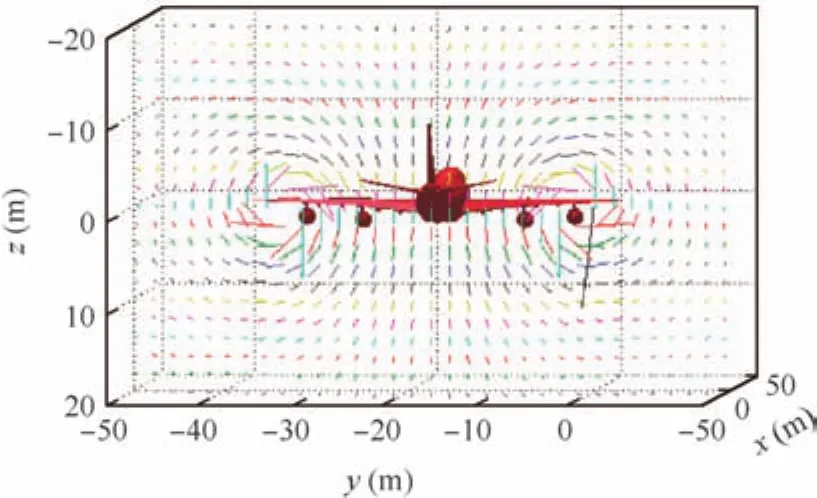
Fig.5 Vertical slice of tanker wake 10 m behind tanker.

3.3.Simulation of autonomous aerial refueling

To validate the integrated simulation environment for probedrogue-based autonomous aerial refueling,the nonlinear equations of motion of the ICE relative toOnxnynznare implemented in simulation along with KC-135R.Both the receiver and the tanker models are equipped with their own controller based on LQR.The nominal altitude of the tanker is 7010 m with a speed of 200 m/s in a steady level flight.Other parameters used in simulation are set as follows.

(1)The center of mass positions of the forward tanks and the aft tanks are(4,±4,0.2)and(-4,±4,0.2)respectively relative to the receiver aircraft body frame.a1x=a2x=b1y=b2y=b3y=b4y=2 m, and a3x=a4x=4 m.The initial quantity of the fuel in each tank is set to be 10%of the total capacity,i.e.,214.8 kg in Tank 1 and Tank 2,389.8 kg in Tank 3 and Tank 4.For simplicity,it is assumed that the engine pumps the identicalfuelflow distribution from each tank.am=0.12 kg/s2.Other parameters about ICE can be found in Ref.11

(2)LOR controller gains: Q=10-2× diag{1，1，1，1，1，1，1，1，1，2，0.01，2，2，0.01，2},R=10-3×diag{0.00001，1，1，1}.

(3)Relative to the tanker’s body frame,FP,TP,and PP are set equal to(-31,34,2),(-52.8,34,12),and(-52.8,18.2,12).DP is a variable depending on the position of the drogue,which is decided by the HDA model in previous research conducted by the authors.12-16

Fig.6 Equivalent component of wind vector along tanker’s z axis in the vortex-induced wind field.

3.3.1.Approaching and docking phase

The ICE is initially at(-31,34,2)m inObxbybzbof the tanker and should approach and dock with a drogue for refueling along the reference trajectory programmed above.Figs.7–13 depict the results of the simulations when executed for an approaching and docking flight before refueling.

Fig.7 shows the actual trajectory and the reference trajectory of the ICE relative toObxbybzbof the tanker during approaching and docking.Fig.8 illustrates the triaxial details and the tracking errors of the trajectory.As seen from Figs.7 and 8,under the influences of the fuel consumption and the aerodynamic disturbance,the LQR controller still enables the ICE to track the reference trajectory exactly.

Figs.9 and 10 show the time histories of the mass of the fuel and the inertia of the ICE due to fuel consumption by the engine during approaching and docking.

As seen from Fig.9 and Fig.10,the mass of the fuel and the inertia of the ICE decrease due to fuel consumption by the engine throughout the approaching and docking flight.As a result of the fuel tank symmetry,Ixy,Iyx,Iyz,andIzyalways maintain to be 0.From Eq.(28),the rate of the fuel consumption by the engine depends on the thrust.Therefore,the rate of the fuel consumption increases gradually in pace with the transition from the deceleration to the acceleration of the receiver as shown in Fig.11.

The true airspeed,the aerodynamic angles,and the orientation of the ICE are presented in Figs.11 and 12.Fig.13 illustrates the values of the elevon δe,pitch flap δp,and clamshell δcdeflections and the thrust.

As shown in Figs.5–7,outside the wing of the tanker,the local airflow of the vortex flows upward.If the controller does not respond,the angle of attack α will increase,thexcomponent of the true airspeedVwill decrease,and then the receiver will not be able to track the reference trajectory exactly.Therefore,from the FP to the TP,about 0–150 s,the controller negatively increases δpto decrease the pitch angle θ of the ICE to resist continuous growth of α.Thexcomponent of the gravity of the ICE due to the decreased pitch angle,except for the effect of the deceleration of the ICE,will decrease the thrust.As a result,the fuel consumption will be decreased with respect to a level flight.However,the condition inside the wing of the tanker,about 150–300 s,is exactly opposite of a bond.Due to the fuel tank symmetry,lateral states and control variables in the steady state tend to 0 in the presence of the disturbance caused by the vortex and the Dryden wind turbulence.

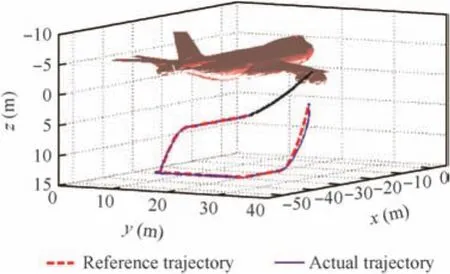
Fig.7 Actual trajectory and reference trajectory of ICE relative to tanker.

Fig.8 Triaxial details and tracking errors of trajectory.

Fig.9 Time histories of fuel mass considering fuel consumption by engine.

Fig.10 Time histories of inertia of ICE considering fuel consumption by engine.

Fig.11 Time histories of true airspeed and aerodynamic angles.

Fig.12 Time histories of orientation.

3.3.2.Station-keeping and refueling phase

After docking,the ICE should maintain a steady position relative toObxbybzbof the tanker to receive 0.04416 m3/s of JP-4 fuel.Figs.14–19 depict the results of the simulations during the station-keeping and refueling phase for three different cases as the same as three cases used in Ref.11Case 1:both forward tanks refuel first,but at half of the maximum flow rate,until each is half full.Next,both aft tanks refuel,again at half of the maximum flow rate,until each is half full.Case 2:neither of the right-hand fuel tanks receives fuel,but the lefthand forward tank is fully fueled first,followed by the lefthand aft.Case 3:the right-hand forward and left-hand aft tanks do not fill,but the other tanks fully fuel,with the forward tank refueling first.To allow for better comparisons,the fuel tanks in Case 1 only fill to half capacity so that the transition from refueling the forward tanks to the aft tanks occurs at the same time in all three cases.In addition,the postrefuel total aircraft weight is identical for three cases.In each case,refueling starts att=300 s.

Figs.14 and 15 illustrate the ICE’s position with respect to the docking position.The controller,as expected,has the same station-keeping performance for three cases except spikes inxandzposition deviations when fuel flow starts.The variations of longitudinal states of the ICE,i.e.,thexandzdeviations from the docking position,V,α,θ,δp,andTas seen later,have the same tendencies.

Figs.9 and 10 show the time histories of the mass of the fuel and the inertia of the ICE due to the fuel transfer as well as the fuel consumption by engines during station-keeping and refueling.Each fuel tank is filled with the fuel as stated above for three cases.To the end of refueling at about 467 s,the total fuel filled in the ICE(eliminating the fuel consumed by engines)is 5670.5 kg accounting for 46.06%of the initial weight of the ICE.

As shown in Figs.16 and 17,Ix,Iy,Iz,Ixz,andIzxhave identical tendencies for all three cases due to thexOzplane of symmetry of the ICE.Under this condition,for every productyjzjoryjxjin an inertia computation there is a different value for a different case.Therefore,Ixy,Iyx,Iyz,andIzyare different for three cases.

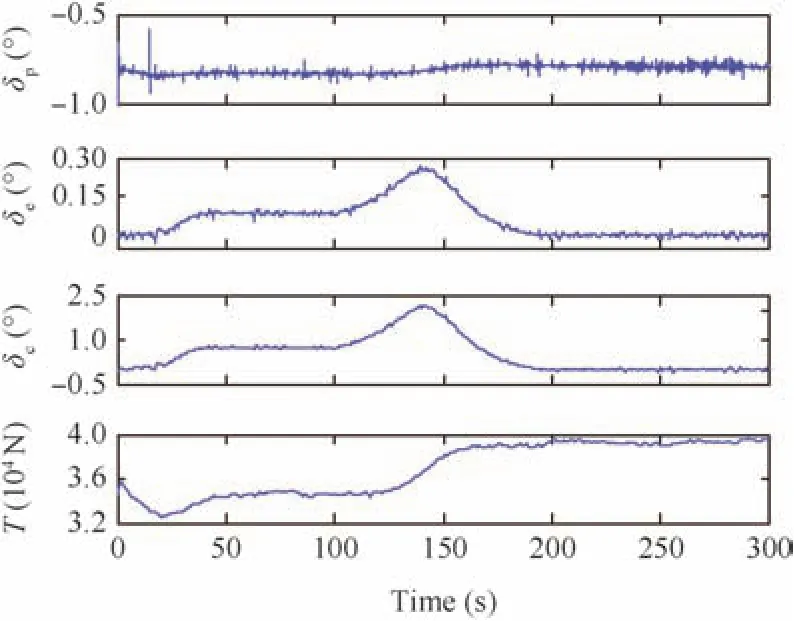
Fig.13 Time histories of actuators and thrust.

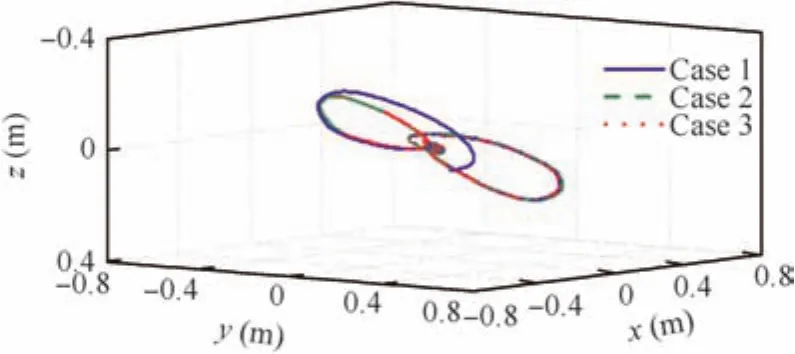
Fig.14 ICE’s position variations with respect to docking position.

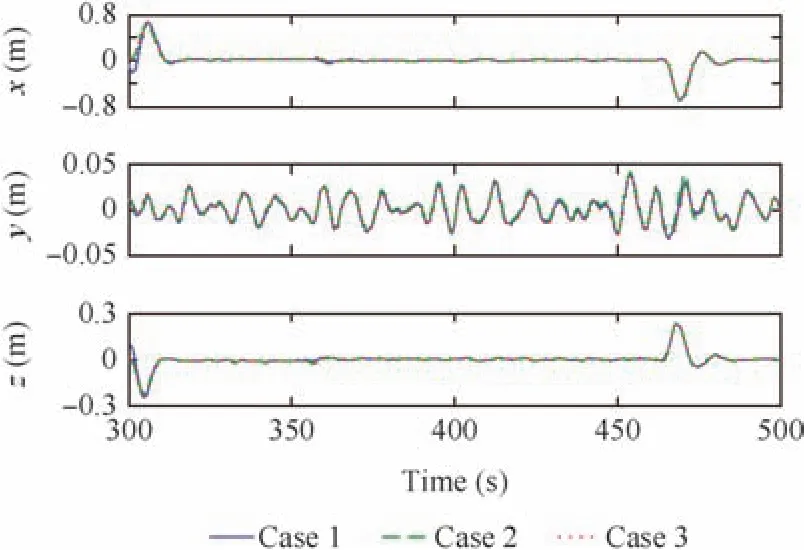
Fig.15 Triaxial details of ICE’s position variations with respect to docking position.

Fig.16 Time histories of fuel mass during fuel transfer.

Fig.17 Time histories of inertia of the ICE during fuel transfer.

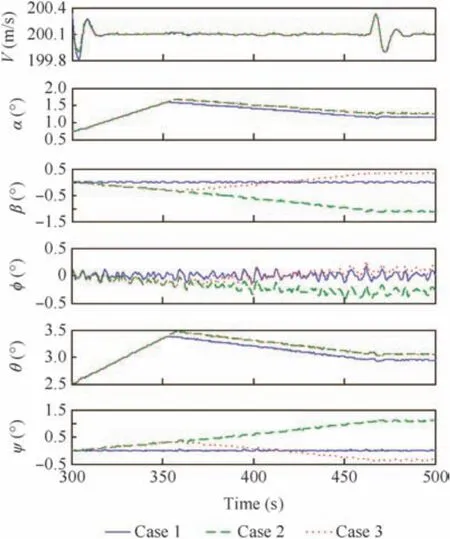
Fig.18 Time histories of orientation of the ICE during fuel transfer.

Fig.19 Time histories of actuators and thrust of ICE during fuel transfer.

Fig.18 illustrates the deviations of the airspeed and the orientation respectively.The controller,as expected,has the same speed-keeping performance for three cases except spikes when fuel flow starts.As stated above,the variations of longitudinal states of the ICE for three cases have the same tendencies.Before aft tanks are filled with the fuel for three cases,α and θ are increased by the controller to increase the upward moment to compensate for the effects of the forward tank.At this time,the deviations of the lateral states are still small.Therefore,α and θ have identical trajectories for all three cases.After the aft tanks are filled with the fuel for three cases,the gravity of the aft tanks grows gradually and lowers the values of the longitudinal states than before.For Cases 2 and 3,the effects caused by the fuel transfer could be regarded as identical for the longitudinal states of the ICE based on thexOzplane of symmetry.However,the asymmetric refueling in Cases 2 and 3 produces an asymmetric moment in the lateral direction due to the fuel tank gravity.To keep lateral balance and track the commanded speed,the controller makes the ICE roll or yaw a small angle in the corresponding direction to compensate for the opposite-side tank refueling.As a result,the component of the lift in the gravitational direction decreases and must be compensated by larger longitudinal states than Case 1.When compared to the same side forward to aft tank transition of Case 2,the opposite-direction tendencies of the sideslip,roll,and yaw angles immediately follow the Case 3 transition from the forward to the diagonal aft fuel tank to compensate for the opposite-side tank refueling and maintain a commanded steady level flight.After completion of the refueling,the longitudinal trim states are a little larger than their initial values to produce enough lift.The roll and yaw angles are the smallest for Case 1,which results in zero deviations as expected based on the symmetry,while the roll and yaw trim angles are different for Cases 2 and 3.This demonstrates the effect of the asymmetric mass distribution on the steady-state trim condition.

Fig.19 illustrates the values of δe,δp,δcdeflections and the thrust for three cases.A comparison can be made between Figs.18 and 19 to show how the effectors react to the refueling in three cases and how their steady-state positions correspond to the receiver’s steady-state Euler angles.The longitudinal control variables,i.e.,δpand the thrust,match the longitudinal states shown in Fig.18.When the refueling of Case 3 transitions from the forward to the diagonal aft tank,both δeand δcreact immediately to compensate for the opposite-side tank refueling.The magnitude of the effecter deflections changes steadily throughout the refueling to account for the steadily growing fuel tank masses.This is caused by the contribution of the gravitational moment caused by the fuel masses to the total moment of the external forces about the origin ofObxbybzbof the ICE.The thrusts in Fig.19 for three cases,which prove to be very similar,tend to grow as the refueling occurs to keep the receiver at the commanded velocity while experiencing mass increase.The steady-state thrust value is somewhat higher than initially due to the higher postrefuel aircraft weight.

For ease of comparison,two of the simulation results in Ref.11are cited as Figs.20 and 21.It is known to all that if the fuel mass in one tank is refueled gradually,the states of the receiver should also change gradually with it.The tendency of the state variation should not change unless the refueling course changes.But known from Figs.20 and 21,there exists an obvious state mutation(especially the yaw and the clamshell),when each thank is filled,which goes against the continuity of the physical system as stated above.Taking the clamshell in the Case 3 as an example,the deflection should monotonically increase to the maximum in a direction.Then the deflection should go through the same process but in the other direction,when the transition from refueling the forward tanks to the aft tanks occurs,because the fuel is always filled at a constant flow rate.Besides,the deflection should always maintain a maximum in the relevant direction after the refueling stops.Therefore,although the model in Ref.11have a correct mathematical derivation,some mistakes occur in the simulation application.Fortunately,this phenomenon does not appear at all in the model proposed here.

Fig.20 Time history of receiver relative orientation deviation in straight level flight.

Fig.21 Time history of receiver control surface deflections in straight level flight.

4.Conclusions

(1)Taking into account three major factors,i.e.,the dynamic models of the receiver with the time-varying inertia property,an HDA dynamic model with the variable-length property,and the wind effect due to the tanker’s trailing vortices,an integrated simulation environment for probe-drogue-based autonomous aerial refueling is developed.The environment could be used to further develop and evaluate aircraft control,sensor systems,dynamics and modeling in the autonomous aerial refueling research.

(2)Considering a rectangular shape of the tanks rather than a lumped mass,a set of new simpler equations of motion of an aircraft with the time-varying inertia property due to fuel transfer as well as the fuel consumption by engines is derived relative to the ECI frame or the NED frame.

(3)The ICE as the receiver and a LQR-based autonomous flight controller is employed to validate the integrated simulation environment for probe-drogue-based autonomous aerial refueling.

Acknowledgments

This research was supported by the National Natural Science Foundation of China(Nos.61473307,61304120).

1.Thomas PR,Bhandari U,Bullock S,Richardson TS.Advances in air to air refueling.Prog Aerosp Sci2014;71:14–35.

2.Quan Q,Wei ZB,Gao J,Zhang RF,Cai KY.A survey on modeling and control problems for probe&drogue autonomous aerial docking.Acta Aeronaut Astronaut Sin2014;35(9):2390–410[Chinese].

3.Lu YP,Yang CX,Liu YY.A survey of modeling and control technologies for aerial refueling system.Acta Aeronaut Astronaut Sin2014;35(9):2375–89[Chinese].

4.Dong XM,Xu YJ,Chen B.Progress and challenges in automatic aerial refueling.J Air Force Eng Univ(Nat Sci Ed)2008;9(6):1–5[Chinese].

5.Lewis BL,Stevens FL.Aircraft control and simulation.New York:Wiley;1992.p.21.

6.Roskam J.Airplane flight dynamics and automatic flight controls.Lawrence:DAR Corporation;2001.p.5.

7.Bennington MA,Visser KD.Aerial refueling implications for commercial aviation.J Aircraft2005;42(2):366–75.

8.Bloy A,Khan M.Modeling of the receiver aircraft in air-to-air refueling.J Aircraft2001;38(2):393–6.

9.Venkataramanan S,Dogan A.Dynamic effects of trailing vortex with turbulence&time-varying inertia in aerial refueling.AIAA atmospheric flight mechanics conference.Reston:AIAA;2004.

10.Tucker J,Dogan A.Derivation of the dynamics equations of receiver aircraft in aerial refueling.45th AIAA aerospace sciences meeting.Reston:AIAA;2007.

11.Waishek J,Dogan A,Blake W.Derivation of the dynamics equations of receiver aircraft in aerial refueling.J Guid Control Dyn2009;32(2):585–97.

12.Wang HT,Dong XM,Dou HF,Xue JP.Dynamic modeling and characteristics analysis of hose-paradrogue aerial refueling systems.J Beijing Univ Aeronaut Astronaut2014;40(1):92–8[Chinese].

13.Wang HT,Dong XM,Xue JP,Liu JL.Dynamic modeling of hose–drogue aerial refueling system and integral sliding mode backstepping control for whipping phenomenon.Chin J Aeronaut2014;27(4):930–46.

14.Wang HT,Dong XM,Liu JL,Wang J.Dynamics and control of the hose whipping phenomenon in aerial refueling.2015 IEEE aerospace conference.Piscataway,NJ:IEEE Press;2015.

15.Wang HT,Dong XM,Guo J,Liu JL,Wang J.Modeling and analysis of the hose whipping phenomenon of the refueling hose–drogue assembly.Acta Aeronaut Astronaut Sin2015;36(9):3116–27[Chinese].

16.Wang HT,Dong XM,Guo J,Liu JL,Wang J.Modeling and simulation for autonomous aerial refueling using a probe-drogue system.AIAAatmosphericflightmechanicsconference.Reston:AIAA;2015.

17.Dogan A,Kim E,Blake W.Control and simulation of relative motion for aerial refueling in racetrack maneuvers.J Guid Control Dyn2007;35(5):1551–7.

18.Dogan A,Venkataramanan S.Nonlinear control for reconfiguration of unmanned-aerial-vehicle formation.J Guid Control Dyn2005;28(4):667–78.

19.Dogan A,Venkataramanan S,Blake W.Modeling of aerodynamic coupling between aircraft in close proximity.J Aircraft2005;42(4):941–55.

20.Tandale MD,Bowers R,Valasek J.Trajectory tracking controller for vision-based probe and drogue autonomous aerial refueling.J Guid Control Dyn2006;29(4):846–57.

21 January 2015;revised 19 May 2015;accepted 11 August 2015

Available online 5 March 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 29 84787400 801.

E-mail addresses: wanghaitao198638@163.com (H. Wang),dongxinmin@139.com(X.Dong).

Peer review under responsibility of Editorial Committee of CJA.

Wang Haitaoreceived his B.S.and M.S.degrees from Air Force Engineering University in 2009 and 2011,respectively.He is now pursing his Ph.D.degree there.His main research interests include system modeling,control and simulation of aerial refueling.

Dong Xinminis a professor at Air Force Engineering University.He received his B.S.and M.S.degrees from Northwestern Polytechnical University in 1983 and 1988,respectively,and then received his Ph.D.degree from Xi’an Jiaotong University in 1991.He has worked in the field of flight control for more 20 years,and his current research interests include modern control theory,machine vision,and autonomous aerial refueling.

Xue Jianpingis an associate professor at Air Force Engineering University.He received his B.S.and M.S.degrees from Air Force Engineering University in 1992 and 2005,respectively.His current research interests include computer control and system simulation.

Liu Jiaolongreceived his B.S.and M.S.degrees from Air Force Engineering University in 2011 and 2013,respectively.He is now pursing his Ph.D.degree there.His main research interests include CFD analysis and learning control.

Wang Jianreceived his B.S.degree from Air Force Engineering University in 2013.He is now pursing his M.S.degree there.His main research interests include CFD analysis,control and simulation of aerial refueling.