A novel two-stage extended Kalman filter algorithm for reaction flywheels fault estimation

Chen Xueqin,Sun Rui,Jing Wncheng,Ji Qingxin,Zhng Jinxiu

aResearch Center of Satellite Technology,Harbin Institute of Technology,Harbin 150080,ChinabSchool of Aeronautics and Astronautics,Shanghai Jiao Tong University,Shanghai 200240,China

A novel two-stage extended Kalman filter algorithm for reaction flywheels fault estimation

Chen Xueqina,*,Sun Ruia,Jiang Wanchenga,Jia Qingxianb,Zhang Jinxiua

aResearch Center of Satellite Technology,Harbin Institute of Technology,Harbin 150080,ChinabSchool of Aeronautics and Astronautics,Shanghai Jiao Tong University,Shanghai 200240,China

Fault estimation;Reaction flywheels;Satellite attitude control systems;Separate-bias principle;Two-stage extended Kalman filter

This paper investigates the problem of two-stage extended Kalman filter(TSEKF)-based fault estimation for reaction flywheels in satellite attitude control systems(ACSs).Firstly,based on the separate-bias principle,a satellite ACSs with actuator fault is transformed into an augmented nonlinear discrete stochastic model;then,a novel TSEKF is suggested such that it can simultaneously estimate satellite attitude information and actuator faults no matter they are additive or multiplicative;finally,the proposed approach is respectively applied to estimating bias faults and loss of effectiveness for reaction flywheels in satellite ACSs,and simulation results demonstrate the effectiveness of the proposed fault estimation approach.

1.Introduction

The separate-bias estimation algorithm is used to estimate the state and constant bias of linear systems.The basic principle of this algorithm,which is also called two-stage Kalman filter(TSKF),is to estimate system states and constant biases separately,then obtain the optimal estimate using the coupling relationship between them.In 1969,Friedland firstly proposed the separate-bias estimation algorithm1and made a further investigation.2,3During the past four decades,many research achievements have been reported on this algorithm.At present,the main research on this topic is concerned with estimation of constant/time-varying bias and all kinds of engineering applications.

Recently,many scholars have paid considerable attention to separate-bias estimation algorithm for linear systems.4–6Keller and Darouach4suggested an optimal solution of the TSKF,which can be used to estimate optimal state and optimal random bias,and further a two-stage optimal strategy was developed for discrete-time stochastic linear systems subject to intermittent unknown inputs.5Khabbazi and Esfanjani6proposed a constrained TSKF for tracking control problem in an uncertain linear system and its main advantage is the improvement of estimation accuracy.

For fault/bias estimation of nonlinear systems,much progress has been made on EKF-based approaches.EKF-based sub-optimal algorithm was proposed in Ref.7.Zhou et al.investigated a pseudo separate-bias estimation algorithm for nonlinear time-varying stochastic systems.8,9In Ref.10,fuzzyKalman filter-based approach was proposed for nonlinear stochastic discrete time systems.

Based on the general TSKF,Hsieh11proposed a general two-stage extended Kalman filter(GTSEKF)-based constant parameter estimation approach.In Ref.12,an adaptive TSEKF like Ref.11was proposed to estimate the closed-loop position and speed of sensorless control for permanent magnet synchronous motor.Kim13proposed an adaptive TSEKF for INS-GPS loosely coupled systems and its main advantage was it cost less computation time due to the introduction of the forgetting factor.In Ref.14,an adaptive TSEKF algorithm based on Ref.13was introduced to the application of geomagnetic aided inertial navigation filtering.By introducing strong tracking multiple fading factors and embedding EKF into an optimal TSKF,a novel robust filter-based bearings-only maneuvering target tracking problem was investigated,which can provide an optimal estimation of the target state and the unknown statistical parameters of virtual noises.15

The faults of actuators and sensors in control systems can be represented as biases via separate-bias estimation algorithm.Fault estimation for dynamic systems has attracted considerable attention during the past two decades.When estimating the additive actuator/sensor faults,the algorithm can be implemented easily since the biases representing faults in these models have specific physical meanings and the principles are clear.16When estimating the multiplicative faults in actuators,it is necessary to use other parameters to represent the fault models,such as control effectiveness factors,which can be used to indicate the fault degree of control systems.By introducing forgetting factors into the optimal TSKF in Ref.4,an adaptive TSKF was exploited to estimate the abrupt reduction of control effectiveness in dynamic systems by Wu et al.17This algorithm is applied for the identification of impairment in its control surfaces in an aircraft model.In Refs.18–22,a further investigation on this algorithm was made and widely applied it on fault diagnosis and fault-tolerant control.In Ref.23,control effectiveness factor estimation was extended to the estimation of control distribution matrix elements,and the TSKF was applied to actuator/surface fault diagnosis and fault-tolerant control of F-16.In recent years,this method has been applied to the fault diagnosis and fault-tolerant control of sensors and actuators in satellite attitude control system.16,24–26The value of the effectiveness factors can be derived via this method and system fault degree can be analyzed to obtain biases for the fault-tolerant control purpose.In addition,to the best of our knowledge,separatebias principle never considers additive faults and multiplicative faults simultaneously.

In view of this,this paper investigates TSEKF-based fault estimation for reaction flywheels in satellites.A novel TSEKF is suggested such that it can simultaneously estimate satellite attitude information and reaction flywheel faults no matter they are additive or multiplicative.It is respectively applied to estimating bias faults and loss of effectiveness for reaction flywheels in a satellite ACSs,and the simulation results demonstrate the effectiveness of the proposed fault estimation approach.

2.System fault model

Consider the following nonlinear discrete-time stochastic system with bias vector of unknown magnitude bk∈Rp:

where xk∈Rnis the system state;yk∈Rmis the measurement vector;the noise sequence wbk,wxkand vkare zero-mean uncorrelated Gaussian random sequences with

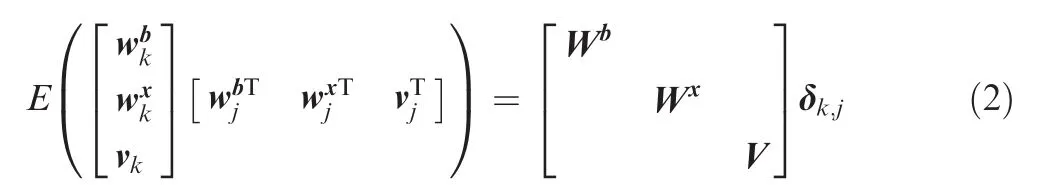
where Ak∈Rn×nand Ck∈Rm×nare state transition matrix and observation matrix,respectively,and we have

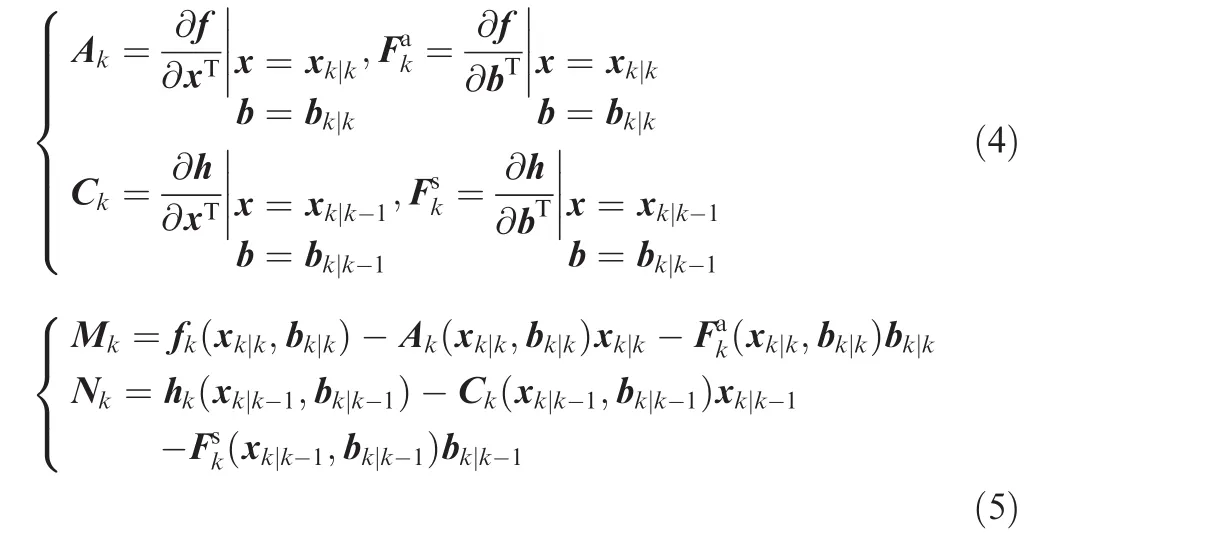
where xk|kand bk|kdenote the optimal results of xkand bkrespectively.

The vector function ω =[ωx， ωy， ωz]Trepresents the inertially referenced satellite angular rate vector of the satellite body relative to the inertial coordinate system and the corresponding Euler angles are φ, θ and ψ. Define x=[ωx， ωy， ωz， φ， θ， ψ]T,the state equation of satellite attitude control system based on the satellite attitude dynamics equation can be given as

u（x）∈ Rlis the known control input vector;B ∈ Rn×lis the control input matrix;Isis the moment of inertial matrix of the satellite.

Observation equation is

where C=I6is the output matrix,and Inis ann×nidentity matrix.

Discretize the combination of Eqs.(6)and(8),then the system model without fault is established like Eq.(1).

(1)Additive fault model

The bias bkrepresents additive faults of actuators,and the system model with additive faults of actuators can be described as

where gk,Bk,ukand Ckare the corresponding discrete system matrices of Eqs.(6)and(8),the corresponding matrix of Eq.(1)is

(2)Multiplicative fault model

Here,bkrepresents the degree of the multiplicative faults of actuators,and the bias Λkukrepresents the multiplicative faults of actuators,in which diagonal matrix Λk=diag（bk）.The system model with multiplicative faults of actuators can be described as

the corresponding matrix of Eq.(1)is

In Eq.(11),the vector function bkis also called the control effectiveness factors,representing the possible loss of control effectiveness in the model,21–23whose value is 0 in the absence of multiplicative faults.

The objective of this paper is to design a TSEKF such that it can estimate actuator faults no matter they are additive or multiplicative.That is,it can give a solution for system Eq.(1)with the unknown bias and system states,a solution for additive fault system Eq.(9)with additive faults and system states,and also a solution for multiplicative fault system Eq.(11)with multiplicative faults and system states.

3.TSEKF-based actuator fault estimation approach

In this section,a novel TSEKF is designed to simultaneously estimate satellite attitude information and actuator faults.

Theorem 1.A discrete-time TSEKF is given by the following coupled difference equations when the nonlinear discrete-time stochastic system with bias vector of unknown magnitude is given by Eq.(1).

The unknown bias-free filter is

The unknown bias filter is

with the coupling equations

To facilitate the derivations,the following notations are used:

then the model Eq.(1)could be written as

A common approach to estimate the system state of system Eq.(31)is using the following well-known KF:

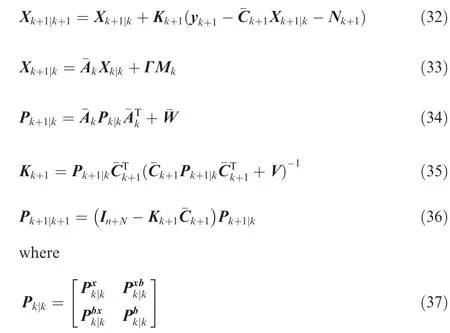
The one-step prediction value Xk+1|kis then transformed to promote the one-step prediction variance into a diagonal matrix.The orthogonal transformation matrix is chosen as

Define new variables

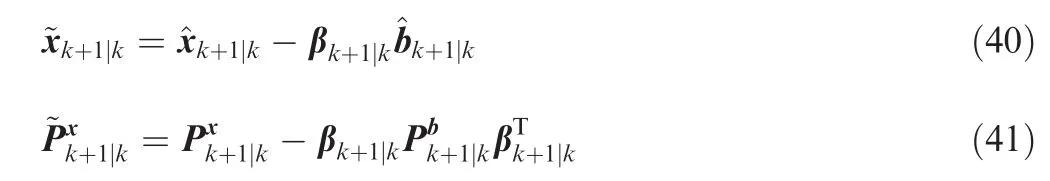
Then from Eqs.(38)and(41),we can get Eq.(29).Eq.(21)can be derived from Eq.(34)directly.From Eqs.(34)–(36)and Eq.(4),we have

According to the rule of finding the inverse of partitioned matrix and Eq.(37),we can get

Then it can be changed to Eq.(14),and in Eq.(45),we have

From Eqs.(44)and(46),we can get Eq.(17).Eq.(27)can be derived from Eq.(47)directly.

From Eqs.(43)and(45),Eq.(35)can be changed to

Then Eq.(26)can be obtained from Eq.(51).

Defining

Substituting Eq.(51)into Eq.(50),we have

Then Eq.(22)is obtained from Eqs.(54)and(23).Eq.(15)can be derived from Eq.(32)directly.From Eqs.(15)and(47),Eq.(55)can be simplified into Eq.(13).

From Eq.(48),we have

Eq.(25)can be derived from Eq.(29)directly.Eq.(24)is obtained by substituting Eq.(56)into Eq.(51).Eq.(42)is obtained by substituting Eq.(4)into Eq.(18).

Remarks.

(1)The TSEKF,which is given by Eqs.(13)–(29),is equivalent to the TSKF whenMk=0andNk=0in Eq.(5).

(2)System states and bias of Eq.(1)can be estimated based on Theorem 1.

(3)System states and additive faults of Eq.(9)can be estimated based on Theorem 1.

(4)System states and multiplicative faults of Eq.(11)can be estimated based on Theorem 1.

(5)The basic idea of this theorem is TSKF,so the TSEKF has the same advantages of low computational cost and high estimation precision as TSKF.

(6)The TSEKF processes the nonlinear terms in system model Eq.(1)with the same way of EKF.This way can motivate the generalization of the linear TSKF to nonlinear systems.

4.Fault simulation on closed-loop satellite attitude control systems

Actuators in closed-loop ACSs are three reaction flywheels.Sensors in closed-loop ACSs are three gyros and two star sensors.Without loss of generality,we assume that the fault happens in the reaction flywheel alongxaxis.

Here,we consider two simulation backgrounds:attitude stabilization control and attitude tracking control.The former is considered for additive faults estimation.The latter is mainly considered for multiplicative fault estimation.To estimate multiplicative fault for reaction flywheels,satellite ACSs must satisfy the persistent excitation condition.In other words,reaction flywheels should be activated to ensure satellite attitude maneuver or tracking.

4.1.Faults conditions and simulation parameters

The conditions of the additive faults and the multiplicative faults are given as follows.

Condition 1.The first fault b1=[0.005， 0， 0]TN ·m exists during the time interval 200 s≤t1＜400 s,and the second fault b2=[0.010， 0， 0]TN·m exists during the time interval 400 s≤t2＜600 s.

Condition 2.The control effectiveness factors of the first fault b1=[0.3， 0， 0]Texist during the time interval 200≤t1＜400 s,and the control effectiveness factors of the second fault b2=[0.5， 0， 0]Texist during the time interval 400≤t2＜600 s.

The conditions of the simulation and initial values are chosen as follows.

(1)Themaximum outputtorqueoftheflywheelsis 0.15 N·m and the maximum angular momentum is 15 N ·m ·s.

(2)The moment of inertial of the satellite is Is=diag（200，100，300）kg˙s m2.

(3)The PD controller is chosen with its gains:u=-[KP， KD]（x-xd）,with KD=[36 18 54]Tand KP=[2 1 3]T.

(4)For attitude stabilization control,xd=06×1.

(6)The initial state is x0=06×1.

(7)The initial transfer matrix is P0=I6.

(8)The process noise covariance matrix is W=diag（σ2ωI3，σ2ΦI3）,where σω=2 × 10-4rad/s, σΦ=5×10-5rad.

(9)The measurement noise covariance matrix is V=0.0012I6.

(10)The sampling periodkis 0.01 s.

4.2.Simulation results

(1)Fault estimation under attitude stabilization control.

The TSEKF algorithm proposed in this paper is applied for fault estimation of attitude stabilization under Condition 1.The simulation results are shown in Fig.1.

For attitude stabilization control,the fault estimation results using TSEKF algorithm and TSKF algorithm are the same:0.005 N ·m and 0.010 N ·m.

The estimation results of multiplicative faults cannot be obtained under the same attitude stabilization control background under Condition 2.That is,the precondition of estimating the multiplicative faults of actuators is that the control torque output of actuators must not be approximately equal to zeroes.So,we have to estimate the multiplicative faults of actuators under attitude tracking control with a persistent excitation.

(2)Fault estimation under attitude tracking control.

The system model of attitude tracking control is nonlinear,which makes the normal TSKF useless.The TSEKF algorithm proposed in this paper is applied to fault estimation of attitude maneuver under Condition 1 and Condition 2.The simulation results are shown in Figs.2 and 3.

For attitude tracking control,the fault estimation results usingTSEKFalgorithmare0.005 N ·mand0.010 N ·m.When the fault occurs,the trough and peak of the attitude angle curve are-58.942°and 59.372°respectively,while the trough and peakoftheattitudeanglecurveare-59.085°and59.085°respectivelywithoutfaults.Thatis,after thefirstfaultoccurs,abiasof-0.143°isaddedtotheattitudeangle,andafterthesecondfault occurs,a bias of-0.287°is added to the attitude angle.

For attitude tracking control,the estimation results of control effectiveness factors using TSEKF are 0.3 and 0.5 respectively,and the MSE is 7.8×10-4.

According to the simulation results,there is no obvious difference between the TSEKF and the TSKF in fault estimation of linear system(such as attitude stabilization control).While in fault estimation of nonlinear system(such as attitude tracking control),in which the TSKF cannot be applied,we can get good performances on the basis of TSEKF.

Fig.1 Simulation results of attitude stabilization under Condition 1.

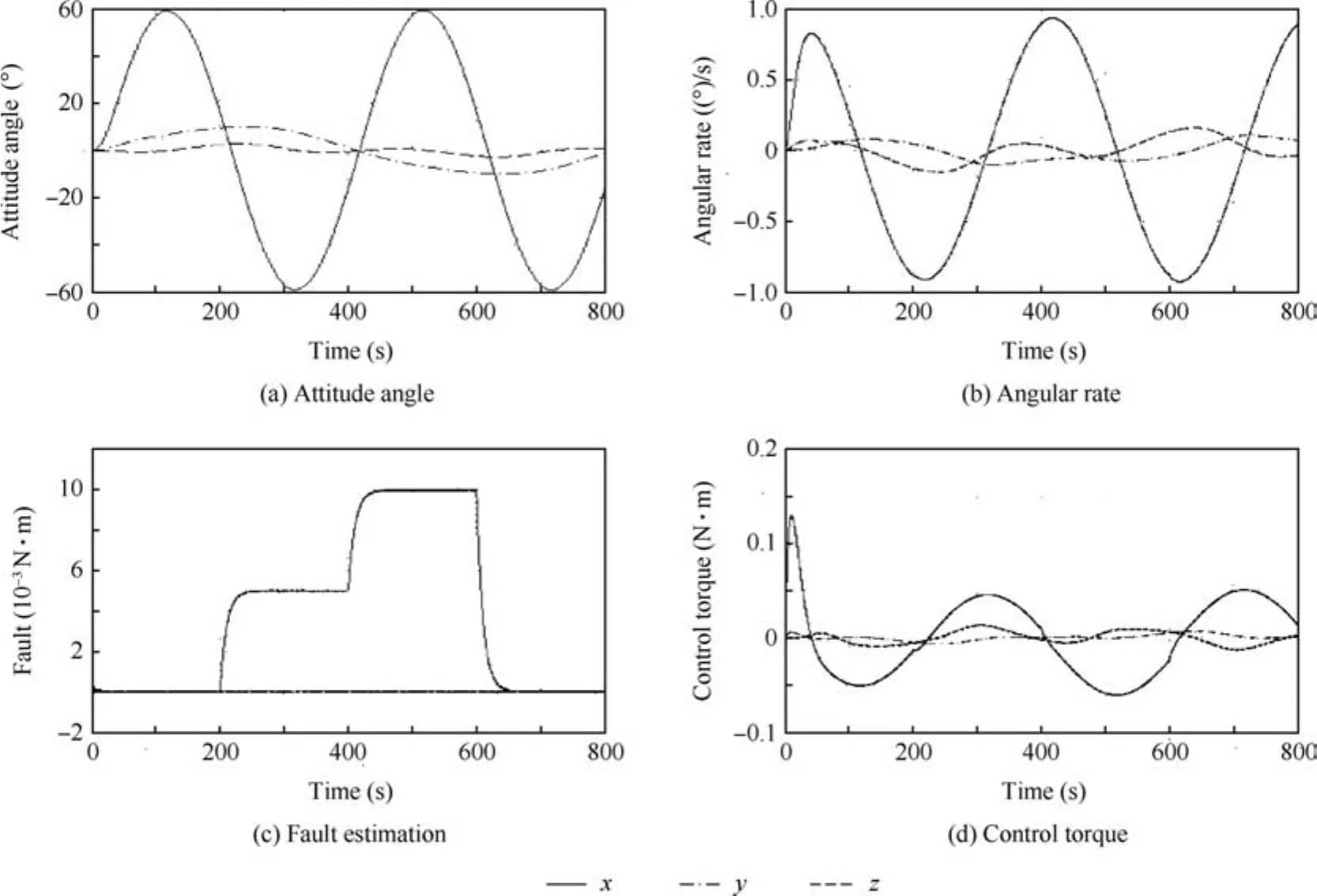
Fig.2 Simulation results of attitude tracking control under Condition 1.

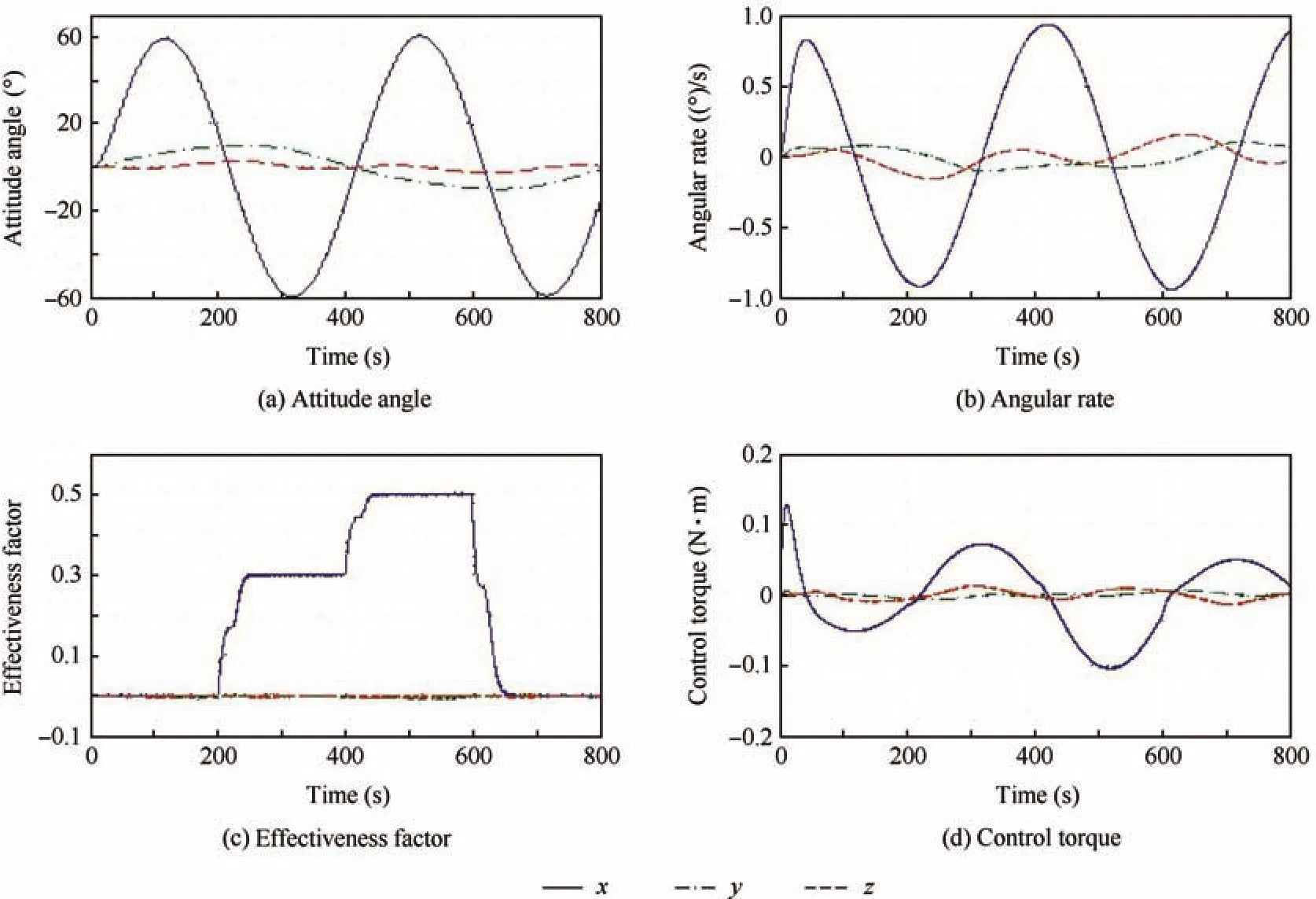
Fig.3 Simulation results of attitude tracking control under Condition 2.

5.Conclusions

This paper has investigated the problem of two-stage extended Kalman filter-based reaction flywheel fault estimation.

(1)Based on the separate-bias principle,motivated by the optimal TSKF and EKF,employed EKF to process nonlinear terms in nonlinear system model,a novel TSEKF algorithm is designed such that it cannot only estimate satellite attitude angular rates and Euler angles,but also estimate reaction flywheel faults no matter they are bias ones or loss of effectiveness.

(2)It is respectively applied to estimating bias faults and loss of effectiveness for reaction flywheels in a satellite ACSs.Simulation results validate the feasibility and effectiveness in the cases of both attitude stabilization and attitude tracking control.

1.Friedland B.Treatment of bias in recursive filtering.IEEE Trans Autom Control1969;14(4):359–67.

2.Friedland B.Recursive filtering in the presence of biases with irreducible uncertainty.IEEE Trans Autom Control1976;21(5):789–90.

3.Friedland B.Notes on separate-bias estimation.IEEE Trans Autom Control1978;23(4):735–8.

4.Keller JY,Darouach M.Optimal two-stage Kalman filter in the presence random bias.Automatica1997;33(9):1745–8.

5.Keller JY,Sauter D.Kalman filter for discrete-time stochastic linear systems subject to intermittent unknown inputs.IEEE Trans Autom Control2013;58(7):1882–7.

6.Khabbazi MR,Esfanjani RM.Constrained two-stage Kalman if lter for target tracking.In:Proceedings of the 4th international conference on computer and knowledge engineering(ICCKE);2014 Oct 29–30;Mashhad.Piscataway(NJ):IEEE Press;2014.p.393–7.

7.Caglayan AK.A separated bias identification and state estimation algorithm for nonlinear systems.Automatica1983;19(5):561–70.

8.Zhou DH,Sun YX,Xi YG,Zhang ZJ.A pseudo separate-bias estimation algorithm for input and output bias of a class of nonlinear systems.Control Decis1992;7(3):217–20[Chinese].

9.Zhou DH,Sun YX,Zhang ZJ.Extension of Friedland’s separatebias estimation to randomly time-varying bias of nonlinear systems.IEEE Trans Autom Control1993;38(8):1270–3.

10.Talel B,Ben Hmida F.Fuzzy Kalman filter for nonlinear stochastic systems.In:Proceedings of 2013 10th international multi-conference on systems,signals&devices(SSD);2013 Mar 18– 21;Hammamet.Piscataway(NJ):IEEE Press;2013.p.1–7.

11.Hsieh CS.General two-stage extended Kalman filters.IEEE Trans Autom Control2003;48(2):289–93.

12.Yi B,Kang L,Tao S,Zhao X,Jing Z.Adaptive two-stage extended Kalman filter theory in application of sensorless control for permanent magnet synchronous motor.Math Prob Eng2013;2013,974974-1-13.

13.Kim KH,Lee JG,Chan GP.Adaptive two-stage extended Kalman filter for a fault-tolerant INS-GPS loosely coupled system.IEEE Trans Aerosp Electron Syst2009;45(1):125–37.

14.Liu M,Wang HJ,Guo QY,Feng JX.Application of the adaptive two-stage EKF algorithm in geomagnetic aided inertial navigation.In:Proceedings of the 2nd international conference on intelligent control and information processing(ICICIP);2011 Jul 25– 28;Harbin.Piscataway(NJ):IEEE Press;2011.p.697–701.

15.Yang J,Ji H.A novel robust two-stage extended Kalman filter for bearings-only maneuvering target tracking.Int J Phys Sci2011;6(5):987–91.

16.Li DB,Chen XQ,Li CL.Fault diagnosis of satellite actuator based on bias-separated theory.Syst Eng Electron2015;37(3):606–12[Chinese].

17.Wu NE,Zhang YM,Zhou KM.Control effectiveness estimation using an adaptive Kalman estimator.In:Proceedings of the IEEE international symposium on computational intelligence in robotics and atutomation;1998 Sep 14–17;Gaithersburg(MD).Piscataway(NJ):IEEE Press;1998.p.181–6.

18.Wu NE,Zhang YM,Zhou KM.Detection,estimation,and accommodation of loss of control effectiveness.Int J Adapt Control Signal Processs2000;14(7):775–95.

19.Zhang YM,Zhang HC,Dai GZ.A new bias partitioned squareroot information filter and smoother for aircraft state and parameter estimation.In:Proceedings of the 31st IEEE conference on decision and control;1992 Dec 16–18;Tucson(AZ).Piscataway(NJ):IEEE Press;1992.p.741–2.

20.Yu X,Jiang J.Hybrid fault-tolerant flight control system design against partial actuator failures.IEEE Trans Control Syst Technol2012;20(4):871–86.

21.Zhang YM,Jiang J.Integrated design of reconfiguration faulttolerant control systems.J Guid Control Dyn2000;1(24):133–6.

22.Fan JF,Zhang YM,Zheng ZQ.Robust fault-tolerant control against time-varying actuator faults and saturation.IET Control Theory Appl2012;6(14):2198–208.

23.Hajiyev C.Two-stage Kalman filter-based actuator/surface fault identification and reconfigurable control applied to F-16 fighter dynamics.Int J Adapt Control Signal Process2013;27(9):755–70.

24.Chen XQ,Ma YH,Wang F,Geng Y.Research on improved integrated FDD/FTC with effectiveness factors.J Syst Eng Electron2012;23(5):768–74.

25.Chen XQ,Zhang YC,Geng YH,Li HY.Satellite attitude control system on-orbit reconfigurable fault-tolerant control based on the control effectiveness factor.J Astronaut2007;28(1):94–8[Chinese].

26.Chen XQ,Wang F,Zhang YC,Geng Y.Application of effectiveness factors to integrated FDD and FTC of satellite attitude control systems.Acta Aeronaut Astronaut Sin2009;30(3):476–83[Chinese].

8 July 2015;revised 27 November 2015;accepted 15 December 2015

Available online 23 February 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 451 86402357.

E-mail address:cxqhit@163.com(X.Chen).

Peer review under responsibility of Editorial Committee of CJA.

Chen Xueqinreceived her B.S.degree in Automation,M.S.degree in Spacecraft Design and Ph.D degree in Control Science&Engineering from Harbin Institute of Technology in 2003,2005 and 2008,respectively,and now she is an associate professor there.Her main research interests are fault diagnosis and fault-tolerant control.

Zhang Jinxiureceived his B.S.and M.S.degree in Spacecraft Design and Ph.D degree in Aerospace Science and Technology from Harbin Institute of Technology in 2001,2003 and 2006,respectively.He worked from 2008 to 2013 as an associate professor there.From 2014 to 2015,he visited in école polytechnique fédérale de Lausanne(EPFL)Swiss Space Center.Now he is a professor of Harbin Institute of Technology from 2013.His main research interests are dynamics and control of formation flying or satellite swarm.