Obstacle avoidance for multi-missile network via distributed coordination algorithm

Zhao Jiang,Zhou Rui

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

Obstacle avoidance for multi-missile network via distributed coordination algorithm

Zhao Jiang*,Zhou Rui

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

Cooperative guidance;Distributed algorithms;Impact time;Missile guidance;Multiple missiles;Obstacle avoidance;Proportional navigation

A distributed coordination algorithm is proposed to enhance the engagement of the multi-missile network in consideration of obstacle avoidance.To achieve a cooperative interception,the guidance law is developed in a simple form that consists of three individual components for target capture,time coordination and obstacle avoidance.The distributed coordination algorithm enables a group of interceptor missiles to reach the target simultaneously,even if some member in the multi-missile network can only collect the information from nearest neighbors.The simulation results show that the guidance strategy provides a feasible tool to implement obstacle avoidance for the multi-missile network with satisfactory accuracy of target capture.The effects of the gain parameters are also discussed to evaluate the proposed approach.

1.Introduction

As the need for highly adaptive guidance and control approaches is increasing,obstacle avoidance techniques have been proposed for the unmanned aerial vehicles,1–3ground vehicles,4,5unmanned surface vehicles,6,7autonomous underwater vehicles,8,9and mobile robots.10,11Considering that the group of interceptor missiles is guided in the complex environment,the threat avoidance and geopolitical restrictions are also indispensable to the development of guidance and control systems.For this reason,some studies have recently focused on the design of the reference routes12and guidance laws13for obstacle avoidance.However,only the single interceptor missile was considered in the above work.To improve the performance in detecting the targets and penetrating the defense systems,the implement of cooperative engagement for multimissile network is required.14–17The difficult problem is an achievement of obstacle avoidance for multi-missile network with satisfactory accuracy of target capture as well as effective coordination of impact time between each member.18–20

In the current literature,many advanced cooperative guidance laws have been proposed for the multi-missile networks.The first class of approaches investigates the design of the impact-time constraints to achieve a simultaneous interception against the given target.In Ref.21,the closed form of impact time control guidance law is developed on the basis of the linear formulation,which can guide a group of missiles to the target at a desirable time.Then,the time-varying navigation gain is used to coordinate the impact time of the multi-missile net-work.22The extensions of the time-constrained guidance law are also presented to control both the impact time and impact angle.23,24The above guidance strategies typically require that the global information of time-to-go is available to each interceptor missile.For this reason,the distributed control architecture of the impact-time constraint is proposed to enhance the cooperative engagement of multiple missiles.25,26The discrete topology model is also used to feature the desired impact time using the consensus theory.27

Another class of approaches employs the leader–follower model to formulate the cooperative guidance problem for the multi-missile network.In Refs.28,29,a nonlinear state tracking controller and a state regulator are developed to solve the time-constrained guidance,respectively.Then,the consensus protocols are applied to the design of leader–follower strategy which guarantees that the impact time of each follower can converge to the leader in finite time.30To facilitate the heterogeneous multi-missile engagement,a distributed leader–follower model is proposed on the basis of proportional navigation(PN)guidance law.31Furthermore,the virtual leader scheme is also employed to achieve the impact time control by transforming the constrained guidance problem to the nonlinear tracking problem.32

Although the aforementioned design of the impact-time constraints21–27and leader–follower strategies28–32have promoted the development of the coordination algorithms for the multi-missile networks,the obstacle avoidance is not taken into account in these cooperative guidance approaches.Therefore,this paper presents an extension of the PN-based distributed guidance algorithm to enhance the engagement of the multi-missile network in consideration of obstacle avoidance.The contribution of the manuscript is summarized as follows:(1)the PN-based guidance law is developed in a simple form that consists of three individual components for target capture,time coordination and obstacle avoidance;(2)each member in the multi-missile network only requires the information of time-to-go from neighbors to perform a cooperative engagement;(3)the obstacle avoidance is achieved with satisfactory accuracy of target capture as well as effective coordination of impact time.

The rest of paper is organized as follows.Section 2 presents the basic assumptions and the engagement geometry.Section 3 describes the formulation of cooperative strategy in detail.In Section 4,the feasibility of the proposed guidance law is demonstrated by numerical simulation.Section 5 presents the performance evaluation by discussing the effect of gain parameters.Finally,concluding remarks are presented in Section 6.

2.Preliminaries

2.1.Basic assumptions

To simplify the nonlinear dynamics of the missile-target engagement,the pursuit situation in planar plane is considered in this paper.We assume some common conditions in the following part to facilitate the formulation of distributed coordination algorithm for the multi-missile network.

(1)Both the interceptor missile and the target are considered as the geometric points in the planar plane.

(2)The seeker and autopilot dynamics of each interceptor missile are much faster in comparison with the guidance loop.

(3)The velocity of each interceptor missile is constant and the acceleration input only changes its direction.

2.2.Engagement geometry

Suppose thatnmissiles participate in the multi-missile network to intercept a stationary target simultaneously.Under the prescribed assumptions,the two-dimensional geometry on manyto-one engagement is depicted in Fig.1.Let Midenote each interceptor missile and T denote the target,and then,the pursuit situation can be described by the following equations of motion33,34

where the subscript(i=1,2,...,n)represents each member in the multi-missile network;riis the missile-to-target range;Viis the total velocity of each missile;λiis the line-of-sight angle;the terms γiand θirepresent the heading angles in the inertial reference frame and line-of-sight frame,respectively;the acceleration command is defined asAi.

The problem studied herein is to find the coordination algorithm that can guide the group of missiles to the given target at the same time without obstacle collision,even if the initial conditions of each member are different.

3.Distributed coordination algorithm

Based on the traditional PN guidance law,this section focuses on the design of the coordination algorithm for the multimissile network in the distributed formulation.The proposed cooperative guidance law consists of three individual components as

where the termsApi,AξiandAaiare used for the target capture,time coordination and obstacle avoidance,respectively.

Fig.1 Geometry on many-to-one engagement.

The PN componentApiis derived from the traditional PN guidance law in the form of33

whereNiis the navigation constant.

In order to coordinate the impact time of each member in the multi-missile network,the componentAξiis included into the proposed coordination algorithm Eq.(2)which has a simple form as follows26:

whereKξis the gain parameter.The term ξi(t)represents the relative error of the time-to-go between each missile:

where the estimation of the time-to-go for each membertgo，i（t）in the multi-missile network is given in the form of

Note that,the termAξi→ 0 m/s2asri(t)→ 0 km if ξi(t)→0 s asri(t)→0 km,i.e.,the effect of the coordination componentAξiwill be weakened when the relative error of the timeto-go gradually decreases as the group of missiles approach the given target.To guide the interceptor missiles to the target at a same time,the design of the coordination variabletgo，i（t）will be discussed in the following part.

The centralized coordination algorithms usually consider the case that each missile communicates with all the other members in the multi-missile network.However,the guidance laws would be out of work when some interceptor missile is only able to obtain the effective information from its nearest neighbors.Therefore,it is necessary to select the coordination variabletgo，i（t）in the distributed formulation for an agreement on the impact time.Fig.2 illustrates an example of the communication limit in the multi-missile network.

As shown in Fig.2,the effective communication region of each missile is marked withSi,in which Mican obtain the information of the time-to-go from its neighbors.Thus,there are totallyncommunication regions with the group of missiles.Considering the limit of these communication regions,the coordination variabletgo，i（t）in the componentAξiis defined in distributed form as

wheresiis the total number of the missiles in the regionSi.It also means that Mican obtain the information of the time-togo from itssi–1 neighbors in the distributed communication regions.Thus,the componentAξiwill try to adjust the timeto-go of each member in the multi-missile network for a simultaneous arrival.However,the distributed design does not reduce the relative time-to-go error of the whole multimissile network,but reduces the error of each small group.Note that,the limit of the communication region is actually determined by the performance of the communication systems.In the current literature,the distance between interceptor missiles is typically used to represent the communication limit.Therefore,the neighboring missiles are also determined by the relative distance between each missile in this paper.

The third componentAaifor obstacle avoidance is based on the simple design of the potential function in the form of

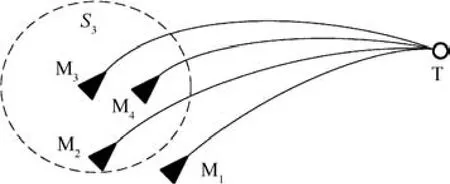
Fig.2 Communication limit in multi-missile network.

whereKais the gain parameter;the termRis the radius of the obstacle;Lirepresents the distance between the obstacle and each interceptor missile.As shown in Fig.3,the circleshaped obstacleOis used herein because any irregularly shaped obstaclesO1andO2can be simply replaced with it.

Note that,the angle αi∈ [-π/2,+π/2]is defined in the lineof-sight frame with respect to the center of the obstacle.It can be found that the componentAaimainly depends on the distanceLiand heading angle αi.To be specific,the magnitude of the input componentAaigradually increases as|Li-R|→ 0 km and|αi|→ 0°,whereas some larger|Li-R|and|αi|result in a decrease in the magnitude of the acceleration.

Thus,the complete distributed coordination algorithm for the multi-missile network can be given by Eq.(9)on the basis of the three components.The effect of target capture is determined by the PN componentApithat continues during the entire engagement.The coordination componentAξiwill dominate the guidance algorithm Eq.(9)when the time-to-go error of the multi-missile network increases.The third componentAaiis mainly used for the obstacle avoidance and it comes into effect as the interceptor missiles approach towards the obstacle.The integration of the three components leads to a trade-off in order to achieve the obstacle avoidance with satisfactory accuracy of target capture and effective coordination of impact time.

The improved coordination algorithm is quite easy to be implemented due to the simple design in the form of Eq.(9).The performance evaluation of the proposed cooperative guidance law will be presented in the following section.

4.Numerical simulations

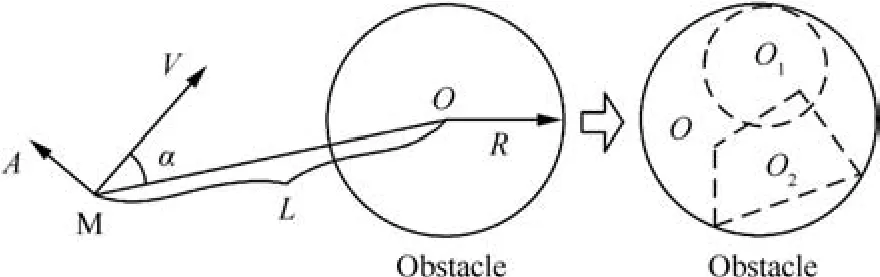
Fig.3 Geometry on interceptor missile for obstacle avoidance.

The numerical simulation is performed in a scenario of simultaneous arrival to evaluate the proposed distributed algorithm Eq.(9).Suppose that a group of three missiles participate in the multi-missile network to intercept the given target at(0,0)km with different initial conditions as shown in Table 1.The limit of the acceleration is set to be 5.0×9.81 m/s2and the navigation constant,3.0,for each interceptor missile.The gainKais set to be 20 and the gainKξis set to be 30/(r0tgo0),wherer0is the mean value of the initial missile-to-target ranges andtgo0is the mean value of the initial time-to-go estimations.

As shown in Fig.4,a simple communication topology is selected for the multi-missile network,in which M1and M3can only obtain the information of time-to-go from the neighbor M2.Thus,the coordination variables for the group of three missiles are expressed as

where the total numbers of missiles in regionsSi(i=1,2,3)ares1=2,s2=3 ands3=2,respectively.

Figs.5 and 6 show the numerical results of the distributed coordination algorithm.Case 1 demonstrates the results of the simplified guidance law without componentAai,whereas the results of the complete coordination algorithm Eq.(9)are illustrated by Case 2.In Case 1,the ground tracks and the time-togo of the multi-missile network show that the guidance law withoutAaican drive the group of three missiles to simultaneously intercept the target at 86.18 s.However,M3cannot fly round the given obstacle at(-14,5)km with a radius of 2 km.In contrast,the distributed coordination algorithm Eq.(9)succeeds in obstacle avoidance and a simultaneous arrival within a dispersion of 0.1 s.Note that the final impact time increases to 94.13 s since the group of missiles move further rounds to avoid the given obstacle.

Table 1 Initial conditions of multi-missile network.

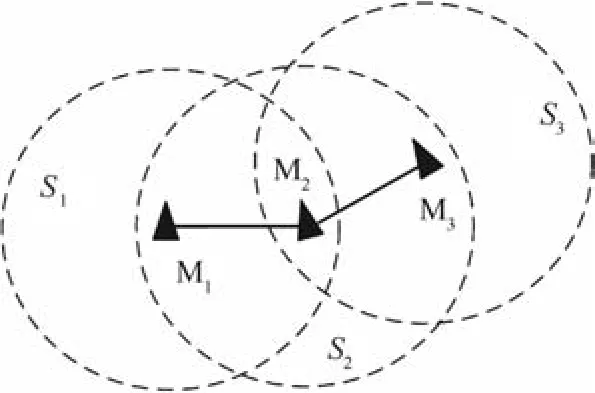
Fig.4 Communication topology for multi-missile network.

Fig.5 Ground tracks of interceptor missiles against a stationary target.

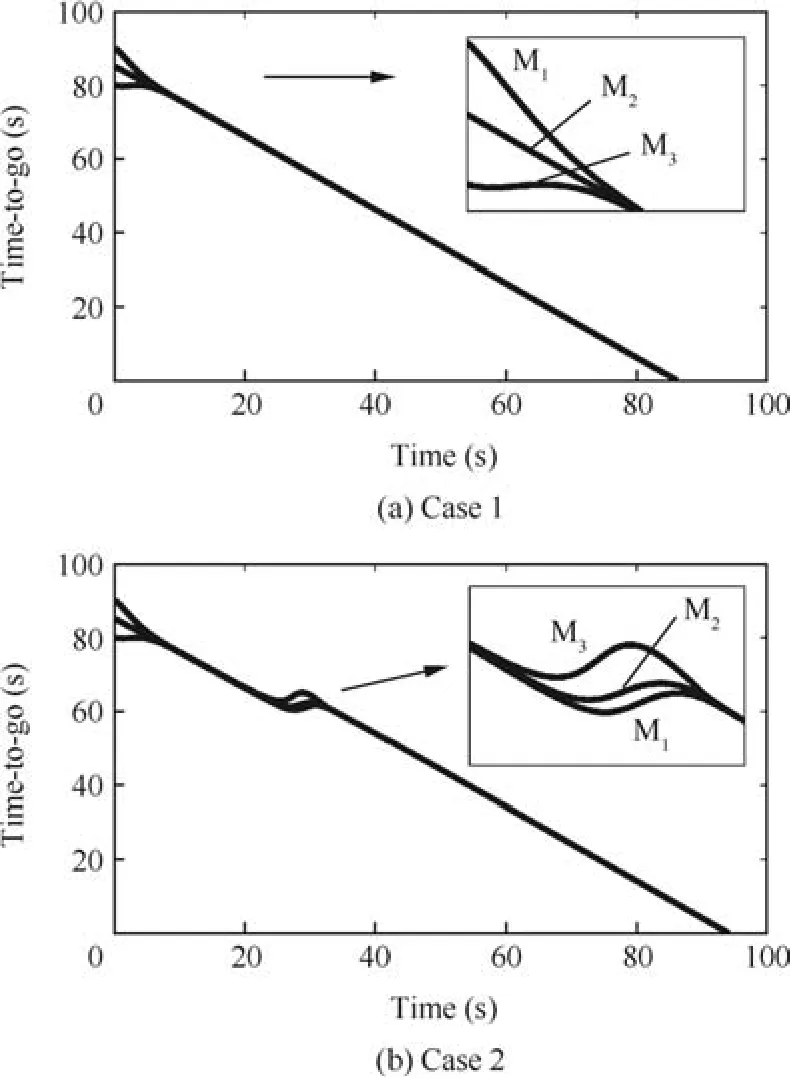
Fig.6 Times-to-go of interceptor missiles against a stationary target.

5.Discussion

5.1.Effects of gain parameters

Regarding the effectiveness of the cooperative guidance law Eq.(9),the componentAξifor coordination of impact time and the componentAaifor obstacle avoidance are largely determined by the gain parametersKξandKa.Therefore,a proper selection of these gains may guarantee that the multimissile network achieves obstacle avoidance and a satisfactory simultaneous arrival.In this part,the effects of gain parametersKξandKaare discussed through some examples.

First,we find that the convergence rate of the impact time is mainly influenced by the gain parameterKξ.Fig.7 presents the numerical results of the time-to-go for a group of three interceptor missiles,in which the gain parameterKξis set to be 20/(r0tgo0),30/(r0tgo0),40/(r0tgo0)and 50/(r0tgo0),respectively.It is quite clear that the time-to-go of the multi-missile network has the fastest convergence rate with gainKξ=50/(r0tgo0).In contrast,it becomes slower as the gain gradually decreases toKξ=20/(r0tgo0).The simulations demonstrate that a selection of gain parameterKξbetween 20 and 50 generally result in better performance of the coordination of impact time.

Further,we examine the effect of the gain parameterKaby another example.Fig.8 presents the numerical results of the ground tracks for the multi-missile network,in which the gainKais set to 10(dash-dot),20(dot),30(dash)and 40(solid),respectively.It is found that the group of missiles move earlier and further rounds to avoid the obstacle as the gain increases fromKa=10 toKa=40.As shown in Fig.9,the control effort of the interceptor missiles(solid for M1,dash for M2and dot for M3)is much lower when a larger gainKais chosen for componentAai.The simulations also suggest that the proper selection of the gain parameterKabetween 10 and 40 is able to meet the requirement for satisfactory obstacle avoidance.

Fig.7 Effect of gain parameter Kξon times-to-go.

Fig.8 Effect of gain parameter Kaon ground tracks.

5.2.Maneuvering target

In this part,the scenario of cooperative engagement against a maneuvering target is used to evaluate the proposed coordination algorithm.The same initial conditions are selected as those in Section 4.Suppose that the velocity and acceleration of the target are set to constant values,i.e.,VT=100 m/s andAT=-2.0×9.81 m/s2,respectively.The initial heading angle of the target with respect to the inertial reference frame is set to be 60°.

Figs.10 and 11 illustrate the simulation results of the cooperative engagement against the maneuvering target.Cases 3 and 4 demonstrate the coordination algorithm without componentAaiand the complete coordination algorithm Eq.(9),respectively.It can be found that each member in the multi-missile network intercepts the maneuvering target with effective coordination of impact time.The obstacle avoidance is also achieved using the proposed guidance approach.Note that the final impact time is increasing since the head-pursuit guidance is performed in this scenario.

Fig.9 Effect of gain parameter Kaon control effort.

Fig.10 Ground tracks of interceptor missiles against a maneuvering target.

5.3.Size of obstacle

Regarding the effect of the obstacle size in the coordination algorithm,another numerical simulation is performed in this part.Some different obstacle sizes(R=2 km,3 km,4 km and 5 km)are selected in the scenario of the cooperative engagement.The same initial conditions are selected as those in Section 4.

Fig.12 presents the ground tracks of the interceptor missiles.It is shown that the obstacle avoidance can be achieved using the proposed guidance law even though the size of the obstacle is up to 5 km.The coordination of the impact time is effective with satisfactory accuracy of target capture.Fig.13 illustrates the effect of the obstacle size on the acceleration and the time-to-go.It can be found that a larger size of the obstacle typically results in the earlier saturation of the control effort.The time-to-go of the multi-missile network also increases with a larger size of obstacle.

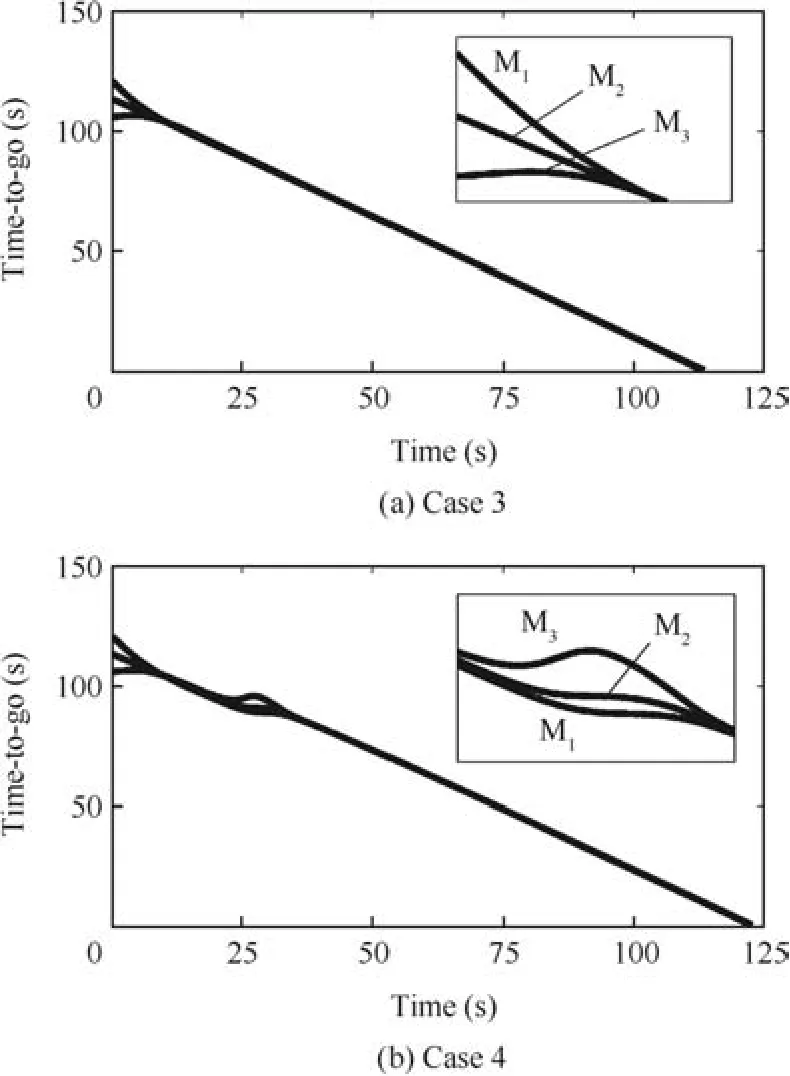
Fig.11 Times-to-go of interceptor missiles against a maneuvering target.

6.Conclusions

In this paper,a distributed coordination algorithm is proposed in which both the obstacle avoidance and the limited communication region among interceptor missiles are taken into account.

(1)The proposed guidance law takes a simple form on the basis of the traditional PN algorithm.It enables a simultaneous arrival even if some interceptor missiles can only collect the information from nearest neighbors.

(2)The simulation results show that the proper selection of gain parameterKacan guarantee the obstacle avoidance with satisfactory accuracy of target capture.The convergencerateofimpacttimeisdeterminedbyanothergainKξ.

(3)The distributed coordination algorithm is typically effective for the common size of obstacle.It also demonstrates that the cooperative interception against maneuvering target can also be achieved using the proposed algorithm.

Fig.13 Effect of obstacle size on acceleration and time-to-go.

Acknowledgments

This study was co-supported by the National Natural Science Foundation of China(Nos.61273349 and 61175109)and the Aeronautical Science Foundation of China (Nos.2014ZA18004 and 2013ZA18001).

1.Cruz GS,Encarnacao PM.Obstacle avoidance for unmanned aerial vehicles.J Intell Rob Syst2012;65(1–4):203–17.

2.Raja RG,Chawla C,Padhi R.Dynamic inversion-based nonlinear aiming point guidance of unmanned aerial vehicles for reactive obstacle avoidance.Unmanned Systems2013;1(2):259–75.

3.Zhao J,Zhou R.Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints.Chin J Aeronaut2013;26(6):1544–53.

4.Ferrara A,Vecchio C.Collision avoidance strategies and coordinated control of passenger vehicles.Nonlinear Dyn2007;49(4):475–92.

5.Sezer V,Gokasan M.A novel obstacle avoidance algorithm:Follow the gap method.Robot Auton Syst2012;60(9):1123–34.

6.Campbell S,Naeem W,Irwin GW.A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidancemanoeuvres.AnnRevControl2012;36(2):267–83.

7.Naeem W,Irwin GW,Yang A.COLREGs-based collision avoidance strategies for unmanned surface vehicles.Mechatronics2012;22(6):669–78.

8.Wu XP,Feng ZP,Zhu JM,Allen R.Line of sight guidance with intelligent obstacle avoidance for autonomous underwater vehicles.Proceedings of 2006 OCEANS;Sep 18–21;Boston(MA).Piscataway(NJ):IEEE Press;2006.p.1–6.

9.Fang MC,Wang SM,Wu MC,Lin YH.Applying the self-tuning fuzzy control with the image detection technique on the obstacleavoidance for autonomous underwater vehicles.Ocean Eng2015;93(1):11–24.

10.Korayem MH,Zehfroosh A,Tourajizadeh H,Manteghi S.Optimal motion planning of nonlinear dynamic systems in the presence of obstacles and moving boundaries using SDRE:Application on cable-suspended robot.Nonlinear Dyn2014;76(2):1423–41.

11.Sgorbissa A,Zaccaria R.Planning and obstacle avoidance in mobile robotics.Robot Auton Syst2012;60(4):628–38.

12.Zhao J,Zhou SY,Zhou R.Distributed time-constrained guidance using nonlinear model predictive control.Nonlinear Dyn2016.http://dx.doi.org/10.1007/s11071-015-2578-z.

13.Wang GH,Sun XF,Zhang LP,Lyu C.Saturation attack based route planning and threat avoidance algorithm for cruise missiles.J Syst Eng Electron2011;22(6):948–53.

14.Zhao J,Zhou R,Jin XL.Progress in reentry trajectory planning for hypersonic vehicle.J Syst Eng Electron2014;25(4):627–39.

15.Liu G,Lao SY,Tan DF,Zhou ZC.Research status and progress on anti-ship missile path planning.Acta Automat Sin2013;39(4):347–59 Chinese.

16.Zhao J,Zhou R.Particle swarm optimization applied to hypersonic reentry trajectories.Chin J Aeronaut2015;28(3):823–31.

17.Bao W.Present situation and development tendency of aerospace control techniques.Acta Automat Sin2013;39(6):697–702 Chinese.

18.Shin HS.Study on cooperative missile guidance for area air defence[dissertation].Cranfield:Cranfield University;2012.

19.Zhao J,Zhou R.Pigeon-inspired optimization applied to constrained gliding trajectories.Nonlinear Dyn2015;82(4):1781–95.

20.Zhao J,Zhou R,Dong Z.Three-dimensional cooperative guidance laws against stationary and maneuvering targets.Chin J Aeronaut2015;28(4):1104–20.

21.Jeon IS,Lee JI,Tahk MJ.Impact-time-control guidance law for anti-ship missiles.IEEE Trans Control Syst Technol2006;14(2):260–6.

22.Jeon IS,Lee JI,Tahk MJ.Homing guidance law for cooperative attack of multiple missiles.J Guid Control Dyn2010;33(1):275–80.

23.Zhang YA,Ma GX,Liu AL.Guidance law with impact time and impact angle constraints.Chin J Aeronaut2013;26(4):960–6.

24.Lee JI,Jeon IS,Tahk MJ.Guidance law to control impact time and angle.IEEE Trans Aerosp Electron Syst2007;43(1):301–10.

25.Zhao SY,Zhou R.Cooperative guidance for multimissile salvo attack.Chin J Aeronaut2008;21(6):533–9.

26.Zhao J,Zhou R.Unified approach to cooperative guidance laws against stationary and maneuvering targets.Nonlinear Dyn2015;81(4):1536–47.

27.Peng C,Liu X,Wu S,Li M.Consensus problems in distributed cooperative terminal guidance time of multi-missiles.Control Decision2010;25(10):1557–66 Chinese.

28.Zhang YA,Ma GX,Wang XP.Time cooperative guidance for multi-missiles:A leader-follower strategy.Acta Aeronaut Astronaut Sin2009;30(6):1109–18 Chinese.

29.Wang X,Hong X,Lin H.A method of controlling impact time and impact angle of multiple-missiles cooperative combat.J Ball2012;24(2):1–6 Chinese.

30.Sun XJ,Zhou R,Hou DL,Wu J.Consensus of leader–followers system of multi-missile with time-delays and switching topologies.Optik2014;125(3):1202–8.

31.Zou L,Ding Q,Zhou R.Distributed cooperative guidance for multiple heterogeneous networked missiles.J Beijing Uni Aeronaut Astronaut2010;23(1):103–8 Chinese.

32.Zhao SY,Zhou R,Wei C,Ding QX.Design of time-constrained guidance laws via virtual leader approach.Chin J Aeronaut2010;23(1):103–8.

33.Ha IJ,Hur JS,Ko MS,Song TL.Performance analysis of PNG laws for randomly maneuvering targets.IEEE Trans Aerosp Electron Syst1990;26(5):713–21.

34.Zhou D,Qu P,Sun S.A guidance law with terminal impact angle constraint accounting for missile autopilot.J Dyn Syst Measur Control2013;135(5):051009-1–051009-10.

23 July 2015;revised 31 August 2015;accepted 30 September 2015

Available online 23 February 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 10 82316849.

E-mail addresses:jzhao@buaa.edu.cn(J.Zhao),zhr@buaa.edu.cn(R.Zhou).

Peer review under responsibility of Editorial Committee of CJA.

Zhao Jiangis currently a Ph.D.candidate in guidance,navigation and control from Beihang University,Beijing,China.His area of expertise includes autonomous flight control and guidance,constrained trajectory optimization,and flight mission planning.

Zhou Ruiis currently a professor in guidance,navigation,and control from Beihang University,Beijing,China.His area of expertise includes autonomous flight control and guidance,constrained trajectory optimization and flight mission planning.