A new SINS/GPS sensor fusion scheme for UAV localization problem using nonlinear SVSF with covariance derivation and an adaptive boundary layer

Friz Outmzirt,Fu Li,Lin Yn,Adelkrim Nemr

aSchool of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

bSchool of Control and Automation,Ecole Militaire Polytechnique,Algiers 16111,Algeria

A new SINS/GPS sensor fusion scheme for UAV localization problem using nonlinear SVSF with covariance derivation and an adaptive boundary layer

Fariz Outamazirta,*,Fu Lia,Lin Yana,Abdelkrim Nemrab

aSchool of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

bSchool of Control and Automation,Ecole Militaire Polytechnique,Algiers 16111,Algeria

Adaptive smoothing boundary layer;Autonomous airborne navigation;GPS;Smooth variable structure filter(SVSF);Strapdown inertial navigation system(SINS)

The state estimation strategy using the smooth variable structure filter(SVSF)is based on the variable structure and sliding mode concepts.As presented in its standard form with a fixed boundary layer limit,the value of the boundary layer width is not precisely known at each step and may be selected based on a priori knowledge.The boundary layer width reflects the level of uncertainty in the model parameters and disturbance characteristics,where large values of the boundary layer width lead to robustness without optimality and small values of the boundary layer width provide optimality with poor robustness.As a solution and to overcome these limitations,an adaptive smoothing boundary layer is required to achieve greater robustness and suitable accuracy.This adapted value of the boundary layer width is obtained by minimizing the trace of the a posteriori covariance matrix.In this paper,the proposed new approach will be considered as another alternative to the extended Kalman filters(EKF),nonlinearH∞and standard SVSF-based data fusion techniques for the autonomous airborne navigation and self-localization problem.This alternative is based on strapdown inertial navigation system(SINS)and GPS data using the nonlinear SVSF with a covariance derivation and adaptive boundary layer width.Furthermore,the full mathematical model of the SINS/GPS navigation system considering the unmanned aerial vehicle(UAV)position,velocity and Euler angle as well as gyro and accelerometer biases will be used in this paper to estimate the airborne position and velocity with better accuracy.ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access

1.Introduction

Unmanned aerial vehicles(UAVs)receive increasing interest in strategic and tactical defense programs1as well as for civilian application.UAVs require accuracy and advanced autonomyto accomplish difficult missions in harsh environments.The challenge to improve the accuracy of the UAV localization performance can be achieved by combining navigation data from different sensors.2The design and development of integrated navigation systems is used for these autonomous vehicles to take advantage of the complementary attributes of two or more navigation sensors,which yield integrated systems that are more accurate and reliable.Inertial sensors,such as the strapdown inertial navigation system(SINS),are able to deliver the position,velocity and attitude of the UAV with high accuracy over the short term with relatively low noise but tend to drift over time.3In contrast,the GPS provides real-time three-dimensional position and velocity information with only random errors that do not grow unboundedly.4By making use of the synergy between the SINS and GPS throughout the filtering techniques,the fused data provide the level of localization accuracy required by UAV missions.5Non-linear filtering techniques have attracted considerable research interest over the past three decades to resolve the nonlinear filtering problems of integrated navigation,which include extended Kalman filters(EKF),6unscented Kalman filter(UKF)7and particle filter(PF).8Unfortunately,Kalman filtering and its extension typically do not guarantee satisfactory results when the model is affected by uncertainty as well as when the process and measurement equations are not affected by non-centered Gaussian noise.9However,an innovative approach known as nonlinearH∞(NH∞)has attracted great interest and continuous research attention to avoid the issues linked with modeling error and noise uncertainties,incorporating aspects of several approaches.10–17The form of NH∞developed in Refs.10,11has been used to solve the UAV localization problem using INS/GPS in.18Although the common criterion of NH∞is to ensure a bounded energy gain from the worst case to the estimator error,it is still diff icult to prescribe the level of disturbance attenuation.19

A recent breakthrough method for state estimation called the smooth variable structure filter(SVSF)was introduced to resolve the instability problems of the Kalman filter and its extended form.The SVSF is based on a variable structure control and sliding mode,which makes it robust to bounded uncertainties and can guarantee the stability given an upper bound for the uncertainties and magnitude of noises.20This new approach is presented in predictor form and can be applied to linear and nonlinear systems.20A new form of SVSF with covariancederivation wasapplied to an electrohydrostatic actuator(EHA)that is used in aerospace and was compared with the KF in Ref.21The SVSF,as presented in its standard form in Ref.21,defines the boundary layer width ψ by an upper bound on the uncertainties present in the estimation process by assuming a larger smoothing boundary subspace than what is required,which limits the gain.22Moreover,the value of ψ is not precisely known at each step but may be selected based on a priori knowledge.22Consequently,to obtain more accurate estimates,an augmented form of SVSF with an optimal variable boundary layer was proposed.22The boundary layer width ψ reflects the levels of uncertainty in the model parameters and disturbance characteristics,where large values of ψ lead to robustness without optimality and small values of ψ provide optimality with poor robustness.As a solution and to overcome these limitations,an adaptive smoothing boundary layer ψ is used to achieve greater robustness and suitable accuracy.This adapted value of ψ is obtained by minimizing the trace of the a posteriori covariance matrix.22It is very interesting to obtain an optimal time-varying strategy with this approach at each step time.The primary contribution of this paper is the development and validation of an alternative to the EKF,NH∞and standard SVSF-based data fusion techniques for autonomous airborne navigation and selflocalization problems.This alternative is based on SINS and GPS data using the nonlinear SVSF with a covariance derivation and adaptive boundary layer width.However,the full mathematical model of the SINS/GPS navigation system considering the UAV position,velocity and Euler angle,as well as the gyro and accelerometer biases,will be used here to estimate the airborne position and velocity with better accuracy.

2.SINS/GPS fusion model

2.1.Orientation

Various coordinate frames and transformations of coordinates are used in inertial navigation computation.The transformation between the various coordinate systems can be expressed by the coordinate transformation matrix.In this transformation,it will be assumed that the UAV body axes are defined as follows:thex-axis points forward,they-axis points to the right and thez-axis completes the right-hand orthogonal system by pointing downward.Three successive single-axis rotations pass through the Euler angles of roll,pitch and yaw to calculate the UAV attitude.23The navigation frame northeast–down(NED)is defined by the local earth axis with the vector pointing north,the vector pointing east and the vector pointing down along the local gravity vector.24Furthermore,in this configuration,the navigation frame is a right-handed NED.

The measurements of the acceleration and the rotation of the vehicle are completed by inertial sensors mounted in a unit called the inertial measurement unit(IMU).25The IMU grasps two orthogonal sensor triads with three accelerometers measuring the acceleration and three gyroscopes measuring the rotation rates,as indicated in Fig.1,whereax，ayandazare accelerations alongx-axis,y-axis andz-axis respectively,p，qandrthe angle rotation rates.

The transformation matrices from the body frame to the navigation frame that involve three successive single-axis rotations through the ordinary Euler anglesR（φ）,R（θ）andR（φ）,which signify the roll,pitch and yaw,respectively,5,24are given as

2.2.General relative motion equations

To calculate the Euler angle rates（˙φ，˙θ，˙φ）,we transform the rotation rates （p，q，r）from the body frame to the navigation frame as5,24

Fig.1 Diagram of mechanization process of SINS.25

2.3.General navigation equations

The ideal accelerometer measures the specific forces,which is the difference between the inertial acceleration and gravitational acceleration.23The true vehicle acceleration（˙U，˙V，˙W）is calculated in the body frame with the assumption that the IMU is at the vehicle center of the gravity5,24as

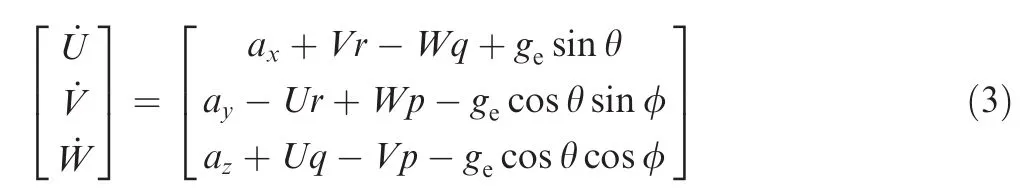
wheregeis the Earth gravity.

The derivative of the velocity is then integrated to obtain the position of the UAV.The velocity is transformed to the navigation frame and is integrated to yield the position of a vector （X，Y，Z）5,24as

2.4.Nonlinear model using Euler angles

The nonlinear model of the SINS can be defined as

where y（t）is observation;h is continuous observation model;and x is the state vector,which contains the position,velocity,Euler angles,constant random drifts in the gyros,and constant random biases in the accelerometers as

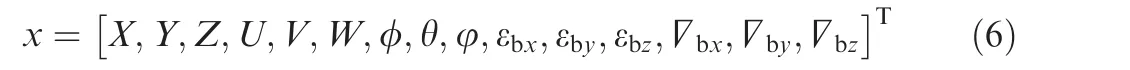
whereεbx，εbyandεbzaretheconstantrandomdriftsinthegyros and ■bx，■byand ■bzthe constant random biases in the accelerometers.12Thus,u represents the IMU outputs,where the angles’rates and accelerations5,24can be expressed as

The nonlinear SINS state model is given as

2.5.Global positioning system

The global navigation satellite systems(GNSS)consist of four main satellite technologies:the GPS developed by the United States Department of Defense(DoD);the Russian Global Orbit Navigation Satellite System (GLONASS);Galileo,belonging to the European Union and developed by the European Space Agency(ESA);and the BeiDou Navigation Satellite System(BDS),developed by the China National Space Administration(CNSA).In this paper,we use the GPS because it is well recognized.26The GPS consists of at least 24 satellites on six equally spread orbits around Earth.The six orbital planes are inclined at an angle of 55°with respect to the equator.Theorbitsarelocated approximately 20200 km above Earth’s surface.26The GPS receiver must receive the signals of at least four satellites to estimate a 3-dimensional position and provides the accurate Coordinated Universal Time(UTC).26However,the GPS satellites transmit signals at two radio frequencies called L1 and L2,which are centered at 1575.41 MHz and 1227.60 MHz,respectively.25In the precise range measurements,the pseudo random noise(PRN)used to modulate each frequency and the standard positioning service(SPS)is associated with a coarse acquisition(C/A)code.25The precise positioning service(PPS)uses the precise code(P-code).Frequency L1 is modulated by the C/A and P-codes,whereas L2 is modulated by the P-code only.25

The measurement model,which is related to the position and velocity of the UAV used in this paper,can be expressed as

3.Nonlinear H∞filter

The strength of this approach is that no statistical assumptions regarding the noise signals are required and it has been demonstrated that it is robust against un-modeled dynamic parameter variation and model reduction.27The common performance criterion of the filter is to guarantee a bounded energy gain from the worst possible disturbance to the estimation error.11In this paper,we will consider the NH∞approach developed by Einicke and White,10where the higher-order terms are not neglected and a min–max estimation problem is resolved through the typical NH∞techniques.11The extendedH∞filter is the standardH∞filter for the problem given by Einicke and White11

The measurement model is presented as

Theobservation and measurementmodelnoiseare assumed to be a zero-mean uncorrelated random sequence.28At timek,xkis the state vector of the system;ukis control vector;the random variables wkand νkrepresent the process and measurement noise,respectively;ykis the measurement vector;Qkis the process noise covariance;and Rkis the measurement noise covariance.28,29The nonlinear model and measurement model expanded as a Taylor series around the filtered and predicted estimates of^xkand^xk-1can be defined as follows5,12:

where Δfk（x）is the Jacobian offevaluated at xk-1;^xk/kis the estimated state vector at timekand^xk/k-1the predictor state;Δfw（x）is the Jacobian of f/wkevaluated at xk-1;Δhk（x）is the Jacobian of h evaluated at xk-1;and Δi（i=1，2，3）represents the higher-order terms of the Taylor series norm,which are bounded as ‖Δi‖ ≤ δi.5,30

The time update of the estimation error covariance can be defined as follows:

where Pk/kis error covariance at timek.

Then,the EKF formulation is written in the predictor–corrector scheme as follows:(1)Kalman gain

where Pk/k-1is error covariance at timekgiven all information up to timek-1.

(2)Corrected state estimate

(3)Corrected covariance matrix

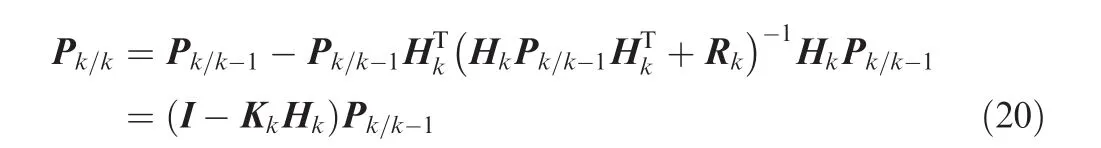
The NH∞approach is applied using the system defined in Eq.(12)in the following form:

where the additional exogenous inputs Tk,φk,Mkand ξksatisfy the following conditions11:

Eq.(21)is represented by scaling wkand νkas follows11:

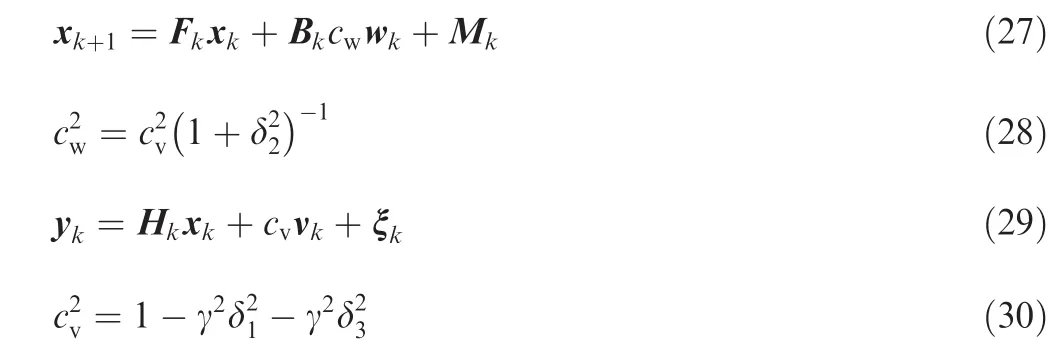
where γ is disturbance attenuation.

The NH∞algorithm steps are the same as the structure of the EKF algorithm defined in Eqs.(19)–(23),with the only difference in the formulation of the approximate error covariance correction,which is given by

where Ckis measurement matrix.

As the approach of NH∞used in this paper is based on the idea of EKF,the NH∞still suffers from the shortcoming of EKF relating to the constraint of the low linearity of the system and the errors due to the Jacobian matrix calculation.31Additionally,the difficulty of tuning parameter γ leads to controlling the tradeoff between theH∞performance and minimum variance performance.11The problem is that when the state error and process noise are considered insignificant,the NH∞reverts to EKF when γ tends to infinite.11The search for a way to circumvent these issues is the motivation to investigate a new approach to filtering based on the sliding mode,known as the SVSF.

4.Smooth variable structure filter

The first attempts to introduce the efficient estimation strategy of the VSF as a new predictor corrector were in 2002.32,33This type of estimation uses approaches based on variable structure control theory,which can guarantee stability given bounded parametric uncertainty.32Emelyanov and a number of coresearchers from the former Soviet Union34investigated the variable structure control and sliding mode control.The distinguishing feature of sliding mode control theory is that it provides a method to design a system,thus,the controlled system should have parametric uncertainty and external disturbances.35The VSF is a type of sliding mode estimator where the switching gain concept is used to keep the estimates converging in the existence subspace to true state values.22A further development of the VSF estimation results from its derivation,known as the SVSF,which was introduced in 2007.20The SVSF is model-based and has been applied to smooth nonlinear dynamic equations.36It is stable and robust to modeling uncertainties and noise,giving an upper bound on the level of un-modeled dynamics or knowledge of the level of noise.20However,the estimation error or filtering innovation is used in the classical filtering approaches as landmarks to measure their performances and accuracy.Moreover,the SVSF is endowed with a performance indicator that quantifies the degree of uncertainty and modeling error specific to each state or parameter that is being estimated.20

The present paper is part of the continuous line of research concerning the previously obtained results using the SVSF to solve the UAV localization problem.37In this paper,the architecture based on the complementary dead reckoning system(SINS)and positioning system(GPS)used to solve the UAV localization problem is shown in Fig.2.We investigate an alternative to the EKF,NH∞and standard SVSF-based data fusion techniques for the autonomous airborne navigation and self-localization problem using the full mathematical model of the SINS/GPS navigation system with the UAV position,velocity and Euler angle,as well as the gyro and accelerometer biases.

Fig.2 Scheme representing integrated navigation system based on SVSF with covariance derivation and an adaptive boundary layer.25

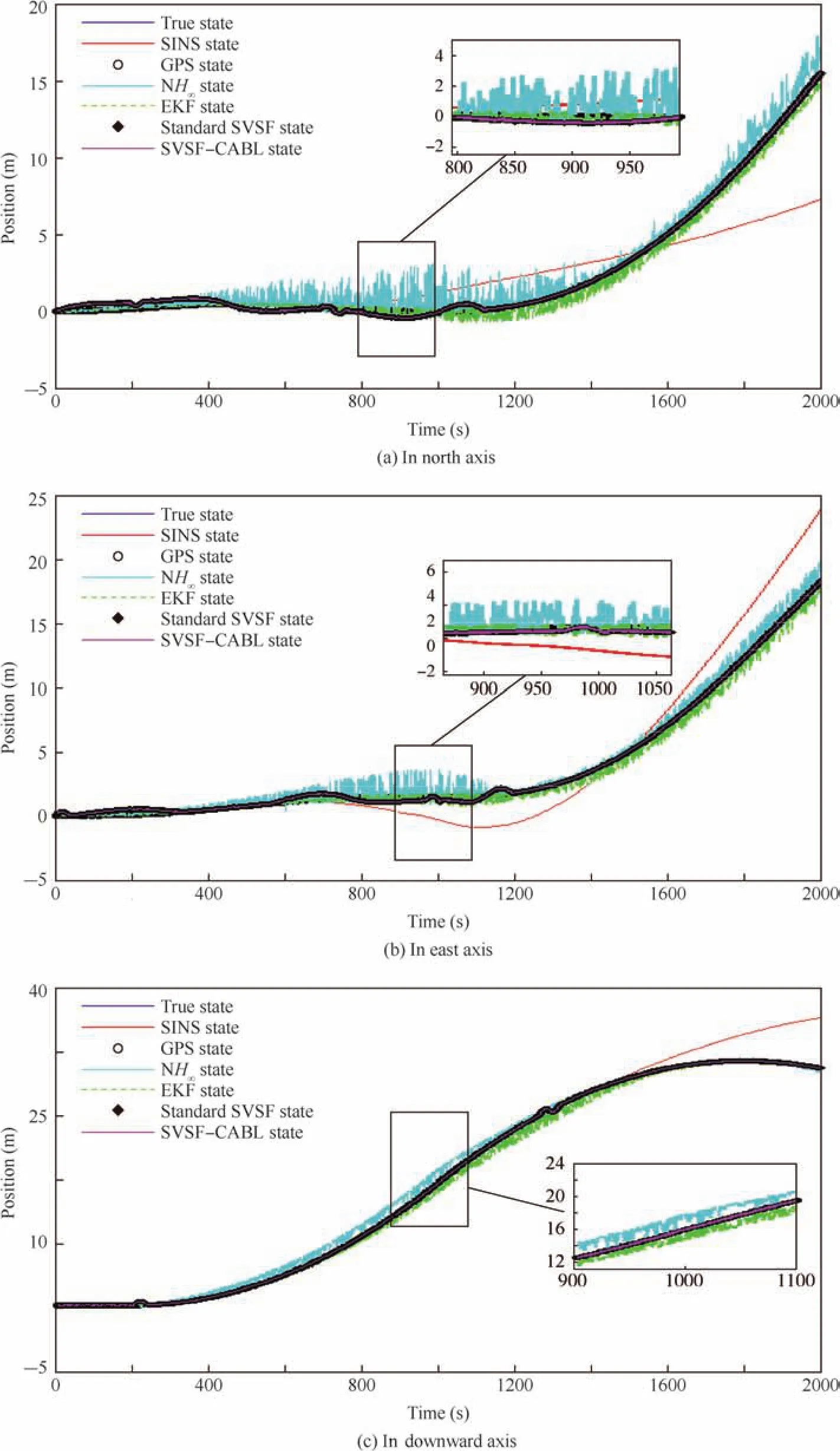
Fig.3 Estimation of airborne positions.

This alternative is based on SINS and GPS data using the nonlinear SVSF with a covariance derivation and adaptive boundary layer width.The novel estimation technique SVSF is considered to obtain a higher position and velocity accuracy while overcoming the shortcoming of the Kalman filtering techniques when modeling uncertainties are present.In the SVSF,as shown in Fig.2,the trajectory of a state variable in time is obtained through the uncertain model of the nonlinear system SINS/GPS,which is used to generate the trajectory of an estimated state.20The estimated trajectory is then enforced in the direction of the true state trajectory,in such a way that it will be in the existence subspace whereby the estimated trajectory converges to the true state.20The width of the existence subspace is unknown and is a function of the disturbances and uncertainties20as the effects of unknown gravity modeling errors,accelerometer bias and gyroscope drift.To saturate and smooth out the chattering within the subspace,an adaptive boundary layer(ψ)will be used along the sliding surface.22Following this,we summarize the main equations for different variants of the SVSF.

4.1.SVSF with covariance derivation

The SVSF presented in Ref.20does not have a covariance,which could be used to determine the optimal value of the gain.21To obtain the covariance matrix,a revised form of the SVSF was presented in Ref.21without affecting its stability.21The SVSF with covariance derivation is defined by the following equations.21

A priori state estimate is predicted using the estimated model of the system as follows:

A priori state error covariance is given by

where A is a linear system transition matrix.

A priori estimate of the measurement is given by

A priori output error estimate is calculated as

where zk+1is the measurement output.

The SVSF gain is calculated as a function of the error in the predicted output,and the smoothing boundary layer is given by

where°denotes element-by-element multiplication.

A posteriori state estimate is calculated as

A posteriori state error covariance is a function of the a priori state error covariance and the measurement model,and the measurement noise covariance is given by

where H is a linear measurement output matrix.

Fig.4 Estimation of airborne 3D trajectory.

A posteriori output error estimate is given by

4.2.SVSF with derivation of an optimal boundary layer width

In the SVSF presented in Ref.21,the boundary layer width is defined by the upper bound on modeling errors and the magnitude of noise corrupted estimation process,which could be a limiting factor of the gain,by using a larger subspace boundary and smoothing more than required.22Moreover,it was assumed that a boundary layer exists for each state trajectory estimated.22In 2011,a revised form of SVSF22was introduced,where an optimal variable boundary layer is obtained by minimizing the trace of the a posteriori covariance matrix.22The iterative process of the revised SVSF is summarized as follows.22

A priori state estimate is predicted using the estimated model of the system as Eq.(32),a priori state error covariance is the same as Eq.(33),a priori estimate of the measurement is the same as Eq.(34)and a priori output error estimate can be calculated by Eq.(35).

The boundary layer ψ is a function of the a priori state error covariance Pk+1/k,the measurement covariance Rk+1,a priori ezk+1/kand a posteriori measurement error ezk/kand the convergence rate γ,and is given by

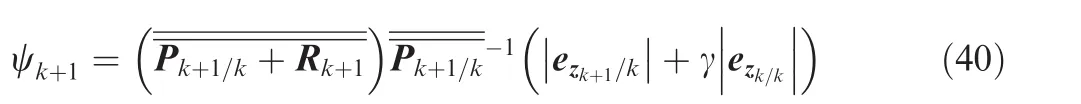
where|ezk+1/k|is the absolute value of a priori measurement error and|ezk/k|is the absolute value of a posteriori measurement errors.A posteriori state estimate is the same as Eq.(37).

The SVSF gain is calculated as a function of a priori ezk+1/kand previous a posteriori measurement error ezk/k,22and it can be calculated as

The convergence rate is γ and the boundary layer is ψ.The posteriori state error covariance is a function of a priori state error covariance,the measurement model and the measurement noise covariance,and it can be calculated by Eq.(38).A posteriori output error estimate is given by Eq.(39).

4.3.Nonlinear SVSF without covariance derivation

The optimal estimation in nonlinear systems applying Kalman filtering(KF)and its extension is achieved at the expense of stability and robustness.38The SVSF has been developed without covariance derivation and applied to linear and nonlinear systems.20The nonlinear SVSF without covariance derivation applied to the nonlinear model defined in Eq.(5)is expressed as follows.20

Fig.5 Estimation of airborne velocity.

The predicted state estimate calculated through the process model is given by

Table 1 Comparison of computation time between EKF,NH∞,standard SVSF and SVSF-CABL.

The predicted state estimate^xk+1/kobtained is used to calculate the related predicted measurement^zk+1/kas

The a priori and a posteriori output error estimates are given by

The gain is computed using a priori and a posteriori measurement errors,the smoothing boundary layer widths ψ,the convergence rate γ and the measurement matrix^H as20

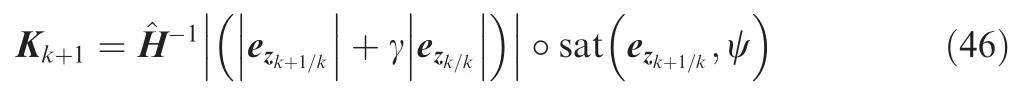
The update of the state estimates can be calculated as

4.4.Nonlinear SVSF with covariance derivation and an adaptive boundary layer

In this section,the nonlinear SVSF with covariance derivation and adaptive boundary layer(SVSF-CABL)is presented.The stability and the robustness against modeling uncertainty and noise of this new form of SVSF have been proven in Ref.21.The nonlinear SVSF-CABL algorithm is summarized as follows.

The predicted state estimates^xk+1/kcalculated through the process model are given by Eq.(42)and a priori state error covariance is calculated by Eq.(33).Then,the predicted state estimates calculated in Eq.(42)and the corresponding predicted measurements shown in Eq.(43)are used to calculate the measurement errors as Eq.(44).

wheremis the number of measurements and the saturation function defined in Eq.(48)is calculated as

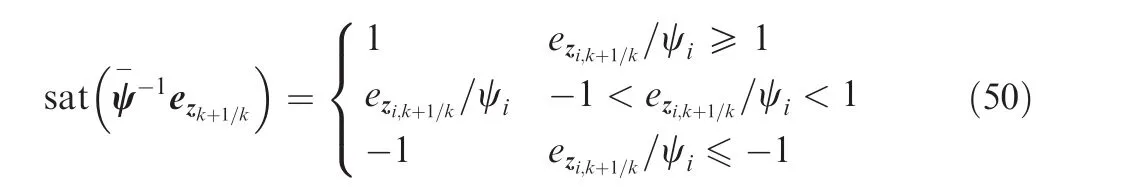
whereezi，k+1/kis the element of a priori measurement error ezk+1/k.

The gain calculated in Eq.(48)is used to update the state estimates^xk+1/k+1as Eq.(37)and the state error covariance matrix is the same as Eq.(38).

Then,the updated state estimate^xk+1/k+1is used to update the measurement estimates^zk+1/k+1as

5.Results

5.1.Estimation of airborne position

The simulation results show a comparison between the SINS,GPS,EKF,NH∞,standard SVSF and SVSF-CABL.We present the comparison to validate the proposed SVSF-CABL as an alternative to the EKF,NH∞and standard SVSF-based data fusion techniques for the autonomous airborne navigation and self-localization problem.The sampling rates used for each sensor and the update rate of the filters used in this study can be expressed as follows:

The first results show the UAV position and velocity following three axes(north axis,east axis and downward axis)using different filters.The UAV position estimation is presented in Fig.3,respectively,following the three axes.The comparison between the SINS,GPS,EKF,NH∞,standard SVSF and SVSF-CABL techniques shows that the four filters provide good performances based on a comparison with the SINS position.The EKF and NH∞filter positions exhibit some chattering around the GPS position.In contrast,the standard SVSF and SVSF-CABL are relatively similar and perform significantly better than EKF and NH∞.The SVSF-CABL provides more accurate positioning.This result is confirmed by the 3D trajectory shown in Fig.4,where the trajectories are compared with the true state.Under reduced initial conditions,including heavy nonreality,modeling errors and uncertainties,the airborne position estimated by nonlinear SVSF-CABL clearly shows its robustness and smoothness compared to the standard SVSF,EKF and NH∞.

Fig.6 True estimation error of airborne position.

Fig.7 True estimation error of airborne velocity.

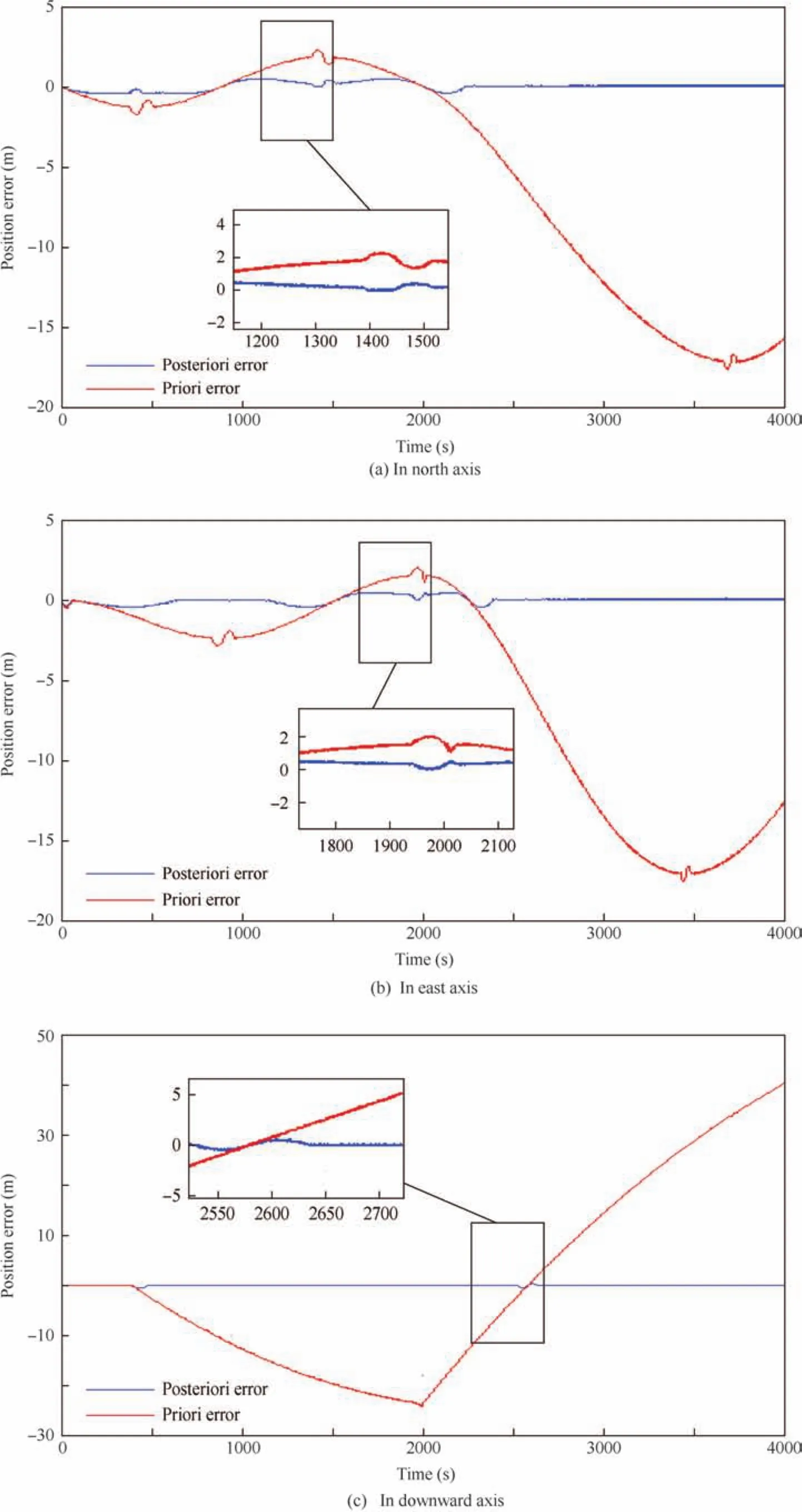
Fig.8 Estimation of a priori error and a posteriori error of SVSF-CABL for position.

Fig.9 Estimation of a priori error and a posteriori error of SVSF-CABL for velocity.

Fig.10 Estimation of airborne position using real GPS and real IMU data.

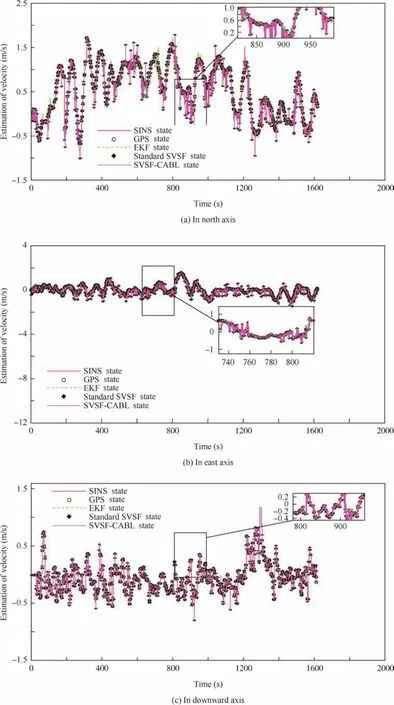
Fig.11 Estimation of airborne velocity using real GPS and real IMU data.

5.2.Estimation of airborne velocity

Fig.5 present the evolution of the UAV velocities following the north axis,east axis and downward axis,respectively.The four filters EKF,NH∞,standard SVSF and SVSFCABL maintain good precision compared to the SINS velocities,which drift with time.

Table 1 provides a comparison of the computation times between EKF,NH∞,standard SVSF and SVSF-CABL for 100 iterations.The UAV localization algorithm using the SVSF-CABL is computationally fast compared to EKF and NH∞.The SVSF-CABL enables a quicker computation time than the standard SVSF,which makes it suitable for realtime implementation.

5.3.True estimation error of airborne position and velocity

Figs.6 and 7 present the true estimation error of the airborne position and velocity following the three axes in the presence of modeling errors and uncertainties,indicating that the process and observation noises are uncorrelated zero-mean Gaussian.As seen from Figs.6 and 7,the nonlinear SVSF-CABL and standard SVSF are more accurate and provide a smaller estimation error than the EKF and NH∞filters.Moreover,the results show that the nonlinear SVSF-CABL maintains a small level of the true estimation error,without any assumption regarding the noise characteristics.

The a priori error and a posteriori error are critical for the SVSF filter convergence.Figs.8 and 9 present a comparison between the a priori error and a posteriori error of the SVSF with an adaptive boundary layer for the position and velocity following the three axes.The a posteriori error is smaller than the a priori error for position and velocity because the a priori error is based on the predicted measurement,whereas the a posteriori error is based on the true measurement.

5.4.Experimental evaluations of SVSF-CABL using real GPS and real IMU data

The results shown in Figs.10 and 11 present the estimation of the airborne position and velocity following three axes using real GPS and real IMU data.It is clear from the experimental evaluations using real GPS and real IMU data that the SVSFCABL filter maintains good accuracy compared to standard SVSF and the EKF which presents lot of chattering.These results confirm the robustness of SVSF-CABL for real scenario.The robustness of the SVSF-CABL depends highly to the wide of the boundary layer.This latter is calculated adaptively by minimizing the trace of the covariance matrix,which increases the robustness of the proposed approach.

6.Conclusions

In this paper,the proposed approach suggests the use of a nonlinear SVSF with a covariance derivation and adaptive boundary layer width(SVSF-CABL)as another alternative to the EKF,NH∞and standard SVSF-based data fusion techniques using SINS/GPS for the autonomous airborne navigation and self-localization problem.We demonstrate the performance and implementation advantages of this approach,which is more robust against modeling error and parameter uncertainty and provides accurate estimations compared with the EKF,NH∞and standard SVSF techniques.Our future research work will exploit the performances of the standard SVSF and SVSF with a covariance derivation and adaptive boundary layer to develop their hybridization using fuzzy logic.

Acknowledgement

This study was supported by the National Natural Science Foundation of China(No.61375082).

1.Craparo E,Feron E.Natural language processing in the control of unmanned aerialvehicles.ProceedingsofAIAAguidance,navigation and control conference;2004 Aug 16–19;Rhode Island.Reston:AIAA;2004.p.1–13.

2.Nemra A.Robust airborne 3D visual simultaneous localisation and mapping[dissertation].Cranfield:Cranfield University;2010.

3.Titterton D,Weston J.Strapdown inertial navigation technology.2nd ed.Herts,UK:The Institution of Engineering&Technology;2004.p.410.

4.Shin EH,El-Sheimy N.Accuracy improvement of low cost INS/GPS for land applications.Proceedings of the 2002 national technical meeting of the institute of navigation;2002 Jan 28–30;San Diego(CA).Manassas(VA):The Institute of Navigation(ION);2002.p.146–57.

5.Nemra A,Aouf N.Robust INS/GPS sensor fusion for UAV localization using SDRE nonlinear filtering.IEEE Sens J2010;10(4):789–98.

6.Yi Y,Grejner-Brzezinska DA.Tightly-coupled GPS/INS integration using unscented Kalman filter and particle filter.Proceedings of the 19th international technical meeting of the satellite division of theinstituteofnavigation;2006 Sep 26–29;FortWorth(TX).Manassas(VA):The Institute of Navigation(ION);2006.p.2182–91.

7.Zhang P,Gu J,Milios EE,Huynh P.Navigation with IMU/GPS/digital compass with unscented Kalman filter.Proceedings of 2005 IEEE international conference on mechatronics and automation;2005;Niagara Falls(Ont).Piscataway(NJ):IEEE Press;2005.p.1497–502.

8.Radon-Nykodim R,Del Moral P,Monin A,Salut G.Optimal nonlinear filtering in GPS/INS integration.IEEE Trans Aerosp Electron Syst1997;33(3):835–50.

9.Garcia G,Tarbouriech S,Peres PLD.Robust Kalman filtering for uncertain discrete-time linear systems.Int J Robust Nonlin2003;13(13):1225–38.

10.Einicke GA,White LB.The extendedH∞filter–A robust EKF.Proceedings of 1994 IEEE international conference on acoustics,speech,andsignalprocessing;1994 Apr 19–22;Adelaide(SA).Piscataway(NJ):IEEE Press;1994.p.181–4.

11.Einicke GA,White LB.Robust extended Kalman filtering.IEEE Trans Signal Process1999;47(9):2596–9.

12.Outamazirt F,Fu L,Lin Y,Nemra A.Autonomous navigation system using a fuzzy adaptive nonlinearH∞filter.Sensors2014;14(9):17600–20.

13.Geromel JC,de Oliveira MC,Bernussou J.Robust filtering of discrete-time linear systems with parameter dependent Lyapunov functions.Proceedings of the 38th IEEE conference on decision and control;1999 Dec;Phoenix(Arizona).Piscataway(NJ):IEEE Press;2002.p.570–5.

14.Qiu J,Feng G,Yang J.Robust mixedH2/H∞filtering design for discrete-time switched polytopic linear systems.IET Control Theory Appl2008;2(5):420–30.

15.Duan ZS,Zhang JX,Zhang CS,Mosca E.RobustH2andH∞filtering for uncertain linear systems.Automatica2006;42(11):1919–26.

16.Gao HJ,Meng XY,Chen TW.A parameter-dependent approach to robust filtering for time-delay systems.IEEE Trans Autom Control2008;53(10):2420–5.

17.Dong HL,Wang ZD,Ho DWC,Gao HJ.Robust filtering for Markovian jump systems with randomly occurring nonlinearities and sensor saturation:the finite-Horizon case.IEEE Trans Signal Process2011;59(7):3048–57.

18.Abdelkrim N,Aouf N,Tsourdos A,White B.Robust nonlinear filtering for INS/GPS UAV localization.Proceedings of 2008 16th mediterraneanconferenceoncontrolandautomation;2008 Jun 25–27;Ajaccio,France.Piscataway(NJ):IEEE Press;2008.p.695–702.

19.Liu L,Zhang H,Xiong K.Adaptive robust extended Kalman filter for nonlinear stochastic systems.IET Control Theory Appl2008;2(3):239–50.

20.Habibi S.The smooth variable structure filter.Proc IEEE;2007;95(5):1026–59.

21.Gadsden SA,Habibi SR.A new form of the smooth variable structure filter with a covariance derivation.Proceedings of the 49th IEEE conference on decision and control(CDC);2010 Dec 15–17;Atlanta(GA).Piscataway(NJ):IEEE Press;2010.p.7389–94.

22.Gadsden SA,Sayed MEL,Habibi SR.Derivation of an optimal boundary layer width for the smooth variable structure filter.Proceedings of 2011 American control conference;2011 Jun 29–Jul 01;San Francisco(CA).Piscataway(NJ):IEEE Press;2011.p.4922–7.

23.Siouris GM.Aerospace avionics systems:A modern synthesis.New York:Academic Press;1993.p.21–2.

24.Ro¨nnba¨ck S.Developement of a INS/GPS navigation loop for an UAV[dissertation].Lulea˚,Sweden:Lulea˚University of Technology;2000.

25.Noureldin A,KaramatTB,Georgy J.Fundamentalsof inertialnavigation,satellite-basedpositioningandtheir integration.Berlin:Springer Verlag;2013.p.14.

26.Schumacher A.Integration of a GPS aided strapdown inertial navigation system for land vehicles[dissertation].Stockholm,Sweden:Royal Institute of Technology;2006.

27.Wang ZD,Yang FW,Liu XH.Robust filtering for systems with stochastic non-linearities and deterministic uncertainties.Proc Inst Mech Eng I J Syst Control Eng2006;220:171–82.

28.Zhang N,Wunsch DC.An extended Kalman filter(EKF)approach on fuzzy system optimization problem.Proceedings of the 12th IEEE international conference on fuzzy systems;2003 May 25–28.Piscataway(NJ):IEEE Press;2003.p.1465–70.

29.Shaked U,Berman N.H∞nonlinear filtering of discrete-time processes.IEEE Trans Signal Process1995;43(9):2205–9.

30.Simon D.Optimal state estimation:Kalman,H-infinity,and nonlinear approaches.Hoboken(NJ):John Wiley&Sons,Inc.;2006.p.377.

31.Li WL,Jia YM.H-Infinity filtering for a class of nonlinear discrete-time systems based on unscented transform.Signal Process2010;90(12):3301–7.

32.Habibi SR,Burton R.The variable structure filter.J Dyn Syst Meas Control2003;125(3):287–93.

33.Habibi S,Burton R,Chinniah Y.Estimation using a new variable structure filter.Proceedings of 2002 American control conference.Piscataway(NJ):IEEE Press;2002.p.2937–42.

34.Hung JY,Gao W,Hung JC.Variable structure control:A survey.IEEE Trans Ind Electron1993;40(1):2–22.

35.Wong CC,Chang SY.Parameter selection in the sliding mode control design using genetic algorithms.Tamkang J Sci Eng1998;1(2):115–22.

36.Gadsden SA,Dunne D,Habibi SR,Kirubarajan T.Comparaison of extended and unscented Kalman,particle,and smooth variable structure fitlers on a bearing-only target tracking problem.SPIE Opt Eng Appl2009;7445:74450B-1-13.

37.Outamazirt F,Fu L,Lin Y,Nemra A.Solving the UAV localization problem using a smooth variable Structure filtering.Proceedings of 2015 IEEE aerospace conference;2015 Mar 7–14;Big Sky(Montana).Piscataway(NJ):IEEE Press;2015.p.1–12.38.Gadsden SA.Smooth variable structure filtering:Theory and applications[dissertation].Hamilton:McMaster University;2011.39.Gadsden SA,Dunne D,Habibi SR,Kirubarajan T.Combined particle and smooth variable structure filtering for nonlinear estimation problems.Proceedings of the 14th international conference on information fusion;2011 Jul 5–8;Chicago(IL).Piscataway(NJ):IEEE Press;2011.p.1552–8.

2 July 2015;revised 21 August 2015;accepted 30 September 2015

Available online 23 February 2016

article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 10 82317306.

E-mail address:outamazirt.fariz@yahoo.fr(F.Outamazirt).

Peer review under responsibility of Editorial Committee of CJA.

Fariz Outamazirtreceived the M.E.degree in control systems from the Department of Control,Polytechnic Military School,Algeria,in 2002 and M.S.in Space Science and Technology from Regional Center for Space Science and Technology(CRASTE-LF),Kingdom of Morocco,in 2004.He is currently pursuing a Ph.D.degree at the Department of Automation Science and Electrical Engineering,Beihang University,Beijing,China.Hiscurrentresearch interestsareautonomous navigation,information fusion and spacecraft guidance.

Fu Lireceived her B.S.,M.S.and Ph.D.degrees in Control Science and Engineering from Northwestern Polytechnical University in 1991,1994 and 1997,respectively.Now she is professor in School of Automation Science and Electrical Engineering,Beihang University,China.She visited Purdue University in West Lafayette,Indiana,USA,as a visiting scholar for 16 months during 2011–2012.Her research interests span the areas of MAV control,robust navigation,statistical signal processing,singularly perturbed control system and hybrid control system.She is a member of IEEE and AIAA.

Abdelkarim Nemrareceived the M.E.and M.S.degrees in control systems from the Department of Control,Polytechnic Military School,Algeria,in 2004 and 2006,respectively.He received the Ph.D.degree in Control systems from the Department of Informatics and Sensors,Cranfield University,Shrivenham,UK in 2010.His current research interests include unmanned vehicles,localization of aerial vehicle and map building.His publications include a number of conference and journal papers in computer vision and data fusion and book chapter in robotics.