亚音速气流中曲壁板的分岔研究
刘少文, 李鹏, 杨翊仁
(西南交通大学力学与工程学院, 成都610031)
亚音速气流中曲壁板的分岔研究
刘少文, 李鹏, 杨翊仁
(西南交通大学力学与工程学院, 成都610031)
研究了具有初始曲率的二维曲壁板在亚音速气流中的分岔问题。考虑大变形和粘弹性的影响,通过模态展开法获得了曲壁板上的静、动态气动压力;采用Galerkin方法将振动控制方程离散为常微分方程组;采用牛顿迭代法求解方程组得到了静变形位置;在参数空间内分析了曲壁板的分岔特性;采用Runge-Kutta方法进行数值计算得到了曲壁板的时程响应相图。结果表明:曲壁板的初始变形会产生静态气动力,并会使得曲壁板产生新的静平衡点位置;当气流动压超过临界动压后,系统将会产生尖点分岔现象,使其平衡点的数目和稳定性发生变化;系统的稳定响应与气流动压及初值有关。
曲壁板;亚音速气流;静态变形;尖点分岔;时程响应
引言
随着中国高速铁路的发展和相关研究逐渐开展,许多之前在设计普速列车时合理忽略的气动力问题在高速列车中逐渐凸显出来。例如,车身蒙皮和车窗等结构在列车高速运行时的流致振动问题,其可归结为壁板结构在低亚音速气流中的气动弹性问题。
现有的壁板气动弹性问题主要集中在航空航天领域,并且是以超音速气流中的平壁板为主。Dowell E H[1]等对超音速气流中的壁板颤振问题作了综述研究,归纳总结了在理论和实验中得到的一些成果,并展望了未来的研究方向;文献[2]使用Galerkin方法研究了双侧受超音速气流的二维受热平壁板的气动弹性问题,开创性地探讨了双侧均受气动力作用的平板的气动弹性特性;Kornecki A[3]基于气流为不可压缩的理想流体推导得到气动力的近似表达式,研究了小变形下的二维平壁板的气动稳定性问题;文献[4]考虑了亚音速气流的可压缩性,采用级数展开法得到了气动力的表达式,研究了大变形二维平壁板的失稳、分岔和非线性响应等动力学问题,其为亚音速气动力的求解提供了一种值得参考的方法。对于含有初始曲率变形的曲壁板问题,现有的文献都仅针对超音速壁板。Dowell E H[5-6]研究了超音速气流作用下的二维曲壁板及三维曲壁板的非线性颤振问题;杨智春[7-8]等研究了带有初始几何曲率的二维曲壁板在超音速气流中非线性颤振特性,文中气动力均为含有曲率修正项的活塞理论,且指出由于初始曲率的存在,曲壁板将会出现与平壁板不同的气动弹性特性。对于亚音速气流中曲壁板的气动弹性问题研究,目前鲜有正式的研究公开发表。对于高速列车中的车身蒙皮和车窗等壁板结构而言,为满足流线型设计要求,其均不可避免地会带有一定的初始曲率。因此,研究低速气流中的曲壁板气动弹性问题具有一定的理论和实际意义。
本文考虑为不可压缩的理想流体,采用模态展开法得到了静、动态气动力的表达式。应用Von Karman大变形理论建立了带有初始曲率的二维曲壁板的结构振动方程。运用Galerkin法离散系统,应用牛顿迭代法求解非线性方程组,使用数值分析方法分析曲壁板的静态变形、稳定性、分岔及时程响应等动力学问题。
1 结构运动方程的建立
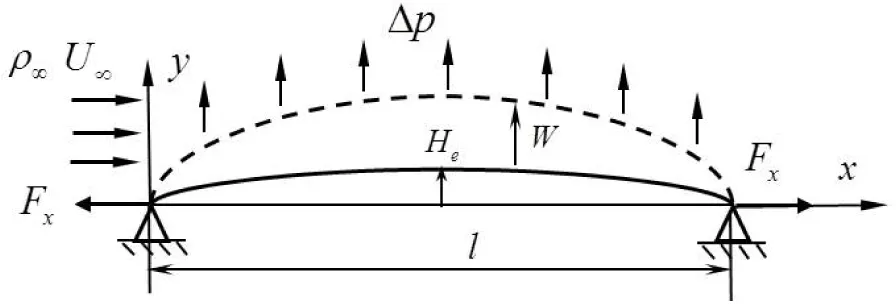
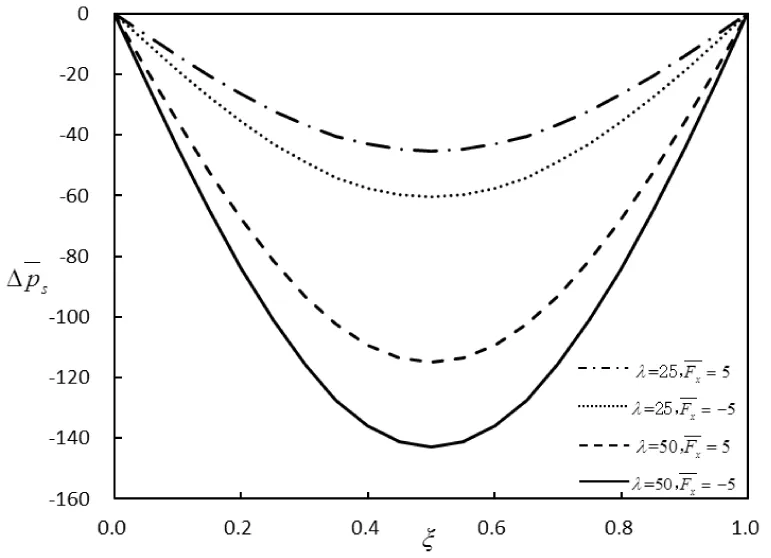
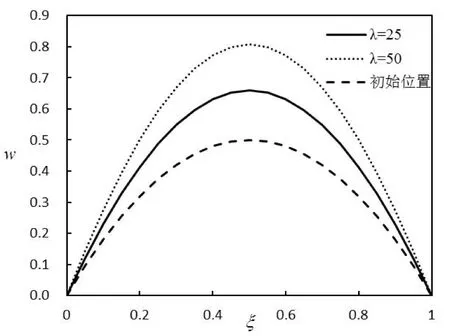
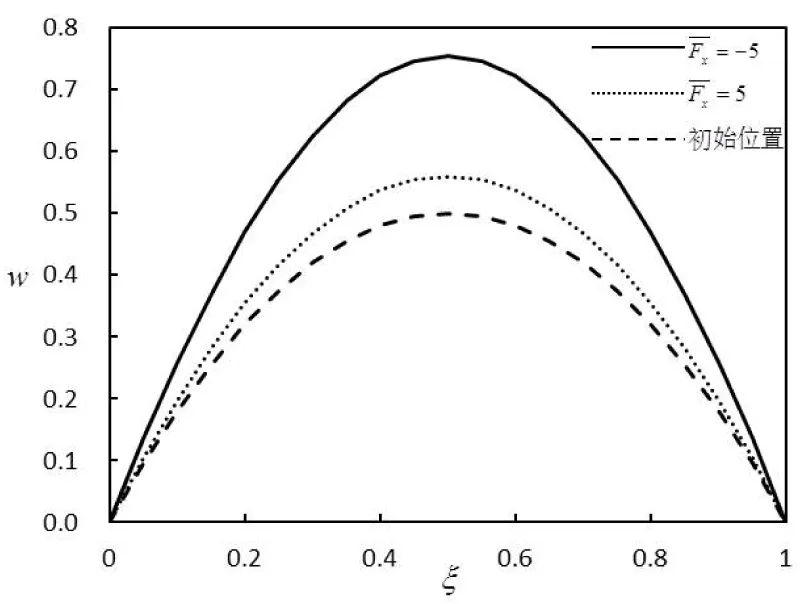
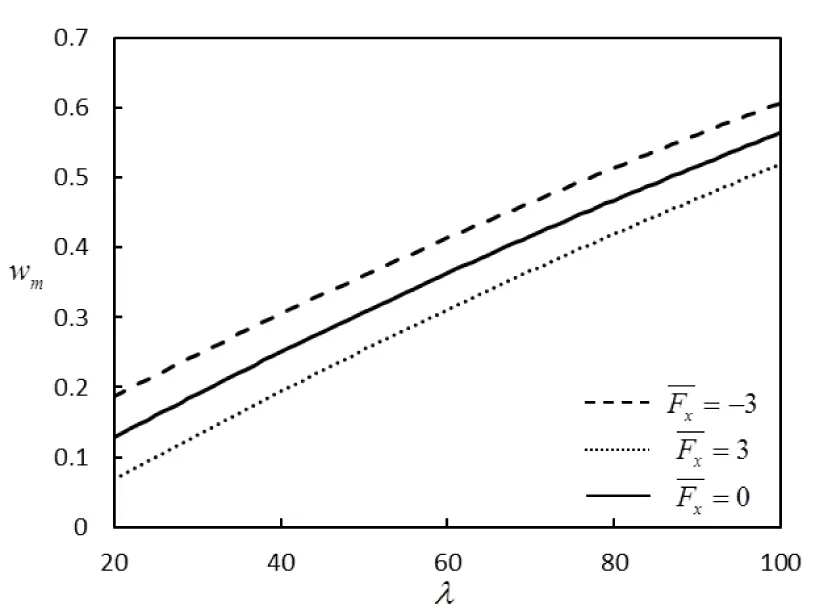
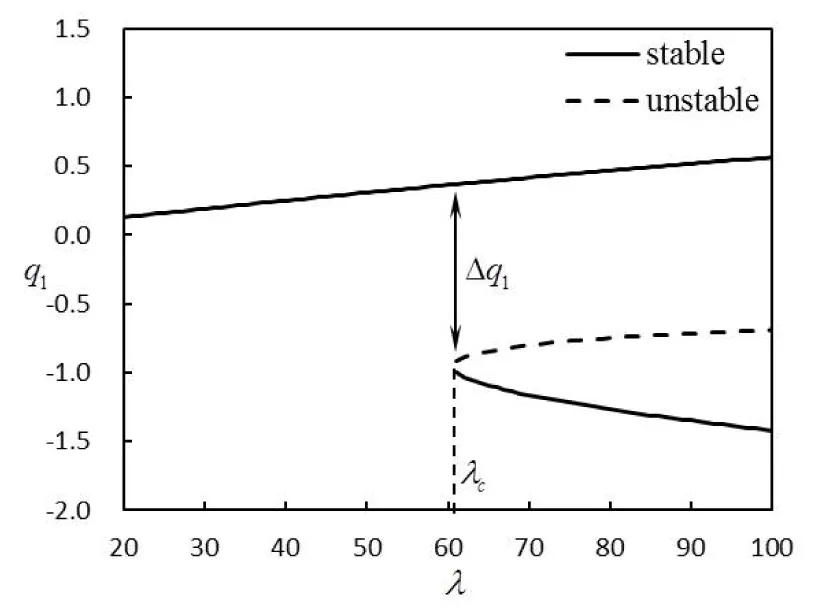
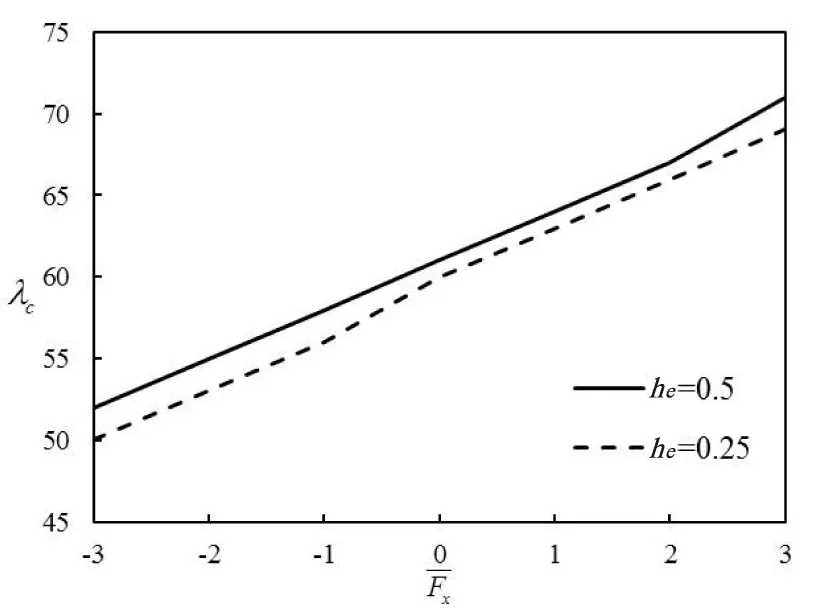
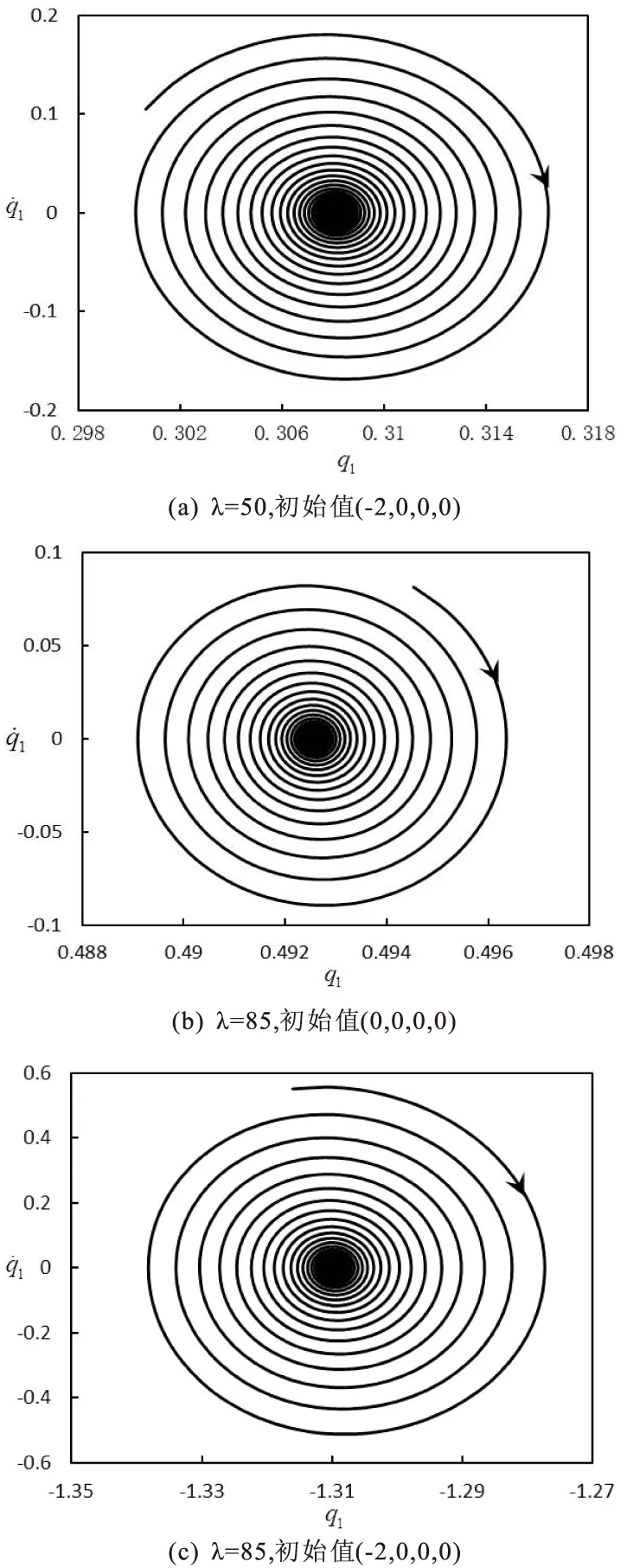
对于实际的简支曲壁板结构,若其宽度远大于长度和厚度,则可简化为如图1 所示二维曲壁板结构,其两端简支在y=0平面内。板的密度为ρ,长度为l,厚度为h,壁板中部初始位移为He,且h< 考虑Von Karman大变形非线性影响,基于Hamilton原理可得壁板运动控制方程为[5]: (1) 其中: W为壁板位移,△p为壁板上的气动压力(向下为正)。 图1 亚音速气流中的二维曲壁板示意图 本文考虑初始变形曲率为常数的圆弧,其几何表达式为[5]: (2) 气动压力△p由两部分组成:由壁板运动产生的时变动态压力△pd和由壁板初始变形产生的静态压力△ps,即,△p=△pd+△ps。当变形较大时,由Bernoulli方程可得△p为 (3) (4) 及边界条件: (5) φ=0 (y→+∞) (6) 将壁板的动位移W和初始位移W0写作: (7) 其中: 将式(7)代入到式(5)可得: (8) 根据式(8),并采用分离变量法设: (9)将式(9)代入式(4),并联立式(3)、(5)、(6)、(8)可得: (10) 其中: 引入下列无量纲参数: 式(2)对应的无量纲初始曲率为: Γx=8he (11) 将无量纲参数对应代入方程(1)、(10),利用正交性可得离散的常微分方程: (12) 其中: 研究曲壁板在气动力作用下的静平衡位置。在式(12)中取n=2,可得关于静平衡位置的方程为: (13) 其中: 使用牛顿迭代法可以求得此方程的解,进而可以得到曲壁板在气动力作用下的静平衡位置。以国内高速列车普遍使用的铝合金面板为算例,其主要参数E=69 GPa,ρ=2705 kg/m3,υ=0.3 ,l=800 mm,h=2.5 mm,取气流密度ρ∞=1.2 9 kg/m3, 曲壁板中间初始位移为He=1.2 5 mm。 图2 静变形下的静态气动力分布图 图3 和图4分别表示了曲壁板在不同动压和轴力作用下的静态变形。从图中可以看出,曲壁板将会向气流一侧产生位移;位移沿中点呈对称分布,并随着动压及轴向压力增大而增大。 图3 不同动压下的曲壁板静变形图 图4 不同轴力下的曲壁板静变形图 图5给出了壁板中部静位移wm在不同轴力作用下随动压的变化关系。由图可知,板的变形随着动压的增大而增大,并呈现非线性关系,且随着动压增大,壁板变形量的增大呈现放缓趋势。 图5 不同轴力作用下静位移随动压变化趋势图 n=2,i=1,2 (14) 其中: 图6给出了系统的平衡点数目、位置和稳定性情况随来流动压的变化情况。可以看出,系统存在一个临界动压值λc(λc≈60.7),当λ<λc时,系统存在一个稳定的平衡点;当λ>λc时,系统出现了两个稳定的平衡点和一个不稳定的平衡点,此时系统发生了尖点分岔现象。尖点分岔是一种突变现象,其是由于系统为非对称系统而产生的。与平板一般发生的叉式分岔不同[4,9],尖点分岔在分岔处将会产生跳跃现象,如图所示,该跳跃现象归结于静态气动力对系统产生的非对称性。 图6 曲壁板的尖点分岔图 图7表示曲壁板在不同初始小曲率和轴力作用下的分岔动压参数λc的变化图。从图中可以看出,λc随无量纲轴力的增大而增大,随初始变形的曲率减小而减小。 图7 不同初始变形下轴力与临界动压关系 采用变步长Runge-Kutta方法对方程(14)在不同的初始条件下进行数值求解可得系统响应,如图8所示。从图8(a)可知,当λ<λc时,系统作振幅衰减的振荡运动,直至收敛到稳定平衡点(q1+);当λ>λc时,系统将会依据初始条件收敛到某一个稳定点(q1+或q1-),如图8(b)~8(c)所示。这是由于两支稳定分支上的奇点存在各自的吸引域。对于各自稳定点的吸引域范围的分布问题研究,正是下一步需要做的工作。 图8 不同动压和初值下的相图 (1) 曲壁板的静态变形随动压及轴向压力的增大而增大,反之则会越小;壁板的变形将会随着变形量的增大呈现放缓趋势。 (2) 系统将产生尖点分岔,系统平衡点个数和稳定性将会发生变化;临界动压与曲壁板的初始曲率以及轴力有关。系统的稳定响应与初值、动压相关。 [1] DOWELL E H.Panel flutter:a review of the aeroelastic stability of plates and shells[J].AIAA Journal,1970,8(3):385-399. [2] ZHOU J,YANG Z C,GU Y S.Aeroelastic stability analysis of heated panel with aerodynamic loading on both surfaces[J].Technological Sciences,2012,55(10):2720-2726. [3] KORNECKI A,DOWELL E H,O’BRIEN J.On the aeroelastic instability of two dimensional panels in uniform incompressible flow[J].Journal of Sound and Vibration,1976,47(2):163-178. [4] LI P,YANG Y R,XU W,et al.On the aeroelastic stability and bifurcation structure of subsonic nonlinear thin panels subjected to external excitation[J].Archive of Applied,Mechanics,2012,82(9):1251-1267. [5] DOWELL E H.Nonlinear flutter of curved plates[J].AIAA Journal,1969,7(3):424-431. [6] DOWELL E H.Nonlinear flutter of curved plates II[J].AIAA Journal,1970,8(2):259-261. [7] 杨智春,周建,谷迎松.超音速气流中受热曲壁板的非线性颤振特性[J].力学学报,2012,44(1):30-38. [8] 张蕊丽,杨智春.曲壁板在超音速气流中的分岔特性[J].力学学报,2010,42(5):863-869. [9] 李鹏,杨翊仁,鲁丽.外激励作用下亚音速二维壁板分岔及响应研究[J].力学学报,2011,43(4):746-754. [10] 高普云.非线性动力学-分叉、混沌与孤立子[M].长沙:国防科技大学出版社,2005. Bifurcation Analysis of Curved Plate in Subsonic Flow LIUShaowen,LIPeng,YANGYiren (School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China) The bifurcations of two-dimensional curved plate with initial curvature in subsonic flow is studied. Considering the influence of large deflection equation and viscoelasticity. The static and dynamic aerodynamic pressure of curved plate is derived on modal superposition method. The governing partial differential equation is transformed to a series of ordinary differential equations by using Galerkin method. Solving the equations by Newton iteration method, the position of static deformation is obtained. Bifurcation of the curved plate is studied in a parameter-space, and the Runge-Kutta method is used to calculate the time history response of curved plate phase diagram. The results show that: the initial deformation of the curved plate lead to static aerodynamic force and a new static position, the system will undergoes an imperfect-like bifurcation resulting in the change of the number and the stability of equilibrium points and the steady response to the system is closely related to the dynamic pressure and initial value. curved plate; subsonic flow; static deformation; cusp bifurcation; time history response 2016-03-21 国家自然科学基金(11302183);四川省应用基础研究计划项目(2015JY0083) 刘少文(1989-),男,湖南永州人,硕士生,主要从事流固耦合动力学方面的研究,(E-mail)lp_vib@swjtu.edu.cn 1673-1549(2016)05-0057-06 10.11863/j.suse.2 016.05.1 3 TB115 A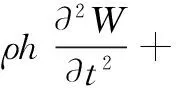
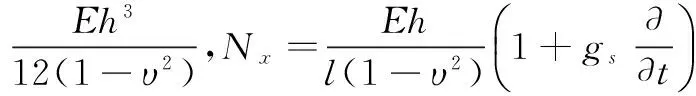
2 气动力的表达式
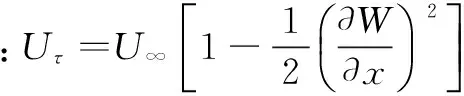
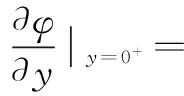
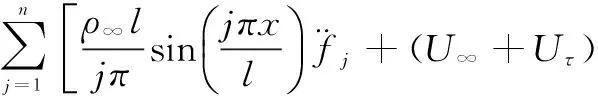
3 方程的离散
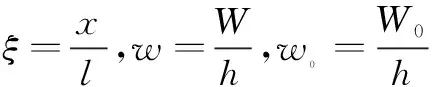
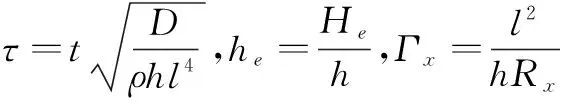
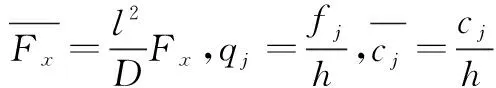
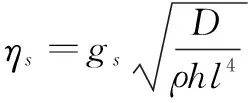
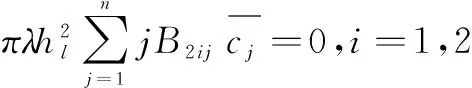
4 静平衡位置和静态气动力的计算

5 分岔及稳定性分析
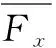
6 结论

