复合材料圆角区结构完整性研究

任飞翔， 张钦博

(成都飞机设计研究所， 成都610014)



复合材料圆角区结构完整性研究

任飞翔， 张钦博

(成都飞机设计研究所， 成都610014)

先进复合材料在飞机结构中的应用越来越广泛，且开始出现在中央翼盒段、机翼等主承力结构上。实际应用中发现，在梁圆角区或者肋根部的倒角区，复合材料极易发生分层破坏，对结构的安全性构成严重的威胁，故复合材料圆角区结构完整性的研究具有重要的意义。使用有限元软件Abaqus，采用三维Hashin复合材料损伤判据，从复合材料圆角区的破坏模式和初始损伤对结构承载能力的影响两个方面对复合材料圆角区进行了分析研究。研究结果表明，该结构型式的主要破坏模式为分层破坏，且破坏起始位置均在靠近内侧厚度的约1/4处；初始损伤的存在对结构承载能力的影响是致命的，可使结构的承载能力降低约75%～80%。

复合材料；结构完整性；圆角区；渐进损伤；失效模式；三维Hashin准则

引言

先进复合材料和金属材料相比，在比强度、比刚度、疲劳特性和破损安全等方面均表现得更加优越，为了有效地减轻结构重量，飞机结构中复合材料的用量越来越高，且应用范围从非承力构件(口盖等)逐步扩展至次承力构件(水平尾翼等)，目前已应用到中央翼盒段等主承力部件上[1-2]。

复合材料结构和传统金属结构在分析方法上不尽相同，例如对厚度方向上应力的关注程度。金属结构一般为各向同性材料，而复合材料层间性能较弱，特别是对于大曲率的复合材料构件，厚度方向上的应力变化比较剧烈，容易发生分层破坏，对结构的安全性构成严重的威胁。典型的部位有飞机机翼油箱区C型翼梁的圆角区[3]和肋根部[4]。

针对圆角区结构完整性问题，J.B.Kosmatka等人建立了两节点Shear-Deformable梁单元对受剪切载荷的曲梁进行了研究[5]；William L. Ko等人则应用经典层压板理论对圆角区的应力和位移分布进行了理论计算[6]；王秋宇等人应用经典层压板理论对梁圆角区层间应力的计算方法进行了研究[7]；ESDU软件则实现了厚度方向上的应力分布和失效分析[8]；ASTM标准D6415则对复合材料圆角区的强度试验方法进行了详细的阐述[9]；T. Edwards and J. Thompson对A400M机翼C型梁的圆角区试验进行了分析模拟，主要验证了沿厚度方向上的应力分布，且对能量释放率进行了修正[3]。

本文采用三维Hashin损伤准则，使用Abaqus商用有限元软件，对复合材料圆角区进行了分析，确定了圆角区的破坏模式和承载能力，并且对预制损伤对结构承载能力的影响进行了研究，对该区域的结构设计有一定的工程指导意义。

1 模型建立

1.1 试验件细节

试验件示意图如图1 所示，其中t为厚度；θ为两直边夹角；R为圆角外半径；w为试验件宽度；L为直边长度。各试验件具体尺寸细节见表1。复合材料为T800/BA9918纤维树脂体系。

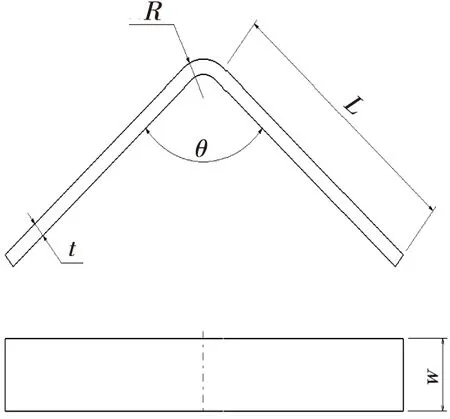
图1 试验件示意图表1 试验件几何尺寸

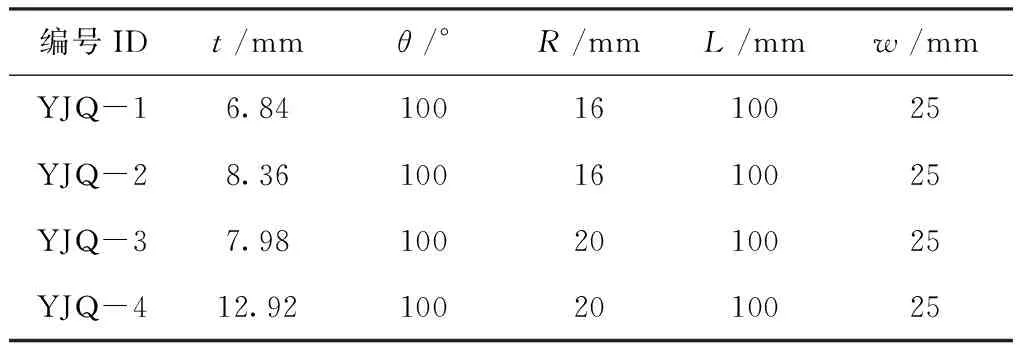
编号IDt/mmθ/°R/mmL/mmw/mmYJQ-16.841001610025YJQ-28.3 61001610025YJQ-37.981002010025YJQ-412.921002010025

制造过程中产生的分层缺陷，用12.5 mm×12.5 mm的Teflon材料或两层聚四氟乙烯薄膜模拟，如图2 示所示，编号为YJQ-D-1、YJQ-D-2…。

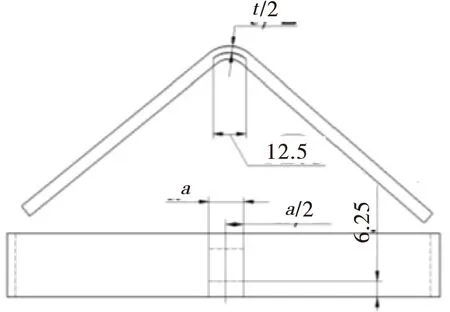
图2 分层位置示意

试验夹具设计参考ASTM-D6415标准，采用四点弯方案，如图3 所示。上半部分为加载端，提供载荷，下半部分为底座，固定在试验机平台上。

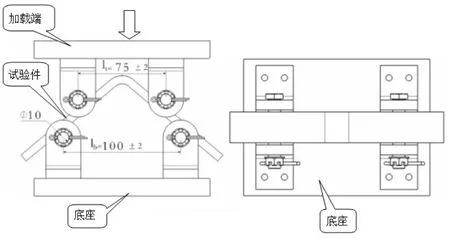
图3 试验夹具

试验件复合材料板铺层顺序见表2。

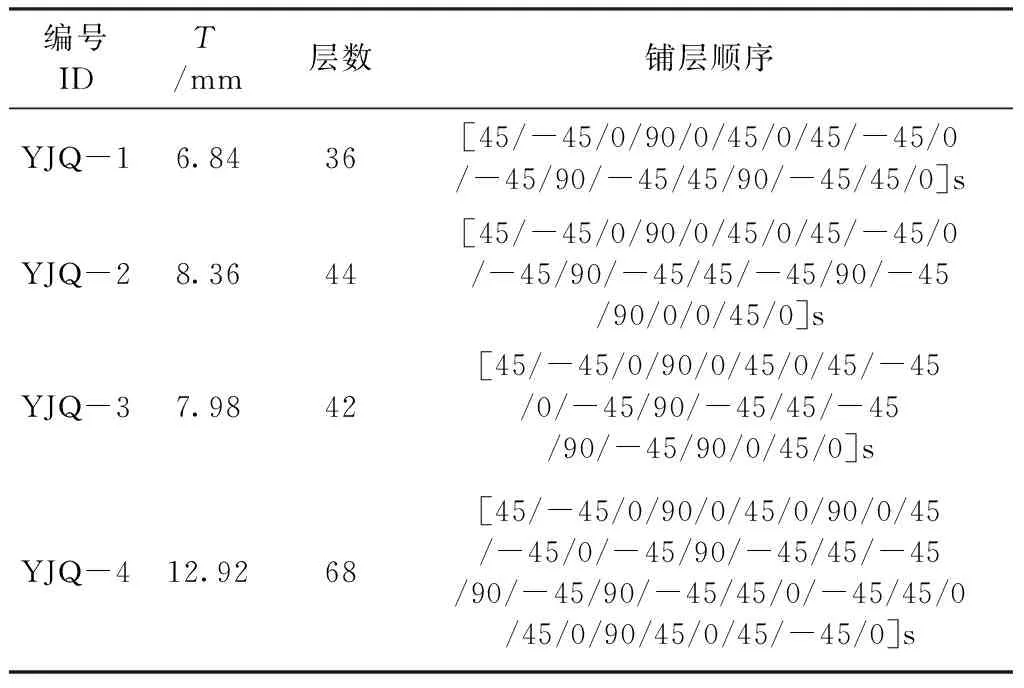
表2 试验件复合材料铺层顺序

1.2 三维Hashin损伤准则简介

Abaqus中用户可以自定义损伤准则，此处采用三维Hashin准则，为了简化分析，只考虑了层间分层损伤，损伤准则如下：

法向拉伸时，σ33>0：

法向压缩时，σ33<0：

其中，ZT为基体拉伸强度，ZC为基体压缩强度，S13、S23为层间剪切强度。

由于两种损伤模式的表现形式均为层间分层，考虑到基体的拉伸和压缩强度不同，所以分成了两个判据，下文中以拉伸分层和压缩分层以示区别。

1.3 有限元建模

考虑到结构的对称性，为了简化模型、提高计算效率，使用Abaqus建立1/2模型，如图4所示。采用C3D8R实体单元对结构进行离散，预制分层损伤用去除相应位置的Cohesive单元进行模拟。在设置材料属性时，为了消除加载和支持处应力集中的影响，直边内外表面的5层单元未设置损伤判据(如果设置损伤，由于加载和支持处有应力集中，此处的复合材料极易发生损伤，从而影响加载)，其他层采用Abaqus用户自定义材料子程序USDFLD设置材料属性。圆角区在设置属性时使用圆柱坐标系[10]。

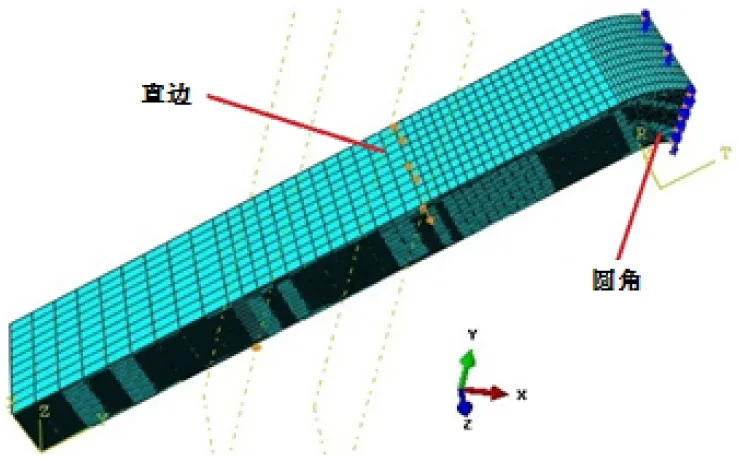
图4 有限元模型及边界条件

边界条件：由图3 可看出，在加载过程中，加载和支持处都会发生移动，边界条件的精确模拟比较困难。此处为了简化分析，认为加载过程中，加载和支持处的移动距离很小，可以认为是固定的。加载点和支持点都认为在圆柱和直边的接触点上，可由图中的参数计算出加载点和约束点的位置。在加载点施加垂直于表面的位移载荷，与此同时约束Z方向的位移；在支持点，约束垂直于表面的以及Z方向的位移；在对称面上施加对称约束，参见图4。

2 有限元结果及分析

2.1 完好试验件

根据有限元分析，完好试验件的加载历程以及最后结果是类似的，故以YJQ-1试验件为例，对结果进行讨论和分析。

试验件载荷时间历程曲线如图5所示，曲线有拐点和掉载点，分别对应着A点和B点。曲线最高点B点即代表了试验件的破坏载荷，约为5.01 kN。首先出现的损伤模式为拉伸引起的复合材料的分层，起始位置如图6所示，对应着载荷时间历程曲线中的拐点A，损伤起始出现在8～9层(从圆角内侧数)，在厚度的1/4(靠近圆角区内侧)处附近。

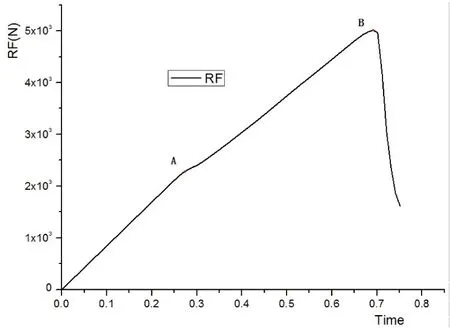
图5 YJQ-1载荷-时间历程

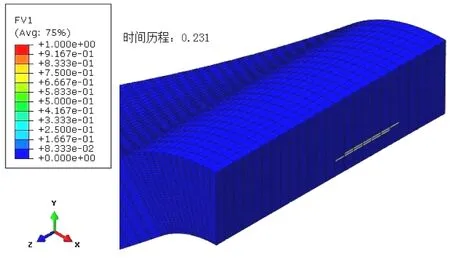
图6 YJQ-1拉伸分层损伤起始位置

如图7所示，载荷时间历程曲线掉载点，即图5中B点，对应的复合材料拉伸和压缩分层损伤的扩展情况分别对应FV1和FV2，灰色单元为损伤单元，如无特别注明，下同。可以看出，复合材料的拉伸分层损伤几乎充满了整个圆角区，而压缩分层损伤除了极少一部分出现在圆角处，大部分出现在加载点和支持点之间的复合材料上，但整体面积相对拉伸分层损伤来说比较小，所以可以认为复合材料拉伸分层损伤的扩展导致了结构承载能力的下降，并最终导致掉载。

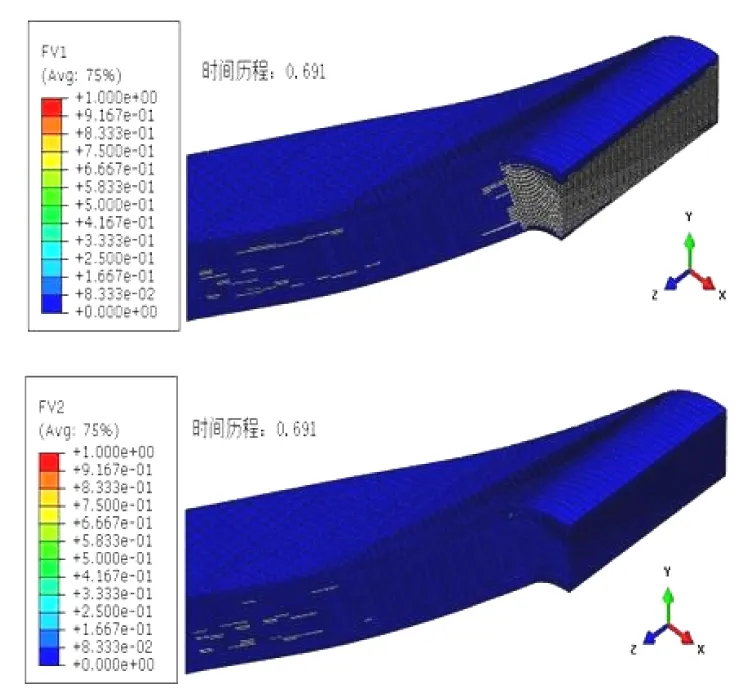
图7YJQ-1曲线掉载点复合材料损伤

根据完好试验件加载历程及结果统计(表3 )，可得出：

(1) 完好试验件载荷时间历程曲线都存在拐点和掉载点，也就曲线中的A点和B点。

(2) 试验件损伤起始位置几乎都在厚度的约1/4处(靠近圆角区内侧)。

(3) 复合材料的拉伸分层是主要的损伤模式，也是导致结构失效的主要原因。

表3 完好试验件计算结果

2.2 含缺陷试验件

根据有限元分析，含缺陷试验件的加载历程及结果也比较类似，以YJQ-D-1试验件为例，对结果进行讨论和分析。

试验件载荷时间历程曲线如图8所示，从图中可以看出曲线有很长一段的线性段，当载荷增加到一定程度时，模型的刚度开始出现折减，曲线出现掉载即图中A点，此时载荷约为1.03 kN。

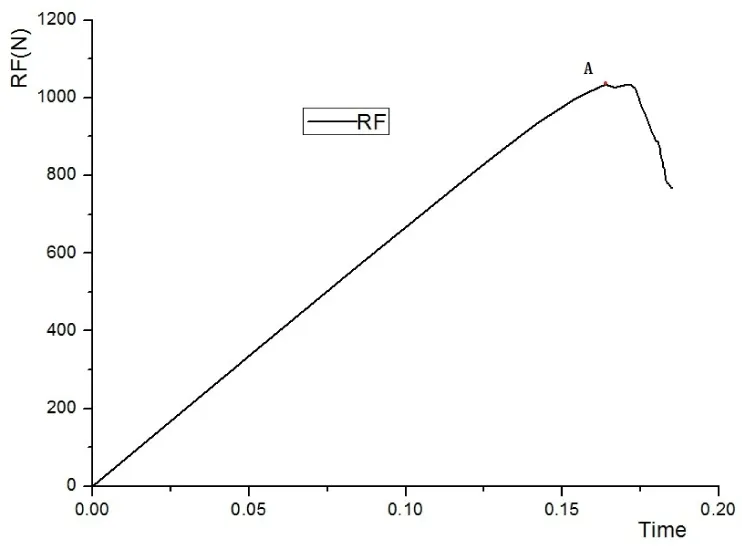
图8 JQ-D-1载荷-时间历程

试验件粘接元首先出现损伤，损伤位置和时间历程如图9所示。随后复合材料出现拉伸分层损伤，如图1 0所示。比较两图可以发现，两种损伤起始的时间历程和损伤起始位置都很接近，可以认为两种损伤模式同时起始，且起始于同一位置，这也符合预期。

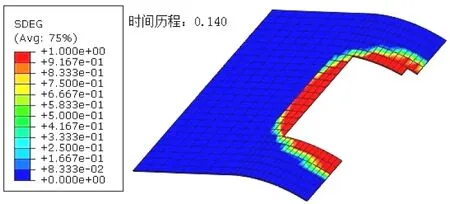
图9 YJQ-D-1Cohesive单元损伤起始

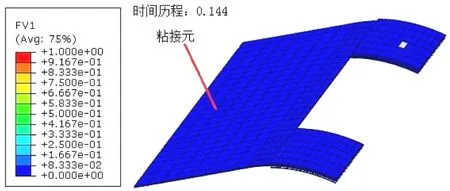
图10 YJQ-D-1复合材料拉伸分层损伤起始

载荷时间历程曲线掉载点，即图8中点A，对应的复合材料拉伸分层损伤以及粘接元损伤的扩展情况如图11所示。可以看出，在预制分层的周围，复合材料拉伸分层损伤面积已经相当可观，且左侧面积略大于右侧，说明损伤向圆角内侧扩展多于向外侧的扩展。反观粘接元的损伤情况，损伤面积的扩展不是很大，左侧的损伤面积略微大于右侧。

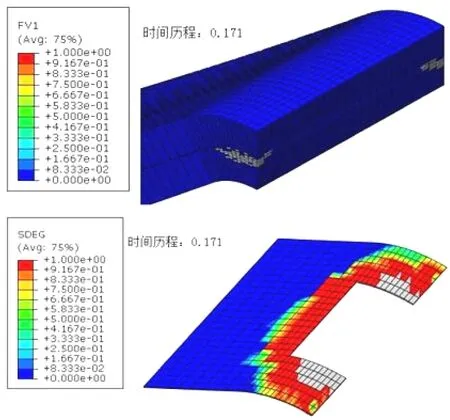
图11 YJQ-D-1载荷曲线掉载点损伤情况

结合含损伤试验件加载历程及结果，可以得知：

(1) 载荷时间历程曲线开始均为线性段，然后刚度出现折减，接着出现掉载。

(2) 复合材料的拉伸分层和粘接元损伤，两种损伤模式起始的时间几乎相同，且起始于同一位置。

(3) 当载荷曲线出现掉载时，两种损伤模式向左侧扩展多于右侧，且圆角内侧的损伤要多于圆角外侧。

(4) 当达到破坏载荷时，复合材料拉伸分层损伤面积均明显大于粘接元的损伤面积。

2.3 完好和含损伤试验件对比

首先比较两类模型的最终破坏载荷。完好试验件和含损伤试验件最终破坏载荷见表4。由表4 可知，初始分层缺陷对圆角区的性能有较大的影响，预制分层使得结构的承载能力降低了75%～80%。

其次是损伤模式和损伤位置。完好试验件的损伤模式出现的先后顺序相同，都是拉伸分层损伤出现较早，损伤起始位置都在靠近圆角内侧、厚度的1/4处附近，然后向圆角内外两侧扩展。当试验件出现掉载时，整个圆角区几乎充满了拉伸分层损伤，且内侧多于外侧。压缩分层损伤起始较晚，扩展也较小，只是出现在圆角区和直边的结合处，以及在加载点和支持点之间；含缺陷试验件损伤模式出现的先后顺序也相同，均是复合材料拉伸分层损伤和粘接元损伤(LYWQ-2除外)，几乎是同时发生的。损伤起始的位置各个模型各异，但是基本都位于预制分层损伤周围，之后损伤向周围扩展。当试验件出现掉载时，复合材料拉伸分层损伤面积左侧大于右侧，圆角内侧的损伤要多于圆角外侧，这点基本是相同的。粘接元损伤也是向左侧扩展比较严重，和复合材料拉伸分层保持一致。

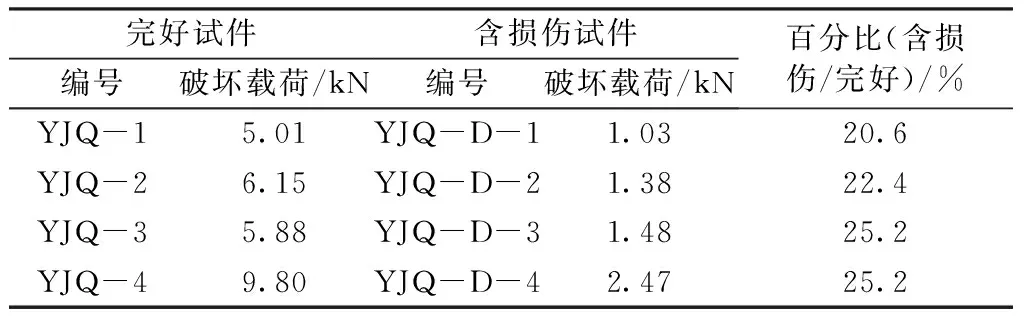
表4 完好和含损伤试验件承载能力对比

3 结论

文章使用Abaqus有限元软件建立了完好和含损伤的试验件共8个有限元模型，采用自定义子程序USDFLD定义了材料属性，复合材料损伤判据选择三维Hashin损伤准则，对复合材料圆角区进行了分析。完好试验件主要考察的是复合材料层间分层损伤，包括拉伸和压缩引起的分层，含损伤试验件除了上述两种损伤模式之外，还考虑了粘接元损伤。

针对上述试验件和预制损伤位置和尺寸，通过有限元模型的分析，得到了结构的承载历程以及承载能力。分析发现：

(1) 完好试验件损伤起始于厚度的约1/4处(靠近圆角区内侧)。

(2) 复合材料的拉伸分层导致完好试验件最终的破坏。

(3) 初始损伤的存在使得结构的承载能力降低了75%～80%。

[1] 中国航空研究院.复合材料结构设计手册[M].北京:航空工业出版社,2001.

[2] ROUCHON J.Fatigue and damage tolerance evaluation of structures: the composite materials response[R].NL:22nd Plantema Memorial Lecture,2009.

[3] EDWARDS T,THOMPSON J.Spar coner radius integrity for the A400M wing[J].Applied Mechanics and Materials,2005,3-4:197-204.

[5] KOSMATKA J,FRIEDMAN Z.An accurate two-node shear-deformable curved beam element[C]//Proceeding of 39th Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics,and Materials Conference and Exhibit,Long Beach,CA,US, April 20-23,1998:157-160.

[6] KO W L,JACKSON R H.Multilayer theory for delamination analysis of a composite curved bar subjected to end forces and end moments[G]//MARSHALL L H.Composite Structures 5.NL:Springer Netherlands,1989.

[7] 王秋宇,陈普会,王爱军.复合材料梁圆角区层间应力计算分析方法[J].江苏航空,2014(1):18-20.

[8] ESDUpac A9419.Through-the-Thickness Stresses and Failure in the Corner Radius of a Laminated Composite Section[R].UK:The Royal Aeronautical Society,2009.

[9] ASTM-D6415-D6415M-06ae1.Standard test method for measuring the curved beam strength of a fiber-reinforced polymer-matrix composite[S].

[10] 袁菲.复合材料翼梁圆角过渡区弯曲试验的仿真分析[D].南京:南京航空航天大学,2012.

Analysis of Structural Integrity for Corner Radius of Composite

RENFeixiang,ZHANGQinbo

(AVIC Chengdu Aircraft Design & Research Institute, Chengdu 610014, China)

Advanced composite has been widely used in aircraft structure, and even can be seen in primary load-bearing structure such as airplane wing spar and wing box. During the employment of laminated carbon fiber reinforced plastic composite structure, through-thickness(inter-lamina) failure is incidental in the corner radius of ‘C’-section spar and rib foot, which is of high risk for structural integrity. So the study of structural integrity for corner radius has great significance. Focusing on the failure mode of corner radius in conjunction with the impact of initial damage to load capacity using finite element software Abaqus and applying 3D Hashin damage criteria, it is concluded that delamination is the primary failure mode, damage initiates from the 1/4 thickness (hereabout the inner surface), the existence of initial lacuna is fatal to structural load capacity, declining about 75%～80%.

composite; structural integrity; corner radius; progressive damage; failure mode; 3D Hashin damage criteria

2016-03-30

任飞翔(1989-)，男，四川成都人，工程师，硕士，主要从事复合材料结构设计与分析方面的研究，(E-mail)rentianyu1989@163.com

1673-1549(2016)05-0047-05

10.11863/j.suse.2 016.05.11

TB115

A