考虑连接界面局部非线性的动力学分析方法

王东， 胡杰， 万强

(中国工程物理研究院总体工程研究所， 四川绵阳621999)



考虑连接界面局部非线性的动力学分析方法

王东， 胡杰， 万强

(中国工程物理研究院总体工程研究所， 四川绵阳621999)

连接界面上存在的多尺度、多物理场等复杂行为是引起结构阻尼和刚度非线性的主要原因。针对连接界面上典型的刚度软化、迟滞非线性行为，采用Iwan模型模拟连接结构进行力学建模，并推导了含有非线性连接的动力学微分方程。然后，采用时频交替方法求解非线性动力学方程在周期性激励作用下的稳态响应，并与数值积分方法计算的响应进行对比，最后研究了不同激励频率对连接界面非线性特性的影响。结果表明：Iwan模型能够较好地描述连接界面的刚度软化、迟滞特性，时频交替方法能够更加快速精确地求解非线性系统的稳态响应，随着激励频率的增加，位移响应最大值减小，迟滞曲线面积也相应减小。

连接界面；局部非线性；Iwan模型；时频交替；迟滞

引言

连接界面不仅是引起结构能量耗散和阻尼衰减的主要原因，还会造成结构刚度的下降[1]。连接界面上力学参数的测量和非线性行为表征方法一直是连接结构力学研究的瓶颈，也是制约着复杂结构动力学分析、高保真预测仿真、设计、优化和控制等问题的关键所在[1-2]。同时，由于连接界面力学行为的复杂性以及对连接界面进行直接实验观测的困难，连接界面的力学建模也是非常具有挑战性的科学问题。

连接界面行为的复杂性将导致连接结构动力学行为也异常复杂，出现诸如接触碰撞导致的能量在低频和高频之间的传递、结构出现超谐波响应，或者由切向黏滑行为导致的界面能量耗散、微动磨损等现象[3-4]。研究者们通过试验和理论研究发现接触面存在激励力-位移非线性软化刚度、迟滞特性等典型的非线性行为[5-7]。Chen等人通过二维直板模型的精细有限元仿真，得出了位移和激励力的非线性软化刚度特性，并且得出整个接触面上相对位移随着切向激励幅值变化的规律，说明了接触面上微观滑移发生的过程[5]。Gaul等人通过试验验证了激励力-位移的非线性软化刚度特征，发现随着切向载荷增大，界面逐步从微观滑移进入部分滑移状态[6]。Sandia针对螺栓连接结构进行了深入的研究，发现了连接界面的非线性刚度软化和迟滞特性[7]。

随着接触力学、摩擦学和塑性力学等学科的发展，人们开始从不同的角度来考虑连接问题，建立了多种描述连接界面非线性行为的模型[8-10]。比较经典的模型主要有考虑黏滑特性的Iwan弹簧滑块[11-12]、Lugre毛刷模型[13]、 Valanis模型[13]等。相比于Lugre毛刷模型和Valanis模型，Iwan模型更为系统和完善地描述了界面的微观“黏滑”过程，而且模型和参数具有一定的物理意义，因此，Iwan模型逐渐被认为是较为合适反映连接界面机理的“唯象”模型。Segalman利用Iwan模型提出了一种描述连接界面黏滑行为的四参数模型[14]。Song等人对Iwan串并联模型进行了修正，提出一种Iwan连接梁单元，这种单元可以直接应用到连接梁结构的有限元仿真程序中[15-16]。

本文采用Iwan模型模拟连接结合面上的典型非线性行为，建立了系统微分动力学方程，基于时频交替法求解出系统在谐波激励下的稳态解，并同数值积分解进行了对比，且研究了不同激励频率对连接界面非线性行为的影响。

1 连接界面的等效建模

为了获得栓接结合部刚度软化的非线性特征，设计如图1 (a)所示的搭接连接系统模型，模型中下连接件固定，上连接件考虑为一维运动的刚体。x、q分别为结合面的相对位移、对应的临界滑移力，连接界面的柔性采用Iwan模型进行描述，如图1 (b)所示。

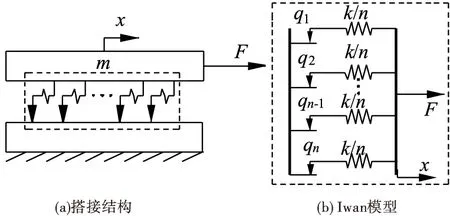
图1 搭接结构和Iwan模型

Iwan模型采用n→∞个Jenkins单元并联组成的子系统描述结合面多尺度黏滑摩擦行为。考虑螺栓结构在发生宏观滑移后仍具有一定的刚度，所以再并联一个刚度kα=αk的线性弹簧单元描述发生宏观滑动后的剩余刚度，如图2 (a)所示。子系统中每个线性弹簧的刚度都为ki=k/n，但每个滑块的临界滑移力qi并不相同。当系统切向受载时，临界滑移力小的滑块先发生滑动，随着相对位移增大，越来越多的滑块发生滑移，直至全部滑块都发生滑移，即结合界面出现了宏观滑动。因此，该模型能够复现连接界面上跨尺度黏滑摩擦过程。

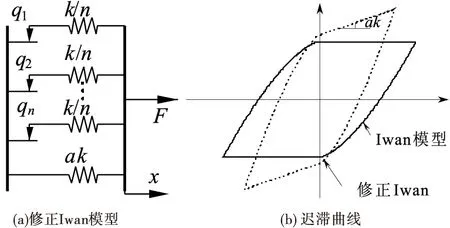
图2 修正Iwan模型与迟滞曲线

假设Iwan模型上滑块临界滑移力的分布密度函数形式为[16]：

(1)

式中，fq为系统发生宏观滑动时对应的临界宏观滑移力。对处于初始平衡位置的Iwan模型受到单调载荷的情况，其恢复力的一般表达式为：

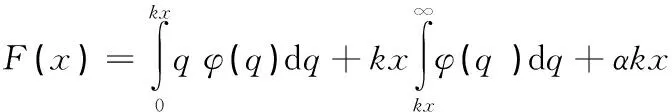
(2)

将式(1)代入式(2)中，可得：

(3)

式中分段函数包括两部分，分别表示Iwan连接模型发生微观滑移和宏观滑移时的相对位移-恢复力关系。显然，式(3)中包含一部分线性恢复力，其余为非线性恢复力。

振动载荷下，系统将会出现反复的卸载-加载运动。根据迟滞回线的对称性[17]，如图2 (b)所示，加载和卸载过程中的恢复力函数满足：

(4)

式中，Fl(x)和Fu(x)分别表示加载和卸载过程中的恢复力，x0、F0表示系统一个振动周期内的最大相对位移和恢复力。

Iwan迟滞模型描述的恢复力-相对位移关系主要受模型参数k、α和fq的影响。连接结构确定后，可按黏着条件给定未发生滑动时的等效连接刚度k，而α和fq需要通过参数辨识的方法获得。当fq=0时，连接结构将退化为线性结构，恢复力可以表示为：

F(x)=αkx

(5)

2 非线性振动分析方法

含局部非线性的结构动力学方程可以表示为：

(6)

其中，m、c、k分别为质量、阻尼、刚度矩阵，x为响应向量，fn为非线性恢复力，f为激励力。

对于周期性的激励力f，根据多谐波平衡法原理，稳定状态的响应可以表示为[18]：

(7)

对应的非线性恢复力和激励力可以表示为：

(8)

那么，式(6)对应的动力学方程满足：

(9)

即，

(10)

获得位移响应之后，速度响应和加速度响应可以表示为：

(11)

假设激励频率为fe，那么时频交替变换的间隔满足：

ω=n×2πfe

(12)

式中，n为响应一个周期内的离散数目。

根据以上推导过程，本文非线性动力学求解步骤为：

(1) 忽略非线性恢复力，即不考虑式(6)的fc，计算系统的位移响应，再根据式(11)计算速度响应。

(2) 利用步骤(1)获得的位移、速度响应计算非线性恢复力，再转换到频域的恢复力。

(3) 将频域恢复力带入到式(9)，获得频域位移和速度的频域响应，再转换到时域位移x(t)和速度。

(4) 重复步骤(2)～(3)，获得x′(t)。

(5) 对比步骤(3)和步骤(4)获得的响应，计算两次位移或速度响应的相对误差：

(13)

(6) 当迭代误差Δ小于0.01时，停止计算，输出位移、速度以及恢复力响应结果。

3 搭接结构动力学方程

典型搭接结构在法向预紧载荷P和切向周期性载荷联合作用下，连接界面上将出现黏着和滑移区域[5]，如图3 (a)所示。采用修正Iwan 模型描述结合面的黏滑摩擦行为，并考虑到结构的对称性，将搭接结构简化为图3 (b)所示的结构。

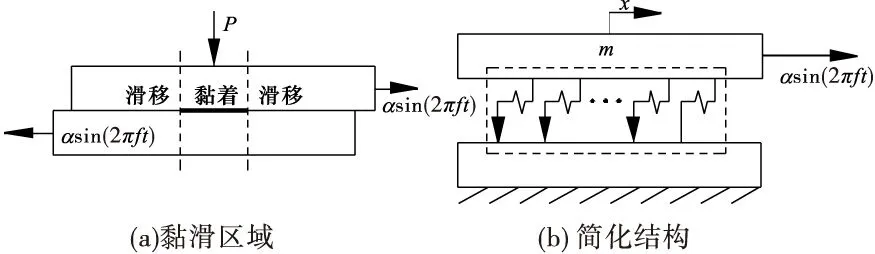
图3 搭接连接系统

将式(3)带入到式(6)中，搭接系统在受到周期性激励作用的动力学方程可以表示为：

(14)其中，ε为线性恢复力和非线性恢复力权系数，ε∈[0,1]，fu/l表示循环加载过程中非线性恢复力，a为激励力幅值，f为激励力频率。

4 结果与分析

对式(14)运动学方程进行正则化处理，两边同时乘以(k/mfq)，可得

(15)

其中，ω=(k/m)1/2，2ξω=c/m。

令y=kx/fq，式(3)正则化的非线性恢复力为：

(16)

将式(16)代入到式(15)，可得：

(17)

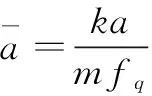
(18)

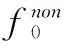
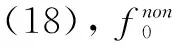
(19)

4.1 时频交替方法验证

仿真参数取作：{ω=1，ξ=0.01，ε=0.2 5，ā=20，f=0.5 }。计算搭接结构在周期性激励作用下的稳态响应，并与数值计算方法(龙格库塔四次积分)进行对比，结果如图4所示。

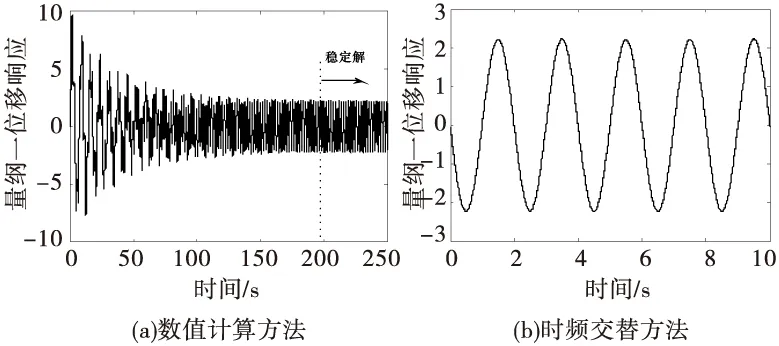
图4 响应求解效率对比结果

由图4可知，

采用数值积分方法求解稳态响应需要

计算到200 s左右，而时频交替方法只需要计算10 s就可以得到稳态响应，计算效率大大提高。为了验证时频交替方法求解非线性动力学响应的精度，截取两种方法最后三个周期内的响应进行对比，结果如图5所示。

由图5可知，本文提出的动力学响应求解方法计算得到的位移、速度、迟滞曲线与数值计算结果吻合得都很好，几乎相同，验证了本文非线性动力学求解方法有效性。由图5中位移-恢复力结果可知，随着相对位移的增加，恢复力的斜率逐渐减小，表现为连接结构的刚度软化。

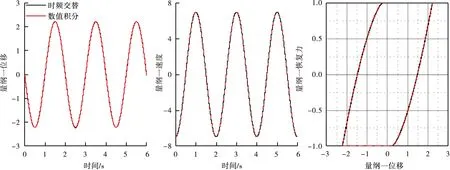
图5 搭接结构响应求解精度对比结果

4.2 激励频率对连接非线性行为的影响

由图6可知，随着激励频率的增加，最大响应的位移逐渐减小，对应的迟滞曲线面积也逐渐减少，表现为单位周期的能量耗散逐渐减少。

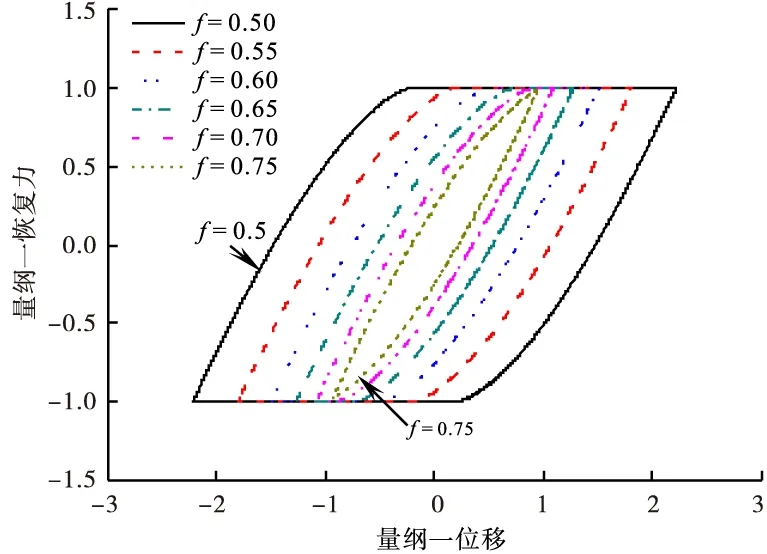
图6 不同激励频率的迟滞曲线

5 结论

本文利用修正Iwan模型模拟连接界面，推导出了搭接结构微分动力学方程，采用时频交替方法求解含连接局部非线性的动力学响应，并将本文计算的结果与数值结果进行对比，且研究激励频率对非线性行为的影响。

(1) Iwan模型能够较好地描述连接界面的刚度软化、迟滞特性。

(2) 本文提出的时频交替方法能够更加快速精确地求解非线性动力学响应。

(3) 随着激励频率增加，位移响应的最大值减小，单位周期能量耗散降低。

[1] 蔡力钢,王锋,李玲,等.栓接结合部动态特性研究进展[J].机械工程学报,2013,49(9):158-168.

[2] 马双超,臧朝平,兰海波.某航空发动机机匣的动力学模型修正[J].航空动力学报,2013,28(4):878-884.

[3] AHMADIAN H,MOTTERSHEAD J E,JAMES S,et al.Modelling and updating of large surface-to-surface joints in the AWE-MACE structure[J].Mechanical Systems and Signal Processing,2006,20(4):868-880.

[4] SEGALMAN D J,GREGORY D L,STARR M J,et al.Handbook on dynamics of jointed structures[R].Albuquerque,NM:Sandia National Laboratories,2009.

[5] CHEN W,DENG X.Structural damping caused by micro-slip along frictional interfaces[J].International Journal of Mechanical Sciences,2005,47(8):1191-1211.

[6] GAUL L,LENZ J.Nonlinear dynamics of structures assembled by bolted joints[J].Acta Mechanica,1997,125(1-4):169-181.

[7] SEGALMAN D J.Modelling joint friction in structural dynamics[J].Structural control and health monitoring,2006,13(1):430-453.

[8] 徐超,王东.考虑粗糙表面接触的连接面粘滑摩擦建模[J].西安交通大学学报,2014,48(7):131-135.

[9] 王东,徐超.一种考虑粗糙结合面切向黏滑摩擦模型[J].机械工程学报,2014,50(13):129-134.

[10] 李玲,蔡安江,阮晓光.栓接结合部迟滞非线性等效线性化方法[J].振动工程学报,2015,28(4):560-566.

[11] IWAN W D.A distributed-element model for hysteresis and its steady-state dynamic response[J].Journal of Applied Mechanics,1966,33(4):893-900.

[12] IWAN W D.On a class of models for the yielding behavior of continuous and composite systems[J].Journal of Applied Mechanics,1967,34(3):612-617.

[13] GAUL L,NITSCHE R.The role of friction in mechanical joints[J].Applied Mechanics Reviews,2001,54(2):93-106.

[14] SEGALMAN D J.A four-parameter Iwan model for lap-type joints[J].Journal of applied mechanics,2005,72(5):752-760.

[15] SONG Y X.Modeling, identification and simulation of dynamics of structures with joints and interfaces[D].Illinois:University of Illinois at Urbana-Champaign,2004.

[16] SONG Y X,HARTWIGSEN C,MCFARLAND D,et al.Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements[J].Journal of Sound and Vibration,2004,273(1):249-276.

[17] SMALLWOOD D O,GREGORY D L,COLEMAN R G.Damping investigations of a simplified frictional shear joint[R].Albuquerque,NM:Sandia National Laboratories,2000.

[18] ZUCCA S,FIRRONE C M.Nonlinear dynamic of mechanical systems with friction contacts:coupled static and dynamic Multi-Harmonic Balance Method and multiple solutions[J].Journal of Sound and Vibration,2014,333(3):916-926.

Dynamic Analysis for Local Nonlinearity of Joint Interface

WANGDong,HUJie,WANQiang

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999,China)

The complex behavior of multi-scale, multi-physics behaviors on the interface is the main reason of the structure damping and stiffness nonlinearity, Aiming at the typical stiffness softening and hysteretic behavior of the connection interface, Iwan model is applied to characterize the nonlinear softening stiffness and hysteresis behaviors of joint interfaces. With the consideration of these typical nonlinear behaviors, the dynamic differential equation of joint interface is established. Then, the alternative time-frequency method is used to analyze the steady dynamic response of system equation under the cycle oscillating force. The proposed method is investigated by the comparison with numerical integration solution. The results show that Iwan model can better describe the nonlinear behavior of softening stiffness and hysteresis between force-displacement of joint interface, and the alternative time-frequency method can solve the nonlinear dynamic equation more efficient and agree well with the numerical solution. With increase of oscillating frequency, the maximum of displacement will become less, which will induce less area of hysteresis curve.

joint interface; local nonlinearity; Iwan model; alternative time-frequency; hysteresis

2016-03-31

中国工程物理研究院科学技术发展重点基金(2014A0203006);中国工程特理研究创新发展基金(15cxj20)

王 东(1988-)，男，四川自贡人，硕士，主要从事连接界面非线性力学建模、非线性振动方面的研究，(E-mail)king_east@sina.com

1673-1549(2016)05-0052-05

10.11863/j.suse.2 016.05.1 2

TP271

A