高中函数教学中的 “文字游戏”

文/广东两阳中学　张　均

高中函数教学中的 “文字游戏”

文/广东两阳中学张均

我们高中函数有不少表面上相似但意思上不同的题型，若教师对一些易混淆的问题不阐述清楚，学生在练习或者考试的时候就会犯错，带来一些负面影响。因此教师在讲解这类题目的时候除了要让学生能够听得懂，还要让学生能够举一反三，这就需要我们从本质上理解题目的意思。本文主要探讨两类题目的教学思路与教学方法。

题型一：“对于一切x∈D，不等式恒成立”与 “存在x∈D，使得不等式成立”，其中D为该题目x的取值范围。

例1：已知不等式x2-ax+4＞0，求：

（1）对于一切x∈［1，6］，不等式恒成立，求a的取值范围；

（2）存在x∈ ［1，6］，使得不等式成立，求a的取值范围。

分析：首先我们要先教会学生分离参数，这两问都是求a的取值范围，通过化简把a移到一边得到：为了使同学们深入理解，便于对这两问进行区别，我们不妨先引入生活中的一个例子：高一 （1）班全体学生身高的范围在 165—180之间 （单位是厘米，包括165和180），班外有一位甲同学，有以下两种情况，分别求出甲同学身高的范围：①高一（1）班的所有同学的身高都要比甲同学高；②高一 （1）班里存在有学生比甲同学高。对于①，我们只要保证高一 （1）班身高最低的那个同学比甲高就满足题意了，可以推导出甲身高的范围是小于165厘米；对于②，甲同学的身高可以是小于165，也是可以是 165，166，167…甚至是179都可以 （因为在这些范围内，高一 （1）班都存在有学生高于甲，比如若甲是179，那么高一 （1）班存在有180的同学比甲要高，那么甲179的身高是满足题目意思的），推导出甲的身高的范围是小于180厘米。这个例子两问最大的区别就在于 “任意”和“存在”的区别，同时也是 “求最大值”还是 “求最小值”的区别。

题型二：“不等式的解集为D”与“不等式在D内恒成立”，其中D为一个确定的范围。

例2：已知关于x的不等式x2-ax+3＜0，求：

（1）若不等式的解集为 ｛x| 1＜x＜3｝，求a的值；

（2）若不等式在｛x|1＜x＜3｝内恒成立，求a的范围。

分析：不妨设f（x）=x2-ax+3，该函数图像开口向上，画出它的一个简图 （参见第二问示意图）。

由于不清楚对称轴的位置，在本图中可以省略掉Y轴，其中x1，x2，为方程f（x）=0的两个解，由函数图像可知，f（x）＜0，即x2-ax+3＜0的解集为 ｛x|x1＜x＜x2｝，根据题目给出的条件：不等式的解集为 ｛x| 1＜x＜3｝，推出 ｛x|x1＜x＜x2｝=｛x|1＜x＜3｝，那么x1=1，x2=3，1和3分别为方程x2-ax+3=0的两个解，由韦达定理可求1+3=a=4。

第二问，有 ｛x|1＜x＜3｝⊆ ｛x| x1＜x＜x2｝，即x1≤1＜x＜3≤x2｝，如图所示：

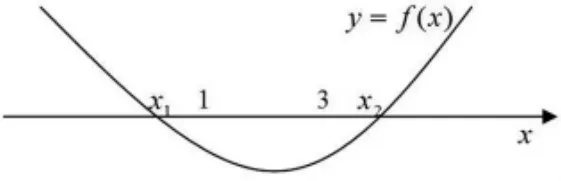
那么本问就转化为一元二次方程根的分布问题，即x2-ax+3=0的两根一个小于1，一个大于3，利用数形结合，可得到

虽然数学侧重的是思维，但是如果脱离了文字，就不能完全地理解题目本身的意思，近年高考出题喜欢在文字上做文章，对于以上两类题型，教学前一定要详细讲解问与问之间的区别，然后要想办法理解透切题目的意思，把题意转化为我们熟识的题型，必要时候可以通过一些生活中的案例和数形结合等方法来讲解，这样不但学生课堂上能够听得明白，还可以让他们做到举一反三，从而达到良好的教学效果。

责任编辑邹韵文