实测高光谱和HSI影像的区域土壤含水量遥感监测研究①

李 相，丁建丽*，黄 帅，陈文倩，王 娇，袁 泽，陈 芸

（1 新疆大学资源与环境科学学院，乌鲁木齐 830046；2 新疆大学绿洲生态教育部重点实验室，乌鲁木齐 830046；3 澳大利亚联邦科学与工业研究组织水土资源研究所，堪培拉 VIC 3169）

实测高光谱和HSI影像的区域土壤含水量遥感监测研究①

李 相1，2，丁建丽1，2*，黄 帅1，2，陈文倩1，2，王 娇1，2，袁 泽1，2，陈 芸3

（1 新疆大学资源与环境科学学院，乌鲁木齐 830046；2 新疆大学绿洲生态教育部重点实验室，乌鲁木齐 830046；3 澳大利亚联邦科学与工业研究组织水土资源研究所，堪培拉 VIC 3169）

基于典型研究区植被冠层实测高光谱数据和HSI高光谱影像数据，通过相关分析选择与不同深度土壤含水量响应敏感波段，建立两者的土壤含水量反演模型，并用实测高光谱土壤含水量反演模型校正HSI影像土壤含水量反演的模型。结果表明：土壤含水量响应敏感波段区域为450 ～ 650 nm和850 ～ 920 nm；两种土壤含水量反演模型对土壤深度为0 ～ 10 cm的土壤含水量估算效果最好，其中实测冠层高光谱土壤含水量反演模型精度高于HSI影像土壤含水量反演模型，判定系数（R2）分别为0.659和0.557；经过校正的HSI影像土壤含水量反演模型精度有了较大的提高，判定系数（R2）从0.557 提升到0.719，均方根误差（RMSE）为0.043 5，较好地提高了区域尺度条件下土壤含水量监测精度，因此运用该方法进行土壤含水量遥感监测是可行的，为进一步提高区域尺度下土壤含水量定量遥感监测提供参考借鉴。

高光谱；土壤含水量；HSI影像；多元线性回归

土壤含水量是植物生长发育的重要因子之一，是监测土壤退化程度的关键指标，在气候、生态、农业等研究领域被作为主要参数之一，特别是在干旱、半干旱区域，土壤含水量对该区域的生态健康发展起着至关重要的作用［1-2］。同时，作为陆地地表参数化的一个关键变量，在陆地与大气的物质和能量交换中也起着极为重要的作用［3］，尤其是土壤表层含水量，对于微观气象的响应更加敏感，是一个重要的能量平衡参数［4］，也是旱情监测的重要指标。

传统的重力法、张力计等方法虽然可以准确地获取某点一定深度的土壤含水量，但由于费时费力，因此难以及时、快速、准确地获取大面积的土壤含水量数据。遥感具有观测范围大、分辨率高等特点，可以实时高效地获取大范围的土壤含水量信息。随着定量遥感技术的发展，尤其是高光谱遥感技术的不断成熟和应用，使得物质组分之间的细微差异能够被更加精细地表征出来，因此成为了一种实时高效地估算土壤含水量的新手段［5-6］。国内外诸多学者对土壤含水量的研究非常重视［7-10］，张莉等［11］通过建立土壤含水量和光谱反射率模式方程，确定了诊断土壤水分状况的敏感波段，认为在可见光和近红外部分二者达到极显著相关，且近红外部分较为敏感。顾燕等［12］通过分析不同含水量的土壤光谱特征，建立了TM遥感影像的光谱反射率与土壤含水量的关系模型。Heike等［13］利用GeoSAIL模型，模拟了不同含水量土壤作为下垫面时，以及不同植物含水量情况下的冠层反射率，发现植被含水量变化引起的光谱差异不同于土壤含水量变化引起的光谱差异。可见，高光谱遥感能够有希望区分两者带来的影响。刘培君等［14］通过引入一个“光学植被盖度”的概念，以此来排除植被对土壤水分的干扰，使复合像元亮度变成了裸土光谱亮度，实现植被覆盖区域的土壤含水量监测。

当前国内外大都是基于土壤光谱对土壤含水量做了大量的研究，实际上由于作物冠层之下的土壤含水量动态监测对植物生长发育研究意义更为重要［15］，而基于植被冠层下不同深度土壤含水量方面的研究鲜见报道。另外，将实测高光谱数据与遥感影像数据相结合，提取土壤含水量信息仍存在困难，尺度间的数据转换成为土壤含水量遥感监测的关键。因此，本文首先通过实测植物冠层光谱反射率与土壤含水量数据的相关分析，建立实测高光谱与土壤含水量反演模型，然后，以该模型校正HSI影像建立的土壤含水量反演模型，以提高区域尺度下土壤含水量定量遥感监测精度。

1 材料与方法

1.1 研究区概况

研究区选择在库车县境内，以研究区野外实地调查采样确定边界坐标为：82°48′ ～ 83°40′E，41°5′ ～41°56′N，是典型的山前冲积扇平原，属于温带大陆性干旱气候。年平均蒸发量为1 991.0 ～ 2 864.3 mm，多年平均降水量仅为51.3 mm，主要集中在5—8月，蒸发量远大于降水量，干燥度系数为44.37，多年平均气温10.6 ～ 14.8℃，年极高、极低气温分别为41.3℃和 -28.7℃，无霜期为209.7 ～ 226.3 天，属于干旱与极端干旱地区［16］。研究区地形由三部分组成：北部海拔3 000 ～ 5 000 m的天山山脉，是重要的水源地；中部是低山和残丘；南部是山前平原区，形成和发育了较大的绿洲，是库车河沙雅经济发展的核心地带［17］。研究区植被主要以穂红柳、盐木、梭梭、盐爪爪、骆驼刺、白刺等为主，根据野外实地植被采样单元选择的典型研究区域如图1（由分别对应于HSI影像红、绿、蓝通道的12、45和90波段合成）所示。

图1 研究区地理位置图及采样点分布图Fig. 1 Geographical position map of study area and distribution of sampling sites

1.2 野外实测样本采集

为提高实测数据与影像数据在时间上的吻合性，土壤含水量数据和高光谱数据于2010年10月下旬赴研究区进行采集，数据采集时间与卫星扫描过境时间较一致。数据采集包括两部分：①表层土壤含水量数据采集：每个样方大小为30 m × 30 m，每个样方包含5个土壤采样单元和9个光谱采样单元，每个土壤采样单元分别采集土层深度为0 ～ 10（a）、10 ～ 30（b）、30 ～ 50 cm（c）3层土样，用烘干箱将土样烘干并测定土壤含水量，取5个采样单元的平均值作为本样方的土壤含水量测定值，最终获得不同深度土壤含水量数据102个；②植被冠层光谱测量：选择在晴天或云量较少时，采用ASD光谱仪（其波长包括从350 nm的可见光至2 500 nm的近红外，其中在350 ～ 1 000 nm和1 000 ～ 2 500 nm光谱采样间隔分别为1.4 nm和2 nm，光谱分辨率分别为3 nm和10 nm；最后对数据进行1 nm的重新采样［19］）于10：00—15：00（北京时间）测定植被冠层光谱，每个植被光谱采样单元中按五点梅花状进行测量，取其平均值作为该采样单元的光谱值，为了客观实际反映出典型研究区土壤含水量与植被光谱特征，确保植被冠层光谱采样单元面积与土壤采样单元面积基本相同，取9个采样单元数据的平均值作为本样方光谱数据，最终得到了与土壤采样单元相对应的34组植被反射率光谱曲线。在数据分析之前，为减少反射率曲线噪音引起的误差，对反射率曲线进行Savitzky-Golay滤波［20-21］。

1.3 HSI影像数据获取及预处理

本文使用的HSI影像数据来自中国资源卫星应用中心提供的HJ-1A星携带的高光谱成像仪（Hyperspectral imaging spectrometer），获取时间为2010年10月下旬，空间分辨率为100 m，平均光谱分辨率与ASD光谱仪光谱分辨率较为一致，为4.32 nm。土壤含水量反演之前，首先将HSI影像数据进行辐射定标等预处理；然后，将影像从DN值转化为辐射亮度值；最后，采用FLAASH模型进行大气校正，从而得到研究区影像的地表反射率值。

1.4 光谱数据处理及相关分析

在数据分析之前，对植被冠层光谱反射率数据进行光谱变换，利用相关分析数学方法，将光谱变换数据与土壤含水量数据进行分析，选择与土壤含水量响应敏感的波段，植被冠层的光谱变换包括对数、倒数、一阶微分等，相关系数jR的计算公式为：

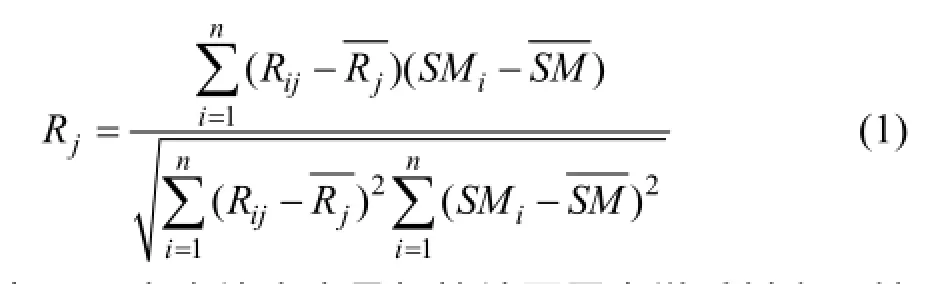
式中：Rj为土壤含水量与植被冠层光谱反射率及其光谱变换的相关系数，j为波段号，Rij是编号为i的样方在j波段的反射率及其光谱变换结果，为总数为n个的土壤采样单元光谱反射率及其光谱变换结果的平均值，SMi是编号为i的采样单元的含水量，SM为总数为n的土壤采样单元的平均含水量。

1.5 模型的建立及检验

在植被冠层光谱反射率数据及其变换和分析的基础上，采用多元逐步回归的数学方法，构建土壤含水量的反演模型。为验证模型的有效性，分别采用统计量F值和决定系数 （R2）、均方根误差RMSE （Root mean square error）来评价估算模型的精度。当F值大于理论临界值Fa时，估算精度较高；决定系数R2越接近1，估算模型方程的拟合程度越高；均方根误差用于评价估算模型方程的精度，总均方根误差越接近0，估算方程精度越高。当统计量F值大于Fa且F值越大，R2越高，RMSE越小，表明模型估算的准确性越高，反之则模型估算的准确性越差。其中，RMSE的计算公式为：

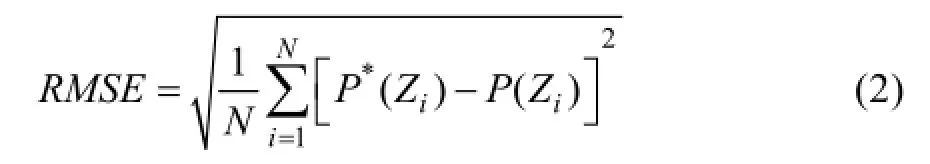
式中：P*（Zi） 表示建立模型的预测值；Z（Zi） 表示实测值；N表示样品的数量。

2 结果与讨论

2.1 不同土壤含水量的植被冠层反射率光谱特征

从采集的植被冠层原始光谱数据中剔除由于大气强吸收、水汽及其他因素干扰引起较大误差的波段。以芦苇为例说明不同土壤含水量水平下的植被冠层反射光谱曲线（图2）。可以看出，土壤含水量对芦苇冠层光谱特征有着较为明显的影响，不同土壤含水量与植被冠层光谱之间具有较高的相关性，植被冠层光谱反射率在400 ～ 750 nm与750 ～ 2 500 nm之间随着土壤含水量水平的增高而呈现递减趋势；不同土壤含水量水平的植被冠层光谱反射率在各个波段有明显差别，其中以400 ～ 650 nm附近的可见光反射峰和750 ～ 1 350 nm高反射处最为明显。

图2 不同土壤含水量水平下的植被冠层光谱曲线Fig. 2 Spectral curves under different soil moistures

2.2 实测高光谱数据分析及模型建立

将植被冠层实测高光谱反射率及其变换结果与土壤不同含水量数据作相关系数在0.01和0.05水平上的显著性检验及相关性分析，如图3所示。考虑到植被冠层实测高光谱数据与HSI影像数据的光谱分辨率大致相同（均在3 nm左右），为使得实测高光谱数据光谱波长范围与HIS影像光谱波长范围相一致，因此从实测高光谱波段中选取400 ～ 1 000 nm范围进行分析。可以看出，不同深度的土壤含水量均与光谱反射率、光谱反射率倒数、光谱反射率倒数的对数、光谱反射率对数、光谱反射率对数的倒数、光谱反射率均方根相关性较小，没有波段的相关性通过0.05水平上的显著性检验，因此不适用提取特征波段用于土壤含水量高光谱模型的建立。而除此之外的其他光谱反射率不同变换结果与土壤含水量的相关系数均有提高，部分波段相关性通过了0.01水平上的显著性检验，可以用于土壤含水量高光谱模型的建立。在此范围内逐波段筛选相关系数通过了0.01水平上的显著性检验的最高的2个波段，分别为：

1） 土壤深度为0 ～ 10 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为-0.558 1（波长483 nm）和 -0.586 0（波长911 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为 0.512 2（波长633 nm）和0.537 4（波长911 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.576 1（波长643 nm）和0.584 0（波长911 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为-0.576 1（波长643 nm）和-0.584 0（波长911 nm）；⑤光谱反射率对数的倒数一阶微分，相关系数的两个峰值分别为0.554 2（波长453 nm）和0.556 4（波长483 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.569 3（波长612 nm）和 -0.592 0（波长911 nm）。

2） 土壤深度为10 ～ 30 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为 -0.531 2（波长461 nm）和 -0.529 7（波长992 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为-0.621 7（波长459 nm）和0.601 5（波长992 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.599 7（波长461 nm）和0.611 2（波长992 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为 -0.599 7（波长461 nm）和 -0.611 3（波长992 nm）；⑤光谱反射率对数倒数一阶微分，相关系数的两个峰值分别为 -0.508 5（波长459 nm）和0.545 1（波长461 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.583 6（波长461 nm）和 -0.584 3（波长992 nm）。

3） 土壤深度为30 ～ 50 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为0.499 8（波长412 nm）和 -0.506 8（波长992 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为0.606 3（波长442 nm）和0.554 4（波长992 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.533 8（波长442 nm）和0.568 8（波长992 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为-0.533 8（波长442 nm）和-0.568 8（波长992 nm）；⑤光谱反射率对数倒数一阶微分，相关系数的两个峰值分别为 -0.482 6（波长400 nm）和 -0.476 6（波长411 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.480 5（波长862 nm）和 -0.549 9（波长992 nm）。

图3 不同土壤含水量与光谱及其变换结果的相关性分析Fig. 3 Correlation between soil moistures and spectral radiance and its transformation

以土壤含水量作为因变量，峰值波段数据作为自变量，采用多元线性回归方法，在102个不同土壤含水量数据支持下，建立实测冠层高光谱与土壤含水量的反演模型（表 1）。

表1 实测高光谱土壤含水量回归模型Table1 Soil moisture inversion model（measured hyperspectral）

由表1可以看出，植被冠层光谱反射率一阶微分模型最佳（土壤含水量深度为0 ～ 10 cm，组合波段为483 nm和911 nm），模型判定系数（R2）为0.659，并且通过Person相关系数分析，达到0.01的显著性水平。用其余光谱采样单元对模型进行检验，如图4，可以看出，验证样本判定系数（R2）为0.735 1，均方根误差（RMSE）为0.043 3，模型估算精度较好。

图4 实测土壤含水量与模型预测值比较Fig. 4 Comparison between measured and predicted values of soil moistures

2.3 HSI影像分析及模型建立

将HSI影像反射率及其变换结果与土壤不同含水量数据作相关系数在0.01和0.05水平上的显著性检验及相关性分析，如图5所示。可以看出，土壤深度为10 ～ 30 cm和30 ～ 50 cm的土壤含水量均与光谱反射率、光谱反射率倒数、光谱反射率倒数的对数、光谱反射率对数、光谱反射率对数的倒数、光谱反射率均方根相关性较小，没有波段的相关性通过0.05水平上的显著性检验，因此不适用提取特征波段用于土壤含水量高光谱模型的建立。而除此之外的其他光谱反射率不同变换结果与不同土壤含水量的相关系数均有提高，部分波段相关性通过了0.01水平上的显著性检验，可以用于土壤含水量高光谱模型的建立。在450 ～ 950 nm内逐波段筛选相关系数通过了0.01水平上的显著性检验的最高的2个波段，分别为：

1） 土壤深度为0 ～ 10 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为-0.558 1（波长552 nm）和 -0.586 0（波长555 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为0.512 2（波长900 nm）和0.537 4（波长555 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.576 1（波长460 nm）和0.584 0（波长555 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为-0.576 1（波长555 nm）和 -0.584 0（波长552 nm）；⑤光谱反射率对数的倒数一阶微分，相关系数的两个峰值分别为0.554 2（波长555 nm）和0.556 4（波长552 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.569 3（波长555 nm）和 -0.592 0（波长460 nm）。

2） 土壤深度为10 ～ 30 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为 -0.531 2（波长748 nm）和 -0.529 7（波长841 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为-0.621 7（波长841 nm）和0.601 5（波长748 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.599 8（波长841 nm）和0.611 2（波长748 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为 -0.599 7（波长841 nm）和 -0.611 3（波长748 nm）；⑤光谱反射率对数倒数一阶微分，相关系数的两个峰值分别为-0.508 5（波长748 nm）和0.545 1（波长841 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.583 6（波长841 nm）和 -0.584 3（波长748 nm）。

3） 土壤深度为30 ～ 50 cm分别为：①光谱反射率一阶微分，相关系数的两个峰值分别为0.499 8（波长549 nm）和 -0.506 8（波长496 nm）；②光谱反射率倒数一阶微分，相关系数的两个峰值分别为0.606 3（波长841 nm）和0.554 4（波长652 nm）；③光谱反射率倒数的对数一阶微分，相关系数的两个峰值分别为0.533 8（波长841 nm）和0.568 8（波长496 nm）；④光谱反射率对数一阶微分，相关系数的两个峰值分别为-0.533 8（波长841 nm）和-0.568 8（波长496 nm）；⑤光谱反射率对数倒数一阶微分，相关系数的两个峰值分别为 -0.482 6（波长549 nm）和 -0.476 6（波长496 nm）；⑥光谱反射率均方根一阶微分，相关系数的两个峰值分别为 -0.480 5（波长549 nm）和 -0.549 9（波长496 nm）。

图5 植被冠层光谱数据与土壤含水量相关分析Fig. 5 Correlation analysis of vegetation canopy spectral data and soil moisture

同样以土壤含水量作为因变量，峰值波段数据作为自变量，采用多元线性回归方法，在102个不同土壤含水量数据支持下，建立HSI影像与土壤含水量的反演模型（表2）。

表2 HSI影像土壤含水量回归模型Table2 Soil moisture inversion model （HSI）

由表2可以看出，HSI影像光谱反射率对数一阶微分模型最佳（土壤含水量深度为0 ～ 10 cm，组合波段为555 nm和552 nm），模型判定系数（R2）为0.557，并且通过Pearson相关系数分析，达到0.01的显著性水平。用其余光谱采样单元对模型进行检验，如图6，可以看出，验证样本判定系数（R2）为0.623，均方根误差（RMSE）为0.051 8，模型估算精度较植被冠层光谱模型差。

2.4 模型校正与检验

为了提高反演模型精度并且更好地结合HIS影像数据进行分析，寻求实测冠层光谱反射率及其变换结果数据与HSI影像数据之间的关系，将实测高光谱数据与HSI影像数据之间建立联系方程，如图7所示，用实测高光谱土壤含水量反演模型校正HSI影像土壤含水量反演模型。

经过实测高光谱土壤含水量反演模型校正的HSI影像土壤含水量反演模型检验结果如图8所示，可以看出，模型判定系数R2得到了较好的提高，由0.549提升到0.719，且通过了0.01的显著性水平，RMSE值为0.043 5。因此，校正后的HSI影像土壤含水量反演模型能够较好地提高区域尺度条件下表层土壤含水量监测精度。图9为典型研究区土壤深度为0 ～10 cm的土壤含水量空间分布。

图6 估测值与实测值比较Fig. 6 Comparison between predicted and measured values of soil moistures

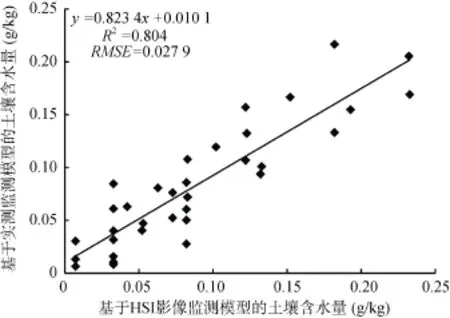
图7 实测高光谱土壤含水量反演模型与HSI影像土壤含水量反演模型散点图Fig. 7 Scatterplot of measured hyperspectral soil moisture inversion model and HSI soil moisture inversion model

图8 校正后的模型与实测含水量比较Fig. 8 Comparison between predicted and measured values of soil moistures after calibration

图9 研究区0 ～ 10 cm土壤含水量空间分布图Fig. 9 Soil moisture space distribution of studied area in 0-10 cm layer

3 结论

1） 土壤含水量的敏感波段区域为450 ～ 650 nm和850 ～ 920 nm。

2） 实测冠层高光谱土壤含水量反演模型中，以土壤深度为0 ～ 10 cm的冠层光谱反射率一阶微分模型最佳，波段组合为483 nm和911 nm，模型通过0.01显著性水平检验，判定系数R2为0.735，均方根误差（RMSE）为0.043 3 。

3） HSI高光谱影像土壤含水量反演模型中，以土壤深度为0 ～ 10 cm的冠层光谱反射率对数一阶微分模型最佳，波段组合为552 nm和555 nm，模型通过0.01显著性水平检验，判定系数R2为0.623，均方根误差（RMSE）为0.051 8。

4） 校正后的HSI高光谱影像土壤含水量反演模型，模型判定系数R2得到了较好的提高，由0.549提升到0.719，且通过了0.01的显著性水平，RMSE值为0.043 5。

以上结论表明冠层高光谱土壤含水量反演模型和HSI影像土壤含水量反演模型对于0 ～ 10 cm深度的土壤含水量效果较好，30 ～ 50 cm效果最不理想。同时，经过校正的HSI 影像土壤含水量反演模型，能够在一定区域尺度条件下较好提高模型对土壤含水量的监测精度，因此运用此方法进行区域土壤含水量定量遥感监测研究是可行的，这在土壤含水量高光谱估算模型由点及面的尺度转换研究方面做了初步探索研究。由于HSI影像的空间分辨率较低以及限于单一年份的试验数据，因此土壤含水量反演模型具有一定的局限性，必然影响模型的监测精度，在以后的研究中采用多年试验数据及更高空间分辨率的高光谱影像进行研究和验证，将会更好地进行土壤含水量定量遥感监测。

［1］ 李玲芬， 延军平， 刘冬梅， 等. 干旱-半干旱地区不同植被条件下土壤含水量变化及植被建设途径分析［J］. 水土保持通报， 2009， 29（1）： 18-22

［2］ 张素芳， 马礼. 坝上高原林草地表层土壤含水量对比研究［J］. 干旱区资源与环境， 2013， 27（2）： 167-170

［3］ 李萍， 赵庚星， 高明秀， 等. 黄河三角洲土壤含水量状况的高光谱估测与遥感反演［J］. 土壤学报， 2015， 52（6）：1 262-1 272

［4］ Bach H， Mauser W. Modelling and model verification of the spectral reflectance of soils under varying moisture conditions［J］. Geoscience and Remote Sensing Symposium，1994， 4： 2 354-2 356

［5］ Ben-Dor E， Patin K， Banin A， et al. Mapping of several soil properties using DAIS-7915 hyperspectral scanner data —a case study over clayey soils in Israel［J］. International Journal of Remote Sensing， 2002， 23（6）： 1 043-1 062

［6］ Lu N， Zhang Z， Gao Y. Recognition and mapping of soil salinization in arid environment with hyperspectral data［J］. Geoscience and Remote Sensing Symposium， 2005， 6： 4 520-4 523

［7］ 张继光， 陈洪松， 苏以荣， 等. 喀斯特山区洼地表层土壤水分的时空变异［J］. 生态学报， 2008， 28（12）： 6 334-6 343

［8］ 赵纯， 袁国富， 刘晓， 等. 宇宙射线土壤水分观测方法在黄土高原草地植被的应用［J］. 土壤学报， 2015， 52（6）：1 439-1 444

［9］ 曹丽花， 刘合满， 赵世伟. 当雄草原不同退化草甸土壤含水量及容重分布特征［J］. 草业学报， 2011， 19（5）： 746-751

［10］ 刘凯， 高磊， 彭新华， 等. 半干旱区科尔沁沙地土壤水分时空特征研究［J］. 土壤， 2015， 47（4）： 765-772

［11］ 张莉， 孙虎. 黄土高原地区土壤含水量与反射光谱关系研究［J］. 土壤通报， 2009， 40（6）： 1 255-1 258

［12］ 顾燕， 张鹰， 李欢， 等. 基于实测光谱的潮滩土壤含水量遥感反演模型研究［J］. 湿地科学， 2013， 11（2）： 167-172

［13］ Bach H， Verhoef W. Sensitivity studies on the effect of surface soil moisture on canopy reflectance using the radiative transfer model GeoSAIL［J］. IEEE International Geoscience & Remote Sensing Symposium 2003， 3：1 679-1 681

［14］ 刘培君， 张琳， 艾里西尔·库尔班， 等. 卫星遥感估测土壤水分的一种方法［J］. 遥感学报， 1997， 1（2）： 135-138

［15］ 徐希孺， 周莲芳， 朱晓红. 混合像元的因子分析方法及其在大范围冬小麦播种面积估算中的应用探讨［J］. 科学通报， 1989， 34（12）： 946-949

［16］ 张飞， 塔西甫拉提特依拜， 孔祥德， 等. 干旱区绿洲土地利用景观空间格局动态变化研究：以渭干河-库车河三角洲绿洲为例［J］. 资源科学， 2006， 28（6）： 167-174

［17］ 满苏尔·沙比提， 楚新正. 新疆渭干河一库车河三角洲绿洲土地利用时空变化特征分析［J］. 干旱地区农业研究，2007， 25（4）： 12-18

［18］ 彭杰， 王家强， 向红英， 等. 土壤含盐量与电导率的高光谱反演精度对比研究［J］. 光谱学与光谱学分析， 2014，34（2）： 510-514

［19］ 刘炜， 常庆瑞， 郭曼， 等. 不同尺度的微分窗口下土壤有机质的一阶导数光谱响应特征分析［J］. 红外与毫米波学报， 2011， 30（4）： 316-321

［20］ Savizky A， Golay M J E. Smoothing and differentiation of data by simplified least squares procedures［J］. Analytical Chemistry， 1964， 36（8）： 1 627-1 639

［21］ 朱西存， 赵庚星， 雷彤. 苹果花期冠层反射光谱特征［J］.农业工程学报， 2009， 25（12）： 180-186

Study on Soil Moisture Monitoring Base on Measured Hyperspectral and HSI Data

LI Xiang1，2， DING Jianli1，2*， HUANG Shuai1，2， CHEN Wenqian1，2， WANG Jiao1，2， YUAN Ze1，2， CHEN Yun3
（1 College of Research and Environment Science， Xinjiang University， Urumqi 830046， China； 2 Key Laboratory of Oasis Ecology， Ministry of Education， Xinjiang University， Urumqi 830046， China； 3 CSIRO Land and Water of Australia， Canberra VIC 3169， Austrilia）

Based on measured vegetation canopy hyperspectral data and HSI hyperspectral image data in a typical region，sensitive bands to soil moisture in different soil depths were selected by correlation analyses to establish the optimal inversion model of soil moisture by HSI image data， and the inversion model was calibrated by HSI inversion model based on the measured soil moisture. The results showed that： the sensitive bands to soil moisture were in 450 - 650 nm and in 850 - 920 nm； the two soil moisture inversion models showed that： the estimation effect for soil moisture in 0 - 10 cm depth was the best， and the accuracy of the inversion model based on HSI image data was higher than the inversion model based on the measured hyperspectral data， and the coefficients of determination （R2） were 0.659 and 0.557， respectively； the accuracy of soil moisture inversion model was improved better after calibration， the coefficient of determination （R2） raised to 0.719 from 0.557， and root mean square error （RMSE） was of 0.043 5， which indicated that the improvement of monitoring accuracy on soil moisture at the regional scale and proved this technique is feasible to monitor soil moisture， and provided helps to further improve soil moisture monitoring by remote sensing at regional scale.

Hyperspectral； Soil moisture； HSI image； Multiple linear regression

S127；S152.7

10.13758/j.cnki.tr.2016.05.027

自治区科技支疆项目（201591101）、国家自然科学基金项目（U1303381、41261090、41161063）、教育部促进与美大地区科研合作与高层次人才培养项目和2015年新疆维吾尔自治区研究生科研创新项目（XJGRI2015018）资助。

*通讯作者（ding_jl@163.com）

李相（1991—），男，河南永城人，硕士研究生，主要研究方向为生态与遥感。E-mail： lixiang91526@163.com