无线通信调制信号的信息安全风险分析

魏 冬 刘 博 梁莉莉 李 敏

1(中国科学院信息工程研究所 北京 100093)2 (国家保密科技测评中心 北京 100044)



无线通信调制信号的信息安全风险分析

魏 冬1刘 博2梁莉莉1李 敏1

1(中国科学院信息工程研究所 北京 100093)2(国家保密科技测评中心 北京 100044)

(weidong@iie.ac.cn)

无线通信已深入到人们工作和生活的各个方面，其安全性问题不容忽视.由于无线通信物理信道的开放性，承载着重要信息的调制信号完全暴露在自由空间中，而当前的无线通信系统却十分缺少物理层方面的防护措施，攻击者可以利用盲信号处理技术恢复出信号的重要信息，从而使得合法通信遭受巨大威胁.围绕无线通信中调制信号信息安全风险问题展开分析，首先介绍了非协作通信环境中调制信号的重要信息的恢复方法，然后通过仿真实验对其安全风险进行了定性评估.

无线通信；物理层安全；非协作通信；盲信号处理；定性评估

通信与人类的生活息息相关，从日常发送一个短信息到两国电子战中截获敌方情报，都离不开有效的通信.无线通信由于不用架线、灵活性强等特点而被广泛应用，如今每天大约有15万人成为新的无线用户，全球范围内的无线用户数量现今已经超过2亿，涉及到人们生活和工作的各个方面，其中3G、WLAN、蓝牙、数字电视及宽带卫星系统等都是21世纪最热门的无线通信技术应用.然而由于无线通信系统信道的开放性，其安全性从技术诞生起就是工程技术人员必须面对的问题[1].在无线通信中，自由空间传输的是高频调制信号.在物理层中，待发送的数据利用调制技术形成高频调制信号，调制信号承载的信息与发送数据是密切相关的，被用来解调信号及恢复发送序列.由于无线通信链路的开放性，承载着重要信息的调制信号完全暴露在电磁空间中，任何人都可以接收这些调制信号，因此无线通信存在信息安全隐患.在当前无线通信系统中被广泛应用的安全防护措施建立在链路层或应用层，通过一定的密码算法对信息流进行加密，建立在物理层之上，假设物理层无差错传输[1-2].事实上，无线物理信道的开放性为攻击者窃密提供了极大便利，攻击者截获这些调制信号，利用信道均衡、调制识别等盲信号处理技术即可获得信号的关键信息[3]，进而推测用户身份，甚至破译截获信号所承载的明文信息，使合法用户的通信安全遭受巨大威胁.

本文围绕无线通信系统中调制信号的信息安全风险问题展开分析，首先分析了无线通信系统发送与接收模型，对调制在系统中的作用及其重要性进行了阐述；然后介绍了实际非协作通信环境中没有任何先验知识的情况下调制信号重要信息的恢复方法，说明了无线通信调制信号信息存在安全风险；在此基础上以无线通信系统中常用的调制信号为例，通过仿真对其信息安全风险进行了定性分析；最后是结论部分.

1 无线通信系统模型分析

无线通信系统的传输媒介是自由空间，图1为无线通信系统发送与接收模型.

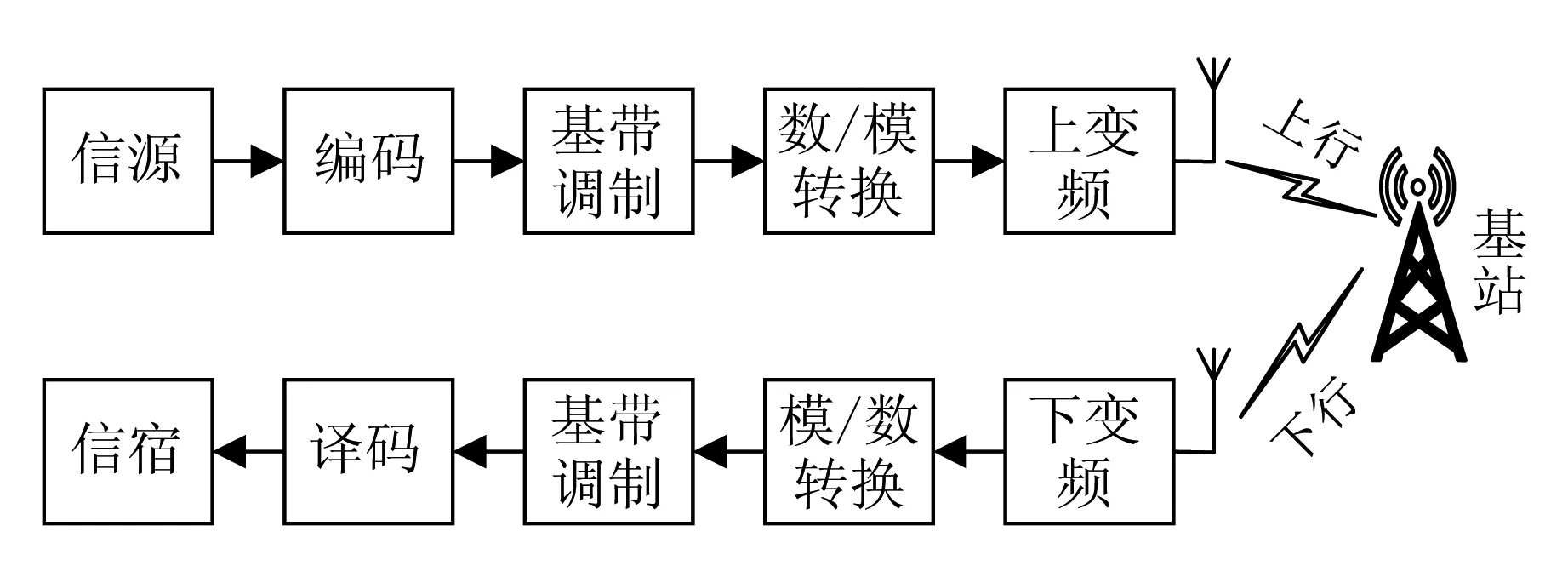
图1 无线通信系统发送与接收模型

在无线通信系统发送与接收模型中，二进制数据经过信源编码与信道编码后，进行基带调制和数模转换变成基带模拟信号，再上变频至射频，最后进行功率放大并天线发射，经过基站转发在接收端利用天线接收，经过模数转换、基带解调、信道与信源译码恢复发送数据.传输过程中必然引入干扰，为了分析方便，把通信系统中各种设备以及信道中所固有的噪声干扰集中加入到传输媒介中.

其中，调制过程由映射和调制2个独立步骤实现.映射将多个比特转换为1个多元符号，这种多元符号可以是实数信号，也可以是2维平面的复信号.信息与信号间的映射方式可以有很多种，不同的通信技术就在于它们所采用的映射方式不同.而数字调制是按照特定的映射规则改变信号的幅度、相位和频率，使其按照将要传输信号的特点变化而变化.调制信号承载着与发送数据密切相关的重要信息，包括信号的瞬时特征(幅度、相位、频率等)、统计特征(高阶累积量、循环累积量等)及调制参数(符号率、调制方式、调制阶数等)，有效利用这些信息即可实现对信号的解调译码.

从无线通信系统的模型可以看出，由最初的发送数据转变到最终发射的载波信号最关键的部分在于调制部分，通过映射与调制使调制信号有效地承载了发送信息.同样在接收模型中，信号经过下变频和模数转换后变成基带信号，需要按照同样的映射规则对信号解调才能进一步实现译码得到发送数据，因此信号承载的信息对通信双方是极其重要的.

2 无线通信调制信号的信息安全风险分析

在无线通信系统中，由于无线通信链路的开放性，承载着重要信息的无线调制信号完全暴露在自由的电磁空间中，使得无线通信存在很大的安全风险.一方面，任何人都可以利用接收设备截获自由空间中的信号，开放的无线通信链路为攻击者窃密提供了便利；另一方面，目前的无线通信系统缺少物理层安全防护措施，而信道均衡、调制识别等盲信号处理技术已比较成熟，即使在没有任何关于发送信号的先验知识的情况下，攻击者利用相关技术依然能够得到所截获调制信号的重要信息，甚至实现对信号的解调译码.

本文针对无线通信调制信号的信息安全风险进行研究.考虑到信号的瞬时特征直接承载着发送的基带信号信息，信号的星座图完整、清晰地表达了数字调制的映射关系，且很多调制识别方法均是基于这些特征进行研究的[4]，为验证无线通信调制信号存在的信息安全风险问题，接下来将简单分析如何在实际非协作通信中恢复调制信号的重要信息，包括信号的瞬时幅度、瞬时相位、瞬时频率及信号的星座图.

在实际应用中，利用频谱分析仪等接收仪器可以监测到一定频谱带宽的信号，可以人工近似估计感兴趣频段信号的中心频率，对信号进行正交下变频采集得到I路和Q路基带信号.由于缺少先验知识以及硬件设备精度限制，估计的中心频率与发送信号的载波频率存在偏差，使得采集到的I(t)和Q(t)并不是理想的基带信号，而含有一定的载波频率偏差Δf，因此接收复信号可表示为：

Y(t)=I(t)+jQ(t)=Al(t)ej(φl(t)+2πΔft),

(1)

其中，Al(t)和φl(t)分别是中心频率为0的基带信号的幅度和相位，含有噪声干扰.在本文中，基带信号均指中心频率为0的信号.

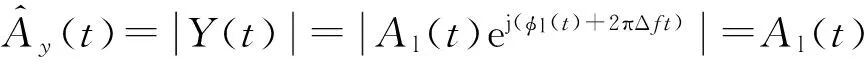
(2)

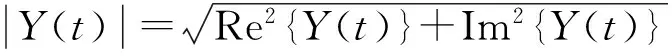
可见信号幅度是非负的.

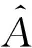
接收信号的瞬时相位φy(t)和基带信号瞬时相位φl(t)满足如下关系：

φy(t)=φl(t)+2πΔft.

(3)

从式(3)可以看出，载波频偏的存在为接收信号的瞬时相位φy(t)引入了线性相位分量2πΔft，因此得到接收信号的相位后需要去除该线性相位分量才能得到基带信号的瞬时相位[5-6].

φ(t)=

(4)

由式(3)可知，由于载频偏差的存在，瞬时相位的绝对大小会随着采样时间增大，当相位真值小于0或者大于等于2π时，按式(4)计算的相位φ(t)是相位真值φy(t)模2π后的结果，因而会造成相位卷叠.

这里选用给相位φ(t)加上校正相位分量{Ck(t)}的去卷叠算法，具体计算如下：

Ck(t)=

(5)

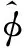
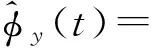
(6)

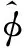
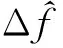
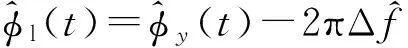
(7)

结合式(4)～(7)，无需任何先验知识即可估计出基带信号的瞬时相位.

瞬时频率的概念由Carson等人[9]于1937年首次在电路理论中提出，指出瞬时频率是传统频率的一般化，是相位角对于时间的变化率，1946年Gabor[10]给出了经典解析信号的定义，为研究瞬时频率提供了理论基础.目前常见的瞬时频率估计方法有相位法、谱峰检测法及过零点法等[11].其中相位差分法是一种常用的传统的瞬时频率估计方法，计算公式如式(8)：

(8)

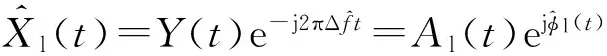
(9)

由信号瞬时幅度和瞬时相位的估计值可得到与式(9)相同的基带信号表达式.

在估计出基带信号后，将恢复出的复基带信号的实部和虚部分别作为2维复平面的横、纵坐标即可得到信号的星座图.为计算统一，将信号能量进行归一化.

若要实现信号的调制方式及调制阶数的自动识别，还需要对恢复出的星座点进行聚类，目前常用的有K均值聚类和减法聚类等.有时，为了减小多径干扰等影响，在星座图恢复之前需进行信道盲均衡处理[12].

综上，由于缺少对物理层调制过程中重要信息的安全防护措施，即使在没有任何先验知识的非协作通信情况下，信号的重要信息依然可以被恢复出来，使通信存在极大的安全隐患.

3 仿真与分析

为对无线通信调制信号的信息安全风险进行定性分析，本文选取数字移动通信、卫星通信、蜂窝集群通信等无线通信领域中常用到的GMSK(Gaussian filtered minimum shift keying)，QPSK(quadrature phase shift keying)，16QAM(16 quadrature amplitude modulation)信号进行仿真分析.所有仿真实验均假设为非协作通信环境，没有用到任何先验知识，其中噪声均为加性高斯白噪声，观察码元个数为N，采样周期Ts=11600 s，码元周期T=1200 s，载频偏差ΔfT=0.1.

对于GMSK信号，成形滤波器为高斯滤波器，其中滤波器的3 dB带宽和符号码元周期的乘积为0.5.GMSK信号的2个基带载频分别为f1=1(4T)=50 Hz，f2=-1(4T)=-50 Hz.考虑到GMSK信号调制特征是瞬时频率，因此本文依据瞬时频率的估计效果对其存在的信息安全风险进行定性分析.

图2和图3分别为信噪比为30 dB和15 dB、观察码元个数为300时利用相位差分法估计的GMSK信号瞬时频率.

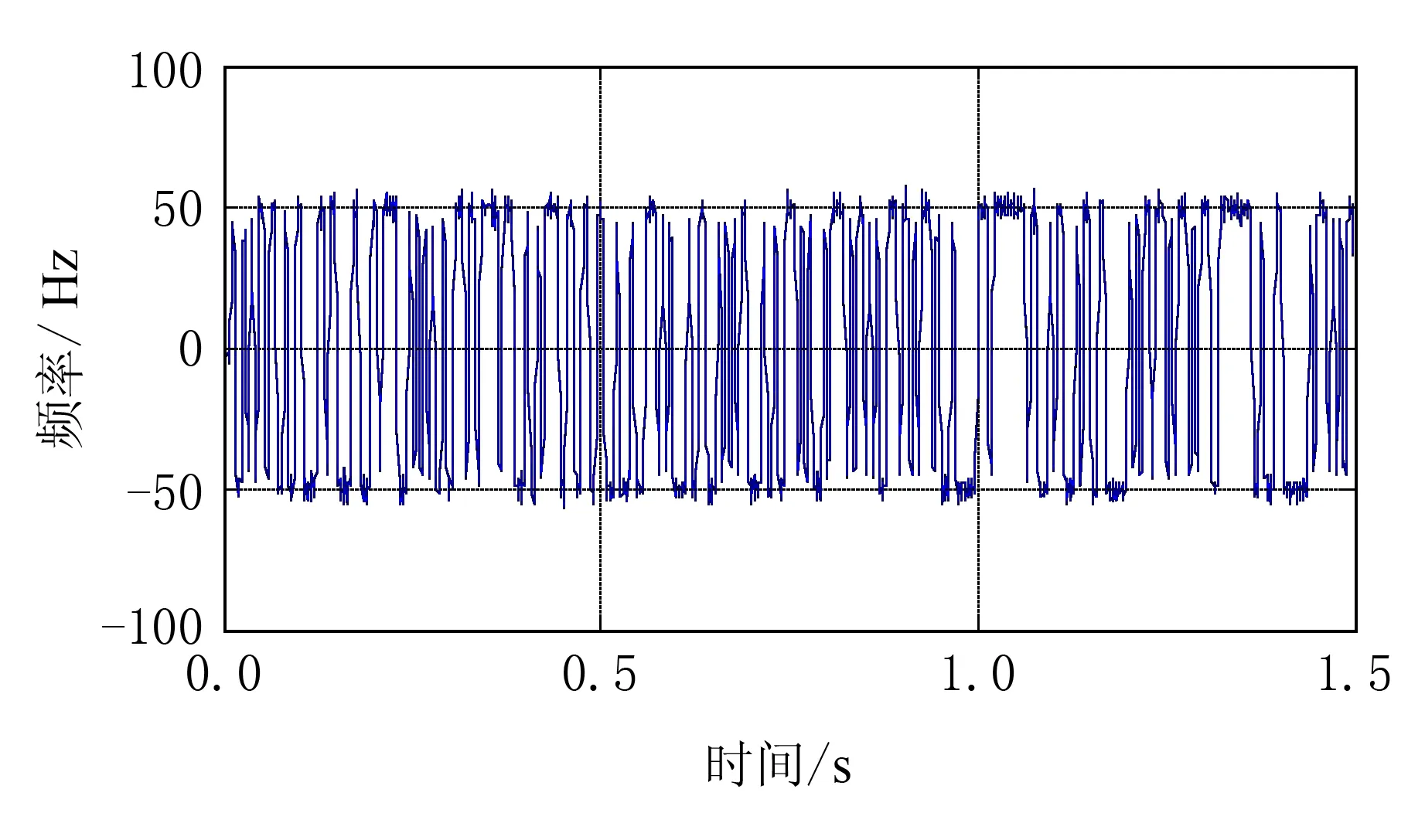
图2 信噪比为30 dB,N=300时GMSK信号瞬时频率

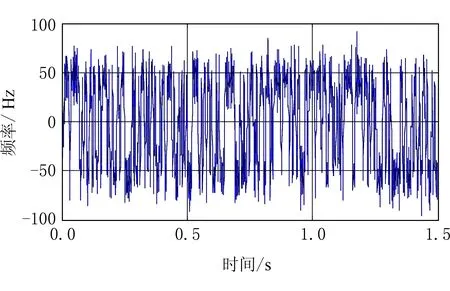
图3 信噪比为15 dB,N=300时GMSK信号瞬时频率

从图2可以清晰地看到恢复出的信号频率主要有2种，即50 Hz和-50 Hz，与理论分析一致.图3表明当信噪比下降到15 dB时，瞬时频率估计效果下降，毛刺增大，但仍能够恢复出正确的瞬时频率.效果变差是由于直接相位差分法对噪声的敏感性导致的，可以采用加平滑窗或时间变化操作减小相位差分估计误差[11].图2和图3表明，非协作通信环境下，利用相位差分法可以准确恢复出较高信噪比下的信号瞬时频率，并可通过一些改进算法修正低信噪比时的瞬时频率毛刺问题，GMSK调制信号的重要信息在高信噪比时存在较大的安全风险.

对于QPSK和16QAM信号，成形滤波器选为升余弦成形滤波，滚降因子为0.35.考虑到PSK和QAM信号的调制特征为瞬时相位和幅度，因此针对这2类信号，本文依据信号的星座图恢复效果包括聚类点数及结构分布等，对其存在的信息安全风险进行定性分析.

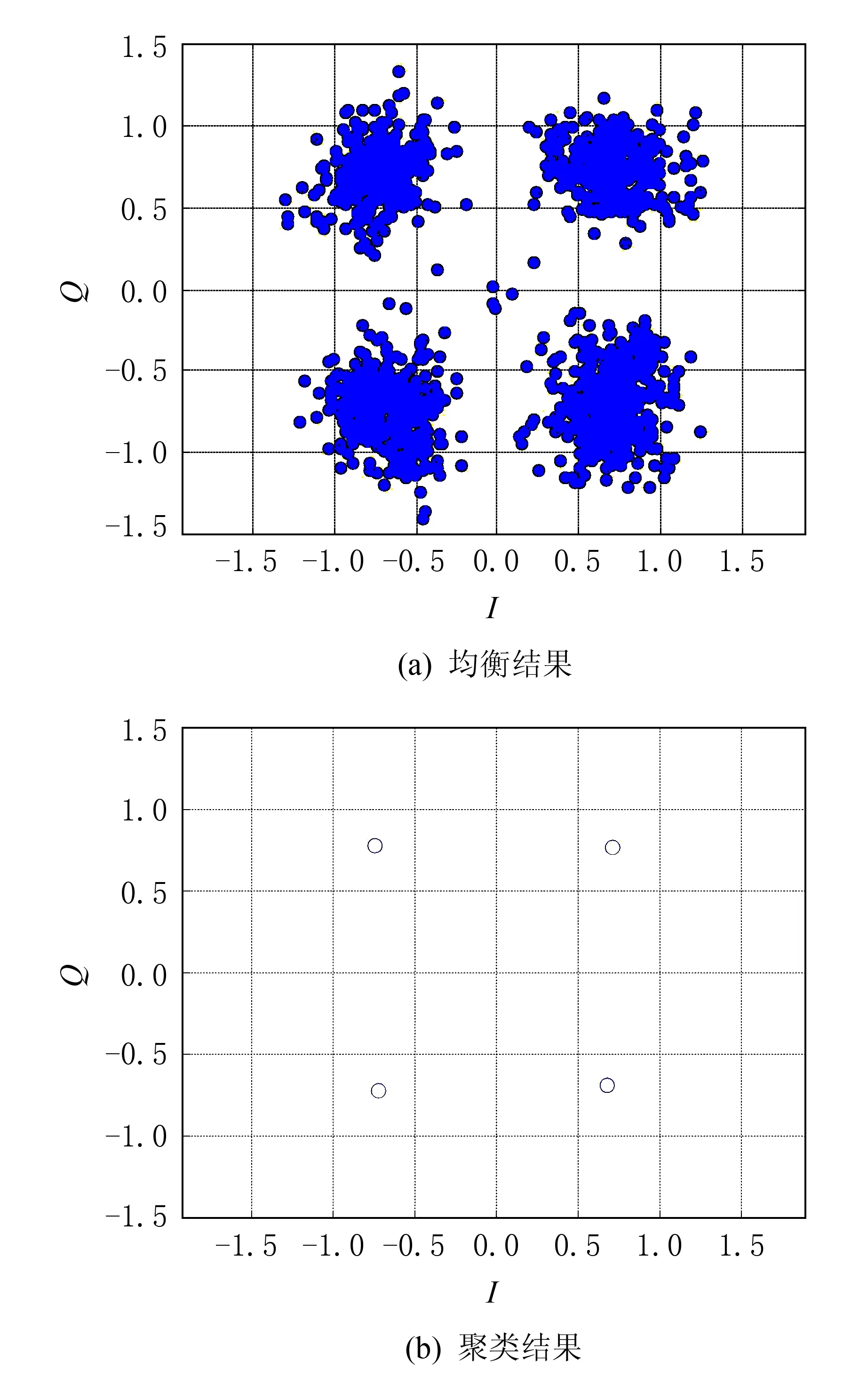
图4 信噪比为6 dB，N=300时QPSK星座图恢复效果

图4为在信噪比为6 dB、观察码元个数为300时QPSK信号星座图恢复结果，采用了基于2阶统计量的信道盲均衡算法和减法聚类算法[12]，其中图4(a)为恢复出的信号星座图，图4(b)为其对应的聚类后的结果.

图5为在信噪比为2 dB、观察码元个数为300时QPSK信号的星座图恢复结果，其他条件不变.

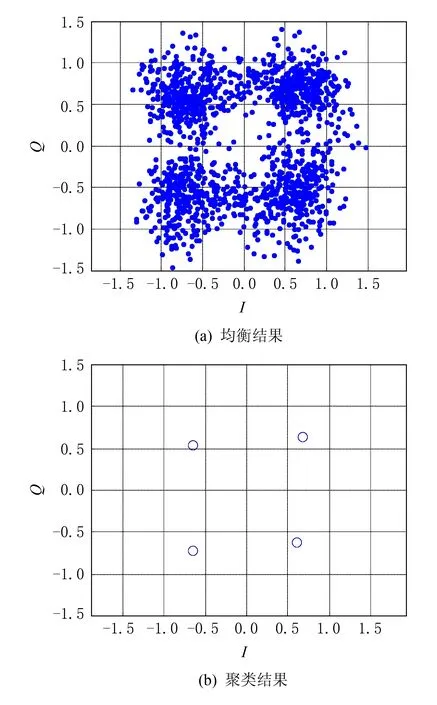
图5 信噪比为2 dB，N=300时QPSK星座图恢复效果

从图4和图5可以看出，随着信噪比的降低，星座图形状变得杂散，但在信噪比为2 dB、观察码元个数为300时依然能够得到比较清晰的QPSK信号星座图及正确的聚类个数.

当信噪比为0 dB、观察码元个数为300时得不到正确的聚类结果，增大观察码元个数为600，其他条件不变，QPSK星座图恢复结果如图6所示.

图6 信噪比为0 dB，N=600时QPSK星座图恢复效果

在图6中，QPSK信号的星座图聚类点数正确，但结构有一定变形，该问题可通过增大观察码元个数改善.可以看出，即使信噪比很低(低于2 dB)时，QPSK信号的星座图仍能被正确地恢复出来，另外，从信号的星座图还可以得到调制信号的映射规则、调制方式及调制阶数等重要信息，因此QPSK调制信号重要信息存在很大的安全风险.

图7为在信噪比为6 dB、观察码元个数为1 000时恢复出的16QAM信号星座图恢复结果，其他条件不变.

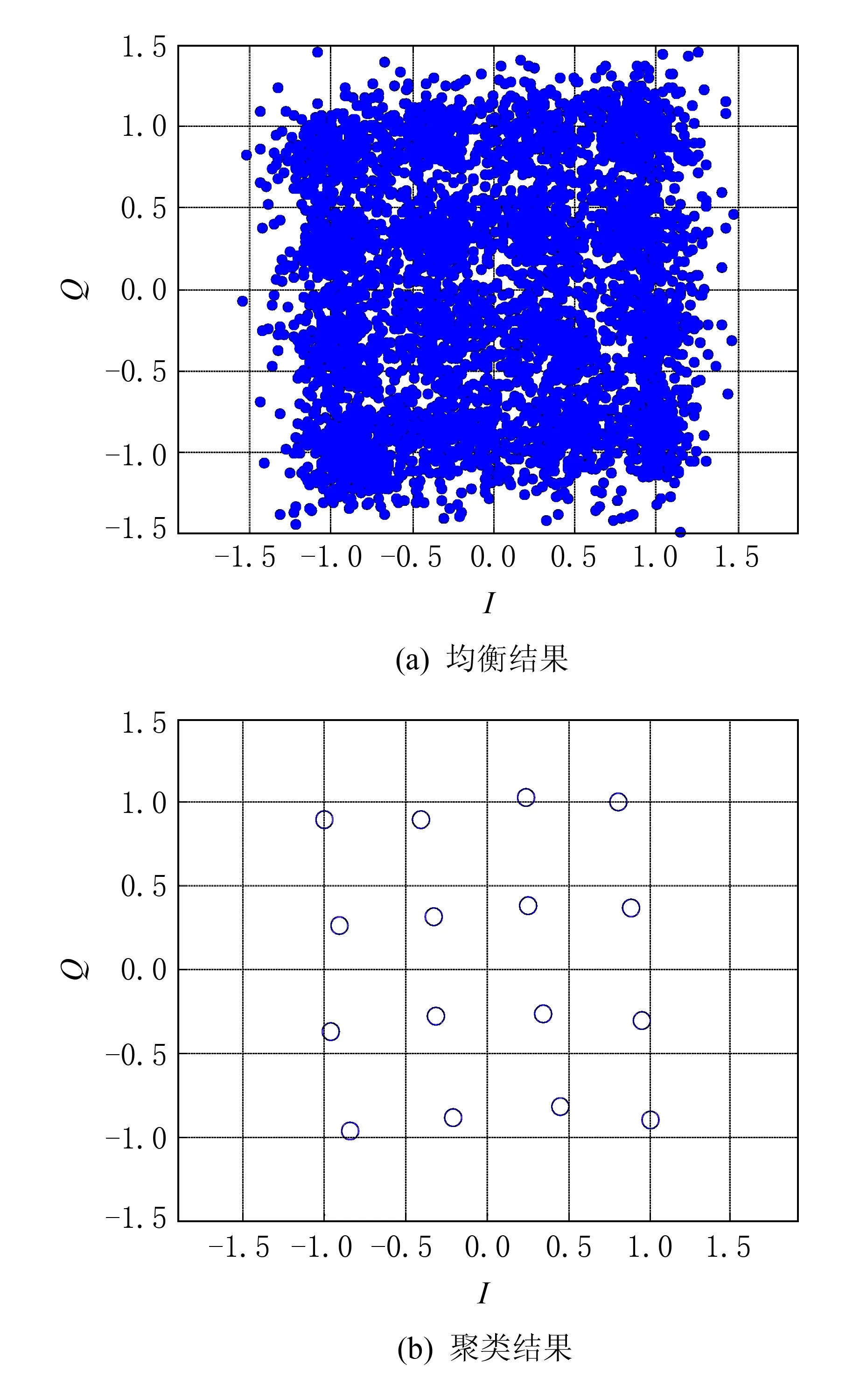
图7 信噪比为6 dB，N=1 000时16QAM星座图恢复效果

从图7中可以看出，信号星座图整体旋转了一个角度，这是载波相位引起的，可以通过载波相位估计算法对其进行消除[13].

由于16QAM信号比QPSK信号星座点数增多，星座点间的最小欧氏距离变小，因此相比QPSK信号，16QAM信号需要更多的观察码元个数和更高的信噪比才能得到同等理想的星座图恢复效果，这是符合理论分析的.

综上可知，在没有任何先验信息时，在一定的信噪比和观察码元个数情况下，常规调制信号的基本瞬时特征及星座图等重要信息能够被恢复出来，若结合通信信号调制方式识别、码元同步等技术即可对接收信号进行盲解调，从而使合法通信遭受安全威胁.

调制方式加密技术是近年来新出现的物理层加密技术[14-15]，基本思想是在基带数字调制时对信息比特映射星座符号的形式进行加密，通过改变星座图结构，如对旋转、扰乱或引入极化状态调制[16]等，使星座图不再具有常规信号星座图的规律性，实现对调制过程中关键信息的隐藏及防护，使攻击者无法进行正确解调.

4 结束语

本文通过分析在没有任何先验知识的非协作通信环境中调制信号的重要信息的恢复方法与仿真实验，对无线通信调制信号的信息安全风险进行了定性分析与评估.仿真实验表明，由于无线通信链路的开放性和调制信号重要信息防护技术应用的缺乏，常规调制信号(GMSK，QPSK，16QAM等)存在较大的信息安全风险，信号的重要信息很容易被攻击者利用盲信号处理技术恢复出来，尤其在接收信噪比较高时能够得到完整、清晰的信号特征，进而使通信安全遭受极大威胁，因此在无线通信系统中，对物理层上信号的调制过程进行安全防护是十分必要的.

[1]杨斌. 无线通信物理层安全技术研究[J]. 信息网络安全, 2012 (6): 76-79

[2]刘在爽, 王坚, 孙瑞, 等. 无线通信物理层安全技术综述[J]. 通信技术, 2014, 47(2): 128-135

[3]许小东. 非协作数字通信系统盲解调关键技术研究[D]. 合肥: 中国科学技术大学, 2007

[4]Dobre O A, Abdi A, Bar-Ness Y, et al. Survey of automatic modulation classification techniques: Classical approaches and new trends[J]. Iet Communications, 2007, 1(2): 137-156

[5]Nandi A K, Azzouz E E. Automatic modulation recognition of communication signals[J]. IEEE Trans on Communications, 1998, 46(4): 431-436

[6]阙隆树, 冯全源. 数字调制信号识别中的相位去卷叠门限研究[J]. 信号处理, 2010, 26(1): 56-59

[7]Mengali U, Morelli M. Data-aided frequency estimation for burst digital transmission[J]. IEEE Trans on Communications, 1997, 45(1): 23-25

[8]Ghogho M, Swami A, Durrani T. Blind estimation of frequency offset in the presence of unknown multipath[C]Proc of 2000 IEEE Int Conf on Personal Wireless Communications. Piscataway, NJ: IEEE, 2000: 104-108

[9]Carson J R, Fry T C. Variable frequency electric circuit theory with application to the theory of frequency-modulation[J]. Bell System Technical Journal, 1937, 16(4): 513-540

[10]Gabor D. Theory of communication. Part 1: The analysis of information[J]. Journal of the Institution of Electrical Engineers—Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429-441

[11]陈平, 李庆民, 赵彤. 瞬时频率估计算法研究进展综述[J]. 电测与仪表, 2006, 43(7): 1-7

[12]王建新, 宋辉. 基于星座图的数字调制方式识别[J]. 通信学报, 2004, 25(6): 166-173

[13]Serpedin E, Ciblat P, Giannakis G B, et al. Performance analysis of blind carrier phase estimators for general QAM constellations[J]. IEEE Trans on Signal Processing, 2001, 49(8): 1816-1823

[14]Tahir M, Jarot S P W, Siddiqi M U. Wireless physical layer security using encryption and channel pre-compensation[C]Proc of 2010 IEEE Int Conf on Computer Applications and Industrial Electronics. Piscataway, NJ: IEEE, 2010: 304-309

[15]Ma R, Dai L, Wang Z, et al. Secure communication in TDS-OFDM system using constellation rotation and noise insertion[J]. IEEE Trans on Consumer Electronics, 2010, 56(3): 1328-1332

[16]魏冬, 孔斌, 乔荣, 等. 基于极化状态-幅度-相位调制的高效无线传输方案[J]. 中国科学: 信息科学, 2015, 45(10): 1263-1279

魏 冬

助理研究员，主要研究方向为无线通信物理层安全、信号处理.

weidong@iie.ac.cn

刘 博

工程师，主要研究方向为云计算、虚拟化、网络可靠性与可用性分析、计算机应用与可靠性工程等.

bobov66@163.com

梁莉莉

硕士研究生，主要研究方向为无线通信物理层安全、信号处理.

lianglili@iie.ac.cn

李 敏

高级工程师，硕士生导师，主要研究方向为网络安全、电磁安全与防护.

limin@iie.ac.cn

Modulated Signal Information Security Risk Analysis in Wireless Communications

Wei Dong1, Liu Bo2, Liang Lili1, and Li Min1

1(InstituteofInformationEngineering,ChineseAcademyofSciences,Beijing100093)2(NationalSecrecyScienceandTechnologyEvaluationCenter,Beijing100044)

Wireless communications have gone deep into every aspect of people’s work and lives, but its security cannot be overlooked. Due to the openness of the physical channel in wireless communications, modulated signals carrying important information are completely exposed in free space. However, there are few protective measures for the modulated information at the physical layer in current wireless communication systems so that an attacker can use blind signal processing technique to recover important information of signals and make legal communications suffer huge security threats. The paper focuses on the modulated signal information security risk analysis in wireless communications. Recovery methods of important modulated signal features in non-cooperative communications, including instantaneous features and constellation diagram, are introduced first, then qualitative risk assessments for the key features of modulated signals are made by simulating analysis.

wireless communications; physical layer security; non-cooperative communications; blind signal processing; qualitative assessments

2015-01-10

国家自然科学基金项目(61501458)

TN918