Indirect Radau pseudospectral method for the receding horizon control problem

Lio Yuxin,Li Huifeng,Bo Weimin,b

aSchool of Astronautics,Beihang University,Beijing 100083,ChinabScience and Technology Committee,China Aerospace Science and Technology Corporation,Beijing 100048,China

1.Introduction

Receding horizon control,also known as model predictive control,originates from process industry in the early 1970s,1and has been successfully applied in different fields such as aerospace engineering,1–8environmental sciences,9chemicalengineering10and robotics.11,12The basic idea of receding horizon control(RHC)is that,an optimal control problem based on current states of a dynamic system is repeatedly solved online over a moving horizon,while only the first sequence of the obtained optimal control laws is implemented as the current control input.Since the time interval of the performance index for the RHC problem is finite,the optimal feedback control law can be determined even for a system which is not open-loop stable.13

In most cases,it is dif ficult to find analytical solutions for RHC problems,especially for time-varying systems.Traditional methods13,14rely on solving the two-point boundary value problem(TPBVP)resulting from the RHC problem by backward sweep of the Riccati differential equation or by transition matrices.It is well-known that these methods are not suitable for online implementation of RHC since they are numerically unstable and time consuming.7,15–18To address the above issue,many numerical methods6,15–18have been proposed.By employing standard numerical integration and quadrature formulas to approximate the state derivatives and the integral cost,Lu15transformed the RHC problem for linear time-varying(LTV)system into a quadratic programming(QP)problem and then obtained approximate closed-form time-varying control laws by solving the resulting QP problem analytically.Yan,16Williams17and Yang et al.6proposed the indirect Legendre pseudospectral method,the indirect Jacobi pseudospectral method,and the indirect Gauss pseudospectral method to solve the RHC problem,respectively.The core idea of the preceding methods was that the corresponding pseudospectral approximations were utilized to transform the TPBVP resulting from the RHC problem into a set of linear algebraic equations.With the variational principle and the generating function,Peng et al.18proposed an ef ficient sparse approach which transforms the resulting TPBVP into a set of sparse symmetric positive de finite linear algebraic equations.As linear algebraic equations could be ef ficiently and accurately solved,both the indirect pseudospectral methods6,16,17and Peng’s approach18were highly effective for online implementation of RHC.

In this paper,motivated by Refs.6,16,17,we propose a novel numerical method called the indirect Radau pseudospectral method to solve the RHC problem in an online manner.The proposed method utilizes the Radau pseudospectral approximation to transform the TPBVP,which results from the RHC problem for LTV system based on calculus of variations and the first-order necessary optimality condition,into wellposed linear algebraic equations.The optimal feedback control law at the current time is then obtained by solving the resulting linear algebraic equations via a matrix partitioning approach.For the nonlinear system,successive linear approximations are obtained through the linearization method or the quasi linearization method.Then all that remains is to solve the resulting linear problems using the similar method for solving the RHC problem for LTV system.Since the collocation points of each pseudospectral approximation are distinguishing,the indirect Radau pseudospectral method(IRPM)and other indirect pseudospectral methods6,16,17employing different pseudospectral approximations transform the resulting TPBVP into linear algebraic equations with different forms and dimensions.Moreover,the boundary conditions of TPBVP are incorporated in different ways in each method.The effectiveness of the proposed method is validated by three examples.The first one is an open-loop unstable LTV system with an analytical model.The second one is the single inverted pendulum which is a nonlinear system.The third one is the space shuttle reentry guidance problem which can be viewed as a trajectory tracking problem for nonlinear system.Simulation results demonstrate that the IRPM can solve the RHC problem online with high accuracy and high computation ef ficiency and the closed-loop systems are stable with the resulting optimal feedback control law.

Recently,the Radau pseudospectral method(RPM),19–22as a direct collocation method for numerically solving optimal control problems,has attracted wide attention.The RPM transforms the optimal control problem into the nonlinear programming problem which is then solved by numerical optimization methodssuch asthesequentialquadratic programming method and the interior point method,whereas the IRPM transforms the TPBVP resulting from the RHC problem into a set of linear algebraic equations which is then solved ef ficiently and accurately by a matrix partitioning approach.The only similarity of the IRPM proposed in this paper and the RPM19–22is that the Radau pseudospectral approximation is employed by both methods to approximate the derivatives of corresponding variables.

2.Problem formulation

2.1.RHC problem for LTV system

Consider a LTV system expressed as

where x∈Rnand u∈Rmare state and control variables,respectively;A(τ)∈ Rn×nand B(τ)∈ Rn×mare continuous coefficient matrices;x0is the initial condition.The system is assumed to be uniformly completely controllable.15

The RHC problem for LTV system at any fixed timet≥ τ0,as described in Refs.15,18,is de fined to be an optimal control problem in which the performance index

is minimized for some chosen δ≤T≤∞ (Tis the horizon length and δ is a positive constant),the nonnegative de finite symmetric weighted matrix Q ∈ Rn×nand the positive de finite symmetric weighted matrix N∈Rm×m,subject to the LTV system dynamics with the initial condition shown as Eq.(1)and the constraint

The goal of RHC for LTV system is to solve the optimal control uoptm(τ)for the above problem at the time interval τ∈[t,t+T]with the current state x(t)as the initial condition,where only the first data uoptm(t)is used as the current control input u(t)to the system,and the rest of uoptm(τ)is discarded.For the next instantaneous timet,the preceding solution process is repeated and the control input is recomputed.According to Ref.23,the control input obtained by such an RHC strategy is given by

where P(t,t+T)∈ Rn×nsatis fies the matrix differential Riccati equation(MDRE)

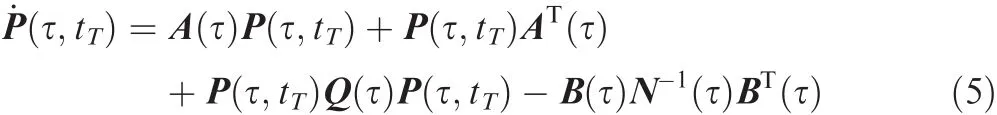
at any time τ∈ [t，t+T]⇐⇒ [t，tT]with the terminal boundary condition

To get the current control input u(t)from Eq.(4),the MDRE shown as Eq.(5)needs to be integrated backward fromt+Ttotfor every current timetwith the boundary condition shown as Eq.(6).As noted above,online integration of the MDRE for everyt≥ τ0is a time-consuming work and may pose numerical unstability.Therefore,to avoid the integration of MDRE and improve the ef ficiency in real-time computation of RHC for LTV system,the IRPM is developed to transform the above problem into linear algebraic equations which can be ef ficiently and accurately solved online.

2.2.RHC problem for nonlinear system

Considera nonlinearsystem with theinitialcondition expressed as

where f is a function vector in which all elements are continuous and differentiable.The RHC problem for nonlinear system at any fixed timet≥ τ0,as described in Ref.17,is de fined to find the optimal control uoptm(τ)that minimizes the performance index

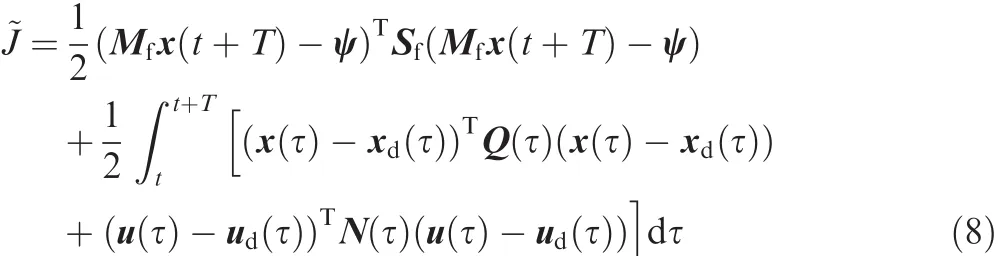
subject to the nonlinear system dynamics and the initial condition shown as Eq.(7),where xd∈Rnand ud∈Rmare desired time-varying state and control variables,respectively;Sf∈ Rn×nis the nonnegative de finite symmetric weighted matrix;ψ∈Rnis the desired vector of values for linear combination of desired final state variable Mfx(t+T)and Mf∈ Rn×nis a given matrix.

As same as the goal of RHC for LTV system mentioned in Section 2.1,the nonlinear optimal control problem de fined by Eqs.(7)and(8)is solved repeatedly as time goes on,while the obtained optimal control input is only applied at the current time.

3.Indirect Radau pseudospectral method

3.1.Method for solving RHC problem for LTV system

Based on calculus of variations and the first-order necessary optimality condition,the solution of the RHC problem for LTV system should satisfy thefollowing Hamiltonian canonical equation18:

To compute the optimal control uoptm,the Hamiltonian canonical equation shown as Eq.(9)needs to be solved first.The Hamiltonian canonical equation can be expressed in the form of state space as

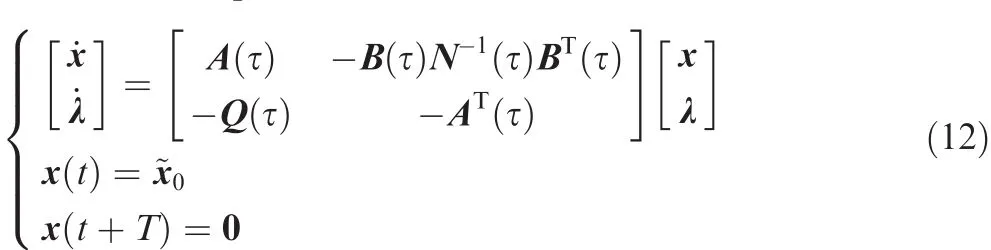
which is the TPBVP.The IRPM is proposed to solve the above TPBVP with the detailed description given as follows.

The state and costate variables are discretized at the end point=1 andNLegendre–Gauss–Radau(LGR)points（k=1，2，...，N）distributed on the interval[-1,1).NLGR points including the initial point=-1 are de fined as the roots of the polynomialPN）+PN-1，where

is theNth degree Legendre orthogonal polynomial.Since the discrete points lie in the interval[-1,1],the TPBVP shown as Eq.(12)is transformed to this interval by the following linear transformation for time

It follows that the TPBVP shown as Eq.(12)can be replaced by

The state and costate variables are approximated asNth degree polynomials through Lagrange interpolation as

areNth degree Lagrange interpolation basis functions;areN+1 interpolation points which are equal to theN+1 discrete points.

whereDkjshown as Eq.(22)are elements of the differential matrix D∈RN×(N+1).

The dynamic equations shown as Eq.(15)are discretized by imposing the condition that the derivatives of state and costate approximations expressed as Eqs.(20)and(21)satisfy the differential equation exactly at the LGR points.

Thus,by substituting Eqs.(20)and(21)into Eq.(15)and collocating atNLGR points，Eq.(15)is transformed into the following algebraic equations:

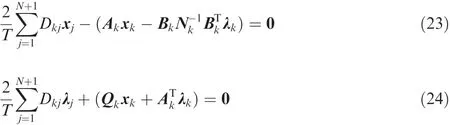
where for a generic matrix X（~τ）,the notation Xkdenotes X），（X=A，B，N，Q，λ，x）.Rewriting Eqs.(23)and(24)in block matrix notation,the following equation is obtained:

well-posed linear algebraic equations expressed as Eq.(27)is solved for obtaining Zeas

It is obvious that if the current state variable~x0is known,state,control and costate variables at the discrete points can be solved from Eqs.(30)and(31),and the values of variables at instants of time between the discrete points can be obtained by interpolation.It should be noted that the preceding optimal control law is obtained without any complex and timeconsuming computation.

3.2.Method for solving RHC problem for nonlinear system

To solve the RHC problem for nonlinear system,the linearization method or the quasi linearization method is employed to transform the preceding nonlinear optimal control problem,as described in Section 2.2,into a sequence of linear optimal control problems first.

In the linearization method,the performance index shown as Eq.(8)is expanded up to second order and the system dynamics as shown in Eq.(7)are expanded up to first order with higher order terms neglected around the desired trajectory(xd,ud).The original problem is transformed into the following linear optimal control problem.

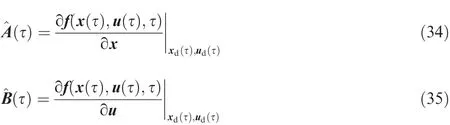
In the quasi linearization method,the performance index is expanded up to second order and the system dynamics are expanded up to first order around the nominal trajectory.The original problem is transformed into the following linear optimal control problem.

Problem 1 can be regarded as the special case of Problem 2 with the higher order terms of the system dynamics for the linearization of the nonlinear system neglected and the nominal trajectory fixed to the desired trajectory.In view of generality,the following derivation process is based on Problem 2.

The Hamiltonian function for Problem 2 is expressed as

As before,the IRPM is proposed to transform the above TPBVP into linear algebraic equations.Since the processes of discretizing and collocating are similar to that in Section 3.1,the details are not described.Here,the results transformed from the dynamics equations in Eq.(45)fork=1,2,...,Nare given by

The procedure for implementing the RHC for nonlinear problem similar to that in Ref.17is summarized as follows:

Step 1.For the given horizon lengthTand the desired trajectory(xd,ud),guess a nominal trajectory for the interval τ∈ [t,t+T]and apply the quasi linearization method to the RHC problem for nonlinear system.A suitable guess would be the desired trajectory.

Step 2.Solve the sequence of TPBVPs:

(a)Solve the linear equations Eq.(52).

(b)Update the nominal trajectory using Eqs.(55)and(56).

(c)Repeat steps(a)and(b)using the solution from the previous iteration as initial guess until the 2-norm of the change in state variable ‖-x‖ is within a prescribed tolerance ε or a giv iteration number is exceeded.

Step 3.Apply the optimal control input at the current time which is obtained from the converged trajectory from Step.2 to the nonlinear system,and repeatSteps1and2untilτ= τf(τfistheendtime).

As mentioned above,as the quasi linearization method is employed,in order to get the optimal control at any instantaneous timet≥ τ0，the resulting TPBVPs need to solved repeatedly at the current time until the state deviations between the current iteration and the previous iteration are within a prescribed tolerance or a given iteration number is exceeded.However,as the linearization method is employed,the resulting TPBVP only needs to be solved once at the current time.

4.Applications

4.1.LTV system with an analytical model

The following two-dimension LTV system with an analytical model is considered:15

with the performance index and the terminal constraint shown as Eqs.(2)and(3),respectively.The preceding system is an open-loop unstable system,but it is controllable for all τ≥ 0.

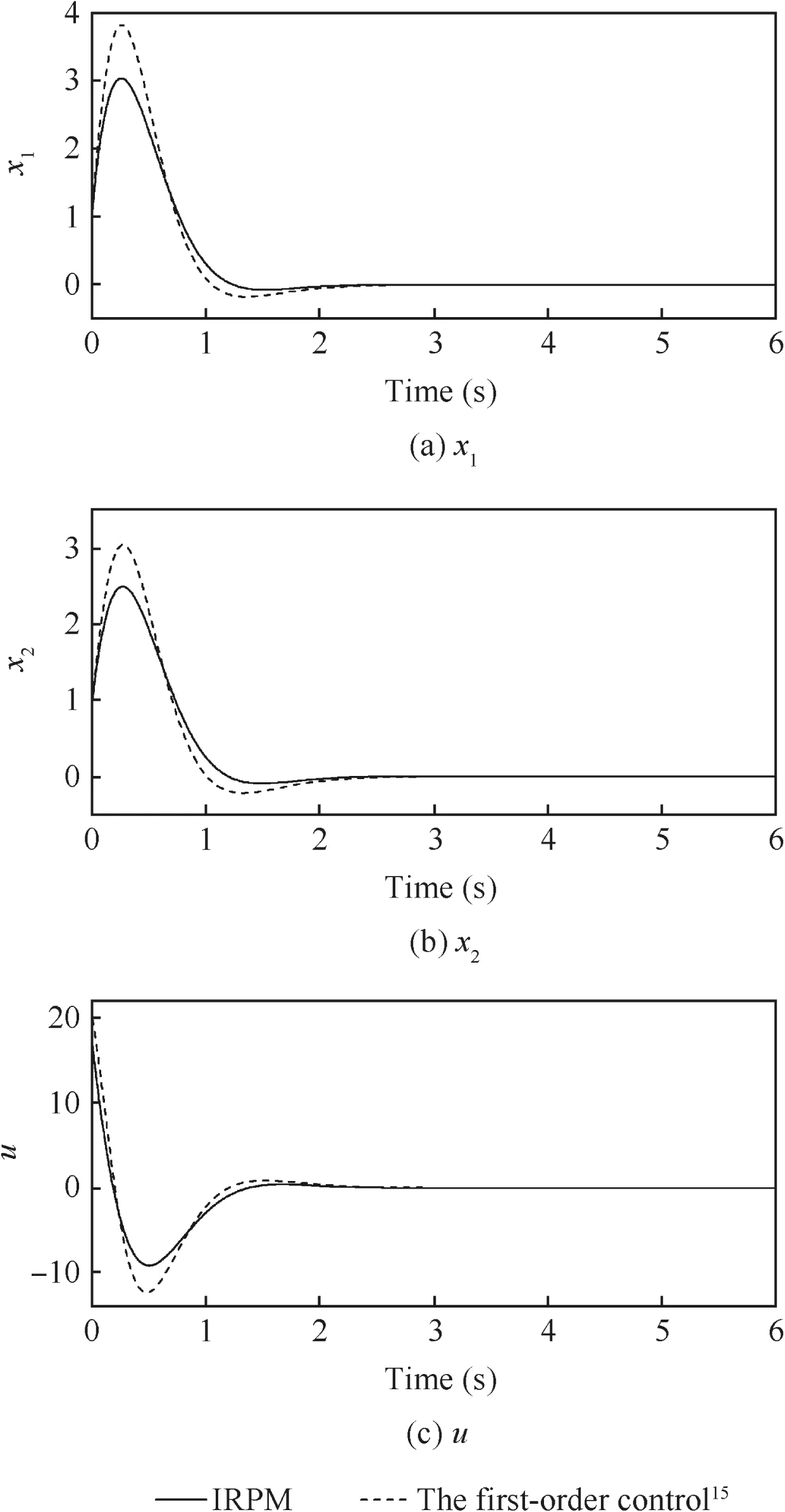
Fig.1 Comparison between results of IRPM and the first-order control law.15

With the initial condition x0=[1,1]T,the weight matrices Q=diag{1,1}and N=1,the simulation step 0.01 s,the LGR points’numberN=2,and the horizon lengthT=0.6 s，the preceding RHC problem is solved using the method proposed in Section 3.1.The results are shown in Fig.1 alongside the results obtained from the first-order control law derived in Ref.15.As the first-order control law is derived based on the subintervalnumber=2andthesubintervallengthh=0.3 s,the horizon lengthT==0.6 s equals that was used in the IRPM.The responses as shown in Fig.1 clearly demonstrate that the closed-loop system is stable in both cases,while the results of the IRPM have a smaller control input peak value and a smaller overshoot.Thus,with the same horizon length and the same subinterval number,the IRPM has a better performance than the first-order control law.15

Next,simulations are made with various LGR points’numbers and horizon lengths to learn more about the effects on the results.

The computation time for the optimal control input at the current time in all cases are shown in Table 1.It is observed that all the maximum computation timetcal_maxand the average computation timetcal_aveare much shorter than the speci fied simulation step 0.01 s,demonstrating high computation ef ficiency of the proposed method.Two key related features are also seen from Table 1.First,as the LGR points’numberNincreaseswhilethehorizonlengthis fixed,theaveragecomputation timetcal_aveincreases.Second,as the horizon length increases while the LGR points’numberNis fixed,there are little differences between the average computation timetcal_avein all cases.This is because that the most time-consuming work in the IRPM is the inverse of Veas shown in Eq.(28),and increasing the LGR points’number leads to increase of the dimension of Vewhich results in a longer average computation time,while increasing the horizon length has no effect on the dimension of Ve.

Table 1 Computation time in all cases.

Fig.2(a)–2(c)give the results for the LGR points’numberN=2 toN=10 by steps of 2 with the horizon lengthT=0.6 s.It is observed that there are only small differences between the results for cases of different LGR points’numbers with the same horizon length.Regarding the result forN=10 as the reference,it can be seen that state and control curves of other cases converge to the reference curves(x1_ref,x2_ref,uref)with great rapidity.The maximum absolute errors between the reference result and another result are de fined as

The values ofex1，ex2，euare shown in Fig.2(d).It can be seen that all errors decrease nearly over a linear trend untilN=8,demonstrating the spectral convergence rate of the Radau pseudospectral approximation.

Fig.3 gives the results for horizon lengthT=0.3 s toT=1.5 s by steps of 0.3 s with LGR points’numberN=2.It is observed that there are large differences between the results for cases of different horizon lengths with the same LGR points’number.For smaller horizon length which can be viewed as achieving the control objective in a faster way,the control input peak value and the overshoot are larger while the stabilization time is shorter.

Thus,it can be concluded that the computation ef ficiency of the optimal control law depends on the LGR points’number,

Fig.2 Comparisons between results for cases of different LGR points’numbers with horizon length T=0.6 s.

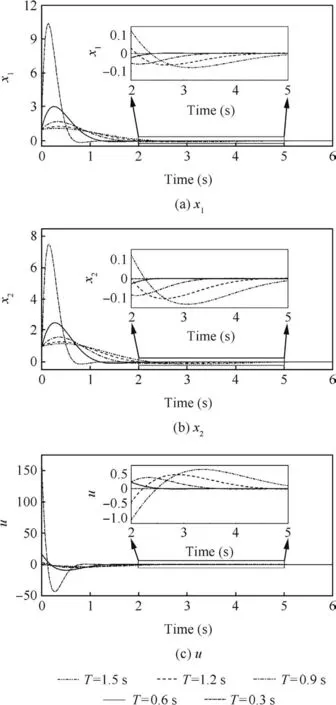
Fig.3 Comparisons between results for cases of different horizon length with LGR points’number N=2.

while the gains of the optimal control law are mainly affected by the horizon length.

4.2.Single inverted pendulum

The single inverted pendulum depicted in Fig.4 is a complex,nonlinear,coupling,and open-loop unstable system with equations of motion expressed as follows:

Fig.4 Single inverted pendulum.

whereM=0.5 kg andm=0.2 kg are mass of the driving cart and the pole,respectively;xis the position of the driving cart;l=0.3 m is the length of the pole;φ is the inclined angle between the pole and the vertical upward direction measured counterclockwise for the vertical upward direction;Fis the traction on the driving cart which is the control variableuof the inverted pendulum;I=ml2/3 is the rotational inertia of the pole;b1=0.001 N ·m ·s/rad is the friction coef ficient between the pole and the driving cart;b2=0.1 N·s/m is the friction coef ficient between the driving cart and the horizontal plane.The performance index is shown as Eq.(8).

Fig.5 gives the results of the linearization method and the quasi linearization method with the tolerance ε=1 × 10-6and the maximum iteration numbern=3.Eφ，E˙φ，Ex，E˙xandEuin Fig.5 denote the errors for corresponding variables between the results of the linearization method and the results of the quasi linearization method.It can be seen that there are small differences between the results of both methods and errors of the results converge to 0 rapidly.Both of the methods have achieved the control objective and both of the results demonstratetheclosed-loop stability ofcontrolling the preceding system using the IRPM.

Since the RHC problem for nonlinear system is approximated with successive linear approximations via the linearization method or the quasi linearization method,the effects caused by the LGR points’number and the horizon length on the results would be similar to that of the RHC problem for LTV system.Simulations are made with various maximum iteration numbers and tolerances to further study the effects on the results with the quasi linearization method.Results show that the control objective has been achieved in all simulation cases.

First,results of cases for various tolerances without limit of maximum iteration number are compared.We choose the result of the case ε=1 × 10-10as the reference result.The errors of the performance index,state variables,costate variables,and control variables between the reference result and the result of another case are de fined as

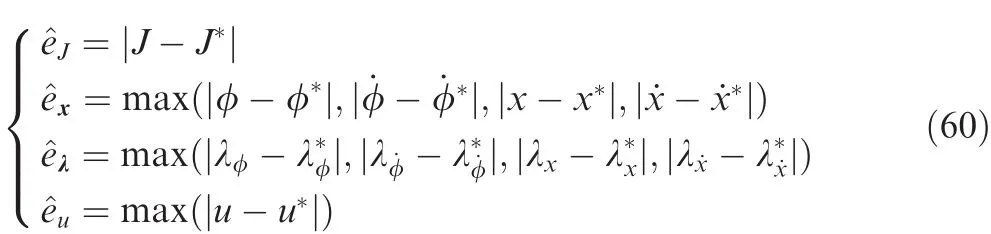
where the symbol*represents the reference result.Table 2 shows the errors of cases for various tolerances.It is observed that the errors of all cases are very small and results are closer to the reference result as the tolerance ε decreases.It is worth noticing that with the prescribed tolerance,more iteration numbers are needed at the beginning of the simulation while iteration numbers decrease as time goes on.Table 2 demonstrates the high accuracy of the IPRM.

Fig.5 Comparison between results of linearization method and quasi linearization method.

Then,results of cases for various maximum iteration numbers without limit of tolerance are compared.The errors are de fined as

where the symbolkrepresents the result of maximum iteration numbern=k.Table 3 shows the errors of the cases for various maximum iteration numbers.It is observed that the errors decrease fast as the maximum iteration number increases before the maximum iteration number reaches 7,and then the errors remain relatively unchanged.Table 3 demonstrates the fast convergence speed of the IRPM.

It is evident that both the decrease of the tolerance and the increase of maximum iteration number require more computation time when using the quasi linearization method.Thus,we should properly choose the tolerance and the maximum itera-

Table 2 Errors between reference results and results of other cases with various tolerances.

Table 3 Errors between result of maximum iteration number n=k and results of maximum iteration number n=k-1.

tion number to ensure the computation ef ficiency and meet the requirement of accuracy at the same time.

4.3.Space shuttle reentry guidance

The space shuttle reentry guidance problem3,7is considered in this section.The equations of translational motion for the space shuttle over a spherical,non-rotating earth are given by3,7

wherer,θ,φ,V,γ and ψ are radial distance,longitude,latitude,velocity, flight-path angle and heading angle,respectively;m1=92709 kg is the mass of the space shuttle;g=μ/r2isthe gravity acceleration and μ=3.9805×1014m3/s2is the geocentric gravitational constant;σ is the bank angle;LandDare lift force and drag force,respectively,and are expressed as

whereS=249.9092 m2is the reference area;q=0.5ρV2is the dynamic pressure;ρ is the atmosphere density and is based on the exponential model ρ = ρ0e-（r-R0）/H; ρ0=1.225 kg/m3is the sea level atmosphere density;R0=6371004 m is the earth radius;H=7254.24 m is the density scale height;the lift coef ficientCLand the drag coef ficientCDare given as

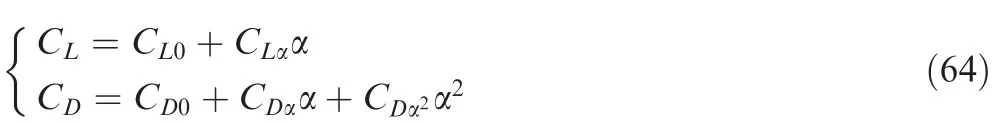
whereCL0=-0.207,CLα=1.6756,CD0=0.0785,CDα=-0.3529,CDα2=2.04, α is the angle of attack measured in radians.The angle of attack α and the bank angle σ are the trajectory control inputs.

Thepath constraintsconsisting oftheheating rate constraint,the dynamic pressure constraint and the total load constraint are expressed as

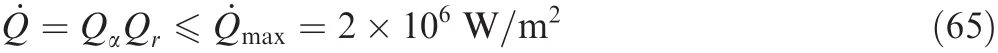
The initial state constraints areh0=79250 m，θ0=0°,φ0=0°,V0=7800 m/s，γ0=-1°and ψ0=90°,and the terminal state constraints arehf=24380 m,θf=80°, φf=30°,Vf=762 m/s and γf=-5°.

The desired trajectory is generated using the open source software GPOPS.24In GPOPS,the Radau pseudospectral method19–22is employed to discretize the trajectory optimization problem and the resulting nonlinear programming problem is solved by the limit version of the software SNOPT.25The LGR points’number isN=100 and the object function expressed as follows is to minimize the maximum heating rate of the whole trajectory

The time histories of the desired trajectory,the corresponding trajectory control inputs and the path constraints are shown in Figs.6 and 7 by solid lines,where it can be seen that all constraints are satis fied.The flight time is 2047.59 s and the maximum heating rate of the whole trajectory is 7.6452×105W/m2.

With the desired trajectory and subject to the nonlinear equations of motion shown as Eq.(62),the space shuttle reentry guidance problem,which is regarded as a trajectory tracking problem,can be formulated as an RHC problem for nonlinear system and is solved through the proposed method in Section 3.2.The approximation method used in this example is the linearization method.The nonzero elements of the Jacobian matrices（τ）∈ R6×6and（τ）∈ R6×3in Eq.(33)can be analytically expressed as=sinγ，=Vcosγ，on the time-varying desired trajectory so that the Jacobian matrices are pure functions of time.

Fig.6 Time histories of state variables and control variables.

In the closed-loop guidance simulation,both the simulation step and the guidance cycle are set as 1s and the weight matricesare valued asQ=diag 7 × 10-7，1.3 × 106，5.8 × 105，2.5×10-3，1.5×105，1.5×105，N=diag{130,8},Sf=0 with the horizon lengthT=200s and the LGR points’number for the IRPMN=20.Two test cases with the initial state deviations set as Δh0=600m， Δθ0=0.05°, Δφ0=0.05°,ΔV0=20m/s，Δγ0=0.1°, Δψ0=0.1° forcase1 and Δh0=-600m， Δθ0=-0.05°, Δφ0=-0.05°, ΔV0=-20m/s，Δγ0=-0.1°,Δψ0=-0.1°for case 2 are simulated.

Table 4 shows the computation time for the optimal guidance law and the errors of terminal states between the closed-loop trajectories and the desired trajectory.It is observed that the maximum computation timetcal_maxand the average computation timetcal_avefor two cases are much shorter than the simulation step and the guidance cycle,which demonstrates that the optimal guidance law is obtained by the proposed IRPM with high computation ef ficiency.Fig.6 gives the results of the closed-loop trajectories,the corresponding control inputs and their errors relative to the desired ones.Eh，Eθ，Eφ，EV，Eγ，Eψ，EαandEσin Fig.6 denote the errors for corresponding variables between the results of the closedloop trajectories and the results of the desired trajectory.It is observed that the closed-loop trajectory can track the desired trajectory with small terminal state errors in the presence of a rational range of initial state deviations.Fig.7 shows the curves of path constraints of the closed-loop trajectories,where it can be seen that all path constraints are satis fied when the guidance law is applied.From the simulation results,it can be concluded that the IRPM is effective to deal with the space shuttle reentry guidance problem.

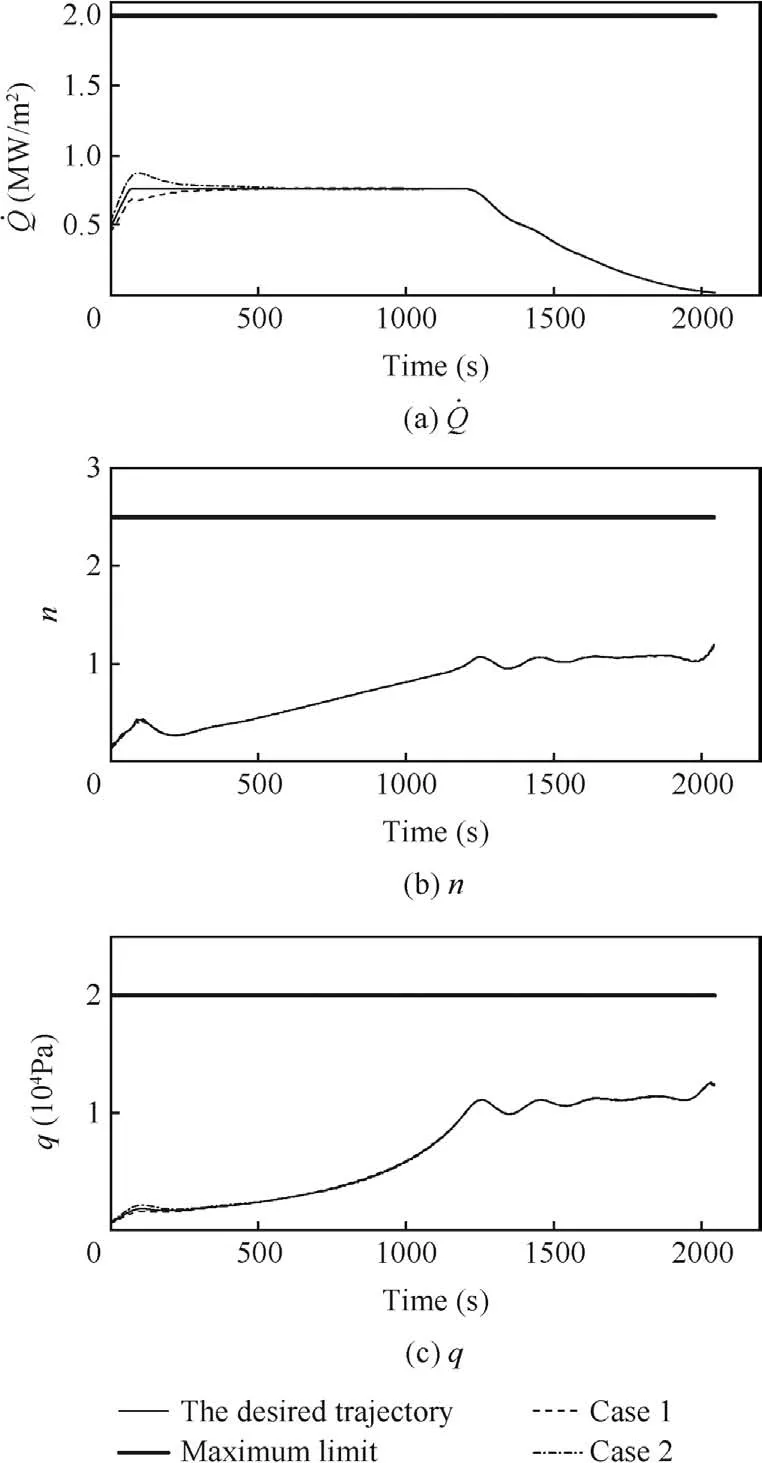
Fig.7 Time histories of path constraints.

Table 4 Computation time for optimal guidance law and errors of terminal states between closed-loop trajectories and desired trajectory.

5.Conclusions

(1)Using the IRPM,the TPBVP resulting from the RHC problem is discretized into well-posed linear algebraic equations which is solved ef ficiently and accurately via a matrix partitioning approach. Since complex computations such as backward sweep of the Riccati differential equation and transition matrices are avoided,the numerical stability and the high computation ef ficiency can be guaranteed.

(2)As the Radau pseudospectral approximation,employed in the IRPM,has an exponential convergence rate for smooth problems,highly accurate optimal solutions can be obtained via a small number of LGR points,which in turn can save computer memory storages and improve computation ef ficiency.

High computation ef ficiency and high accuracy of the IRPM and stability of the closed-loop systems with the resulting optimal feedback control law are validated through three numerical examples.Future work will concentrate on the application of the proposed method to other practical aerospace problems such as formation and station keeping of spacecraft,nanosatellite fast deorbit using electrodynamic tether,etc.

This work was supported by the National Natural Science Foundation of China(Nos.61174221 and 61402039).

1.Zhang XY,Duan HB,Yu YX.Receding horizon control for multi-UAVs close formation control based on differential evolution.Sci China Inf Sci2010;53(2):223–35.

2.Zhang LM,Sun MW,Chen ZQ,Wang ZH,Wang YK.Receding horizon trajectory optimization with terminal impact speci fications.Math Prob Eng2014;604705-1-8.

3.Cai WW,Zhu YW,Yang LP,Zhang YW.Optimal guidance for hypersonic reentry using inversion and receding horizon control.IET Control Theory Appl2015;9(9):1347–55.

4.Williams P.Spacecraft rendezvous on small relative inclination orbits using tethers.J Spacecraft Rockets2005;42(6):1047–60.

5.Lu P.Regulation about time-varying trajectories:precision entry guidance illustrated.J Guid Control Dyn1999;22(6):784–90.

6.Yang L,Zhou H,Chen WC.Application of linear Gauss pseudospectral method in model predictive control.Acta Astronaut2014;96:175–87.

7.Tian BL,Zong Q.Optimal guidance for reentry vehicles based on indirect Legendre pseudospectral method.Acta Astronaut2011;68(7–8):1176–84.

8.Peng HJ,Gao Q,Wu ZG,Zhong WX.Optimal guidance based on receding horizon control for low-thrust transfer to libration point orbits.Adv Space Res2013;51(11):2093–111.

9.Park Y,Harmon CT.Autonomous real-time adaptive management of soil salinity using a receding horizon control algorithm:a pilot-scale demonstration.J Environ Manage2011;92(10):2619–27.

10.Zavala VM,Biegler LT.Optimization-based strategies for the operation of low-density polyethylene tubular reactors:Nonlinear model predictive control.Comput Chem Eng2009;33(10):1735–46.

11.Du Toit NE,Burdick JW.Robot motion planning in dynamics,uncertain environments.IEEE Trans Rob2012;28(1):101–15.

12.Lee SM,Kim H,Myung H,Yao X.Cooperative coevolutionary algorithm-based model predictive control guaranteeing stability of multi-robot formation.IEEE Trans Control Syst Technol2015;23(1):37–51.

13.Ohtsuka T,Fujii HA.Real-time optimization algorithm for nonlinear receding-horizon control.Automatica1997;33(6):1147–54.

14.Bryson AE.Dynamic optimization.Menlo Park,CA:Addison-Wesley;1999.p.315–8.

15.Lu P.Closed-form control laws for linear time-varying systems.IEEE Trans Autom Control2000;45(3):537–42.

16.Yan H,Fahroo F,Ross IM.Optimal feedback control laws by Legendre pseudospectral approximations.Proceedings of the American control conference;2001 June 25–27;Arlington,VA.Piscataway(NJ),IEEE Press;2001.p.2388–93.

17.Williams P.Applications of pseudospectral methods for receding horizon control.J Guid Control Dyn2004;27(2):310–4.

18.Peng HJ,Gao Q,Wu ZG,Zhong WX.Ef ficient sparse approach for solving receding-horizon control problems.J Guid Control Dyn2013;36(6):1864–72.

19.Garg D,Patterson MA,Francolin C,Darby CL,Huntington GT,Hager WW,et al.Direct trajectory optimization and costate estimation of finite-horizon and in finite-horizon optimal control problems using a Radau pseudospectral method.Comput Optim Appl2009;49(2):335–58.

20.Garg D,Hager WW,Rao AV.Pseudospectral methods for solving in finite-horizon optimal control problems.Automatica2011;47(6):829–37.

21.Fahroo F,Ross IM.Pseudospectral methods for in finite-horizon optimal control problems.J Guid Control Dyn2008;31(4):927–36.

22.Kameswaran S,Biegler LT.Convergence rates for direct transcription of optimal control problems using collocation at Radau points.Comput Optim Appl2007;41(1):81–126.

23.Kwon WH,Pearson AE.A modi fied quadratic cost problem and feedback stabilization of a linear system.IEEE Trans Autom Control1977;22(5):838–42.

24.Rao AV,Benson DA,Darby CL,Mahon B,Francolin C,Patterson M,et al.User’s manual for GPOPS version 4.x:A matlab software for solving multiple-phase optimal control problems using hp-adaptive pseudospectral methods.[Internet].[cited 2011 August].Available from:http://www.gpops2.com/usersManual/usersManual.html.

25.Gill PE,Murray W,Saunders MA.SNOPT:An SQP algorithm for large-scale constrained optimization.SIAM Rev2002;47(1):99–131.