Plastic wrinkling prediction in thin-walled part forming process:A review

Liu Nan,Yang He,Li Heng,Yan Siliang

State Key Laboratory of Solidi fication Processing,School of Materials Science and Engineering,Northwestern Polytechnical University,Xi’an 710072,China

1.Introduction

Lightweight thin-walled parts have attracted more and more applications in various industrial sectors such as aviation,aerospace and automobile.The wrinkling induced by the compressive instability is one of the major defects in thin-walled part forming processes.Wrinkling may be a serious obstacle to implementing the forming process and assembling the parts,and may also play a signi ficant role in the wear of the tool.In order to improve the productivity and quality of products,the wrinkling problem must be solved.1–3However,the initiation of wrinkles are interactively affected by many factors such as stress state,mechanical properties of the material,geometry of the workpiece,and especially contact conditions(boundary condition).It is dif ficult to analyze the wrinkling initiation and growth considering all the factors because the effects of the factors are very complicated and the wrinkling behavior may show a wide scatter of data for a small deviation of factors4,5(see Fig.1).

Nowadays,the trend towards designing very light-weight thin-walled structures requires that forming process involves complicated boundary conditions(CBC).The characteristics of the CBC are multiple tooling constraints,complex loading paths and history,complicated contact conditions caused by dynamic die constraints which are changing in time and space and perturbation of clearances between workpiece and dies.1It is known that the boundary conditions play vital roles in restraining wrinkling in thin-walled part forming processes.Consequently,the predication of wrinkling in thin-walled part forming is further complicated,which is attributed to the fact that the boundary condition during the accurate forming process is changing in time and space and the contact nonlinearities make the bifurcation check more challenging.Taking in-plane roll-bending of strip(IRS)6,7as an example,if deformation condition is inappropriate,it results in multiple instability modes including external wrinkling,internal wrinkling,turning-I,and turning-II.8The tube bending process,based on a CNC rotary draw bending(RDB)method,9is also a typical forming process with complicated boundary conditions.There are five complicated contact interfaces(multidies)altogether in the tube bending progress:tube-wiper die,tube-mandrel,tube-bend die,tube-pressure die and tubeclamp die.If deformation condition is inappropriate,it results in multiform and asymmetric local distributed wrinkles on the surface of the tube.10,11

Motivated by these challenges,much effort has been undertaken by industrial and academic researchers aimed at accurately predicting the wrinkling in thin-walled parts forming processes.However,accurate prediction of wrinkling instability is still one challenge and a focused issue in thin-walled part forming processes,especially involving CBC.The prediction methods for the onset of wrinkling can be broadly divided into six categories:the static equilibrium method,the energy method,initial imperfection method,the eigenvalue buckling analysis method,the static-implicit finite element method and the dynamic-explicit finite element method.However,all the methods mentioned above have their own intrinsic limitation to predicted wrinkling under CBC.

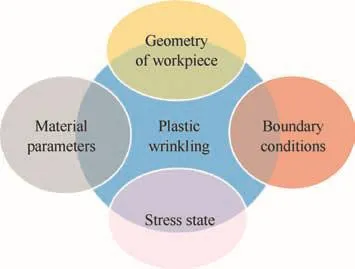
Fig.1 Plastic wrinkling is interactively affected by stress state,materialparameters,geometry ofworkpiece and contact conditions.

In this paper,a review of current prediction methods is assessed in terms of their advantages and limitations.By using a combination of explicit FE method,initial imperfection and energy conservation,a hybrid method is recommended to predict plastic wrinkling in thin-walled part forming.The trend towards designing very light-weight thin-walled structures requires that forming process involves multi-dies constrains,the perturbation of clearances between workpiece and dies and the contact conditions changing in time and space.Therefore,considering urgent demands for solving the problem of plastic wrinkling prediction under complicated boundary condition,the trends and challenges of prediction methods in thin-walled part plastic forming are presented.

2.Analytical approach

Mass and great efforts have been taken in sheet metal wrinkling research using analytical approach for more than half a century.It is known that the wrinkling defects during thinwalled part forming processes can be simpli fied as the buckling stability of thin plate or shell under laterally constrained conditions.For example,the tube in rotary draw bending and the cylinder in spinning forming can be simpli fied to a shell model.Stamping of sheet and in-plane roll-bending of strip can be simpli fied into a thin plate model.The analytical approach is mainly based on the static equilibrium method,the energy method and initial geometric imperfection method.A comprehensive comparison of the characteristics of the above three methods are shown as follows.

2.1.Static equilibrium method

In the static equilibrium method,for a thin plate undergoing the uniform stress field of in-plane compressive loading,Px,in thex-direction,Py,in they-direction andPxy,inx–yplane,assuming that these stresses are parallel to the mid-plane and all the stress states that through the thickness is uniform before buckling(see Fig.2).In Fig.2,Wis the width of the plate andLthe length of the plate.

Fig.2 A rectangular thin plate under in-plane compressive loading.

In rectangular coordinate system,when the sheet undergoes small de flection bending,the partial differential equilibrium equation(elastic buckling instable problem)is given as follows:

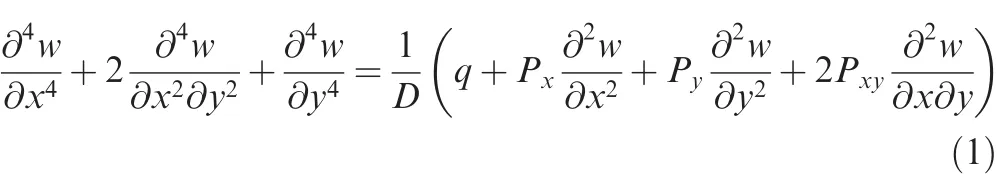
wherewis the de flection function,qthe normal concentrated load,andDthe bending stiffness.

Using equations of boundary conditions of the four sides,the partial differential equilibrium equation can be solved.After that,the critical value of the compressive stress and de flection function are obtained.Liang and Hu12studied a square plate under compression in one direction and found that the critical stress differed greatly with different boundary constraints.

Unlike the sheet model,a shell model possesses initial curvature κxand κy.The partial differential equilibrium equation of a shell with small de flection is deduced as follows,which is an eight-order partial differential equations:

whereEis the elastic modulus andtthe thickness of the plate.

Wang et al.13presented a weighted solution for the critical load of a cylindrical shell.The buckling of an axisymmetric cylindrical shell with simple-support and clamped end conditions was studied as examples.In fluence factors of the critical load are found from the differential equations and in fluence coef ficients are determined.Peek14solved the problem of a tube under pure bending as a generalized plane strain problem and the onset of wrinkling is predicted by introducing buckling modes involving a sinusoidal variation of the displacements along the length of the tube.

Therefore,according to the differential equilibrium equations of plate or shell,the critical buckling load of a structure under the corresponding boundary and load conditions are obtained.The main advantages of the static equilibrium method are:it can provide a global view in terms of the general tendency and the effect of individual parameters on the onset of wrinkling.

However,when the boundary conditions are complicated,or structures have irregular geometrical shape,or distributions of stress are uneven,etc.,it is dif ficult to solve such problems.It makes Eqs.(1)or(2)become a partial differential equation with variable coef ficients,which is unable to get the analytical solution.

On the other hand,in the process of solving the partial differential equilibrium equation,the pre-buckling stress state in the plate examined for wrinkling is assumed in membrane state,and thus,the shear strains and stresses are ignored.All the formulations are developed within the context of thin plate and shell theory,therefore,the thickness of the sheet and all the stress states through the thickness are assumed to be uniform before buckling.Therefore,past static equilibrium method has been concentrated on some relatively simple compressive instability problems with less complex geometry and boundary conditions.

2.2.Energy method

Theenergy method hasbeen extensively employed in Timoshenko and Gere15to study the elastic buckling of thin plates and shells with various boundary conditions.In his solution,a de flection form may be assumed for the plate and the critical buckling condition can be assessed by equating the internal energy of the buckled plate,ΔU,and the work done by the in-plane membrane forces,ΔT.If the internal energy for every possible assumed de flection is larger than the work produced by membrane forces,the sheet is under a stable equilibrium condition.Hence,the critical moment of wrinkling is obtained when potential energy remains unchanged.That is,

By appropriately choosing the defection form to re flect the boundary restriction and equating the energy,ΔT=ΔU,the critical buckling stress can be calculated analytically as a function of stress,material properties and geometry parameters.

Therefore,energy method has been another approach to analytically investigate the wrinkling problem such as flange wrinkling in Senior,16Morovvati et al.,17Shafaat et al.,18Yu and Johnson,19Kowsarinia et al.,20Cao and Wang,21,22and membranes wrinkling in Wong and Pellegrino.23

The major advantage of the energy method is that it avoids solving the partial differential equilibrium equations.It only considers the beginning and the end of the deformation(the deformation energy ΔUand the work force ΔT).Therefore,this method can deal with some more complex boundary conditions of forming problems.

For more complicated geometry and boundary conditions,Finite element method(FEM)can sometimes assist in developing analytical models.Using a combination of implicit finite element analysis and energy conservation,Cao et al.24,25proposed a new criterion for wrinkling in sheet forming process.Adopting this energy criterion,Cao extensively studied wrinkling in various forming processes such as the conical cup deep drawing,square cup deep drawing,and Yoshida buckling test.Cao et al.26carried out a new buckling test(Contact Buckling Test)on characters of the contact of tooling with or without one-side contact.Different buckling phenomena such as oil canning,buckling at the loading stage and buckling at unloading were observed and explained through a stress-based wrinkling predictor.

An analytical energy-based model combined with explicit algorithm was first proposed by Li Heng to predict the wrinkling occurring in rotary-draw-bending process of a thinwalled tube9,27,28and rectangular tube.29From the global viewpoint,the effects of the basic parameters including the geometrical,material and clearance and friction on the onset of wrinkling are clari fied in terms of energy and each parameter has their own speci fic physical meaning in the thin-walled tube bending process.

However,both the works of Li Heng and Cao Jian are based on the same assumptions as follows:(1)the thickness of the sheet or shell is assumed to be uniform;(2)the pre-buckling stress state in the sheet or shell is assumed to be in membrane state;(3)the stress state through the thickness is assumed to be uniform before buckling;(4)the effective dimensions undergoing compressive stress should be inerratic.Since the above assumptions still have some discrepancy compared with the actual forming condition(complicated friction and clearance cannot be taken as a consideration in the energy methods),the energy method may not suitable to the forming process,which have complicated geometry or contact interfaces between workpiece and dies.It is this dif ficulty that limits the effectiveness of the energy method.

2.3.Initial imperfection method

Based on the assumptions of simple supports and a membrane state of pre-buckling stress distribution,Timoshenko and Gere15indicated that real cylinders buckle at loads much lower than the classical buckling load.Experimental buckling loads as low as 30%of the classical load are not uncommon.The search for reasons responsible for this discrepancy led to an enormous amount of research in the subsequent decades.The dominant factor contributing to the discrepancy between theory and experiment for axially compressed cylinders is initial geometric imperfections.An enormous amount of research has therefore been carried out on the imperfection sensitivity of shell buckling.The most notable contributors in this research are Donnell and Wan,30Peek and Hilberink,31Kyriakides and Corona,32and Hutchinson and He.33

By considering initial imperfection,the partial differential equilibrium equation of a cylindrical shell is deduced as follows(κx=0, κy=1/R,whereRis the radius of the tube andLthe length of the tube):

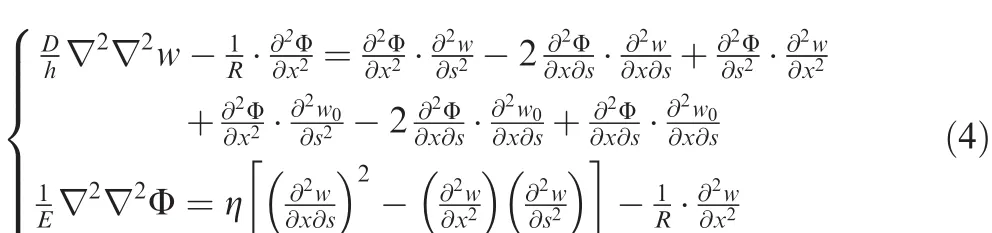
where Φ is stress function,xthe axial direction,sthe circumferential direction,hthe thickness of the shell,and η the factor of initial imperfection.The de flection functionwis described as

wherea,b,c,d,a0are constant.

However,in an analytical approach whether static equilibrium method or the energy method considering initial imperfection,simpli fications and assumptions are still made in the material model,geometry or boundary conditions,and therefore the method is quite limited in terms of applicability and reliability.There are two main dif ficulties encountered in initial imperfection method in the previous decades.First,the buckling phenomenon in shells is a highly complex one,described by nonlinear partial differential equations too dif ficult to solve except for a few simple cases.Second,the buckling of the thin-walled structure is generally sensitive to real geometric imperfections induced in the fabrication process,while the assumed imperfection is based on idealized.

3.Finite element method

Theincreased computation capability makesnumerical method a prime tool to solve the wrinkling instability problems.There are three types of numerical procedures that can be used to solve bifurcation problems:(1)eigenvalue buckling analysis;(2)static-implicit finite element method;(3)dynamicexplicit finite element method.Understanding the nature,advantages and disadvantages of these algorithms is very helpful for choosing the right algorithm for a particular problem.

3.1.Eigenvalue buckling analysis

The essence of eigenvalue buckling analysis is seeking for singular points of a structure stiffness matrix under a linear perturbation.Critical load and buckling modes are obtained by extracting the eigenvalue and eigenvectors from Eq.(7).34

In Eq.(7),Keis the elastic stiffness matrix corresponding to the base state;Kgis the differential initial stress and load stiffness matrix due to the incremental loading pattern;λiare the eigenvalues;φiis theith buckling mode shape(eigenvectors);irefers to theith buckling mode.

The above Eq.(7)indicates that structural stability problem is a generalized eigenvalue problem in mathematics.With the values of λ increasing gradually,the above coef ficient matrix becomes singular;the equation has nonzero solution which means that the de flection form is also the equilibrium position.This equilibrium position is a kind of buckling mode.

These buckling modes are often the most useful outcome of the eigenvalue analysis,since they predict the likely instability modes of the structure.Thus,the imperfection has the form as

whereAiis the associated scaling factor andNthe order of the eigenvectors.

Rust and Schweizerhof35performed an eigenvalue analysis of a telescope model under ANSYS platform,and then,a buckling mode is taken as the shape of a geometric imperfection to seed the perfect mesh.They pointed out that if realistic imperfections are known they should be used directly,otherwise a conservative imperfection must be estimated from an eigenvalue buckling analysis.

Wong and Pellegrino36,37also used the eigenvalue buckling analysis(*BUCKLE)on ABAQUS platform to obtain the possible wrinkling modes of the membrane subjected to a simple shear and a diagonal pairs of opposite loads.After computing the buckling mode-shapes,a linear combination of all,or some selected eigenmodes is introduced into the structure as a geometrical imperfection.They suggest it is generally best to introduce in the membrane a rather general kind of imperfection,e.g.one obtained as the combination of many eigenvectors.

However,the eigenvalue buckling can only be applied to elastic problem.During an eigenvalue buckling analysis,the model’s response is de fined by its linear elastic stiffness in the base state and all nonlinear and/or inelastic material properties,as well as effects involving time or strain rate,are ignored in the procedure.Therefore,it may not be suitable for the thin-walled forming process which includes a mass of plastic deformation.But it is a useful tool to establish initial imperfection.

3.2.Static-implicit finite element method

The implicit procedure uses an automatic increment strategy based on the success rate of a full Newton iterative solution method38:

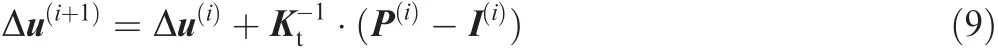
where Ktis the current tangent stiffness matrix,P the applied load vector,I the internal force vector,and Δu the increment of displacement.The implicit finite element analysis method iterates to find the approximate static equilibrium at the end of each load increment.It controls the increment by a convergence criterion throughout the simulation.

To enable the computational simulation to predict the wrinkle patterns,two numerical procedures are classically used in FEM:the bifurcation analysis of a perfect structure and the non-bifurcation analysis with initial imperfection.

3.2.1.A bifurcation analysis for a structure without imperfections

For the perfect structure without initial imperfections such as simple buckling problems,a bifurcation algorithm is necessary at a bifurcation point to lead the solution from the primary path to the secondary path.The bifurcation analysis was firstly introduced by Riks39,who termed it as a continuation method.He analyzed the post-bifurcation behavior of an elastic thinshell structure using an arc-length method.His method39is most commonly used in the bifurcation analyzes of elastic structures.

For a conservative system,the change of the total potential energy ΔΠ due to an admissible displacement variation δu of the displacement field u can be written as

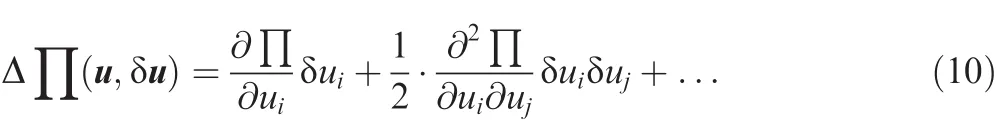
The second variation term must be positive de finite for a stable system and a condition can be written as

where Kijis the tangent stiffness.Therefore,the stability limit is reached at the point where the tangent stiffness Kijceases to be positive de finite,i.e.,when

among the timet,andt+ Δt,there must be a moment τ(t＜ τ＜t+ Δt)making

the characteristic equation of a nonlinear stability analysis becomes

The determinant in Eq.(14)can change sign abruptly within one incremental step in implicit analyzes.The bifurcation point is,therefore,found by checking the determinant of the stiffness matrix at each iteration of the increment.By solving the Eq.(14),a series of eigenvalues λiand the corresponding buckling mode shapes φiare obtain.

Zhan et al.40developed a three-dimensional rigid-plastic FE simulation system for the NC bending process of thin-walled tube.Wang and Lee41investigated the post bifurcation behavior of wrinkles in square metal sheets under Yoshida Test.Kim and Yoon4introduced bifurcation theory in an analysis of wrinkling during the sheet metal forming process.They analyzed puckering in a spherical cup deep drawing process,4wrinkling initiation and growth in a modi fied Yoshida buckling test,42bifurcation instability of a sheet metal during spring-back43and wrinkling in a cylindrical-cup deep drawing process.44,45

3.2.2.A non-bifurcation analysis with initial imperfections

In Abaqus/Standard the method can be used to solve postbuckling problems,both with stable and unstable postbuckling behavior.However,the exact post-buckling problem can often not be analyzed directly due to the discontinuous response(bifurcation)at the point of buckling.To analyze a post-buckling problem,we must turn it into a problem with continuous response instead of bifurcation,which can be accomplished by introducing a geometric imperfection pattern in the ‘perfect” geometry so that there is some response in the buckling mode before the critical load is reached(see Fig.3).In Fig.3,Pis the load,uthe displacement,Bthe bifurcation point,andOthe original point.

To overcome the dif ficulty of the path switching,an appropriate perturbation can be ‘seeded” in an implicit algorithm.It makes a conversion of the equilibrium path from the primary path I to the bifurcation path II.

Fig.3 Equilibrium path based on load–displacement:instability problem of a bifurcation point.

In the non-bifurcation analysis, αφi(α is a constant)are used as micro perturbations that trigger the conversion of the path in the subsequent numerical computation.Thus,the obtained bifurcation point by the perturbation analysis may deviate some from that of bifurcation analysis(see Fig.3).However,as the solution proceeds,the non-bifurcation solution in the perturbation analysis approaches the bifurcation solution,as shown in Fig.3.Therefore,the non-bifurcation solutions obtained by the perturbation analyzes can be considered as reliable.On the other hand,introducing those geometric imperfections into a ‘perfect” geometry model,the discontinuous bifurcation problem usually changes to a nonlinearcontinuousresponseproblem.Therefore,a nonbifurcation analysis employing initial imperfections sometimes gives a more reasonable result than a bifurcation analysis,as all real structures have inherent imperfections,such as material non-uniformities or geometric unevenness.46–49The nonbifurcation analysis was introduced by Koiter et al.,50who termed it as a perturbation method.Bellini and Chulya51proposed an improved automatic incremental algorithm and analyzed the post-buckling of a hinged cylindrical shell with a central load and a slanted column.They employed geometric and load imperfections to change the bifurcation problem to a limit point problem.Casciaro et al.52analyzed the postbuckling behavior of a long slender elastic structure using initial load imperfections.Cao and Boyce25investigated wrinkling behavior of rectangular plates under lateral constraint.A simple and practical form of imperfection for predictive modeling of buckling is given along with a discussion of the sensitivity of the solution to the magnitude and distribution of imperfections.

Many studies by Kyriakides and his co-workers have also demonstrated conclusively that the in fluence of geometric imperfections should be introduced to the perfect model to produce accurate buckling predictions.The success of such schemes in pipeline and generally relatively thick-walled circular shell applications has been demonstrated for axial compression,46–48compression under internal pressure,49internal pressure,53,54,47bending,55,56bending under internal pressure57,58and lined pipe under bending.59,60

The prediction of wrinkling in thin-walled part forming under CBC,however,involves dif ficulties.As mentioned in Sections 3.2.1 and 3.2.2,Riks Kyriakides and Yoon are all based on the implicit algorithm.However,thin-walled parts forming process with CBC always possesses their own various complicated contact and friction boundary conditions,and implicit algorithm cannot be used to solve large complex contact problem(deteriorated convergence in each iteration).Therefore,they concluded that the implicit algorithm is usually avoided in CBC finite element codes.In order to analyze wrinkling initiation under the complex boundary condition,additional efforts to reveal the wrinkling mechanism are required.

3.3.Dynamic-explicit finite element method

The explicit procedure is based on the implementation of an explicit integration rule along with the use of diagonal element mass matrices.The equation of motion for the body is integrated using an explicit central difference integration rule61:

where˙u is the velocity,¨u the acceleration,andrefer to the increment number and mid-increment numbers.

where M is the mass matrix,P the applied load vector and I the internal force vector.The explicit integration operator is conditionally stable,so that the time increments must satisfy where ωmaxis the element maximum eigenvalue.A conservative estimate of the stable time increment is given by the minimum value for all the elements.

The explicit FE analysis method determines a solution by advancing the kinematic state from one time increment to the next,without iteration.The explicit solution method uses a diagonal mass matrix to solve for the accelerations and there are no convergence checks.Therefore it is more robust and ef ficient for complicated problems,such as dynamic events,non-linear behavior,and complex contact conditions.

3.3.1.An elastic–plastic explicit FE model with perfect structure

As a dynamic approach,the explicit method generates deformed wrinkles due to the accumulation of numerical error.Because it did not involve decomposing tangent stiffness matrix,it cannot detect the singularities point and switch to secondary bifurcation path of buckling.In a numerical explicit analysis of instability problems with CBC,wrinkling often does not initiate immediately when the bifurcation(branching)point in the equilibrium path is reached.

Wang and Cao24,62also pointed that the explicit method as a dynamic approach can automatically generate deformed shapes with wrinkles due to the accumulation of numerical error.They concluded that the onset and growth of the wrinkling obtained from the explicit code is unreliable and lowerestimated simulation of wrinkling may appear in the sheet metal forming.In practice,in the explicit simulation of inplane roll-bending with perfect geometry,it never buckles numerically at reasonable con figuration as observed in the experimental results(multiple instability modes).63,64And in the explicit simulation of RDB with perfect geometry,especially in the simulation of thin-walled tube with large diameter,wrinkling did not occur.Or when wrinkling occurs,the wrinkling patterns often have a wavelength that spans only a few elements(a much shorter wavelength than would occur in reality).11,65The same thing also happens in the other forming process.Based on the explicit algorithm,Tian et al.66investigated the inner flange and side wrinkling in rotary-draw bending of rectangular aluminum alloy wave-guide tubes.De Magalha˜es Correia et al.67investigated the onset of wrinkling in sheet metal forming.Gonc¸alves et al.68studied the new developments in asymmetric plastic instability in tube joining.Wang et al.69and investigated the wrinkling failure in conventional spinning of a cylindrical cup.Long et al.70found that explicit FE model with perfect structure is sensitive to the input parameters such as mesh density,simulation speed,element type and time and mass scaling factor,and so on.Therefore,a convergence analysis about input parameters to ensure a good tradeoff between numerical accuracy and simulation is ef ficiency.

3.3.2.A hybrid method-combined with initial imperfection and energy conservation

In the present study,a hybrid numerical procedure,a combination of explicit FE method,initial imperfection and energy conservation,is proposed by Yang He’s research group.The plastic wrinkling in thin-walled part forming under CBC is predicted by introducing a microimperfection into the workpiece to perturb the explicit FE model.1,3This hybrid method not only takes advantage of the accurate buckling instability analysis but also overcomes the unreliability and inaccuracy of pure explicit methods.

The effectiveness of the proposed procedure is demonstrated by computing the wrinkling instability of five speci fications of in-plane roll-bending parts,which we had investigated in detail,both experimentally(see Fig.4).

It is shown that as a design tool,the accuracy of the wrinkles computed in this way is such that the numerical simulation can now be a replacement for practical experimentation,although,the computer run times are still impractically long and the present procedure is still fussy,duplication and repetition.A signi ficant,immediate bene fit of the present work is that all the multiple wrinkling modes in IRS forming processes can now be predicted.

Taking a large diameter thin-walled Al-alloy tube(diameter Φ=150 mm,thicknesst=1.5 mm andbendingradius 1.75D)as objective,the effectiveness of the proposed hybrid method is validated by comparing it with the tube bending experimental results.Through the analysis of distribution of compressive stress in the intrados of the tube in RDB process,two special simpli fied models,i.e.,tube under pure bending and tube under axial compression,are employed to estimate the buckling mode of a tube in RDB process.By using the eigenvalue buckling analysis and the Timoshenko‘s energy method,two kinds of imperfection are generated based on the above simpli fied compressive instability models,respectively.After that,these micro imperfections are scaled in the range of 1.25–5%of the thickness of the shell and embedded to the tube to perturb the nodal coordinates of the 3D elastic–plastic explicit FE model.The proposed hybrid method is veri fied by two sets of bending experiments(wrinkle and wrinkle-free).The results demonstrate excellent agreements between the simulation and experiments(see Fig.5).The hybrid method provides a robust and reliable predictor for the onset of wrinkling in tube RDB process with multi-die constraints.

The flowchart of a common hybrid method for wrinkling prediction is presented in Fig.6.

4.Summary of current prediction methods

The prediction of plastic wrinkling in sheet metal forming process with multi-die constraints is dif ficult.An assessment of the current research methods in terms of their advantages and limitations is shown in Table 1.

5.Trends and challenging in plastic wrinkling prediction under CBC

5.1.Trends

Lightweight thin-walled parts have attracted more and more applications in various industrial sectors such as aviation,aerospace and automobile.This kind of thin-walled structure usually has a very small diameter thickness ratio(thin wall pipe Φ/t＞ 20)or width thickness ratio(thin plate 80 ＞W/t＞8),thus,the bending stiffness of such structure is small.Small bending stiffness will increase the likelihood of wrinkling during forming process.Furthermore,thin-walled parts forming process always possesses various contact and friction boundary conditions,thus unequal compression stress inevitably occurs in the thin-walled structure.Small bending stiffness and large local distributed compressive stress will increase the likelihood of wrinkling during thin-walled part forming production.Wrinkling may be a serious obstacle to implementing the forming process and assembling the parts and may also play a signi ficant role in the wear of the tool.The wrinkle prediction is a hot topic in sheet metal forming.Consequently,the trend towards designing very light-weight thin-walled structures requires that thin-walled structure manufacture avoids wrinkling.Table 2 shows the summary and deviation of the simple boundary condition and complicated boundary condition in the forming processes.

Fig.4 Comparison of simulation results and experiment results.1

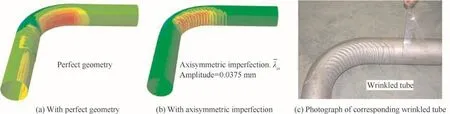
Fig.5 Simulation results and experimental results.3,71

Fig.6 Solution procedure of a common hybrid method for wrinkling instability prediction under CBC.1

Table 1 Assessment of prediction methods in terms of their advantages and limitations.

Previous numerical studies of wrinkling prediction have largely focused on a structure with SBC,i.e.,simple or fixed support conditions with free contact.For example,pure bending and axial compression of a tube are all the forming processes with SBC.Figs.7 and 8 show the wrinkling instability occur-ring under SBC.In these cases,the instability only deformed along one bifurcation path and can be effectively predicted by analytical approach or conventional FE method.

Table 2 Summary of simple boundary condition and complicated boundary condition.

Fig.7 Wrinkling instability in pure bending of a tube.55

Fig.8 Wrinkling instability in axial compression of a tube.46,48

However,in the case of wrinkling instability occurring under CBC,taking the IRS(see Fig.9)as an example,it is a highly unstable problem in which more than one bifurcation path exists in close proximity as shown in Fig.10.Therefore,it results in several instability modes including external wrinkling, internal wrinkling, turning-I and turning-II(see Fig.11).

In RDB process(see Fig.12),the surfaces of thin-walled tube are contacted with multiple relatively rigid dies,while the boundary conditions are changing in time and space.Therefore,the wrinkling instability during tube bending is strongly affected by process conditions and can be dramatically induced by a small deviation of the process conditions such as the contact condition,the original position of the blank and the perturbation of clearances between tube and dies.As a result,the multiform and asymmetric local distribution features of the wrinkling are observed in the experimental results.Fig.13 shows that the wrinkling could occur at straight or curved portion of tube and sometimes it may happen in the front or the whole portion of tube.If the wiper die and pressure die are not installed at the same horizontal level,the ripples may happen at upper or lower curved portion of tube.11The same thing also happens in the spinning forming (see Figs.14 and 15).72,73

Fig.9 Schematic diagram of the in-plane roll-bending of strip.63,64

Fig.10 Multiple instability problems under CBC.

Fig.11 Photographs of four kinds of wrinkling instability modes in the IRS process.

Fig.12 Schematic diagram of the rotary draw bending of tube.72,73

5.2.Challenging

Regarding the above trends in thin-walled parts forming process,thechallengesofplasticwrinkling prediction are summarized.

5.2.1.Modeling of imperfection

Using the proposed hybrid method and an appropriate imperfection,we are now able to accurately simulate the wrinkling behavior under complicated boundary conditions in a predictive manner.However,the modeling of the imperfection is dif ficult.

In general,it is common to consider the appropriate imperfection as that imperfection shape which is af fine to the lowest bifurcation mode.However,the bifurcation mode under CBC is not easy to calculate.Yuan and Kyriakides60recently also pointed out that if there are complicated contact nonlinearities,it makes the bifurcation check more dif ficult and challeng-ing.By considering the distribution of compressive stress in the thin-walled part forming,some simpli fied models with SBC are employed to obtain the buckling modes of the workpiece in actual forming process.Then,a series of imperfections is de fined in the shapes of these buckling modes.According to the minimum energy principle,the shape of the imperfections that would lead to the lowest deformation energy is searched.Note that the deformation energy needed for wrinkling is the lowest among all the possible deformation phenomena in the given forming conditions.Using the imperfection corresponding to the lowest level of energy may be considered as a solution to this issue.However,the computer run times of the strategy are still impractically long and the present procedure is still fussy,duplication and repetition.

Fig.13 Photographs of wrinkling instability in the RDB process.

Fig.14 Schematic diagram of the thin-walled part spinning.74,75

5.2.2.Establishment of an integrated hybrid FE model

To accurately predict wrinkling in thin-walled part forming under CBC,the nonlinear material behavior,buckling instability of the work piece during the forming process and complex contact between the tools and the deformable body should be cooperated in an integrated finite element model.However,the integrated hybrid finite element model is not easy to set up,which is the bottleneck for the plastic wrinkling prediction under CBC.

The FE model imports imperfection data through the user node labels.It does not check model compatibility between both analysis runs.Sometimes,the imperfection is de fined by eigenmode data or the superposition of weighted mode shapes.But usually we need to specify the imperfection directly as a table of node numbers and coordinate perturbations in the global coordinate system or,optionally,in a cylindrical or spherical coordinate system.Node set de finitions in the original FE model and the modeling of imperfection may be different.In such cases we have to ensure that the models for both analysis runs are identical and that the nodal information for the generated nodes is written to the final results file.In general,both the original model and the subsequent model(imperfection)are de fined consistently in terms of an assembly of part instances.

Fig.15 Photographs of wrinkling instability in the spinning process.

6.Conclusions

(1)The analytical approach can give a useful estimate of elastic–plastic buckling when the structure has an elementary shape such as cylinders,cones and spheres,and simple loading and boundary conditions such as uniform axial compression,uniform normal pressure,uniform torsion and pure bending,or a combination of some of them.However,large assumptions and simpli fications still have some discrepancy compared with the actual forming condition and complicated friction and clearance cannot be taken as a consideration in the analyticalapproach.Therefore,the analytical approach whether static equilibrium method or the energy method is not suitable for the wrinkling prediction under CBC.

(2)The eigenvalue buckling analysis can only be applied to elastic problem.Therefore,it may not be suitable for the thin-walled forming process which includes a mass of plastic deformation.But it is a useful tool to establish initial imperfection.The implicit FE methods are not quali fied for the wrinkling prediction under CBC,since the multiple tooling constraints,the complicated contact conditions and the perturbation of the tool,etc.always result in the convergence problems.Within a simple forward marching scheme,no iteration of nonlinear systems and no convergence control is required in the explicit FE method.Therefore it is more ef ficient for complicated forming process with CBC.However,it avoids decomposing the stiffness matrix of a system,so it cannot compute the bifurcation point and buckling modes of the structure.

(3)By using a combination of explicit FE method,initial

imperfection and energy conservation,a hybrid method is recommended to predict plastic wrinkling in thinwalled part forming under CBC.By considering an appropriate imperfection,the hybrid method is more sensitive to the compression instability compared with the one based on perfect geometry.In engineering practice,the application of hybrid method gives a useful insight into the plastic wrinkling prediction in complicated forming process,especially for the issues with CBC.

Acknowledgements

The authors would like to thank the National Natural Science Foundation of China(Nos.50905144,51275415);National Basic Research Program of China(No.2010CB731701);Program for New Century Excellent Talents in University,FundamentalResearch Funds for the CentralUniversities(3102014KYJD001)of China;the EU Marie Curie Actions–MatProFutureProject(FP7-PEOPLE-2012-IRSES-318968)of China and the ‘111” Project(B08040)of China for the support to this research.

1.Liu N,Yang H,Li H,Li ZJ.A hybrid method for accurate prediction of multiple instability modes in in-plane roll-bending of strip.J Mater Process Technol2014;214(6):1173–89.

2.Li H,Yang H,Zhang ZY,Li GJ,Liu N,Welo T.Multiple instability-constrained tube bending limits.J Mater Process Technol2014;214(2):445–55.

3.Liu N,Yang H,Li H,Tao ZJ,Hu X.An imperfection-based perturbation method for plastic wrinkling prediction in tube bending under multi-die constraints.IntJMechSci2015;98:178–94.

4.Kim J,Yang D,Yoon J,Barlat F.The effect of plastic anisotropy on compressive instability in sheet metal forming.Int J Plasticity2000;16(6):649–76.

5.Stoughton TB,Yoon JW.Review of Drucker’s postulate and the issue of plastic stability in metal forming.Int J Plasticity2006;22(3):391–433.

6.Yang H,Xian FJ,Liu YL.A coordination model of the in-plane bending of strip metal under unequal compression.J Mater Process Technol2001;114(2):103–8.

7.Xian FJ,Yang H,Xiao HS.Finite element analysis of effects of parameters on in-plane bending process of strip metal.J Mater Process Technol2000;102(1–3):78–83.

8.Yang H,Xian FJ,Xiao HS.Instable modes of in-plane bending of strip metal under unequal compressing.J Mater Process Technol2000;99(1–3):197–201.

9.Li H,Yang H,Zhan M,Gu RJ.A new method to accurately obtain wrinkling limit diagram in NC bending process of thinwalled tube with large diameter under different loading paths.J Mater Process Technol2006;177(1–3):192–6.

10.Yang H,Li H,Zhang ZY,Zhan M,Liu J,Li GJ.Advances and trends on tube bending forming technologies.Chin J Aeronaut2012;25(1):1–12.

11.Li H,Yang H.A Study on multi-defect constrained bendability of thin-walled tube NC bending under different clearance.Chin J Aeronaut2011;24(1):102–12.

12.Liang BW,Hu SG.Elastoplastic stability theory.Beijing:National Defense Industry Press;1983.p.339–66[Chinese].

13.Wang X,Xiao J,Zhang YC.A method for solving the buckling problem of a thin-walled shell.Int J Pres Ves Pip2004;81(12):907–12.

14.Peek R.Wrinkling of tubes in bending from finite strain threedimensional continuum theory.Int J Solids Struct2002;39(3):709–23.

15.Timoshenko S,Gere JM.Theory of elastic stability.New York:McGraw-Hill;1961.p.36–45.

16.Senior BW.Flange wrinkling in deep-drawing operations.J Mech Phys Solids1956;4(3):235–46.

17.Morovvati MR,Mollaei-Dariani B,Asadian-Ardakani MH.A theoretical,numerical,and experimental investigation of plastic wrinkling of circular two-layer sheet metal in the deep drawing.J Mater Process Technol2010;210(13):1738–47.

18.Shafaat MA,Abbasi M,Ketabchi M.Investigation into wall wrinkling in deep drawing process of conical cups.J Mater Process Technol2011;211(11):1783–95.

19.Yu TX,Johnson W.The buckling of annular plates in relation to the deep-drawing process.Int J Mech Sci1982;24(3):175–88.

20.Kowsarinia E,Alizadeh Y,Pour HSS.Theoretical and experimental study on the effects of explosive forming parameters on plastic wrinkling of annular plates.Int J Adv Manuf Technol2013;67(1–4):877–85.

21.Cao J,Wang X.An analytical model for plate wrinkling under triaxial loading and its application.Int J Mech Sci2000;42(3):617–33.

22.Cao J.Prediction of plastic wrinkling using the energy method.J Appl Mech1999;66(3):646–52.

23.Wong W,Pellegrino S.Wrinkled membranes II:analytical models.J Mech Mater Struct2006;1(1):27–61.

24.Wang X,Cao J.On the prediction of side-wall wrinkling in sheet metal forming processes.Int J Mech Sci2000;42(12):2369–94.

25.Cao J,Boyce MC.Wrinkling behavior of rectangular plates under lateral constraint.Int J Solids Struct1997;34(2):153–76.

26.Cao J,Cheng SH,Wang HP,Wang CT.Buckling of sheet metals in contact with tool surfaces.CIRP Ann Manuf Technol2007;56(1):253–6.

27.Li H,Yang H,Zhan M.A study on plastic wrinkling in thinwalled tube bending via an energy-based wrinkling prediction model.Model Simul Mater Sci Eng2009;17(3):1–33.

28.Li H,Yang H,Zhang ZY,Wang ZK.‘Size effect’related bending formability of thin-walled aluminum alloy tube.Chin J Aeronaut2013;26(1):230–41.

29.Zhao GY,Liu YL,Dong CS,Yang H,Fan XG.Analysis of wrinkling limit of rotary-draw bending process for thinwalled rectangular tube.J Mater Process Technol2010;210(9):1224–31.

30.Donnell L,Wan C.Effect of imperfections on buckling of thin cylinders and columns under axial compression.J Appl Mech ASME1950;1(17):73–83.

31.Peek R,Hilberink A.Axisymmetric wrinkling of snug- fit lined pipe.Int J Solids Struct2013;50(7–8):1067–77.

32.Kyriakides S,Corona E.Mechanics of offshore pipelines.Amsterdam:Elsevier;2007.p.280–316.

33.Hutchinson JW,He MY.Buckling of cylindrical sandwich shells with metal foam cores.Int J Solids Struct2000;37(46):6777–94.

34.Dassault Aircraft Company.Abaqus analysis user’s manual(version 6.9).2010.p.692–712.

35.Rust W,Schweizerhof K.Finite element limit load analysis of thin-walled structures by ANSYS(implicit),LS-DYNA(explicit)and in combination.Thin Wall Struct2003;41(2–3):227–44.

36.Wong W,Pellegrino S.Wrinkled membranes III:numerical simulations.J Mech Mater Struct2006;1(1):63–95.

37.Wong W,Pellegrino S.Wrinkled membranes I:experiments.J Mech Mater Struct2006;1(1):3–25.

38.Dassault Aircraft Company.Abaqus benchmark manual(version 6.9).2010.p.1261–82.

39.Riks E.An incremental approach to the solution of snapping and buckling problems.Int J Solids Struct1979;15(7):529–51.

40.Zhan M,Yang H,Jiang ZQ,Zhao ZS,Lin Y.A study on a 3D FE simulation method of the NC bending process of thin-walled tube.J Mater Process Technol2002;129(1–3):273–6.

41.Wang X,Lee LHN.Postbifurcation behavior of wrinkles in square metal sheets under Yoshida Test.Int J Plasticity1993;9(1):1–19.

42.Kim JB,Yoon JW,Yang DY.Wrinkling initiation and growth in modi fied Yoshida buckling test: finite elementanalysis and experimentalcomparison.IntJMechSci2000;42(9):1683–714.

43.Kim JB,Yang DY,Yoon JW.Bifurcation Instability of sheet metal during spring-back.Philos Mag2013;93(15):1914–35.

44.Kim JB,Yoon JW,Yang DY.Investigation into the wrinkling behaviour of thin sheets in the cylindrical cup deep drawing process using bifurcation theory.Int J Numer Meth Eng2003;56(12):1673–705.

45.Kim JB,Yoon JW,Yang DY,Barlat F.Investigation into wrinkling behavior in the elliptical cup deep drawing process by finite element analysis using bifurcation theory.J Mater Process Technol2001;111(1–3):170–4.

46.Bardi FC,Kyriakides S.Plastic buckling of circular tubes under axial compression—part I:experiments.Int J Mech Sci2006;48(8):830–41.

47.Jiao R,Kyriakides S.Ratcheting,wrinkling and collapse of tubes under axial cycling.Int J Solids Struct2009;46(14–15):2856–70.

48.Bardi FC,Kyriakides S,Yun HD.Plastic buckling of circular tubes under axial compression—part II:analysis.Int J Mech Sci2006;48(8):842–54.

49.Paquette JA,Kyriakides S.Plastic buckling of tubes under axial compression and internal pressure.Int J Mech Sci2006;48(8):855–67.

50.Koiter WT,Elishakoff I,Li YW,Starnes JH.Buckling of an axially compressed cylindrical shell of variable thickness.Int J Solids Struct1994;31(6):797–805.

51.Bellini PX,Chulya A.An improved automatic incremental algorithm for the ef ficient solution of nonlinear finite element equations.Comput Struct1987;26(1–2):99–110.

52.Casciaro R,Garcea G,Attanasio G,Giordano F.Perturbation approach to elastic post-buckling analysis.Comput Struct1998;66(5):585–95.

53.Jiao R,Kyriakides S.Ratcheting and wrinkling of tubes due to axial cycling under internal pressure:part I experiments.Int J Solids Struct2011;48(20):2814–26.

54.Jiao R,Kyriakides S.Ratcheting and wrinkling of tubes due to axial cycling under internal pressure:part II analysis.Int J Solids Struct2011;48(20):2827–36.

55.Corona E,Lee LH,Kyriakides S.Yield anisotropy effects on buckling of circular tubes under bending.Int J Solids Struct2006;43(22–23):7099–118.

56.Ralf P.Wrinkling of tubes in bending from finite strain threedimensional continuum theory.Int J Solids Struct2002;39(3):709–23.

57.Limam A,Lee LH,Corona E,Kyriakides S.Inelastic wrinkling and collapse of tubes under combined bending and internal pressure.Int J Mech Sci2010;52(5):637–47.

58.Corona E,Kyriakides S.On the collapse of inelastic tubes under combined bending and pressure.Int J Solids Struct1988;24(5):505–35.

59.Yuan L,Kyriakides S.Liner wrinkling and collapse of bi-material pipe under bending.Int J Solids Struct2014;51(3–4):599–611.

60.Yuan L,Kyriakides S.Plastic bifurcation buckling of lined pipe under bending.Eur J Mech A Solids2014;47:288–97.

61.Kang S,Im S.Finite element analysis of dynamic response of wrinkling membranes.Comput Method Appl Mech Eng1999;173(1–2):227–40.

62.Lu H,Cheng HS,Cao J,Liu WK.Adaptive enrichment meshfree simulation and experiment on buckling and post-buckling analysis in sheet metal forming.Comput Method Appl Mech Eng2005;194(21–24):2569–90.

63.Li ZJ,Yang H,Li HW,Li H.A new model for precision control of the radius in in-plane roll-bending of strip considering rolls and stand de flections.JMaterProcessTechnol2011;211(12):2072–84.

64.Li ZJ,Yang H,Li H,Xu J.An accurate 3D-FE based radius prediction model for in-plane roll-bending of strip considering spread effects.Comp Mater Sci2010;50(2):666–77.

65.Li H,Yang H,Zhan M,Gu RJ.The interactive effects of wrinkling and other defects in thin-walled tube NC bending process.J Mater Process Technol2007;187–188:502–7.

66.Tian S,Liu YL,Yang H.Effects of geometrical parameters on wrinkling of thin-walled rectangular aluminum alloy waveguide tubes in rotary-draw bending.Chin J Aeronaut2013;26(1):242–8.

67.De Magalha˜es Correia JP,Ferron G.Wrinkling of anisotropic metal sheets under deep-drawing:analytical and numerical study.J Mater Process Technol2004;155–156:1604–10.

68.Gonc¸alves A,Alves LM,Martins PAF.Tube joining by asymmetric plastic instability.J Mater Process Technol2014;214(1):132–40.

69.Wang L,Long H,Ashley D,Roberts M,White P.Effects of the roller feed ratio on wrinkling failure in conventional spinning of a cylindricalcup.ProcInstMechEngPartB2011;225(11):1991–2006.

70.Watson M,Long H.Wrinkling failure mechanics in metal spinning.Procedia Eng2014;81:2391–6.

71.Liu N,Yang H,Li H,Zhan M,Tao ZJ,Hu X.Modelling of wrinkling in NC bending of thin-walled tubes with large diameters under multi-die constraints using hybrid method.Procedia Eng2014;81:2171–6.

72.Li H,Yang H,Zhan M,Kou YL.Deformation behaviors of thinwalled tube in rotary draw bending under push assistant loading conditions.J Mater Process Technol2010;210(1):143–58.

73.Li H,Yang H,Zhan M,Sun ZC,Gu RJ.Role of mandrel in NC precision bending process of thin-walled tube.Int J Mach Tools Manuf2007;47(7–8):1164–75.

74.Kleiner M,Go¨bel R,Kantz H,Klimmek C,Homberg W.Combined methods for the prediction of dynamic instabilities in sheetmetalspinning.CIRPAnnManufTechnol2002;51(1):209–14.

75.Wang L,Long H.A study of effects of roller path pro files on tool forces and part wall thickness variation in conventional metal spinning.J Mater Process Technol2011;211(12):2140–51.