A hybrid original approach for prediction of the aerodynamic coefficients of an ATR-42 scaled wing model

Adllh Ben Mosh,Ruxndr Mihel Botez,*,Thien My Do

aDepartment of Automated Production Engineering,E´cole de Technologie Supe´rieure,University of Quebec,Laboratory of Applied Research in Active Controls,Avionics and AeroServoElasticity LARCASE,Montreal,Quebec H3C-1K3,CanadabDepartment of Mechanical Engineering,E´cole de Technologie Supe´rieure,University of Quebec,Montreal,Quebec H3C-1K3,Canada

1.Introduction

For a long time,researchers in arti ficial intelligence have worked into machines programming in order to perform different tasks.Different areas have been treated,such as decisionsupport,pattern recognition,control,robotics,and prediction.However,the programming of machines that can adapt to all situations and constraints is dif ficult.For this reason,research has been done in machine learning.Supervised learning is a technique in which rules are automatically generated from a database.This learning database is characterized by a pair of inputs-outputs(xn,yn),whereyn=f(xn).The objective of a supervised learning method is to determine a representation of the functionf,called ‘prediction functionh”.This new functionhprovides an outputy′=h(x′)for a new inputx′.There are two types of problems that may be solved by means of ‘supervised learning”.The first type is a ‘regression problem”,in which the output associated with an input is a real number.The second type is a ‘classi fication problem”,in which the output has a finite cardinal,and where a label should be assigned to a given input.1In this work,a prediction model is presented to solve a regression problem.To solve this type of problem,many supervised learning methods can be used,such as neural networks(NNs),fuzzy logic,and support vector machines(SVMs).These three methods can be applied to conceive prediction or identi fication models.NNs and fuzzy logic have been used extensively to solve control systems problems in the aerospace field.

Neural networks have been used in multiple domains,including pattern classi fication,optimal control,and manufacturing,2–6in the reliability field by Nourelfath and Nahas7,8and by Ren and Bai.9In aerospace engineering,NNs can be applied to a large range of complex problems,as presented by Faller and Schreck.10Other problems were resolved using the NN method,such as:the detection and identi fication of structural damage,11helicopter design,12composite structural optimization,13modeling of aerodynamic characteristics from flight data,14,15the detection of unanticipated effects such as icing,16,17and autopilot controllers and advanced control laws for carefree maneuvering,18,19as well as aerodynamic liftCLand dragCDcoef ficients prediction.20An experimental study on the use of smart sensing and neural networks to strain loads for different air flow cases were presented by Lunia et al.,21where the authors used a fiber-optic sensor to train and verify the neural network performance.They also used a multilayer network to map the inputs and outputs of a nonlinear system,thereby to create a three-layered neural network,with three neurons in the first layer, five in the second layer,and one neuron in the third layer.A hyperbolic tangent sigmoid function was used in the first and second layers,while a linear function was used in the third layer.The network was developed through ‘supervised learning”,in which parameters were adjusted to achieve the target outputs for given inputs.Scott22developed an adaptive neural network-based control system that integrated three developed and tested control systems.One system used flutter suppression control laws,a second system employed a predictive NN control scheme,and a third system used an NN in an inverse model control scheme.Suresh et al.23used recurrent neural networks for the prediction of lift coef ficients at high angles of attack.In their approach,the lift coef ficients were obtained from wind tunnel tests.

Fei et al.24evaluated the air speed,the angle of attack,and the angle of sideslip in the control of flying bodies.They have proposed a new experimental methodology by which the flight parameters were inferred from multiple hot- film flow speed sensors mounted on the surface of the wing of a micro air vehicle(MAV).In order to obtain a good mathematical relationship between the sensor readings and the flight parameters,they proposed the use of micro hot- film flow speed sensor arrays and a back-propagation neural network to determine the following three flight parameters:air speed,angle of attack,and angle of sideslip.24Peyada and Ghosh25proposed the feed forward neural networks method to estimate aircraft parameters from flight data.This method used feed forward neural networks to establish a neural model that was used to predict the time histories of motion variables at the(k+1)th time instant,where the measured initial conditions corresponded to thekth time instant.25A neural network based on a flush air data sensing system and demonstrated on a mini air vehicle was presented by Samy et al.26

Xuan et al.27presented a fuzzy neural network controller,which had the advantages of both fuzzy control and neural network methods.In this method,the uncertain parameters were controlled for nonlinear time-varying systems.Fuzzy logic can be used to model highly non-linear,multidimensional systems,including those with variations of parameters,or where the sensors’signals were not accurate enough for other models.28De Jesus and Botez29proposed a new technique for helicopter model identi fication from flight test data based on neural networks.The dynamics behavior of a helicopter was identi fied with a recurrence method,and an optimization procedure was based on the neural network theory and tuning of the initial conditions.29An aeroservoelastic model was presented by Boe¨ly et al.,30,31in which neural network and fuzzy logic algorithms identi fied the multi-input and multi-output systems of an F/A-18 aircraft.An approach has been proposed by Roudbari and Sagha fi32to identify the dynamics of fighter aircraft using NNs.

A flight parameter control system based on neural networks has been proposed by Ben Mosbah et al.,33in which the proposed NNs were optimized using a meta-heuristic algorithm,called the extended great deluge(EDG).Their approach predicted pressure distributions and aerodynamic coef ficients from the known parameters(angle of attack,Mach number,etc.).Kouba et al.34,35proposed an identi fication model,based on fuzzy logic methods,to identify the nonlinear aircraft models for a high number of flight tests;their modelwasused for an F/A-18aircraft.A new method for the realization of two neuro-fuzzy controllers for a morphing wing design application was also presented by Grigorie et al.36The proposed controllers’main function had the aim to correlate each set of pressure differences that were calculated between the optimized and reference wing airfoils,where each of the airfoil deformations was produced by the actuators’system.37Several other authors also used fuzzy logic in identi fication and control

areas.36,38–41

2.Support vector machines(SVMs)

Although the SVM method is speci fic to classi fication problems,it can be used in regression problems.The objective is to determine a representationh(x)in R,called ‘estimation function”of the original functionf(x)given in the learning phase.

The functionh(x)is estimated based on a training set ofNsamples.A tube of width ε is de fined around the desired outputs,so that all the predicted values should be inside this tube.

For a linear regression,the functionh(x)is estimated as follows42:

where w is the weight of the inputs space andbis a threshold∈R.

As described by Vapnik,43considering a set of data{x1,x2,...,xN}with targets values{y1,y2,...,yN},the optimization of the prediction functionh(x)in the larger space is characterized by the resolution of the following system1:

subject to:

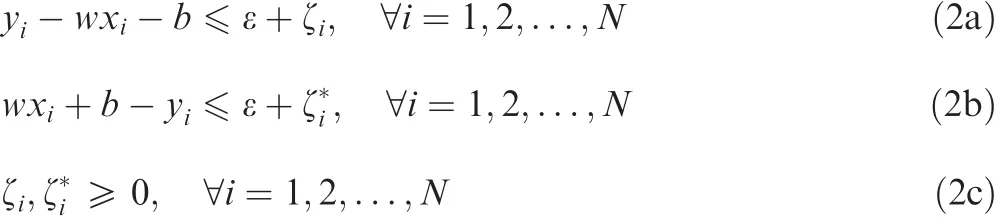
whereCis a regularization parameter,which can control the in fluence of the error,the termis used to control the complexity of the regression function,ε is the width of the tube de fined around the desired outputs,andof samples which are outside of the ε-tube.44

For a generalization of a non-linear regression,a kernel functionK(x,xi)is used.We use a Lagrangian function,where the Lagrangian is de fined as the sum of the objective function and a linear combination of constraints whose coef ficients(αi≥ 0)are called Lagrange multipliers.1

As explained by Smola et al.,45by introducing Lagrange multipliers,our optimization problem de fined in Eq.(2)becomes a dual form.The shape of the ‘regression function”is de fined as follows42:

where αiandare the Lagrange multipliers,which are calculated in the training process.bis calculated using the constraints of the optimization model(Eq.(2)).

The constraint given in Eq.(2a)becomes equality usingand the constraint given in Eq.(2b)becomes equality usingof samples corresponding for the nonzero Lagrange multipliers,andKis the kernel function representing a scalar product in the re-description space.

A kernel function is used to construct the decision surface‘hyper-plan” in the input space.Some examples of kernel functions are presented as follows1:

The linear kernel function is given by:

The polynomial kernel function is given by:

wheredis the degree of the kernel functionK.

The Gaussian kernel function is given by:

3.Optimization of the SVM parameters

For a good functioning of SVM and for obtaining good results,it is essential to use the appropriate SVM parameters to solve the investigated problem.To choose the SVM parameters such asC,ε,and the degreedof the kernel functionK,it is important to use an optimization algorithm.

To optimize these parameters,different techniques have been proposed.For example,a technique has been used by Keerthi46to the tuning of SVM parameters using radius/margin bound,which is taken as the index to be minimized.46Cherkasky and Ma47optimized the parametersCand ε when a Gaussian kernel function was selected using an analytical method.The meta-heuristic methods were also used to optimize the SVM parameters,such as the simulated annealing algorithm used by Ping and Hong48to find the best values ofCand ε parameters.

Since the quality of results necessarily depends on the quality of the SVM parameters,an original hybridization of the SVM method with a meta-heuristic algorithm is proposed.The proposed meta-heuristic algorithm is the EGD algorithm used to optimize the SVM parameters.The EGD algorithm is described in the following section.

4.Extended great deluge algorithm

The EGD is a local search procedure that was introduced by Dueck49in 1993,and is classi fied as a meta-heuristic algorithm.This local search algorithm can accept sometimes bad solutions whose values are smaller than a certain limitB.This flexibility allows the optimization of a process to get out of the local minimum.The limitBdecreases monotonically(in the case of minimization problems)during the search.The initial value ofBis equal to the ‘objective function”,and for each iteration,its value decreases by a fixed ΔBin ‘minimization”problems,and increases by the same value of ΔBfor ‘maximization”problems.The ΔBstep represents an ‘input parameter”in this approach.During the search,Bis the limit between a feasible and a non-feasible area of research,and serves to orientate the solution of the problem towards the‘feasible area”.In other words,the neighborhood of the solutionS*is cut by the limitBand the research is only conducted in one side,below or above the limitB,depending on the minimization or maximization of the objective function.The increase or decrease ofBwith ΔBcan be considered as a control process giving a desired solution.In the beginning phases of research,the solution has the ability to move in both directions,and can also be found inside the feasible portion limited byB.Otherwise,there is a great chance of accepting poor solutions,because the limitBis located at a long distance from the chosen solutionS*and a small part of its neighborhood may be cut off.During the search,the limitBmoves closer to the value of the current solution,so the search space becomes smaller and the possibility of improving the solution becomes lower,leading to the end of the process research.49

The first application completed with this approach was the optimization of an exam timetable problem that was treated by Burke et al.50The results proved the effectiveness of this algorithm.51Several of these results have been improved using approaches such as ‘taboos search”.

Fig.1 shows the steps of the EGD algorithm.51This algorithm was used to resolve a preventive maintenance optimization problem for multi-state systems by Nahas et al.52The proposed model consisted in finding an optimal sequence of maintenance actions which minimized maintenance costs.52Other applications of the EGD algorithm consisted in the optimization of the scheduling problems of manufacturing cells as proposed by Ben Mosbah53and by Ben Mosbah and Dao.51,54,55In these applications,the EGD algorithm gave better results than the genetic algorithm(GA)and the simulated annealing(SA).

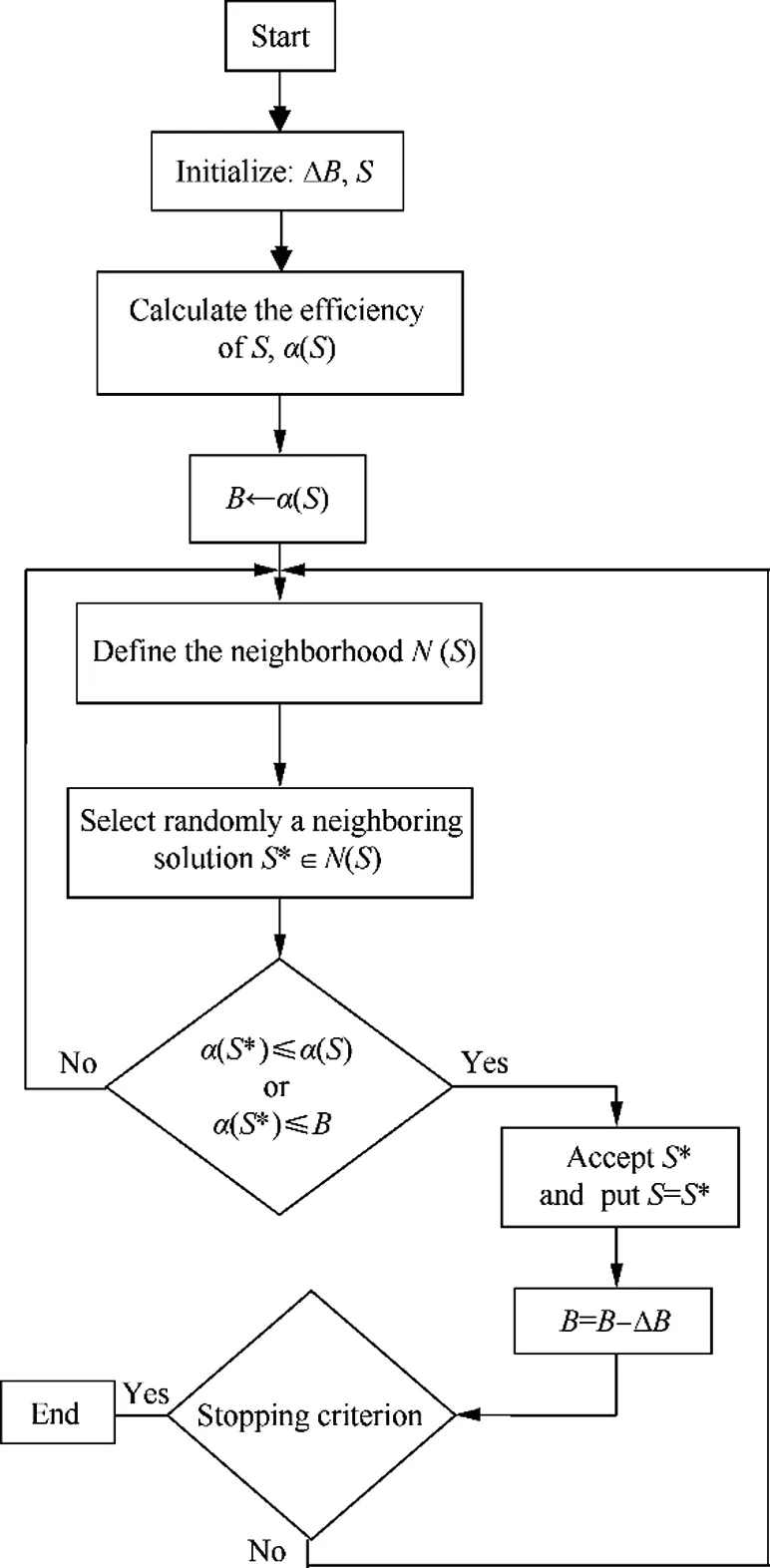
Fig.1 Extended great deluge algorithm.51

The advantage of the EGD is that only one parameter needs to be adjusted,ΔB,which is already de fined by Burke et al.50have shown that the convergence time of the algorithm is dependent on the ΔBvalue.Indeed,an increase of the ΔBvalue would result in a decrease of the convergence time,but the quality of solutions could also degrade,which explains the importance of choosing the best ΔBto obtain a good compromise between quality of results and calculation time.The EDG algorithm is a meta-heuristic type in which the optimum solution is not guaranteed,because the search process is based on a randomly selected initial solution,which is the initial boundaryBand the value of ΔB.56

As shown in Fig.1,the steps of the EGD algorithm are the following:

Step 1.Choose randomly the initial solutionSand ΔB.

Step 2.Calculate the ef ficiency ofS,which is α(S),and assign its value toB.

Step 3.De fine the neighborhoodN(S)ofS.

Step 4.Select randomly a neighboring solutionS*belonging toN(S).

Step 5.Compare the new solutionN(S*)with the previous solution,N(S)andB.

If two conditions(α(S*)≤ α(S)and α(S*)≤B)are not satis fied,select a new neighboring solutionS.

If one of these conditions is true,then accept the solutionS=S*and recalculateB=B–ΔB.

Step 6.If the stopping criterion is true,end of process.

Step 7.Else,a new neighboring solutionSis selected and the algorithm is tested again.55

The performance and the results obtained with our proposed algorithm are further evaluated to determine the lift,drag,and moment coef ficients for different angles of attack and Mach numbers and to compare their values with XFoil values.

5.New proposed SVM-EGD algorithm

In this paper,a hybrid SVM-EGD algorithm is proposed to calculate the lift,drag,and moment coef ficients for different flight cases(angles of attack and Mach number values).The steps of this hybrid approach are shown in Fig.2.In our new algorithm,we use a qualitative performance measure describing the learning abilities of a given trained SVM method,in which the training error is expressed as the mean sum of the squared residuals(the mean squared error(MSE))in the training data48:

Fig.2 Hybrid SVM-EGD algorithm.57

wherey(xk)is the desired value,y*(xk)is the estimated output of the SVM method for thekth inputxk,andnis the number of data points used in the training set.

As shown in Fig.2,the steps of the SVM-EGD approach are the following:

Step 1.Choose randomly the initial parametersSof SVM and ΔB,the initial error,and the iteration number.

Step 2.De fine learning vectors and assign the value of the initial error toB.

Step 3.De fine the neighborhoodNofS.

Step 4.Select randomly a neighboring solutionS*belonging toN(S).

Step 5.Learning of SVM using parametersS*and return the predicted vector y*.

Step 6.Calculate the error between the desired values and the predicted values.

Step 7.Compare the new solutionN(S*)with the old solution,N(S)andB.

If two conditions(MSE(S*)≤ MSE(S)and MSE(S*)≤B)are not satis fied,select a new neighboring solutionS.

If one of these conditions is true,then accept the solutionS=S*.

Step 8.If the iteration number is reached,end of the process,and keep the optimized parameters to be used for new input data.

Step 9.Else,recalculateB=B–ΔBand go to Step 3.

6.Infrastructure

In this section,the infrastructure used in the experimental tests is presented.This infrastructure includes a Price–Paı¨doussis wind tunnel,a Regional Transport Aircraft ATR-42 model,a fastening system,and a transducer.The infrastructure is used at the Research Laboratory in Active Controls,Avionics and Aeroservoelasticity(LARCASE).

6.1.Price–Paı¨doussis wind tunnel

The proposed approach is validated using experimental tests carried out in the Price–Paı¨doussis subsonic blow-down wind tunnel of LARCASE that is shown in Fig.3.This subsonic wind tunnel has two test chambers:one with a section equal to 0.3×0.6 m2that provides a speed up to 60 m/s,and the other with a section of 0.6×0.9 m2that provides a speed up to 40 m/s.56

Fig.3 Price–Paı¨doussis wind tunnel.

6.2.Transducer

During the experimental tests,a ‘six-axis force/torque sensor system”is used to determine the values of aerodynamic liftCL,dragCD,and momentCMcoef ficients.The transducer used in the experiments is a compact and robust structure that converts force and torque into analog strain gage signals.Through the strain gauges and high quality silicon used in the design,this sensor can withstand high overload.Fig.4 shows the transducer with a standard tool adapter.The fastening system of the ATR-42 model and the transducer are shown in Fig.5.

Fig.4 Transducer.

Fig.5 Fastening system of the model and transducer.

The assembly consisting of the sensor and the fastening system is mounted below the test chamber of the wind tunnel.

6.3.ATR-42 wing

The proposed approach is used to predict the aerodynamic coef ficients for the ATR-42 wing.The chord of the ATR-42 is 247 mm and the maximum thickness is equal to 14.5%of the chord.The composite ATR-42 wing model used in the wind tunnel tests is shown in Fig.6.

7.Implementation of the SVM-EGD algorithm and analysis of results

7.1.Theoretical results

The aerodynamic liftCL,dragCD,and momentCMcoef ficients are determined in this paper for different values of Mach numbers and angles of attack on the ATR-42 model.

For the ‘learning” of the SVM algorithm,a database obtained using XFoil software was used.A total of 101 values of liftCL,dragCD,and momentCMcoef ficients for combinations of angles of attack α between-5°and 5°(0.1°per step)and a Mach number=0.11(40 m/s)were used.These test cases were selected so that they could be validated using the Price–Paı¨doussis wind tunnel.The validation data set was composed of 11 random vectors and the test data set was composed of 11 random vectors.

The optimal values of the SVM parameters(degreedof the kernel,C,and ε)were obtained using the EGD algorithm.The Gaussian kernel(Eq.(6))gave better results than the other kernels(Eqs.(4)and(5))with the parameterd=2.The other parameters areC=8,036,518 and ε=9.29 × 10-6.

The proposed approach was implemented in MATLAB.The process of training and optimization of the SVM parameters takes approximately 9 h.Then,the results for these 11 cases are obtained rapidly.The aerodynamic liftCL,dragCD,and momentCMcoef ficients values are presented in Tables 1–3 and in Figs.7–9,for a number of 11 flight cases expressed in terms of angles of attack α’sand Mach numbers.

Fig.6 ATR-42 model installed in the test chamber of the wind tunnel.

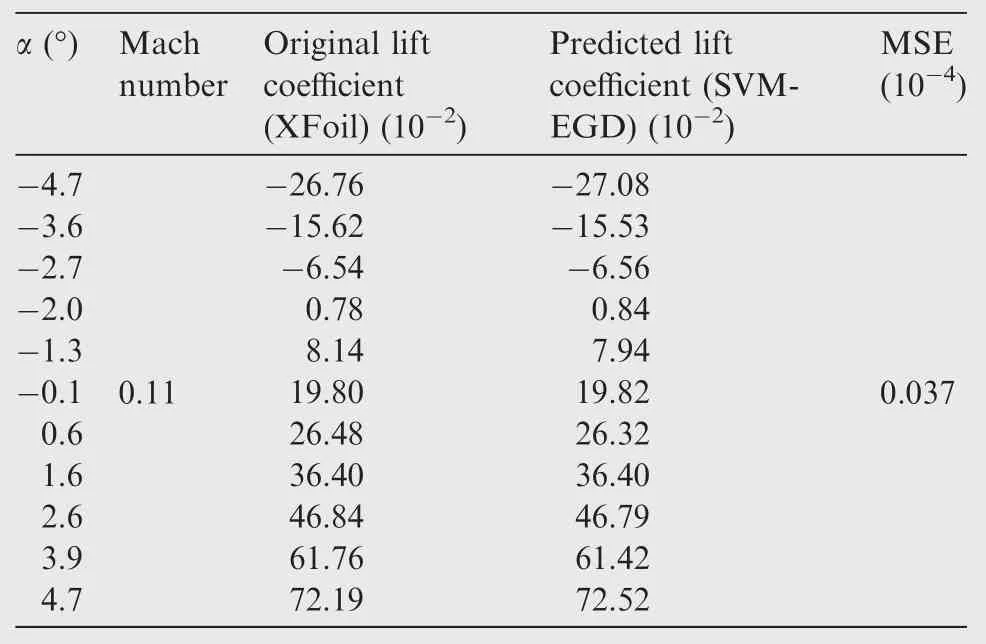
Table 1 Original versus predicted lift coef ficients for different air flow cases.

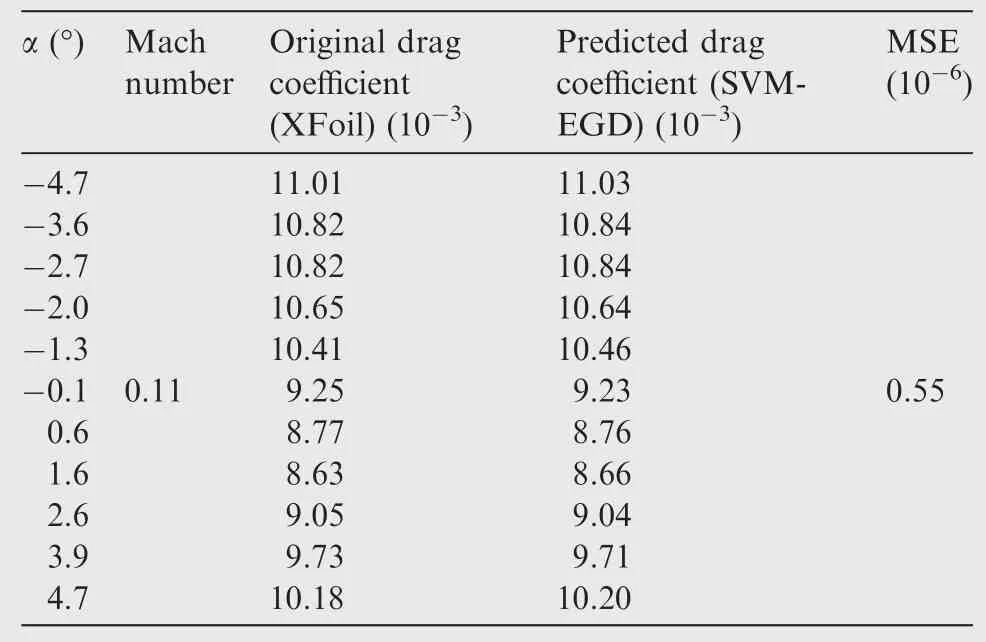
Table 2 Original versus predicted drag coef ficients for different air flow cases.

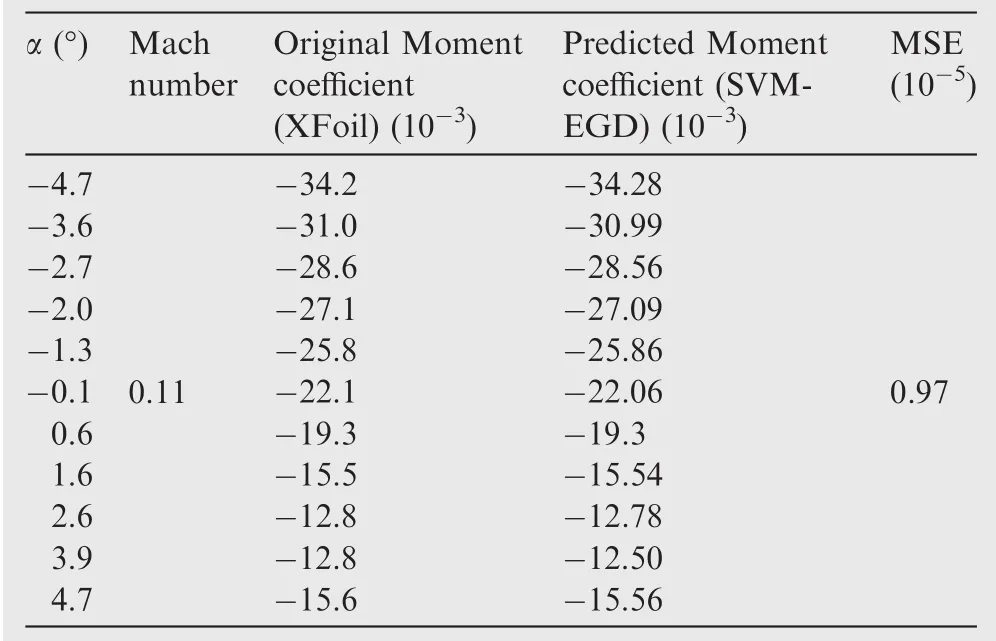
Table 3 Original versus predicted moment coef ficients for different air flow cases.

Fig.7 Lift coef ficient CLversus angle of attack α.

Fig.8 Drag coef ficient CDversus angle of attack α.

Fig.9 Moment coef ficient CMversus angle of attack α.

7.2.Experimental results

The experimental results using the Price–Paı¨doussis wind tunnel are presented.For the ‘learning” of the SVM,a database obtained using experimental tests was used.A total of 100 values of lift(CL),drag(CD),and moment(CM)aerodynamic coef ficients for combinations of angles of attack α between-9°and 15°(1°per step)and Mach numbers of 0.058,0.073,0.088,and 0.117 were used,for the Reynolds numbers of 316666,395833,475000,and 633333,respectively.

The learning of the SVM approach was done using 60 flight cases,and was tested using 40 flight cases randomly selected from the database.The computing time for the training and testing of the SVM algorithm was calculated using the optimal values of the SVM parameters(degreed=2 of the Gaussian kernel,C=8,036,518,and ε=9.29 × 10-6)and took less than 1 s to obtainCL,CD,andCMfor the 40 flight cases.The experimental and predicted SVM-EGD results are presented in Tables 4–6 and in Figs.10–12.Table 4 and Fig.10 show the lift coef ficientCLvariation with α angle of attack,Table 5 and Fig.11 present the drag coef ficientCDvariation with α angle of attack,while the moment coef ficientCMvariation with α angle of attack are presented in Table 6 and Fig.12.

The mean squared error(MSE)(Eq.(5))was calculated in order to show the precision of the obtained results.The obtained MSEs are presented in Table 7.

Table 4 Experimental versus predicted lift coef ficients for different air flow cases.

Table 5 Experimental versus predicted drag coef ficients for different air flow cases.

Table 6 Experimental versus predicted moment coef ficients for different air flow cases.

8.Conclusions

A new algorithm using the SVM-EGD approach was used to optimize the values of the SVM parameters by use of the EGD approach.The obtained results were validated using experimental wind tunnel tests.Since the mean squared errors between the predicted and the experimental results are very low where the fitted line is very close to desired data,we conclude that the SVM-EGD approach is robust and accurate.In addition,the mean squared errors for the results obtained with XFoil versus those from SVM-EGD are almost zero,where the MSE does not exceed a maximum of 0.03×10-2for the lift coef ficient,of 0.97×10-5for the drag coef ficient,and 0.55×10-6for the moment coef ficients.

Fig.10 Lift aerodynamic coef ficients variation versus angle of attack α.

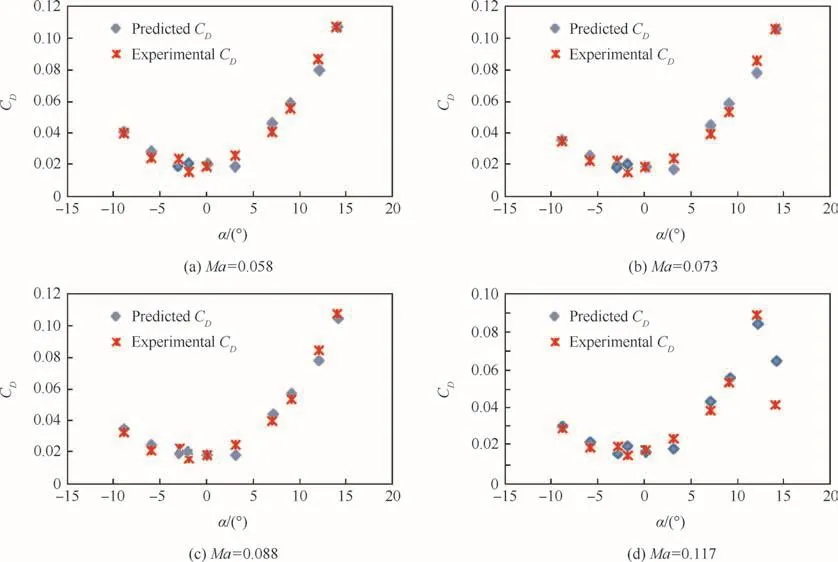
Fig.11 Drag aerodynamic coef ficients variation versus angle of attack.

Fig.12 Moment aerodynamic coef ficients variation versus angle of attack.

Table 7 The obtained mean squared errors.

Thanks are due to Professors Michael Paϊdoussis and Stuart Price for the donation of their Subsonic Blow Down Wind Tunnel to Professor Ruxandra Mihaela Botez at the LARCASE laboratory at ETS.Special thanks are dues also to Mr.Oscar Carranza Moyao and to Mrs.Odette Lacasse from ETS.This work has been funded by the Natural Sciences and Engineering Research Council of Canada(NSERC)in the frame of the Canada Research Chair for Aircraft Modeling and Simulation Technologies.

1.El Asli N.Approche hybride base´e sur les machines a`vecteurs de support et les algorithmes ge´ne´tiques pour l’estimation des couˆts de fabrication[dissereation].Montre´al,Quebec:Quebec University;2008[French].

2.Wrong BK,Vincent SL,Lam JA.Bibliography of neural network business applications research:1994–1998.Comput Oper Res2000;27(11):1045–76.

3.Hunt KJ,Sbarbaro D,Zbikowski R,Gawthrop PJ.Neural networks for control systems–A survey.Automatica1992;28(6):1083–112.

4.Udo GJ.Neural networks application in manufacturing process.Comput Ind Eng1992;23(1):97–100.

5.Wong BK,Bodnovich TA,Selvi Y.Neural network application in business:A review and analysis of the literature(1988–1995).Decis Support Syst1997;19(4):301–20.

6.Chen D,Burrel P.On the optimal structure design of multilayer feedforward neural networks for pattern recognition.Int J Pattern Recognit Artif Intell2002;6(4):375–98.

7.Nourelfath M,Nahas N.Quantized hop field networks for reliability optimization.Reliab Eng Syst Saf2003;81(2):191–6.

8.Nourelfath M,Nahas N.Arti ficial neural networks for reliability maximization under budget and weight constraints.J Qual Maintenance Eng2005;11(2):139–51.

9.Ren Y,Bai GC.New neural network response surface methods for reliability analysis.Chin J Aeronaut2011;24(1):25–31.

10.Faller WE, Schreck SJ. Neural networks: applications and opportunities in aeronautics.Prog Aerosp Sci1996;32(5):433–56.

11.Rauch HE,Kline-Schoder RJ,Adams JC,Youssef HM.Fault detection,isolation,and recon figuration for aircraft using neural networks.In:AIAA-guidance,navigation and control conference;Monterey,CA,USA.1993.p.1527–37.

12.Lu X,Hu LU,Wang G,Wu Z.Helicopter sizing based on genetic algorithm optimized neural network.Chin J Aeronaut2006;19(3):212–8.

13.Xu YM,Shuo L,Rong XM.Composite structural optimization by genetic algorithm and neural network response surface modeling.Chin J Aeronaut2005;18(4):301–16.

14.Linse DJ,Stengel RF.Identi fication of aerodynamic coef ficients using computational neural networks.J Guidance Control Dyn1993;16(6):1018–25.

15.Amin SM,Gerhart V,Rodin EY.System identi fication via arti ficial neural networks:applications to online aircraft parameter estimation.SAE Trans1997;106:1787–808.

16.Johnson MD,Rokhsak K.Using arti ficial neural network and self-organizing maps for detection of airframe icing.J Aircraft2001;38(2):224–30.

17.Aykan R.Kalman filter and neural network-based icing identi fication applied to A340 aircraft dynamics.Aircraft Eng Aerosp Technol Int J2005;77(1):23–33.

18.Napolitano MR,Kincheloe M.On-line learning neural network controllers for autopilot systems.J Guidance Control Dyn1995;33(6):1008–15.

19.Yavrucuk I,Prasad JVR,Calise A.Adaptive limit detection and avoidance for carefree manoeuvringAIAA atmospheric flight mechanics conference and exhibit;2001 August 6–9;Montreal,QC,Canada.Reston:AIAA;2001.p.4003.

20.Wallach R,de Mattos BS,da Mota GR.Aerodynamic coef ficient prediction of a general transport aircraft using neural network.In:25th international congress of the aeronautical sciences ICAS;2006 September 3–8;Hamburg,Germany.2006.p.1199–214.

21.Lunia A,Isaac KM,Chandrashekhara K,Watkins SE.Aerodynamic testing of a smart composite wing using fiber-optic strain sensing and neuralnetworks.SmartMaterStruct2000;9(6):767–73.

22.Scott RC.Active control of wind-tunnel model aeroelastic response using neural networks.J Guidance Control Dyn2000;23(6):1100–8.

23.Suresh S,Omkar SN,Mani V,Guru Prakash TN.Lift coef ficient prediction at high angle of attack using recurrent neural network.Aerosp Sci Technol2003;7(8):595–602.

24.Fei H,Zhu R,Zhou Z,Wang J.Aircraft flight parameter detection based on a neural network using multiple hot- film flow speed sensors.Smart Mater Struct2007;16(4):1239–45.

25.Peyada NK,Ghosh AK.Aircraft parameter estimation using a new filtering technique based upon a neural network and Gauss–Newton method.Aeronaut J2009;113(1142):243–52.

26.Samy I,Postlethwaite I,Gu DW.Neural-network-based flush air data sensing system demonstrated on a mini air vehicle.J Aircraft2010;47(1):18–31.

27.Xuan CZ,Chen Z,Wu P,Zhang Y,Guo W.Study of fuzzy neural network on wind velocity control of low-speed wind tunnel.IEEE international conference on electrical and control engineering;2010 June 25-27;Wuhan,China.Piscataway,NJ:IEEE Press;2010.p.2024-7.

28.Sivanandam SN,Sumathi S,Deepa SN.Introduction to fuzzy logic using MATLAB.Berlin:Springer;2007.

29.de Jesus MS,Botez RM.New identi fication method based on neural network for helicopters from flight test data.AIAA atmospheric flight mechanics conference;2009 Aug 10-13;Chicago,IL,USA.Reston:AIAA;2009.p.10-3.

30.Boe¨ly N,Botez R.New approach for the identi fication and validation of a nonlinear F/A-18 model by use of neural networks.IEEE Trans Neural Networks2010;21(11):1759–65.

31.Boe¨ly N,Botez R,Kouba G.Identi fication of a non-linear F/A-18 model by the use of fuzzy logic and neural network methods.Proc Inst Mech Eng G J Aerosp Eng2011;225(5):559–74.

32.Roudbari A,Sagha fiF.Intelligent modeling and identi fication of aircraft nonlinear flight.Chin J Aeronaut2014;27(4):759–71.

33.Ben MA,Botez R,Dao TM.New methodology for calculating flight parameters with neural network-EGD method.AIAA modeling and simulation technologies(MST)conference;2013 Aug 19-22;Boston,MA,USA.Reston:AIAA;2013.p.19-22.

34.Kouba G,Botez R,Boe¨ly N.Identi fication of F/A-18 model from flight tests using the fuzzy logic method.47th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition;2009 Jan 5-8;Orlando,USA.Reston:AIAA;2009.p.1-28.

35.Kouba G,Botez R,Boe¨ly N.Fuzzy logic method use in F/A-18 aircraft model identi fication.J Aircraft2010;47(1):10–7.

36.Grigorie TL,Botez R.Adaptive neuro-fuzzy inference systembased controllers for smart material actuator modeling.Proc Inst Mech Eng G J Aerosp Eng2009;223(6):655–68.

37.Grigorie TL,Botez R,Popov AV.Adaptive neuro-fuzzy controllers for an open-loop morphing wing system.Proc Inst Mech Eng G J Aerosp Eng2009;223(7):965–75.

38.Grigorie TL,Botez R,Popov AV,Mamou M,Me´barki Y.Application of fuzzy logic in the design and control of a morphing wing using smart material actuators.58th aeronautics conference and AGM,AERO;2011 April 26–28;Montreal,Canada;2011.

39.Grigorie TL,Botez R,Popov AV,Mamou M,Me´barki Y.An intelligent controller based fuzzy logic techniques for a morphing wing actuation system using shape memory alloy.52nd AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics and materials conference;2011 April 4–7;Denver,Colorado,USA.Reston:AIAA;2011.p.2133.

40.Grigorie TL,Botez R,Popov AV,Mamou M,Me´barki Y.A hybrid fuzzy logic proportional integral-derivative and conventional on-off controller for morphing wing actuation using shape memory alloy Part 1:Morphing system mechanisms and controller architecture design.Aeronaut J2012;116(1179):433–49.

41.Grigorie TL,Botez R,Popov AV,Mamou M,Me´barki Y.A hybrid fuzzy logic proportional integral-derivative and conventional on-off controller for morphing wing actuation using shape memory alloy Part 2:Controller implementation and validation.Aeronaut J2012;116(1179):451–65.

42.Antoine C,Laurent M,Yves K.Apprentissage arti ficiel:concepts et algorithmes.Paris:Editions Eyrolles;2002.

43.Vapnik,V.Advances in Kernel Methods Support Vector Learning.Cambridge,MA,USA:MIT Press;1999.p.25-41.

44.Kecman V.Learning and soft computing-support vector machines,neuralnetworksandfuzzylogicmodels.Cambridge,MA,USA:MIT Press;2001.

45.Smola AJ,Scholkopf B.A tutorial on support vector regression.Stat Comput2004;14(3):199–222.

46.Keerthi S.Ef ficient tuning of SVM hyper parameters using radius/margin bound and iterative algorithms.IEEE Trans Neural Networks2002;13(5):1225–9.

47.Cherkasky V,Ma Y.Practical selection of SVM parameters and noise estimation for SVM regression.Neural Networks2004;17(1):113–26.

48.Ping FP,Hong WC.Support vector machines with simulated annealing algorithms in electricity load forecasting.Energy Convers Manage2005;46(17):2669–88.

49.Dueck G.New optimization heuristics.The great deluge algorithm and the record-to-record travel.J Comput Phys1993;104(1):86–92.

50.Burke E,Bykov Y,Newell J,Petrovic S.A time-prede fined local search approach to exam timetabling problems.IIE Trans2004;36(6):509–28.

51.Ben Mosbah A,Dao TM.Optimization of group scheduling problem using the hybrid meta-heuristic extended great deluge(EGD)approach:a case study.J Manage Eng Integr2011;4(2):1–13.

52.Nahas N,Khatab A,Ait-Kadi D,Nourelfath M.Extended great deluge algorithm for the imperfect preventive maintenance optimization of multi-state systems.Reliab Eng Syst Saf2008;93(11):1658–72.

53.Ben Mosbah A.Optimisation de l’ordonnancement cellulaire avec me´taheuristiques[dissereation].Montre´al,Quebec:Quebec University;2011[French].

54.Ben MA,Dao TM.Optimization of group scheduling using simulation with the meta-heuristic Extended Great Deluge(EGD)approach.2010 IEEE international conference:Industrial engineering and engineering management(IEEM);2010 December 7-10;Macao,China.Pisscataway,NJ:IEEE Press;2010.p.275-80.

55.Ben Mosbah A,Dao TM.Optimization of manufacturing cell formation with extended great deluge meta-heuristic approach.Int J Serv Oper Inf2013;7(4):280–93.

56.Ben Mosbah A,Salinas FM,Botez R,Dao TM.New methodology for wind tunnel calibration using neural networks–EGD approach.SAE Int J Aerosp2013;6(2):761–6.

57.Ben Mosbah A,Botez R,Dao TM.New methodology for the prediction of the aerodynamic coef ficients of an ATR-42 scaled wing model.SAE 2014 aerospace systems and technology conference;2014 September 23–25;Cincinnati,OH,USA.2014.