Three-dimensional guidance law based on adaptive integral sliding mode control

Song Junhong,Song Shenmin

Center for Control Theory and Guidance Technology,Harbin Institute of Technology,Harbin 150001,China

1.Introduction

The terminal guidance law design is the basis to realize the precise guidance of missile.The aim of a terminal guidance law is to allow missiles to intercept targets with minimum miss distances.1Proportional navigation(PN)guidance law and itsvariants have been well-known guidance laws,thanks to its high ef ficiency and ease of implementation in a large variety of interception engagements.However,for the situation of intercepting the targets with a larger maneuverability,PN guidance laws are not able to intercept the targets under the required precision.2In order to deal with the maneuverable targets effectively,many researchers have developed various modern robust guidance laws based on different nonlinear control methods,such asH∞control,3L2gain control,4differential game,5sliding mode control,6–8etc.

So far,the sliding mode control(SMC)has been widely used to design controllers because of its good robustness to external disturbances and the uncertainty of the system parameters.The conventional sliding mode control,9–11whose sliding mode manifold is a linear function,can only finish the asymptotic convergence in in finite time in the sliding phase.In order to achieve the finite time convergence in the sliding phase,one of the solutions is to apply the terminal sliding mode control(TSMC)whose sliding mode manifold is a nonlinear function.12,13In addition,the TSMC can also guarantee that the convergence of the system states is faster,the convergence precision is higher and the system has a better disturbancerejection performancethan thetraditionallinear sliding mode control(LSMC).Therefore,the TSMC has been widely applied to the missile guidance law design problem.14–18Another good method is to finish the convergence in finite time by applying the integral sliding mode control(ISMC).A finite time convergent ISMC was proposed by Ref.19for a kind of higher order systems,and has been successfully used in the field about the design of the guidance law.20,21

In the implementation of the SMC,the switching gain selection is a dif ficult problem.Generally speaking,for completing the sliding mode reaching condition,we should choose the switching gain larger than the upper bound of external disturbance.So,a necessary assumption is that the disturbance has upper bound and that its upper bound needs to be known in Refs.13,17.However,in practical applications,the upper bound of external disturbance is hard to know.To resolve the abovementioned problem,the adaptive sliding mode control has been studied in much literature.22–27The advantage of the adaptive sliding mode control is that it adaptively tunes the switching gain by designing an adaptive law to estimate the value of the upper bound of the disturbance.So,we do not need to know the upper bound on the disturbance in advance.

In practice,the relative motion of target and missile takes place in the three-dimensional(3D)space,and the mathematical model that accurately describes the relation of relative motion of target and missile is complicated nonlinear strongcoupled equations.While designing the guidance law for the missile,the usual method is to decouple the 3D motion into two two-dimensional motions.There exist many researches that designed the guidance laws in the two-dimensional space.15–17,20,21However,the method based on the traditional decoupling will lose the guidance information during decoupling and result in a negative effect on terminal guidance accuracy.So,it would be close to reality if the terminal 3D guidance law is developed under the condition of not neglecting the couple among the channels of nonlinear dynamics of target-missile relative movement in the 3D space.

At present,many 3D guidance laws have been developed.For example,a few 3D PN guidance laws were developed in Refs.28–30.However,for intercepting a strong maneuvering target,the robustness of such guidance laws is not so well.Based on a geometric method,a 3D guidance law considering angle constraints was developed for the non-maneuvering targets in Ref.31.In Refs.32,33,a 3D guidance law was proposed for maneuvering targets based on a nonlinear backstepping control approach.Note that in Refs.32,33,the guidance laws were designed for maneuvering targets,but the proposed guidance laws could not guarantee that the system states converge in finite time.Then,in Refs.34,35,SMC-based 3D guidance laws considering impact angle constraints were proposed.However,in Ref.34,the guidance law was designed for stationary targets.Although the guidance law was proposed for maneuvering targets in Ref.35,the information of the target acceleration bound needs to be known in advance.Hence,for the guidance problem in the terminal phase when the missiles intercept the high-speed maneuvering targets,to study the finite time convergent 3D guidance law without any information about the upper bound of the target acceleration is not only theoretically challenging but also practical requirement.

For the guidance problem in the terminal phase when the missiles intercept the high-speed maneuvering targets,the main contribution of this paper is to develop a non-decoupling and finite time convergent 3D guidance law and without the knowledge of the bound on the target acceleration in advance.First of all,based on the ISMC,a new 3D integral sliding mode(ISM)guidance law is put forward in the 3D environment,which can guarantee the finite time convergence of guidance system states.Then,a novel 3D adaptive integral sliding mode(AISM)guidance law with the finite time convergence is proposed by combination of the ISMC and adaptive control technique which is used to estimate the unknown upper bound of the target acceleration.

2.Formulation of guidance model

In this section,the target-missile relative motion equations for the 3D guidance system are presented.Fig.1 shows the 3D interception geometry.T denotes the target,M the missile,Oxyza inertial reference frame,Ox1y1z1a line-of-sight(LOS)frame andRthe relative distance between the target and missile;qεandqβare the elevation and azimuth angles of the LOS,respectively.

Regard the missile and the target as point mass in designing guidance laws and the velocities of the missile and the target;VMandVT,are assumed to be constants.3D relative motion geometry of missile and target,as given in Fig.1,can be expressed by the following differential equations17:

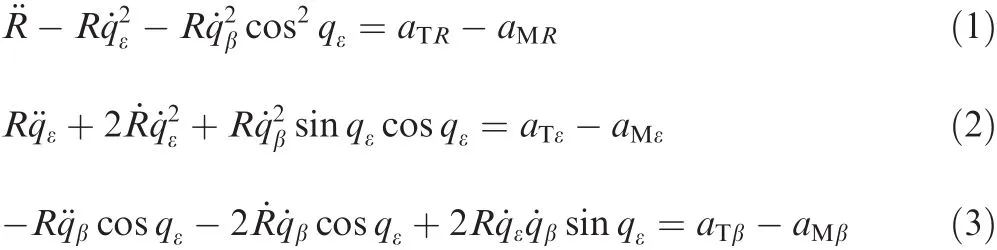
From Eqs.(2)and(3),it can be obtained that there exist serious cross couplings between the elevation and the azimuth channels of the LOS.

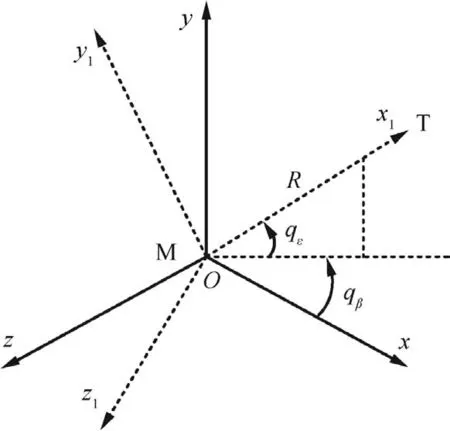
Fig.1 Three-dimensional interception geometry.

In many practical terminal guidance processes,there are no thrusts,and then the magnitude of the missile’s velocity is generally uncontrollable.Hence,we do not consideraMRas the control variable,but the missile normal accelerations,aMεandaMβ,are regarded as control variables to change the direction of missile’s velocity.In designing guidance laws,we just need to make the LOS angular rates,˙qεand˙qβ,converge to zero by designing the control variablesaMεandaMβwhen the relative velocity of the missile-target is less than zero.Therefore,in the design process of the guidance law,the objective is to make the LOS angular rates˙qεand˙qβconverge to zero,and then Eq.(1)can be omitted.

De finingx1=qε,x2=˙qε,x3=qβ,x4=˙qβand combining Eqs.(2)and(3)yield the three-dimensional guidance system described as follows:

In practical applications,the target’s acceleration is viewed as external disturbance and it is not easy to obtain.But the target’s acceleration is usually bounded.Hence,we have the following assumption.

Assumption 1.Suppose thatand ε2are positive constants.

3.Guidance law design

Before designing the guidance laws,we first give some lemmas which are used to verify the stability of the guidance system.

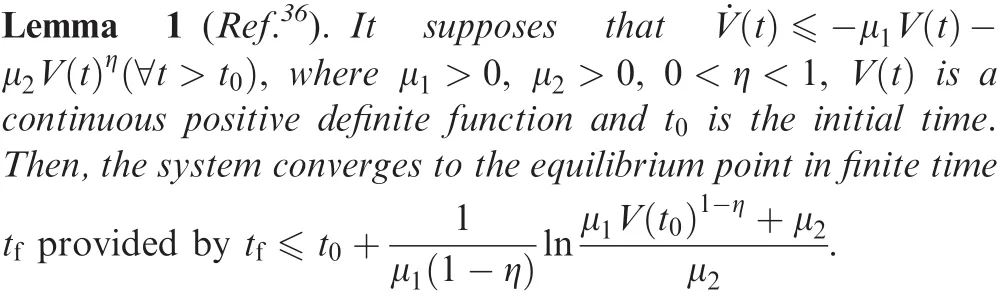
3.1.Integral sliding mode guidance law design

In this subsection,a novel nonlinear ISM guidance law is presented to ensure the disturbance rejection performance of the three-dimensional guidance system described by Eq.(4).A brief design process of the developed ISM guidance law is given as follows.Firstly,we design a nonlinear integral sliding surface vector.Secondly,on the basis of the nonlinear integral sliding surface vector,a nonlinear ISM guidance law is proposed.Then,it is obtained that under the developed guidance law,the LOS angular rates,˙qεand˙qβ,converge to zero in finite time in the presence of the external disturbances whose upper bound can be known.

Inspired by Ref.20,a sliding surface vector is chosen as

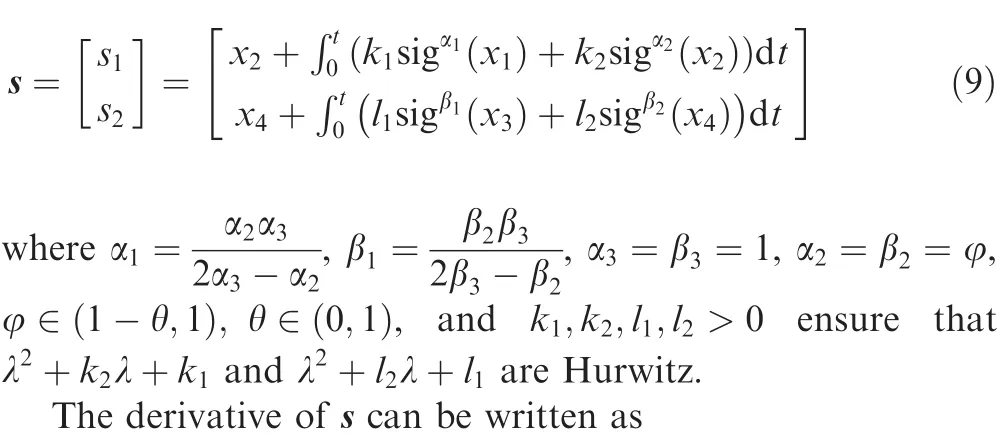
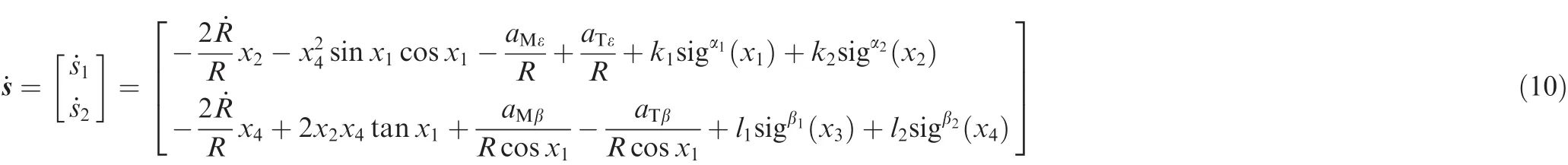
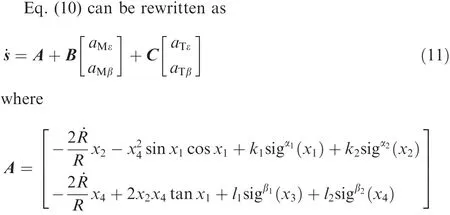
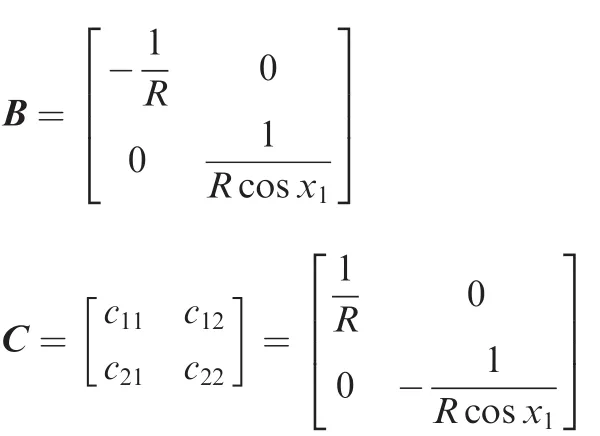
Because the seeker has a minimum action distanceR0,we haveR≥R0during the guided flight process of the missile,thus B is nonsingular providedx1remains small.Based on the integral sliding surface vector Eq.(9),we proposed the following the ISM guidance law for the guidance system Eq.(4).

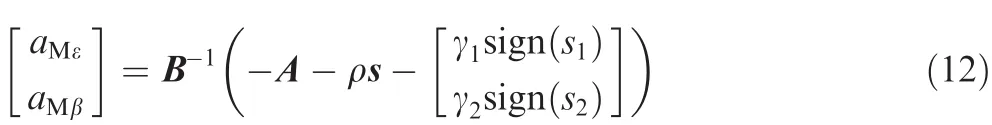
where γi≥ ωi+ ε1|ci1|+ ε2|ci2|,ωi＞ 0(i=1，2)is a constant.And ρ is a positive constant.

Then,the first theorem is given as follows.

Based on Lemma 1,the sliding surface vector converges to zero in finite time,i.e.si（t1）=0 （i=1，2）,wheret1is the time of sliding surface vector converging to zero.Then,for allt≥t1, we havesi=0 （i=1，2）, which implies that ˙si=0（i=1，2）,i.e.

According to Lemma 2,x2andx4can converge to zero in finite time,i.e.q˙εandq˙βconverge to zero in finite time,respectively.The proof of Theorem 1 is completed.□

Remark 1.As clearly seen in the designed guidance law Eq.(12),the implementation of the designed ISM guidance law depends on the upper bound of the target’s acceleration.However,in many practical situations,there is no accurate knowledge about the upper bounds of the target acceleration.To overcome the problem,the adaptive control scheme is a good choice.So,a new AISM guidance law will be developed in the following subsection.

3.2.Adaptive integral sliding mode guidance law design

In the subsection,an adaptive law is proposed which is used to estimate the upper bound of the target’s acceleration online.With the help of the adaptive law,an novel robust AISM guidance law is proposed for the 3D guidance system Eq.(4)which needs not to know the upper bound of the target’s acceleration in advance.The design method on the novel AISM guidance law is similar to that of the previously mentioned integral sliding mode guidance law.And the developed AISM guidance law can guarantee that the LOS angular rates˙qεand˙qβconverge to zero in finite time without the information on the upper bound of the target’s acceleration.Then,the following theorem is obtained.

Theorem 2.For the guidance system Eq.(4)with the sliding surface vector Eq.(9),the LOS angular rates˙qεand˙qβwill converge to zero in finite time under the following guidance law Eq.(19)and the designed adaptive laws Eq.(20).

Computing the first order derivative ofV2along system Eq.(11)and using Eqs.(19)and(20),we have

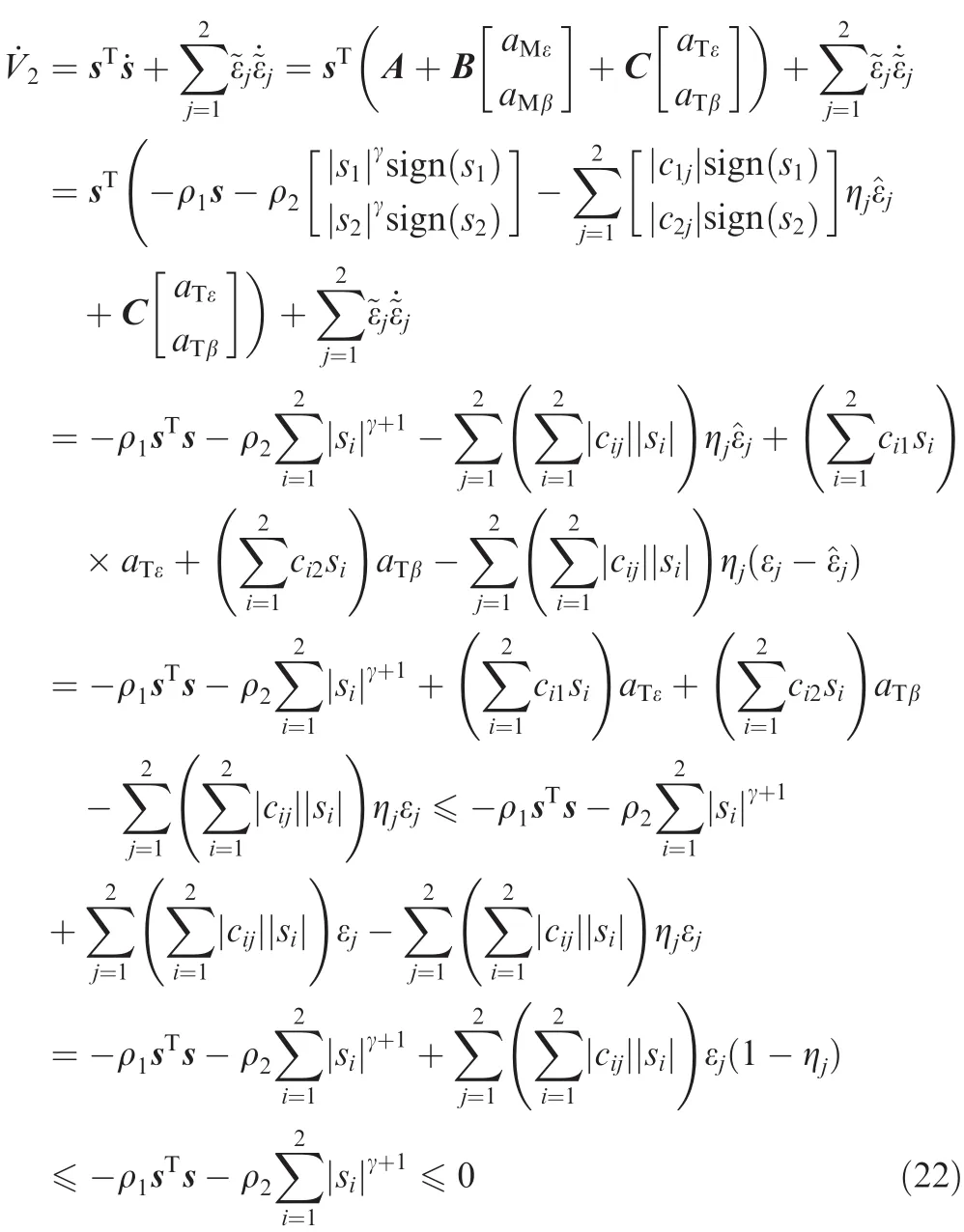
From the inequality(22),we can obtainV2（t）≤V2（0）,which implies thatV2（t）is bounded.Hence,it can be concluded that s and（j=1，2）are all bounded.

Furthermore,consider another Lyapunov function

Applying Eqs.(19)and(20),the derivative ofV3can be written as

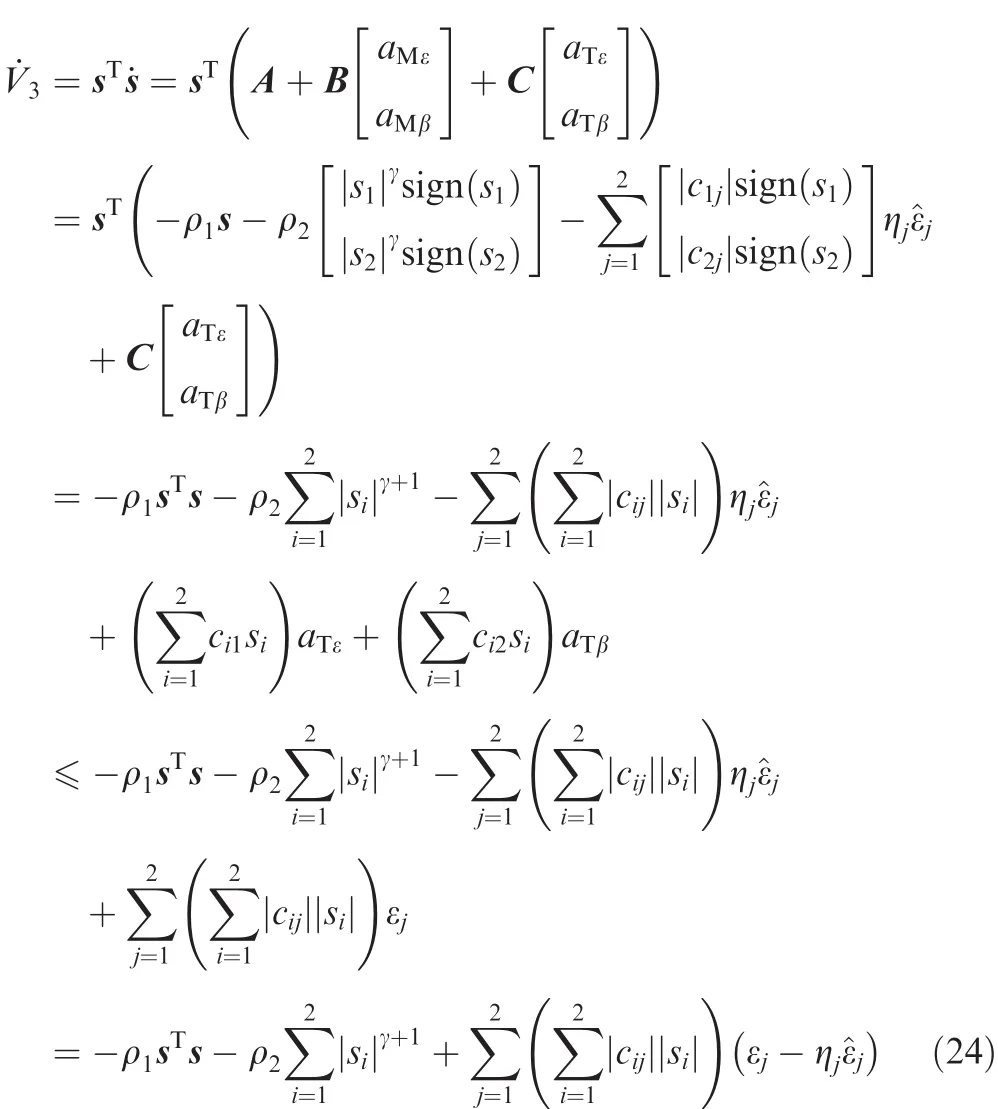
Based on Lemma 1,the sliding surface vector converges to zero in finite time.The remaining steps of the proof are similar to those of Theorem1.Hence,the remaining steps are omitted here.So,conclusions can be easily obtained that the LOS angular rates˙qεand˙qβconverge to zero in finite time,respectively.The proof of Theorem 2 is completed.□

Remark 2.Compared with Theorem 1,an adaptive estimation term is introduced into the guidance law Eq.(19)in Theorem 2.From the guidance law Eq.(19),it is easy to see that the proposed AISM guidance law Eq.(19)does not contain the information on the upper bounds of the target’s acceleration.Instead,the upper bound is provided by applying the adaptive law Eq.(20)to estimate the bound.Thus,the AISM guidance law Eq.(19)successfully resolves the mentioned problem existing in the ISM guidance law Eq.(12).

Note that the ISM guidance law Eq.(12)and the AISM guidance law Eq.(19)are discontinuous controller because of the existing of signum function which can bring about the undesirable chattering problem.To alleviate the chattering,a continuous saturation function sat（y）given in Eq.(29),which is used to approximate the signum function,takes place of the signum function.

wherehis a small positive constant.Ifhis given smaller enough,then better approximating effect will be obtained.

So,the corresponding ISM guidance law in Eq.(12)and the AISM guidance law in Eq.(19)can be modi fied as

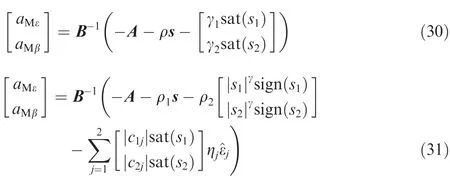
4.Simulation

To illustrate the effectiveness of the designed guidance laws Eqs.(30)and(31)in the above section,this section shows the numerical simulations for the missiles air-intercepting the maneuvering targets at constant speed and time-varying speed.

The simulation parameters are missile parameters and target parameters.The missile parameters are given by:(1)initial position coordinates:xM（0）=0 m,yM（0）=0 m andzM（0）=0 m;(2)velocity:VM=1000 m/s;(3)initial flight path angle and heading angle: θM（0）=45°and φM（0）=0°.The target parameters are given by:(1)initial position coordinates:xT（0）=11136 m,yT（0）=8603.6 m andzT（0）=5192.8 m;(2)velocity:VT=800 m/s;(3)initial flight path angle and heading angle:θT（0）=-30°and φT（0）=120°.

The parameters of the ISM guidance law Eq.(30)are given as follows:parameters of the AISM guidance law Eq.(31)are chosen as:40，ρ1=5，ρ2=1，γ=0.5, η1= η2=10,h=0.002.The maximum normal accelerations that missile can provide perpendicular to the LOS are assumed to be 25grespectively,andgis the acceleration of gravity(g=9.8m/s2).

4.1.Constant speed missiles

In the subsection,for the constant speed missiles intercepting three different kinds of targets,the simulation examples are provided to illustrate the guidance performance of both designed guidance laws.

For performance comparison,the augmented proportional navigation(APN)guidance law is also simulated under the same initial conditions.The APN guidance law is chosen as

where the parameterNis set to be 4.

To verify the effectiveness of the designed guidance laws,the following three cases for the different target acceleration are selected as follows:

Case 1.aTε=7gsint and aTβ=7gcost.

Case 2.aTε=7g and aTβ=7g.

Case 3.aTεand aTβare squares with an amplitude of 7g,a period of 4 s and a phase delay of 0.1 s.

With the given initial conditions and data,simulations are performed for the three cases under all the three guidance laws.For the three cases,Figs.2–4 show the simulation results.Each if gure includes the response of the elevation angular rate of the LOSthe azimuth angular rate of the LOSthe sliding mode manifoldss1ands2,the missile acceleration in the elevation loopaMε,the missile acceleration in the azimuth loopaMβ,the estimation error of the upper bound of target acceleration（j=1，2）,and the relative movement curve of the missiletarget for all the three guidance laws,which are given in Figs.2(a)–(h),3(a)–(h),4(a)–(h),respectively.The abbreviations in Figs.2–4 and Table 1,i.e.ISMGL,AISMGL and APNGL,denote the proposed integral sliding mode guidance law Eq.(30),adaptive integral sliding mode guidance law Eq.(31)and the augmented PN guidance law Eq.(32),respectively.Table 1 presents the miss distances and interception times.

From the Figs.2(a),3(a),4(a)and 2(b),3(b),4(b),it can be obtained that both proposed guidance laws can ensure that the LOS angular rates˙qεand˙qβconverge to zero in finite time for the target acceleration pro files of Cases 1–3.However,the convergence property of the LOS angular rates˙qεand˙qβunder the APNGL is not the same for the three cases.For Case 1 and Case 2,the LOS angular rates˙qεand˙qβdo not converge to zero.For Case 3,if the target is a square maneuvering,the APNGL can guarantee that the LOS angular rates˙qεand˙qβconverge to zero,but the LOS angular rates˙qεand˙qβdiverge at an early time which leads to a large miss distance.As shown in Figs.2(c),3(c),4(c)and 2(d),3(d),4(d),it can also be seen that both variables of the sliding surface vector converge to zero rapidly in finite time under both proposed guidance laws for the three cases.From these figures,we can also observer that the sliding surface variable curves are smooth and stable even for the case of square maneuvering target.As presented in Figs.2(e),3(e),4(e)and 2(f),3(f),4(f),the missile accelerations in the two loops under both proposed guidance laws are within the reasonable bounds and there are problems of acceleration saturations in the initial phase of the terminal guidance process for all target acceleration cases.And,the missile accelerations produced by the APNGL are much smaller than those under the ISMGL and AISMGL.But,the larger missile acceleration taken by the proposed ISMGL and AISMGL can make the LOS angular rate preferably converge to zero in finite time and large acceleration decreases correspondingly as the LOS angular rates come close to zero.In addition,we can see that with the convergence properties of the LOS angular rates,the missile acceleration commands under the proposed guidance laws converge to the similar curve with the target’s acceleration for each case after a while.From Figs.2(g),3(g),4(g),we can observer that the estimation error of the upper bound of the target’s acceleration rapidly converge to zero under the proposed AISMGL for the three cases,which indicates that the designed adaptive law can effectively estimate the upper bound of the target’s acceleration.It can be clearly observed from Figs.2(h),3(h),4(h)that with the implementation of both developed ISMGL and AISMGL,the missile can intercept the target successfully for all the target acceleration pro files of Cases 1–3.The relative movement curves of the missile-target under the proposed AISMGL are similar to that under APNGL for any case.And the proposed ISMGL makes the missiles have slightly longer trajectories than those of the other guidance laws for the three cases.

Fig.2 Response curves under three guidance laws of Case 1.

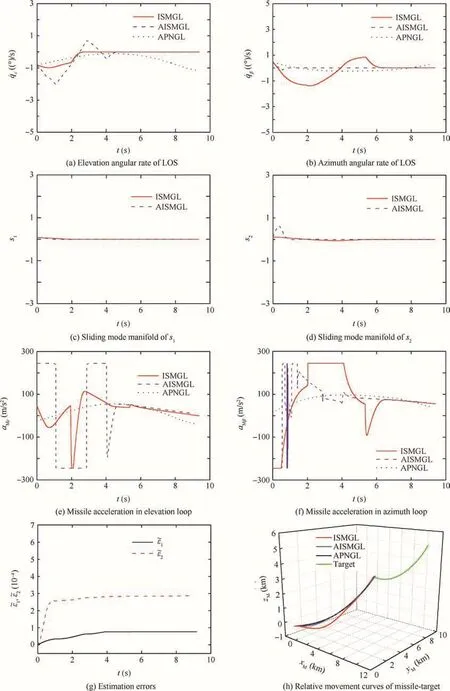
Fig.3 Response curves under three guidance laws of Case 2.

Fig.4 Response curves under three guidance laws of Case 3.

Table 1 Miss distances and interception times for three cases.

From Table 1,it can be observed that the interception time under both designed guidance laws is similar to that under the APNGL for the Cases 1–3.But,by comparing the miss distance for all the target cases,the miss distances achieved by the proposed ISMGL and the AISMGL are much less than the APNGL.So,the APNGL cannot ensure the guidance accuracy,while the proposed ISMGL and AISMGL can ensure that the missile intercepts the target successfully and have a high guidance precision even in the case of existing strong target maneuver.

4.2.Varying speed missiles

In Section 4.1,only the simulation results for the constant speed missiles are shown.Nonetheless,as we all know,the speed of the missile for a realistic missile model15is variable,hence,the following simulation results are presented to demonstrate the effectiveness of the above designed guidance laws for missiles with varying speed which is as good as that for the constant speed missiles.This is due to the inherently strong robustness of the designed guidance laws.The equations of motion of a missile,which is regarded as a pointmass flying over a flat,non-rotating Earth,are described as follows:

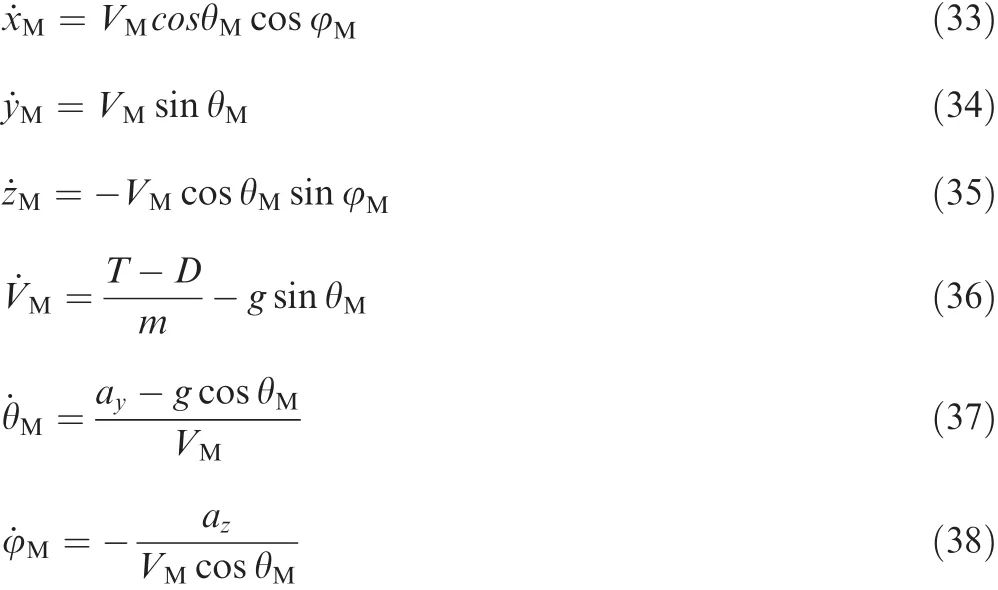
wherexM，yMandzMdenote the position of the missile;m，θMand φMrepresent the mass,the flight path angle and the heading angle of the missile,respectively;TandDdenote the thrust and the drag of the missile,respectively;ayandazare the horizontal projection and vertical projection of the missile normal acceleration.

For the realistic missile model,the expression of the aerodynamic dragDin Eq.(36)is given as

whereD0andDiare the zero-lift drag and induced drag;CD0andKdenote the coef ficient of the zero-lift drag and the coefficient of the induced drag;Q，Ar，eand ρ represent the dynamic pressure,the aspect ratio,the ef ficiency factor and the atmosphere density,respectively;andsis the reference area and assumed to be 1 m2.For the guidance problem,CD0andKare given as

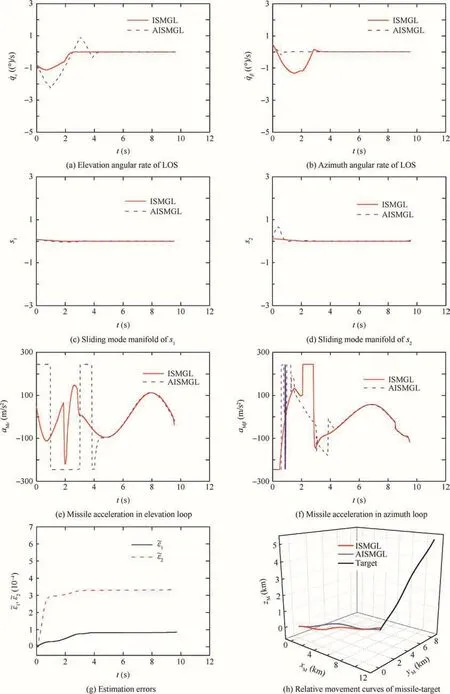
Fig.5 Response curves with the proposed ISMGL and AISMGL.

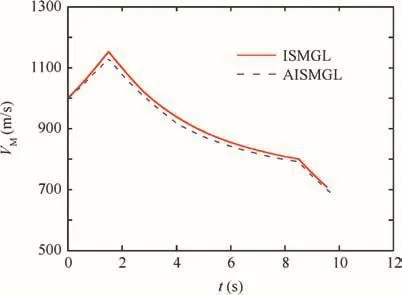
Fig.6 Variations of missile speed with the proposed ISMGL and AISMGL.

The simulation conditions are the same as the previous simulation and the target acceleration is chosen asaTε=7gsint,aTβ=7gcostwhich is the same as Case 1.The missile’s initial speed and the target’s initial speed are 1000 m/s and 800 m/s,respectively.With the implement of the proposed ISMGL and AISMGL,the LOS angular rates˙qεand˙qβ,the sliding mode manifolds1ands2,the missile acceleration in the elevation loopaMε,the missile acceleration in the azimuth loopaMβ,the estimation error of the upper bound of target acceleration（j=1，2）,the relative movement curve of the missile-target,and the variation of the missile speed are given in Figs.5 and 6.In addition,we can also obtain that under the ISMGL and AISMGL,the miss distances are 0.020 m and 0.015 m,and the intercepting times are 9.550 s and 9.690 s,respectively.From Fig.5,we can observer that under both designed guidance laws,the simulation results for the varying speed missile are similar to the results of Case 1 for the constant speed missile in the above subsection,respectively.Fig.6 shows the variation of the missile speed for the ISM guidance law and AISM guidance law.As shown in Fig.6,it can be observed that it can be observed that the speed of the missile fast increases at the start of the engagement owing to the larger thrust compared with the drag.Then,after the second,the speed of the missile decreases when the thrust is less than the drag on the missile.As the missile speed decreases,the interception time for varying speed missiles is a little longer than that for constant speed missiles under both proposed guidance laws.Therefore,it can be concluded that the performances of the developed guidance laws for the time-varying speed missiles are as good as those for the constant speed missiles.

5.Conclusions

In this paper,for the guidance problem in the terminal phase when the missiles intercept the high-speed maneuvering targets in the 3D space,the finite-time guidance law design is studied.The main contributions of this work are listed as follows:

(1)A new 3D ISM guidance law based on a finite time convergence of the integral sliding mode manifold is proposed.The proposed ISM guidance law depends on the information on the upper bound of the target’s acceleration.Therefore,with the novel use of the adaptive control,an improved AISM guidance law which does not need the upper bound of the target’s acceleration is proposed.

(2)With the aid of the Lyapunov stability theory,we obtain that the 3D guidance system is finite-time stable.It is proved that the elevation angular rate of the LOS and the azimuth angular rate of the LOS converge to zero in finite time for both developed guidance laws.

(3)Numerical simulation results including the constant speed and the varying speed missile intercepting the maneuvering target have shown the effectiveness and high-precision guidance performance of both proposed guidance laws.

In this paper,we research the finite-time guidance law design;however we did not consider the input saturation problem.At present,only a few papers focus on the finite-time guidance law design problem under input saturation.Under the input saturation,how to develop the finite-time guidance law which can produce higher guidance precision and better robustness is a challenging task,which is also our research direction.

Acknowledgements

The authors acknowledge the financial support provided by the National Natural Science Foundation of China(Nos.61174037 and 61021002)and the Aeronautical Science Foundation of China(No.20140177002).

1.Rogers S.Missile guidance comparison.Proceeding of AIAA guidance,navigation,and control conference;2004 Aug 16–19;Rhode Island.Reston:AIAA;2004.

2.Zhou D,Sun S,Teo KL.Guidance laws with finite time convergence.J Guid Control Dyn2009;32(6):1838–46.

3.Yang CD,Chen HY.NonlinearH∞robust guidance law for homing missiles.J Guid Control Dyn1998;21(6):882–90.

4.Zhou D,Mu CD,Shen TL.Robust guidance law withL2gain performance.Trans Jpn Soc Aeronaut Space Sci2001;44(144):82–8.

5.Oshman Y,Arad D.Differential-game-based guidance law using target orientation observations.IEEE Trans Aerosp Electron Syst2006;42(1):316–26.

6.Harl N,Balakrishnan SN.Impact time and angle guidance with sliding mode control.IEEE Trans Control Syst Technol2012;20(6):1436–49.

7.Yamasaki T,Balakrishnan SN,Takano H,Yamaguchi I.Second order sliding mode-based intercept guidance with uncertainty and disturbance compensation.Proceeding of AIAA guidance,navigation,and control conference;2013 Aug 19–22;Boston,MA.Reston:AIAA;2013.

8.Sha fiei MH,Binazadeh T.Application of partial sliding mode in guidance problem.ISA Trans2013;52(2):192–7.

9.Shtessel YB,Shkolnikov IA,Levant A.Guidance and control of missile interceptor using second-order sliding modes.IEEE Trans Aerosp Electron Syst2009;45(1):110–24.

10.Xia YQ,Zhu Z,Fu MY.Back-stepping sliding mode control for missile system based on an extended state observer.IET Control Theory Appl2009;5(1):93–102.

11.Brierley SD,Longchamp R.Application of sliding-mode control to air-air interception problem.IEEE Trans Aerosp Electron Syst1990;26(2):306–25.

12.Man Z,Paplinski AP,Wu HR.Arobust MIMO terminal sliding mode control scheme for rigid robotic manipulators.IEEE Trans Autom Control1994;39(12):2464–9.

13.Feng Y,Yu XH,Man ZH.Non-singular terminal sliding mode control of rigid manipulators.Automatica2002;38(12):2159–67.

14.Kumar SR,Rao S,Ghose D.Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints.J Guid Control Dyn2012;35(4):1230–46.

15.Kumar SR,Rao S,Ghose D.Nonsingular terminal sliding mode guidance with impact angle constraints.J Guid Control Dyn2014;37(4):1114–30.

16.Zhang YX,Sun MW,Chen ZQ.Finite-time convergent guidance law with impact angle constraint based on sliding-mode control.Nonlinear Dyn2012;70(1):619–25.

17.Sun S,Zhou D,Hou WT.A guidance law with finite time convergence accounting for autopilot lag.Aerosp Sci Technol2013;25(1):132–7.

18.Xiong SF,Wang WH,Liu XD,Wang S,Chen ZQ.Guidance law against maneuvering targets with intercept angle constraint.ISA Trans2014;53(4):1332–42.

19.Zong Q,Zhao ZS,Zhang J.Higher order sliding mode control with self-tuning law based on integral sliding mode.IET Control Theory Appl2010;4(7):1282–9.

20.Zhang ZX,Li SH,Luo S.Composite guidance laws based on sliding mode control with impact angle constraint and autopilot lag.Trans Inst Meas Control2013;35(6):764–76.

21.Zhang ZX,Li SH,Luo S.Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint.Aerosp Sci Technol2013;31(1):30–41.

22.Huang YJ,Kuo TC,Chang SH.Adaptive sliding-mode control for nonlinear systems with uncertain parameters.IEEE Trans Syst Man Cybern2008;38(2):534–9.

23.Lu P,Doman DB,Schierman JD.Adaptive terminal guidance for hypervelocity impact in speci fied direction.J Guid Control Dyn2006;29(2):269–78.

24.Atir R,Hexner G,Weiss H,Shima T.Target maneuver adaptive guidance law for a bounded acceleration missile.J Guid Control Dyn2010;33(3):695–706.

25.He SM,Lin DF.Adaptive nonsingular sliding mode based guidance law with terminal angular constraint.Int J Aeronaut Space Sci2014;15(2):146–52.

26.Komurcugil H.Adaptive terminal sliding-mode control strategy for DC–DC buck converters.ISA Trans2012;51(6):673–81.

27.Mondal S,Mahanta C.A fast converging robust controller using adaptive second order sliding mode.ISA Trans2012;51(6):713–21.

28.Yang CD,Yang CC.Analytical solution of 3D true proportional navigation.IEEE Trans Aerosp Electron Syst1996;32(4):1509–22.

29.Oh JH,Ha IJ.Capturability of the 3-dimensional pure PNG law.IEEE Trans Aerosp Electron Syst1999;35(2):491–503.

30.Tyan F.Uni fied approach to missile guidance laws:A 3D extension.IEEE Trans Aerosp Electron Syst2005;41(4):1178–99.

31.Yoon MG.Relative circular navigation guidance for threedimensionalimpactanglecontrolproblem.JAerospEng2010;23(4):300–8.

32.Lei W,Li S,Zhao Y.Design of anti-ship missile’s terminal guidance law with multiple constraint based on backstepping.Proceedings of the 2nd IEEE conference on instrumentation,measurement,computer,communication and control;2012 Dec 8–10;Harbin,China.Piscataway,NJ:IEEE Press;2012.p.892–5.

33.Zhang J,Cao Y,Song X,Zhang M,Shen G.3D guidance for vertical impact on non-stationary targets.Proceedings of IEEE internationalconferenceonautomationandlogistics;2012 Aug 15-17;Zhengzhou,China.Piscataway,NJ:IEEE Press;2012.p.272-6.

34.Kumar SR,Ghose D.Three dimensional impact angle constrained guidance law using sliding mode control.Proceedings of IEEE American control conference;2014 Jun 4-6;Portland,Oregen.Piscataway,NJ:IEEE Press;2012.p.2474-9.

35.Gu WJ,Yu JY,Zhang RC.A three-dimensional missile guidance law with angle constraint based on sliding mode control.Proceedings of IEEE international conference on control and automation;Piscataway,NJ:IEEE Press;2007.p.299-302.

36.Yu SH,Yu XH,Shirinzadeh B,Man ZH.Continuous finite-time control for robotic manipulators with terminal sliding mode.Automatica2005;41(11):1957–64.

37.Bhat S,Bernstein D.Geometric homogeneity with applications to finite time stability.Math Control Signals Syst2005;17(2):101–27.38.Hardy H,Littlewood JE,Polya G.Inequalities.Cambridge:Cambridage University Press;1952.