Nonlinear thermomechanical deformation behaviour of P-FGM shallow spherical shell panel

Vishesh Ranjan Kar,Subrata Kumar Panda

Department of Mechanical Engineering,National Institute of Technology,Rourkela 769008,India

1.Introduction

Functionally graded materials(FGMs)are the advanced class of composite while the constituents are graded in one or more direction with continuous variation to achieve the desired properties.The smooth grading of constituents result in better thermal properties,higher fracture toughness,improved residual stress distribution and the reduced stress intensity factors.1The above-discussed characteristics allow FGM structures to withstand large mechanical load under elevated thermal environment.Hence,the analysis of FGM structures through the mathematical model by taking one and all the complexities into the consideration are the major concern of the researchers.It is also true that experimental analysis of such complex problems is not only costly but also tough to achieve.Some of the important contributions on the linear and nonlinear de flection behaviour of FGM flat/curved panels under thermal and/or mechanical load are discussed in the following lines.

Nonlinear bending and the post-buckling responses of functionally graded(FG)plate are analysed by Yang and Shen,2using perturbation technique and 1-D differential quadrature approximation based on the classical plate theory(CPT)and von Karman nonlinearkinematics.In the continuation towards improvement,the static and dynamic behaviour of the FG flat/curved panel have been analysed using first-order shear deformation theory(FSDT).3–5Navazi and Haddadpour6reported exact solution of nonlinear bending responses of FG plate using the FSDT mid-plane kinematics and von Karman nonlinearity.In order to achieve the parabolic transverse shear through the thickness of the FG plate,7the mid-plane kinematics of the plate structure is evaluated using higher-order shear deformation theory(HSDT).Abdelaziz et al.8proposed new higher-order theory to obtain the bending response of FG sandwich rectangular plate.Upadhyay and Shukla9examined the nonlinear static and dynamic behaviour of FG skew plate using von Karman type nonlinear kinematics in the framework of the HSDT.Oktem et al.10examined the bending behaviour of flat and doubly curved FG panel in the framework of the HSDT mid-plane kinematics.Thai and Choi11developed a re fined plate theory to analyse the static,vibration and buckling behaviour of FG plate resting on elastic foundation.Bourada et al.12developed a re fined trigonometric higher-order beam theory to examine the vibration and the bending behaviour of FG beams.Yahia et al.13employed different higher-order shear deformation plate theories for wave propagation in FG plates.Meziane et al.14presented an ef ficient re fined shear deformation theory to investigate the vibration and the buckling behaviour of exponentially graded sandwich plate resting on elastic foundation under different support conditions.Belabed et al.15employed an ef ficient and simple higher-order shear and normal deformation theory to study the bending and the free vibration behaviour of FGM plate.Draiche et al.16examine the free vibration behaviour of laminated plate with a localized patch mass using trigonometric four variable plate theory.Bousahla et al.17proposed a new trigonometric higher-order theory including the stretching effect to examine the static responses of FG plates.Hebali et al.18developed a new quasi-three-dimensional hyperbolic shear deformation theory to analyse the bending and the free vibration analysis of FG plates.Larbi et al.19developed an ef ficient shear deformation beam theory based on neutral surface position to examine the bending and the free vibration of FG beams.Few more layered/graded/sandwich type structures are analysed using higher-order shell theories for the computation of realistic responses.20–23

It is well known that the FG structures are well suited to elevated thermal environment and very few numerical and/or analytical thermoelastic analysis of FG flat/curved panels are reported in the open literature.Woo and Meguid24studied the nonlinear bending of flat and spherical FG panel under combined thermo-mechanical loading based on the CPT kinematics and von Karman nonlinearity.The linear and nonlinearstaticresponsesarecomputed forFG shellpanel subjected to thermomechanical loading in the framework of Sander’s FSDT kinematics with the advent of mesh-free kp-Ritz method.25,26The analytical/numerical nonlinear solutions for FG plate under combined thermomechanical load have been investigated using HSDT kinematics with von Karman nonlinearity.27–29Wattanasakulpong et al.30employed an improved HSDT mid-plane kinematics to examine the free and forced vibration behaviour of FG plate under thermal environment.The nonlinear flexural and stability responses of FG spherical shell panels under thermomechanical load are solved analytically.31,32Na and Kim33investigated the nonlinear bending responses of FG plate under different thermal environment using 3D finite element method(FEM).Zidi et al.34employed a four variable re fined plate theory to study the bending of FGM plate resting on elastic foundation and subjected to hygro-thermo-mechanical load.Tounsi et al.35proposed a re fined trigonometric shear deformation theory with the transverse shear deformation effect for bending analysis of FG sandwich plates under thermomechanical load.Bouderba et al.36presented the thermomechanical bending of FG plates resting on Winkler–Pasternak elastic foundations using the re fined trigonometric shear deformation theory.Khal fiet al.37examined thermal buckling of solar FG plate resting on two-parameter Pasternak’s foundations using a re fined and simple shear deformation theory.Attia et al.38employed different re fined plate theories to examine the vibration behaviour of temperature-dependent FG plates.Hamidi et al.39studied the bending analysis of FG sandwich plates subjected to thermomechanical loading using a sinusoidal plate theory.Houari et al.40developed a new higher-order shear and normal deformation theory to examine the bending behaviour of FGM sandwich plates under thermomechanical load.

It is clear from the above review that the studies related to the nonlinear bending analysis of the FG flat/curved panel are very few in numbers.We note that most studies are presented on the linear flexural analysis without considering the temperature effect.Based on the authors’knowledge,no study has been reported yet in open literature on the nonlinear bending analysis of power-law based FGM(P-FGM)spherical shell panel by considering Green-Lagrange type geometrical nonlinearity and the HSDT mid-plane kinematics with/without temperature-dependent material properties.In addition to the above,all the nonlinear higher-order terms are included in the present mathematical formulation to compute the exact flexural responses.Hence,in this present work,authors’aim to develop a general nonlinear mathematical model of P-FGM shallow shell panel with temperature-dependent properties of each constituent(ceramic and metal)in the framework of the HSDT mid-plane kinematics and Green-Lagrange type full nonlinearity.In this study,the P-FGM shell panel properties are computed using Voigt’s micromechanical model and the desired nonlinear governing equation is developed through variational approach.The domain has been discretised using suitable finite element steps and a direct iterative method is introduced to compute the desired nonlinear solution.Wide varieties of numerical examples are exempli fied to highlight the effect of different geometrical and material parameters on the linear and nonlinear thermomechanical responses of the P-FGM shallow spherical shell panel.

2.Mathematical formulations

2.1.Kinematic model for shallow spherical shell panel

For the analysis purpose,a shallow spherical shell panel with a rectangular base(a×b)is developed mathematically in Cartesian coordinates(x–y–z)as shown in Fig.1.Here,his the total panel thickness and,RxandRyare the radii of curvature of mid-plane alongx-andy-axis,respectively.The displacement field of the present P-FGM spherical shell panel is de fined in the HSDT mid-plane kinematics41as

where(u,v,w)is the global displacement field and(u0,v0,w0)is the mid-plane displacement field alongx,yandzdirections,respectively. θxand θyare the rotations of transverse normal abouty-andx-axes,respectively.are the mid-plane higher-order terms of Taylor’s series expansion.

2.2.Strain–displacement relationships

The small strain and large deformation behaviour of any material continuum can be expressed as Green-Lagrange type nonlinear strain–displacement relation as42

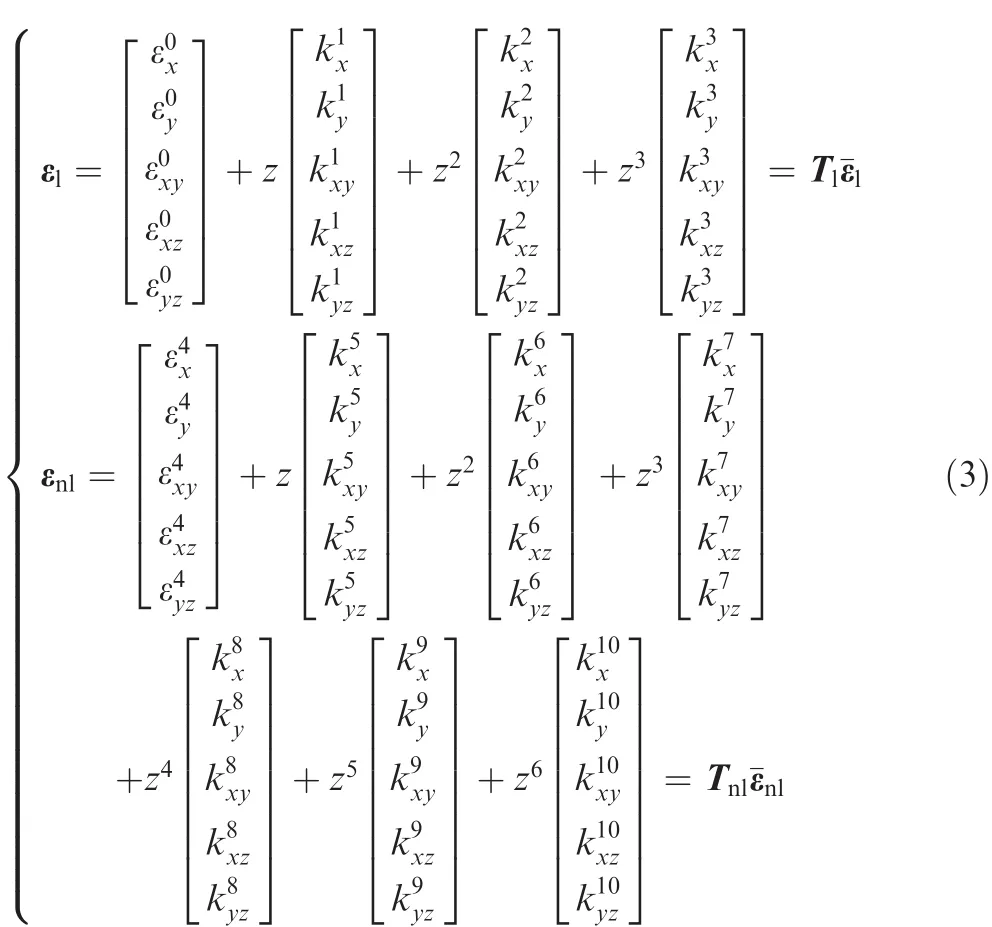
where the individual terms and the details can be seen in Ref.43.Similarly,Tland Tnlrepresent the linear and the nonlinear thickness coordinate matrices,respectively.

Fig.1 Geometrical details of shallow spherical P-FGM shell panel.

2.3.Material gradation and property evaluation

In general,the FGM is composed of the metal and ceramic material and their properties are assumed to be varying continuously across the thickness of assumed geometry(shell panel)from the lower surface(metal-rich)to the upper(ceramic rich)surface.In this analysis,the constituent material properties are also considered to be the function of temperature(T)increment.Therefore,the effective material properties ξ of the present FGM panel are the functions of both the position as well as the temperature.In order to obtain the effective material properties of FGM,various micromechanical models such as the Voigt’s model44,the Mori–Tanaka model45,and the selfconsistent method46have been proposed.Some of the studies incorporated both the Voigt’s model and the Mori–Tanaka scheme for FGM material property evaluation.47–49It is observed from the above studies that the differences between the results obtained using the Voigt’s model and the Mori–Tanaka scheme are almost negligible and the Voigt’s model is found relatively simple than the other micromechanical models.Therefore,in the present study,the Voigt’s micromechanical model is used and expressed as

where subscript‘c’and ‘m’denote the ceramic and metal constituents,respectively.The ϑcis the ceramic volume fraction in the FGM.

The temperature-dependent material properties for any material continuum can be expressed in the polynomial form as50

where ξ0,ξ-1,ξ1,ξ2and ξ3are the temperature coef ficients in a cubic fit.

Now,the volume fractions of each constituent are evaluated through the established power-law distribution and expressed as51

wherenis the power-law index and it decides the material distribution across the thickness of the present FGM shell panel.

Finally,using Eqs.(4)and(6),the effective material properties of P-FGM can be expressed as

Now,different properties of P-FGM such as elastic modulus(E),Poisson’s ratio(υ)and coef ficient of thermal expansion(α),can be evaluated using the Eq.(7).

2.4.Thermoelastic constitutive relations

The thermoelastic constitutive relations of P-FGM shallow spherical shell panel can be conceded as

2.5.Finite element formulations

The P-FGM panel is now discretised using a 9-noded isoparametric Lagrangian element using a suitable finite element approach as discussed earlier.The relationship between the displacement vector(λ0)and the nodal displacement vector(λ0i)at the mid-plane of the P-FGM shell panel can be expressed as

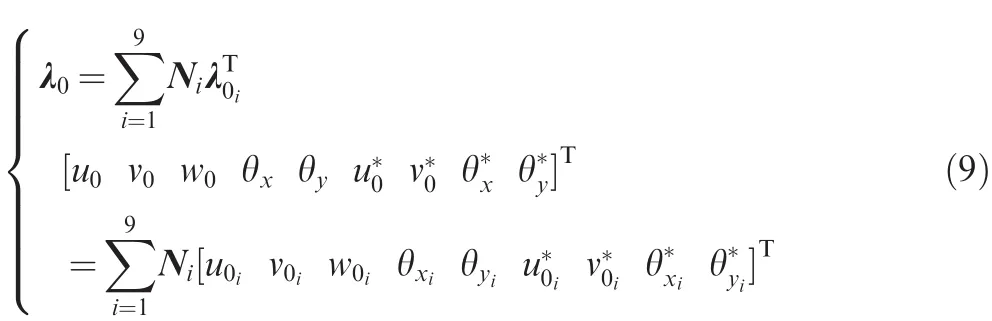
where Niis the shape functions of anyith node and the details of the shape function can be seen in Ref.52.

2.6.Governing equations

The total strain energy of the P-FGM spherical shell panel can be written as

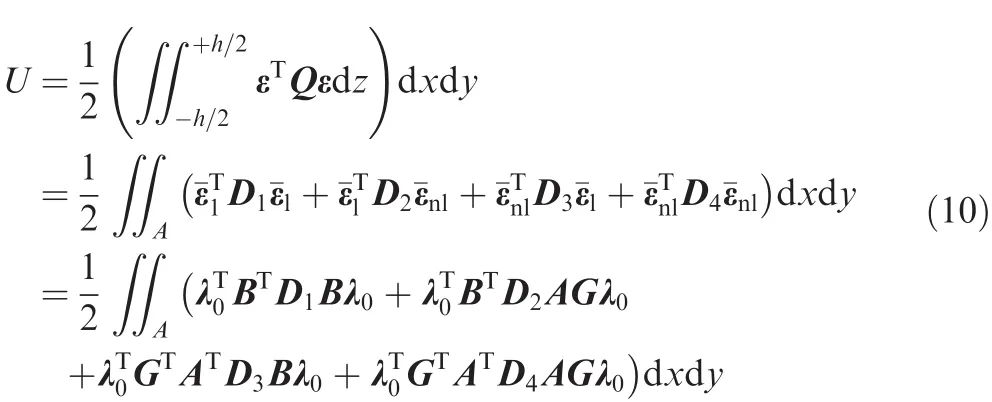
The total external work done on the P-FGM spherical shell panel due to the transverse mechanical load(q)and temperature rise(ΔT)is expressed as

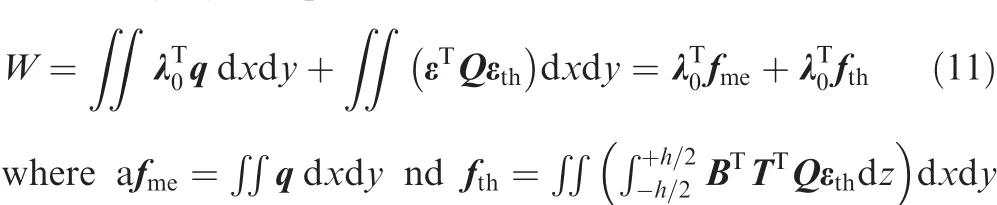
are the mechanical and thermal load vectors,respectively.

The equilibrium equation for the nonlinear bending analysis of the P-FGM spherical shell panel is obtained using the variational principle and expressed as

where Π and δ denote the total potential energy function and the variational symbol,respectively.

The final form of the equilibrium equation is derived by substituting Eqs.(10)and(11)in Eq.(12)as

where λ,Kl,Knl,Fmeand Fthare the system displacement vector,the linear stiffness matrix,the nonlinear stiffness matrix,the mechanical and thermal load vectors,respectively.Here,the system nonlinear stiffness matrix （Knl=Knl1+Knl2+Knl3）is associated with linear and nonlinear coupled stiffness matrices,say,Knl1，Knl2and Knl3，respectively.The detailed steps of evaluation of nonlinear stiffness matrix can also be seen in Ref.53.

Now the final governing equation,Eq.(13)is solved using Picard’s iterative method54through a homemade finite element computer code developed in MATLAB environment to obtain the desired nonlinear responses of the P-FGM spherical shell panel.At first step,the linear static response of the P-FGM shell panel is obtained by dropping the appropriate nonlinear terms from the final governing equation.Now,the initial static response will be used as the first input for computation of the nonlinear response with respect to the load parameters.The nonlinear responses will be updated till the two successive response values achieve the desired convergence criteria(～10-3).

3.Results and discussion

In this study,the linear and the nonlinear deformation behaviour of the P-FGM shallow spherical shell panel is examined under combined action of thermomechanical load using the temperature-dependent constituent properties.The desired responses are computed using the homemade finite element computer code developed in MATLAB environment in accordance with the developed nonlinear mathematical formulation.TheP-FGM constituentmaterialsareassumed to be temperature-dependent and the variation temperature coef ficients for the each property are presented in Table 1.If not stated otherwise,the solutions are computed using different sets of support conditions in the combination of clamped(C),simply-supported(S)and free(F)supports to avoid rigid body motion and to reduce the number of unknowns.The restricted if elds of variables at the panel edges are given as

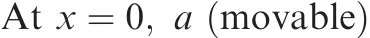
Table 1 Temperature coef ficients of FGM constituents.45

The non-dimensional forms ofthe central de flection(=w/h),the load parameter(Q=qa4/E0h4)and the axial stress(σxx=σxxa4/E0h4)parameters are presented throughout the analysis if not stated otherwise.In each formula,E0denotes the elastic modulus of the metal at ambient temperature and σxxis the axial stress value at（a/2，b/2，0）.

After the convergence and validation check,the developed nonlinear model has been extended for the additional numerical experimentations to show the effect of different parameters(the power-law indices,n,the curvature ratiosR/a,the thickness ratiosa/h,and the aspect ratiosa/b)on the linear and nonlinear deformation behaviour of the P-FGM shallow spherical shell panel.

3.1.Convergence and validation

As discussed earlier,the convergence behaviour of the proposed nonlinear finite element model is examined for a clamped P-FGM spherical shell panel(R/a=50,a/h=10)under thremomechanical load (ΔT=0, 300 K andQ=100).The linear and the nonlinear central de flection parameters are computed for different mesh sizes and presented in Fig.2.It is clearly understood from the figure that the responses converge well with mesh re finement and a 5×5 mesh is suf ficient to compute the desired responses further.

The present nonlinear model has been extended now for the comparison purpose by solving the example the same as that in Ref.29.For the computational purpose,a square FG(SUS304/Si3N4) flat panel(a/h=10)under combined thermomechanical load is analysed for three different support conditions(CFCF,CSCF,CCCC)and two power-law indices(n=0.2,2.0)(see Table 2).In particular,the support conditions are taken the same as that in Ref.29where movable and immovable in-plane support conditions are considered in thex-andydirections,respectively.The present results show good agreement with those in Ref.29for each case of the support conditions.It is also interesting to note that the differences are higher for the clamped support and higher load parameters.The difference between the results indicates the importance of the HSDT kinematics with Green-Lagrange nonlinearity including all the nonlinear higher-order terms instead of von

Fig.2 Convergence of a clamped P-FGM spherical shell panel under thermomechanical loading.

Table 2 Comparison of non-dimensional central de flection of FG flat panel.

Karman nonlinearity and HSDT kinematics as adopted in the reference.

3.2.Numerical results

Now,the present nonlinear model is extended further to compute the nonlinear responses of the P-FGM spherical shell panel for different geometrical and material parameters in this section.The responses are computed for five uniformly distributed transverse load(Q=0,50,100,150,200)parameter and two different uniform temperature rises(ΔT=0,300 K)throughout the analysis.

The effects of power-law indices on the linear()and the nonlinear()non-dimensional central de flection parameter of simply-supported square P-FGM(SUS304/Si3N4)spherical shell panel(R/a=5,a/h=10)under thermomechanical load are computed and presented in Table 3.It is observed that the bending responses increase as the power-law indices increase and the results are within the expected line.It is due to the fact that the FGM structure becomes metal-rich(n=∞)as the grading index increases and the overall stiffness of the panel reduces subsequently.It is also interesting to note that the panel exhibits higher deformations for combined thermomechanical loading case.

Table 4 presents the linear and the nonlinear nondimensional bending responses of square simply-supported P-FGM(SUS304/Si3N4)spherical shell panel(R/a=100,n=2.0)for four thickness ratios(a/h=10,20,50,100)under combined thermomechanical load.It is clearly observed from Table 4 that the linear responses decrease as the thickness ratios increase for both mechanical and/or combined load.However,the nonlinear responses follow a non-monotonous behaviour for higher mechanicalload parameter i.e.,Q=200 under the in fluence of temperature load(ΔT=300 K).

In Table 5,the deformation behaviour of simply-supported square P-FGM(SUS304/Si3N4)spherical shell panel(n=2.0,a/h=10)under thermomechanical load is examined at different curvature ratios(R/a=10,20,50,∞).The linear and the nonlinear responses increase with the curvature ratios when theP-FGMshellpanelisunderthein fluenceofmechanicalload only i.e.,ΔT=0 K.However,just a reverse trend from the thickness ratio is observed under the combined action of the mechanical and the thermal loading(ΔT=300 K).This study indicatesthatthe flatpanels areaffectedconsiderably duetothe combined action of loading instead of curved panels.

The effect of the aspect ratios(a/b=1.5,2.0,2.5)on the linear and nonlinear static responses of simply-supported P-FGM(SUS304/Si3N4)spherical shell(n=2.0,a/h=10,R/a=5)panel under combined thermomechanical load is examined and presented in Table 6.It is observed that the linear and nonlinear responses are decreasing as the aspect ratios increase.It is also interesting to note that the P-FGM spherical shell panel exhibits softening type nonlinearity under the in fluence of the thermal load.

In any deformation study,the axial stress plays an important role in design and analysis.The non-dimensional axial stress at the centre of the P-FGM shell(R/a=5,a/h=10)panel is computed from different load parameters and shownin Fig.3.It is clearly observed that the panel shows non-zero positive axial stress values under thermal load (Q=0,ΔT=300 K)only;however,the axial stress parameters decrease with the increase in power-law indices as seen in the Fig.3(a).It is also understood that the axial stress parameter is higher for the shell panel with smaller aspect ratio as shown in Fig.3(b).In addition,signi ficant differences can also be observed between the axial stress values for the panel under only mechanical load and the combined thermomechanical load as well.

Table 3 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM spherical shell panel for different power-law indices.

Table 3 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM spherical shell panel for different power-law indices.

ΔT(K) Q n=0.2 n=2.0 n=5.0wlwnlwlwnlwlwnl 0 0 0 0 0 0 0 0 50 1.4665 1.3692 1.7656 1.6184 1.8586 1.6946 100 2.9330 2.4849 3.5311 2.8876 3.7173 3.0115 150 4.3995 3.3944 5.2967 3.9054 5.5759 4.0631 200 5.8660 4.1910 7.0623 4.7457 7.4345 4.9514 300 0 -0.0060 -0.0060 -0.0038 -0.0038 -0.0070 -0.0070 50 1.6897 1.6055 2.0579 1.9181 2.1642 2.0077 100 3.3855 2.9290 4.1196 3.4313 4.3358 3.5799 150 5.0812 4.0142 6.1813 4.6368 6.5074 4.8463 200 6.7769 4.9645 8.2430 5.6843 8.6790 5.9137

Table 4 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM spherical shell panel at different thickness ratios.

Table 4 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM spherical shell panel at different thickness ratios.

ΔT(K) Q a/h=10 a/h=20 a/h=50 a/h=100wlwnlwlwnlwlwnlwlwnl 0 0 0 0 0 0 0 0 0 0 50 1.967 1.833 1.883 1.791 1.849 1.768 1.834 1.753 100 3.281 3.934 3.767 3.282 3.699 3.261 3.668 3.224 150 5.901 4.434 5.651 4.555 5.549 4.554 5.502 4.491 200 7.868 5.436 7.534 5.644 7.398 5.714 7.336 5.625 300 0 -0.010 -0.010 -0.039 -0.039 -0.192 -0.192 -0.405 -0.401 50 2.105 1.947 1.986 1.881 1.796 1.726 1.566 1.536 100 4.220 3.466 4.012 3.457 3.785 3.341 3.539 3.207 150 6.336 4.684 6.038 4.797 5.775 4.724 5.511 4.612 200 8.451 5.704 8.064 5.931 7.764 5.959 7.484 5.855

Table 5 Linear and nonlinear non-dimensional central de flection(wlandwnl)of simply-supported P-FGM spherical shell panel at different curvature ratios.

Table 6 Effect of aspect ratio on linear and nonlinear non-dimensional central de flection(wlandwnl)of simply-supported P-FGM spherical shell panel.

Fig.3 Non-dimensional axial stress of simply-supported P-FGM spherical shell panel under thermomechanical load for different power-law indices and aspect ratios.

The in fluence of various support conditions(CCCC,SSSS,SFSF and CFCF)on the non-dimensional central de flections of square P-FGM (SUS304/Si3N4)spherical shell panel(n=2.0,a/h=20,R/a=50)is analysed under combined thermomechanical load in this example and presented in Table 7.The de flection parameters show maximum and mini-mum for the SFSF and the CCCC support conditions,respectively.The spherical shell panel is showing hardening type of nonlinearbehaviourundertwo supportconditionsi.e.,clamped and simply-supported case,whereas the panel follows softening type of nonlinearity for other support conditions(SFSF and CFCF).In order to show the effect of support conditions and the combined loading effect on the deformation behaviour few deformed shapes are presented in Fig.4.For the computational purpose,the P-FGM(R/a=5,a/h=10,n=2.0)spherical shell panel is analysed under uniformly distributed transverse mechanical load parameter,Q=100 by setting the temperature increments,ΔT=0,300 K for two support conditions(CCCC and SSSS).It is clearly observed that the simply-supported shell panel shows higher deformations under combined thermomechanical load.

Tables 8 and 9 show the linear and the nonlinear responses of three different simply-supported P-FGM(SUS304/Si3N4)shell panels(Ry/Rx=0.50,0.75,1.50)for the different values of power-law indices(n=0.2,2.0,5.0)and the aspect ratios(a/b=1.5,2.0,2.5),respectively using the parameters asR/a=5 anda/h=10.The FG shell panel bending responses are computed for five mechanical loads(Q=0,50,100,150,200)by setting the thermal load,ΔT=300 K.It is clearly observed that the linear and the nonlinear responses increase with the power-law indices and decrease with the aspect ratios,irrespective of the shell con figurations.It is also noted that thede flection parameters are higher for larger values ofRy/Rxexcept few linear cases as in Table 9.

Table 7 Effect of different support conditions on linear and nonlinear non-dimensional central de flection(wlandwnl)of P-FGM spherical shell panel.

Fig.4 Deformed shape of P-FGM spherical shell panel under thermomechanical load(Q=100).

Table 8 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM shell panels for different power-law indices.

Table 8 Linear and nonlinear non-dimensional central de flection(and)of simply-supported P-FGM shell panels for different power-law indices.

Shell con figuration Q n=0.2 n=2.0 n=5.0wlwnlwlwnlwlwnl Ry/Rx=0.50 0 0.0851 0.0461 0.1136 0.1136 0.1253 0.1253 50 1.4622 0.8288 1.7974 0.9005 1.9101 0.9261 100 2.8393 1.5638 3.4812 1.7254 3.6948 1.7796 150 4.2164 2.1832 5.165 2.4236 5.4796 2.5034 200 5.5936 2.7045 6.8488 3.0004 7.2644 3.1037 Ry/Rx=0.75 0 0.0635 0.0392 0.0834 0.045 0.0927 0.0484 50 1.5642 1.0022 1.9143 1.1001 2.0284 1.136 100 3.0649 1.9296 3.7451 2.1451 3.9642 2.2152 150 4.5655 2.742 5.576 3.0591 5.8999 3.1743 200 6.0662 3.4583 7.4068 3.8558 7.8356 4.0010 Ry/Rx=1.50 0 0.0369 0.0276 0.0464 0.0318 0.0531 0.0355 50 1.6474 1.2365 2.0074 1.3903 2.1218 1.4376 100 3.2578 2.3517 3.9684 2.6564 4.1906 2.7499 150 4.8682 3.3233 5.9293 3.7523 6.2594 3.8832 200 6.4787 4.201 7.8903 4.7268 8.3282 4.8946

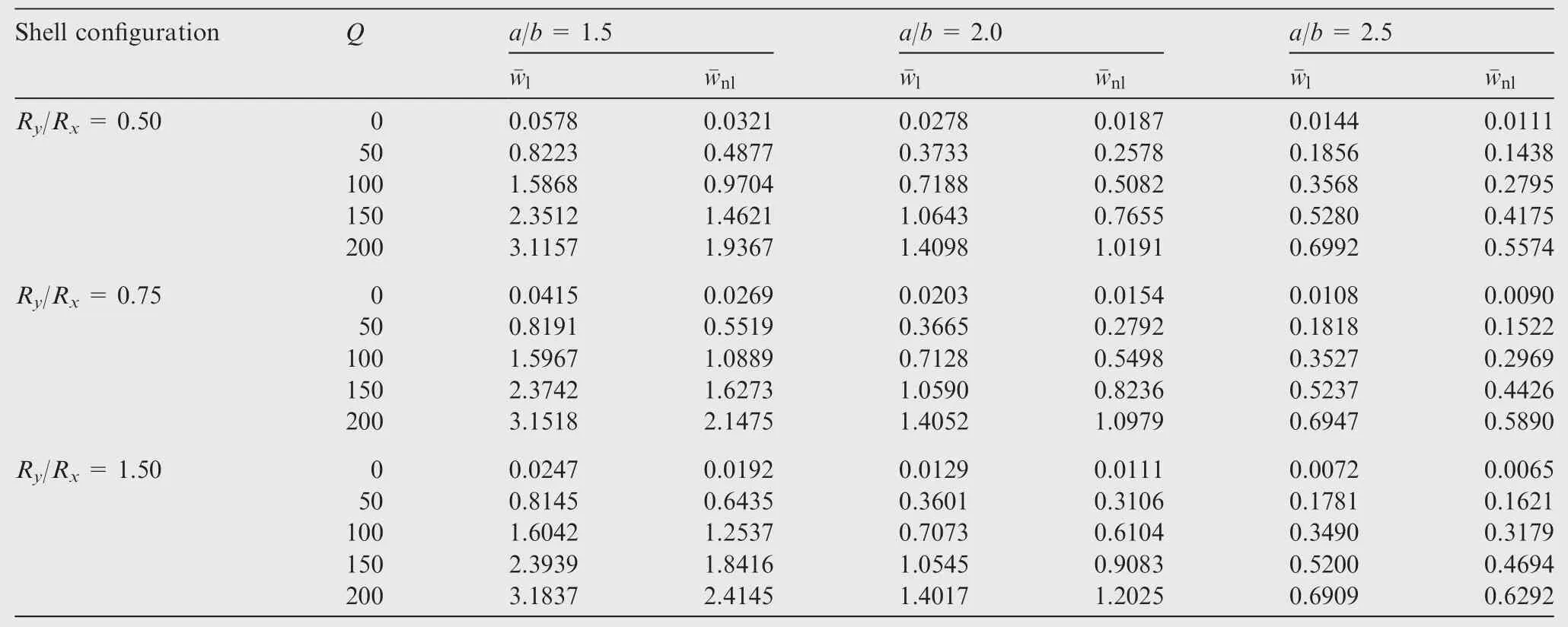
Table 9 Linear and nonlinear non-dimensional central de flection(wlandwnl)of simply-supported P-FGM shell panels at different aspect ratios.

4.Conclusions

The linear and nonlinear bending responses of the P-FGM spherical shell panel are investigated under thermomechanical load.This is the first time a general nonlinear mathematical PFGM shell panel model is developed in the framework of the HSDT and Green-Lagrange geometrical nonlinearity including all the nonlinear higher-order term to achieve the generality.Based on the comprehensive parametric study,the following concluding points are drawn.

(1)The de flection parameters are higher and lower in metalrich and ceramic-rich P-FGM shallow spherical shell panel,respectively.

(2)The de flection parameters reduce with the increase in aspect ratios and number of support constraints.

(3)The P-FGM shallow spherical shell panel exhibits maximum de flection under combined loading conditions.

(4)It is observed that as the thickness ratio increases the linear de flection parameters decrease whereas a mixed type of behaviour is found in nonlinear cases.

(5)With the increase in curvature ratio,the de flection parameters increase under mechanical load,however a reverse trend is found in case of thermomechanical load.

1.Birman V,Byrd LW.Modeling and analysis of functionally graded materialsand structures.ApplMechRev2007;60(5):195–216.

2.Yang J,Shen HS.Non-linear analysis of functionally graded plates under transverse and in-plane loads.Int J Nonlinear Mech2003;38(4):467–82.

3.Kiani Y,Akbarzadeh AH,Chen ZT,Eslami MR.Static and dynamic analysis of an FGM doubly curved panel resting on the Pasternak-type elastic foundation.ComposStruct2012;94(8):2474–84.

4.Dai KY,Liu GR,Lim KM,Han X,Du SY.A meshfree radial point interpolation method for analysis of functionally graded material(FGM)plates.Comput Mech2004;34(3):213–23.

5.Thai HT,Choi DH.A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates.Compos Struct2013;101:332–40.

6.Navazi HM,Haddadpour H.Nonlinear cylindrical bending analysis of shear deformable functionally graded plates under different loadings using analytical methods.Int J Mech Sci2008;50(12):1650–7.

7.Thai HT,Kim SE.A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates.Compos Struct2013;96:165–73.

8.Abdelaziz HH,Atmane HA,Mechab I,Boumia L,Tounsi A,Abbas ABE.Static analysis of functionally graded sandwich plates using an ef ficient and simple re fined theory.Chin J Aeronaut2011;24(4):434–48.

9.Upadhyay AK,Shukla KK.Geometrically nonlinear static and dynamic analysis of functionally graded skew plates.Commun Nonlinear Sci Numer Simul2013;18(8):2252–79.

10.Oktem AS,Mantari JL,Soares CG.Static response of functionally graded plates and doubly-curved shells based on a higher order shear deformation theory.EurJMechASolid2012;36:163–72.

11.Thai HT,Choi DH.A re fined plate theory for functionally graded plates resting on elastic foundation.Compos Sci Technol2011;71(16):1850–8.

12.Bourada M,Kaci A,Houari MSA,Tounsi A.A new simple shear and normal deformations theory for functionally graded beams.Steel Compos Struct2015;18(2):409–23.

13.Yahia SA,Atmane HA,Houari MSA,Tounsi A.Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories.Struct Eng Mech2015;53(6):1143–65.

14.Meziane MAA,Abdelaziz HH,Tounsi A.An ef ficient and simple re fined theory for buckling and free vibration of exponentially graded sandwich plates under various boundary conditions.J Sandwich Struct Mater2014;16(3):293–318.

15.Belabed Z,Houari MSA,Tounsi A,Mahmoud SR,Beg OA.An ef ficient and simple higher order shear and normal deformation theory for functionally graded material(FGM)plates.Compos Part B Eng2014;60:274–83.

16.Draiche K,Tounsi A,Khal fiY.A trigonometric four variable plate theory for free vibration of rectangular composite plates with patch mass.Steel Compos Struct2014;17(1):69–81.

17.Bousahla AA,Houari MSA,Tounsi A,Bedia EAA.A novel higher order shear and normal deformation theory based on neutral surface position for bending analysis of advanced composite plates.Int J Comput Method2014;11(6):1350082.

18.Hebali H,Tounsi A,Houari MSA,Bessaim A,Bedia EAA.New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates.J Eng Mech2014;140(2):374–83.

19.Larbi LO,Kaci A,Houari MSA,Tounsi A.An ef ficient shear deformation beam theory based on neutral surface position for bending and free vibration of functionally graded beams.Mech Based Des Struc2013;41(4):421–33.

20.Khare RK,Kant T,Garg AK.Free vibration of composite and sandwich laminates with a higher-order facet shell element.Compos Struct2004;65(3–4):405–18.

21.Pradyumna S,Bandyopadhyay JN.Static and free vibration analyses of laminated shells using a higher order theory.J Reinf Plast Compos2008;27:167–86.

22.Biglari H,Jafari AA.Static and free vibration analyses of doubly curved composite sandwich panels with soft core based on a new three-layered mixed theory.J Mech Eng Sci2010;224(11):2332–49.

23.SzekrenyesA.Stressand fractureanalysis in delaminated orthotropic composite plates using third-order shear deformation theory.Appl Math Model2014;38(15–16):3897–916.

24.Woo J,Meguid SA.Nonlinear analysis of functionally graded plates and shallow shells.Int J Solids Struct2001;38:7409–21.

25.Zhao X,Lee YY,Liew KM.Thermoelastic and vibration analysis of functionally graded cylindrical shells.Int J Mech Sci2009;51(9–10):694–707.

26.Zhao X,Liew KM.Geometrically nonlinear analysis of functionally graded shells.Int J Mech Sci2009;51(2):131–44.

27.Reddy JN.Analysis of functionally graded plates.Int J Numer Methods Eng2000;47:663–84.

28.Shen HS.Nonlinear bending response of functionally graded plates subjected to transverse loads and in thermal environments.Int J Mech Sci2002;44(3):561–84.

29.Yang J,Shen HS.Nonlinear bending analysis of shear deformable functionally graded plates subjected to thermo-mechanical loads under various boundary conditions.Compos Part B Eng2003;34(2):103–15.

30.Wattanasakulpong N,Prusty GB,Kelly DW.Free and forced vibration analysis using improved third-order shear deformation theory for functionally graded plates under high temperature loading.J Sandwich Struct Mater2013;15(5):583–606.

31.Bich DH,Tung HV.Non-linear axisymmetric response of functionally graded shallow spherical shells under uniform external pressure including temperature effects.Int J Nonlinear Mech2011;46(9):1195–204.

32.Bich DH,Dung DV,Hoa LK.Nonlinear static and dynamic buckling analysis of functionally graded shallow spherical shells including temperature effects.Compos Struct2012;94(9):2952–60.

33.Na KS,Kim JH.Nonlinear bending response of functionally graded plates under thermal loads.J Therm Stresses2006;29(3):245–61.

34.Zidi M,Tounsi A,Houari MSA,Bedia EAA,Beg OA.Bending analysis of FGM plates under hygro-thermo-mechanical loading using a four variable re fined plate theory.Aerosp Sci Technol2014;34:24–34.

35.Tounsi A,Houari MSA,Benyoucef S,Bedia EAA.A re fined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates.Aerosp Sci Technol2013;24(1):209–20.

36.Bouderba B,Houari MSA,Tounsi A.Thermomechanical bending response of FGM thick plates resting on Winkler-Pasternak elastic foundations.Steel Compos Struct2013;14(1):85–104.

37.Khal fiY,Houari MSA,Tounsi A.A re fined and simple shear deformation theory for thermal buckling of solar functionally graded plates on elastic foundation.Int J Comput Methods2014;11(5):135007.

38.Attia A,Tounsi A,Bedia EAA,Mahmoud SR.Free vibration analysis of functionally graded plates with temperature-dependent properties using various four variable re fined plate theories.Steel Compos Struct2015;18(1):187–212.

39.Hamidi A,Houari MSA,Mahmoud SR,Tounsi A.A sinusoidal plate theory with 5-unknowns and stretching effect for thermomechanical bending of functionally graded sandwich plates.Steel Compos Struct2015;18(1):235–53.

40.Houari MSA,Tounsi A,Beg OA.Thermoelastic bending analysis of functionally graded sandwich plates using a new higher order shearand normaldeformation theory.IntJMechSci2013;76:102–11.

41.Pandya BN,Kant T.Finite element analysis of laminated composite plates using a higher-order displacement model.Compos Sci Technol1988;32(2):137–55.

42.Reddy JN.Mechanics of laminated composite:Plates and shells–theory and analysis.Boca Raton,FL:CRC Press;2004.p.456–7.

43.Kar VR,Panda SK.Nonlinear free vibration of functionally graded doubly curved shear deformable panels using finite element method.JVibControl2014. http://dx.doi.org/10.1177/1077546314545102.

44.Gibson LJ,Ashby MF,Karam GN,Wegst U,Shercliff HR.The mechanical properties of natural materials.II.Microstructures for mechanical ef ficiency.Proc R Soc A1995;450(1938):141–62.

45.Mori T,Tanaka K.Average stress in matrix and average elastic energy of materials with mis fitting inclusions.Acta Metall1973;2(5):571–4.

46.Hill R.A self-consistent mechanics of composite materials.J Mech Phys Solids1965;13(4):213–22.

47.Shen HS,Wang H.Nonlinear vibration of shear deformable FGM cylindrical panels resting on elastic foundations in thermal environments.Compos Part B Eng2014;60:167–77.

48.Shen HS,Wang ZX.Assessment of Voigt and Mori–Tanaka models for vibration analysis of functionally graded plates.Compos Struct2012;94(7):2197–208.

49.Shen HS.Thermal postbuckling of shear deformable FGM cylindrical shells surrounded by an elastic medium.J Eng Mech2013;139(8):979–91.

50.Reddy JN,Chin CD.Thermoelastical analysis of functionally graded cylinders and plates.JThermStresses1998;21(6):593–626.

51.Shen HS.Functionally graded material:nonlinear analysis of plates&shells.Boca Raton,FL:CRC Press;2009.p.22–3.

52.Cook RD,Malkus DS,Plesha ME,Witt RJ.Concepts and applications of finite element analysis.Singapore:John Wiley&Sons;2009.p.215–6.

53.Kar VR,Panda SK.Large deformation bending analysis of functionally graded spherical shell using FEM.Struct Eng Mech2015;53(4):661–79.

54.Reddy JN.An introduction to nonlinear finite element analysis.Cambridge,UK:Oxford University Press;2004.p.443–4.