巧用错误,构建多姿多彩的数学课堂
何丽梅
[摘 要]课堂是教学的主阵地.课堂离不开师生互动,生生互动.在互动的过程中,学生难免会出现一些错误.教师若能利用好“错误”这一宝贵资源,引导学生完成新知探究,必将能构建多姿多彩的课堂,让数学变得鲜活,让学生爱上数学.
[关键词]数学课堂 巧用 错误
[中图分类号] G633.6 [文献标识码] A [文章编号] 16746058(2016)110016
古人云:人非圣贤,孰能无过.在课堂教学中,学生对知识的理解会出现各种各样的偏差,有的教师在学生出现错误时,也许会“马上制止”或“立即纠正”.但这样做却不能达到预期效果,“一错再错”的现象仍然不时发生.认知心理学派认为,错误是学习的必然产物,学生的知识背景、思维方式、情感体验、表达形式各有不同,他们在学习的过程中出现错误是十分正常的.课堂是学生出错的地方,出错是学生的权利.心理学家盖耶认为:谁不考虑尝试错误,不允许学生犯错误,就将错过最富成效的学习时刻.
作为教师,我们要善待学生的“错误”,要抓住这种宝贵的数学教育契机,让“错误”变成良好的教学资源.多年的课堂教学实践使我认识到,如果能在课前精心预设“错误”资源,课堂中敏锐地捕捉“错误”,那么,学生是可以少犯甚至不犯错误的,而我们的数学课堂也会因此而变得更加生动多姿,高效出彩.
一、课前精心预设“错误”,让概念课变得鲜活起来
“问渠哪得清如许,为有源头活水来”.刘绍学先生曾说过,数学是清楚的,清楚的前提,清楚的推理,得出清楚的结论.概念课教学是高中数学教学的重头戏,新概念的理解在数学学习中也非常关键.学生对新概念的理解常常会遇到一些常见的、易犯的错误,尽管教师反复讲解,多次强调,总有些学生会一知半解,对于这种情况,教师可通过认真钻研教材,根据学生的认知规律和凭借教学经验预测学生学习某知识时可能发生的错误.在课堂教学中运用预设的“错误”资源,让学生在思索、讨论中展现鲜活的课堂.
【课例1】“零点存在性定理”的学习,如果直接将结论抛给学生,让学生生硬地记下来,解题应该是没问题的,可是学生会有疑惑:为什么要有这些条件呢?为了让学生知其然,也知其所以然,我预设了以下问题让学生思考辨析.请以函数图像为例,说明以下问题,若成立,请说明理由;若不成立,请举出反例.
(1)若函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则函数y=f(x)在区间(a,b)内一定有零点吗?
(2)若函数y=f(x)在区间[a,b]上是连续不断的曲线,
且f(a)f(b)>0,则函数y=f(x)在区间(a,b)内一定有零点吗?
(3)若函数y=f(x)在区间[a,b]上是连续不断的曲线,且f(a)f(b)<0,你能确定函数y=f(x)在区间(a,b)内的零点个数吗?
学生通过分组讨论和动手画图,得出如下结果:(1)若函数y=f(x)不是连续函数,结论不成立;(2)函数不一定存在零点;(3)函数零点个数不确定,但至少有一个零点.最后通过以上三个问题的探究,学生总结了零点存在须具备的两个条件:①函数是连续函数;②在区间端点处函数值异号.这个结论是通过“试误”得出的.学生在探究的过程中,不仅明确了“有什么”,更明白地知道“为什么”.分组探讨能使课堂气氛热烈,新知的获得会让学生觉得倍有成就感,为后续的学习创设了良好的情绪体验.
【课例2】“空间几何体的结构”教学中,“棱台”的概念辨析可以通过教材第9页第2题三个几何体的比较和认识进行.学生通过辨析会认识到,棱台的本质是与棱锥相关的,即可以理解为各侧棱延长后相较于同一点的几何体.这样教学,对棱台的认识不仅准确,而且深刻,不会随时间推移而淡忘.
【课例3】“直线与平面平行的判定定理”的教学中,学生在观察实例演示后,有以下的一些叙述:(1)如果直线aα,且a∥b,则a∥α;(2)如果a∥b,且bα,则a∥α;(3)如果a∥b,则a∥α.这三个命题的提出,引得学生踊跃发表自己的看法.这时我抓紧机会引导学生对以上三个命题进行辨析,学生归纳得出:判定线面平行须具备三个条件,缺一不可,可以将定理简记为“线线平行则线面平行”.正是对“错误”的充分认识,学生对“正确”的理解也就更深刻.
通过精心的课前预设“错误”,数学概念不再是硬生生的冷道理,概念课也不再枯燥无味,而是变得生动活泼,富有生命力和感染力,学生认识到,数学是讲道理的,数学新知识的探究过程是有趣的.
二、例题评析及时捕捉“错误”,让数学思维过程充分暴露
《数学课程标准》指出:“要关注学生在数学活动中所表现出来的情感与态度,帮助学生认识自我,建立信心.”良好的数学情感与态度是学生参与数学活动的重要动力,是克服困难和探索创新的力量源泉.课堂上,学生思维过程暴露的错误,教师若能及时关注,善于捕捉,“错误”也会变为一种教学资源.只要合理利用,能较好地促进学生情感的发展.对激发学生的学习兴趣,唤起学生的求知欲具有特殊的作用.
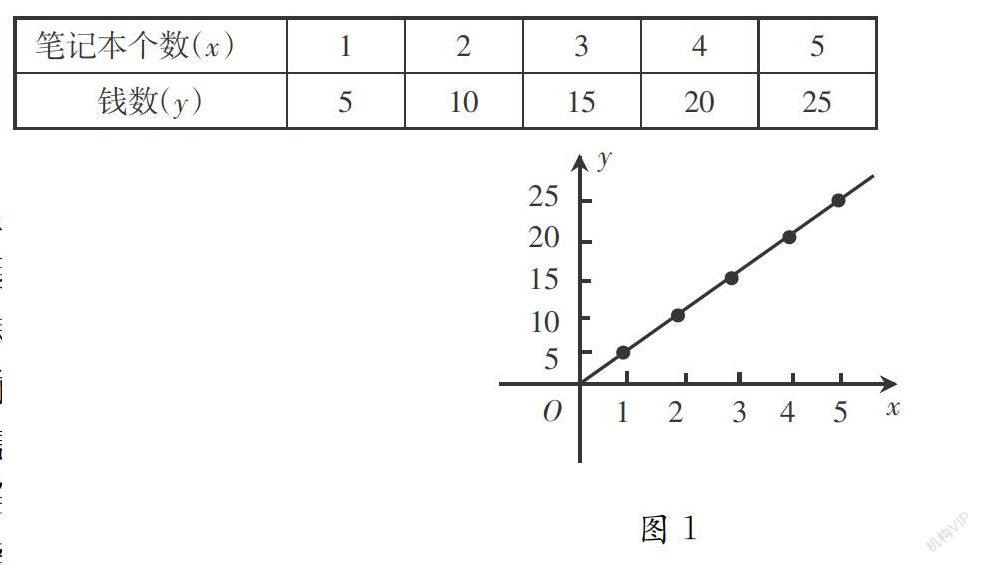
【课例4】“函数的表示法”教学中,有这样一个例题:某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x).
学生小李很快就完成了这道题,并举手示意要展
示他的作业,于是我让他到黑板前板演.他是这样写的:用解析法,函数y=f(x)表示为y=5x;用列表法,函数y=f(x)表示为下表
用图像法,函数y=f(x)可表示为如图1.小李写完后,看着我,期待得到表扬和肯定.我微笑着说,你写得真快,字迹工整又漂亮,很好.下面请同学们来给小李评一评,看看他的答案可以得满分不?于是学生开始评议.声音渐渐平息的时候,有学生站起来说:“老师,我认为他的答案是不完整的,不能得满分.”我装作很诧异的样子问:“为什么呢?”学生接着说,他在用图像法表示函数时出错了,函数图像不是线段,而应该是五个点.大多数学生表示赞同,也有少数学生表示疑惑.这时学生继续说道,因为函数的自变量x只能取五个值啊,分别是1,2,3,4,5,所以对应的函数值就只有相应的五个值,图像就是五个点啊.刚才还面带疑惑的学生听了他的解释后恍然大悟.此时我抓住时机继续追问,这道题用图像法表示,应该是五个点,那么,其他两种表示方法有没有错误的地方呢?为什么会出现这种错误呢?学生很快指出,第一种解析法中,少写了定义域,应补上.出现这种错误的原因,就是忽略了函数的三要素之一:定义域.
这个例题的解析,让学生充分暴露了他们的思维过程,在这个过程中学生“发现错误”并“纠正错误”,比教师一遍遍强调注意事项,效果要好得多,学生对知识的理解和掌握也更牢固.在数学教学过程中,教师如果从学生出现错误时进行引导点拨,不仅能引出正确的想法,还可以“将错就错”,拓宽学生的思维.同时也使教学环节更加精彩,教学过程更加真实.
《数学课程标准》指出:“人人学有价值的数学;人人都能获得必需的数学;不同的人在数学上获得不同的发展.”数学教学应最大限度地满足每一个学生的需要,最大限度地开启每一个学生的智慧潜能.真实的课堂教学,不可能不出现错误,正是因为有了这样那样的错误,课堂才会绚丽多姿.教师若能利用好这些“错误”,化弊为利,不仅能使不同层次的学生发现错误,提高学习的积极性,而且可以扬长补短,拓宽学生的思维,训练学生思维的灵活性和创造性.这样的课堂也必定是最真实的,最有活力,最有创造力的.
(责任编辑 黄桂坚)

