半平面中解析函数的复合边值逆问题

武模忙

（商丘学院，河南　商丘　476000）

半平面中解析函数的复合边值逆问题

武模忙

（商丘学院，河南商丘476000）

给出半平面中解析函数的复合边值逆问题的提法，并给出了其解法，即利用消元法，将其转化为半平面中的复合边值问题进行求解，得到半平面中复合边值逆问题的解中的未知解析函数.把所求得的解析函数代入此边值逆问题的边值条件，利用实轴上的Plemelj公式等复变函数论中的运算方法和技巧，求出此边值逆问题的解中的未知边界函数.从而，得到了该边值逆问题的全部解的具体积分表达式及可解条件.

复合边值逆问题；Riemann边值问题；Hilbert边值问题；复合边值问题

复分析中解析函数的边值问题在物理学和工程技术等许多实际问题中有着广泛而重要的应用，其已有丰富和成熟的研究成果.对于解析函数边值逆问题的研究，也逐渐成为研究的热点.文献[1-2]从力学背景出发，初步探讨了特殊情形下的解析函数Riemann边值逆问题.文献[3]讨论了由路见可教授提出的在一般情形下一类解析函数Riemann边值逆问题.文献[4]在文献[3]的启发下，提出了更一般的解析函数Riemann边值逆问题.文献[5-6]分别研究了解析函数在单位圆和半平面中的Hilbert边值逆问题，讨论了问题的可解性，并给出了问题的可解条件和解的积分表达式.

解析函数的复合边值问题在实际问题中有重要的应用价值.文献[7]对实轴上的复合周期边值问题进行了研究，文献[8]则讨论了在由光滑封闭曲线围成的区域上解析函数的复合边值逆问题的可解性.本文在此基础上进一步讨论了半平面中解析函数的复合边值逆问题，依据半平面中的解析函数Hilbert边值问题的相关结论，得到了此边值逆问题的可解条件和解的积分表达式，并给出了该边值逆问题的可解性定理.

1　问题的提出

设Z+为上半平面，Z-为下半平面；L=X为实轴.记L0=是Z+内有限条互相外离的封闭光滑曲线组，规定各Lj的正向为顺时针方向.Dj-为Lj所围的内域.D0+为X与L0之间的区域.

本文将讨论下一有关解析函数的边值逆问题，称为解析函数在半平面中的复合边值逆问题，简称为RH0-1问题.

求一组函数(Φ(z)，Ψ1(t),Ψ2(x)),其中Φ(z)在Z+内分区全纯，以L0为跳跃曲线，且在上连续；Ψ1(t)为L0上的系数函数，且Ψ1(t)∈H(L0)；Ψ2(x)为X上的实系数函数，且Ψ2满足以下边值条件：

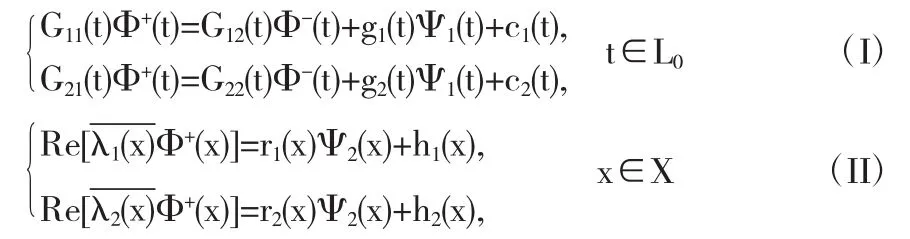
其中

Gpq(t),gp(t),cp(t)(p=1,2；q=1,2)都是L0上的已知函数，且均在L0上属于H类；λp(x)=ap(x)+ibp(x)(p=1,2)为X上的已知复函数，且在X上属于类，ap(x)，bp(x)，rp(x)，hp(x)(p=1,2)都是在X上属于类的已知实函数，且r1(x)≠r2(x).

记

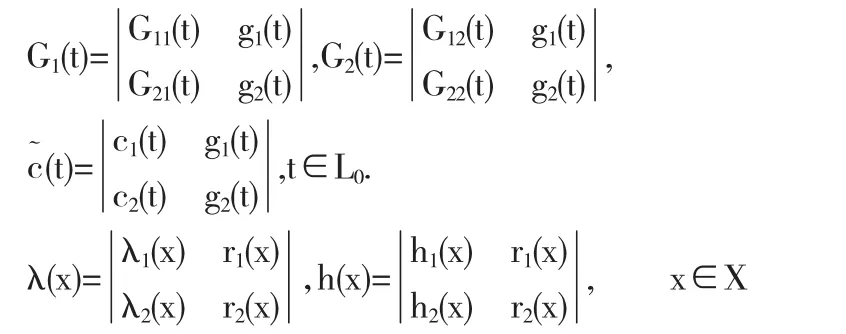
若G1(t)≠0，G2(t)≠0且λ1(x)≠0，则称上述逆问题为正则型RH0-1问题，否则称为非正则型RH0-1问题.本文仅讨论正则型RH0-1问题.

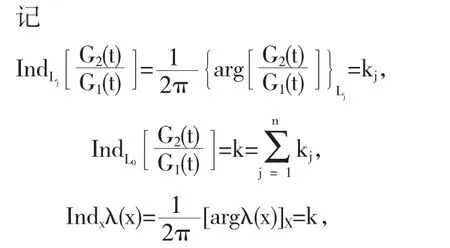
而记K=k+k.2K称为所提RH0-1问题的指标.

2　问题的转化

对于边值条件（I），第一式两端乘g2(t)减去第二式两端乘g1(t)，可得，

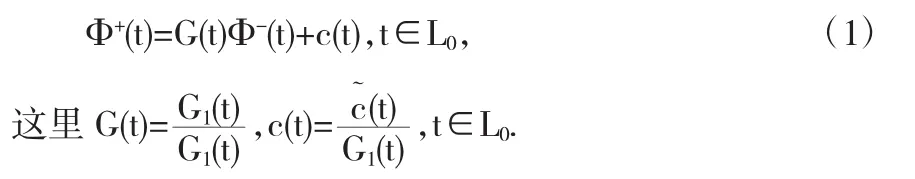
对于边值条件（II），第一式两端乘r2(x)减去第二式两端乘r1(x)，可得，

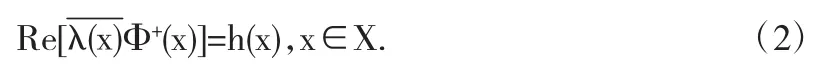
那么，若求同时满足RH0-1问题边值条件（I）、（II）的分区全纯函数Φ(z)，即求由方程（1）、（2）构成的半平面中解析函数复合边值问题：

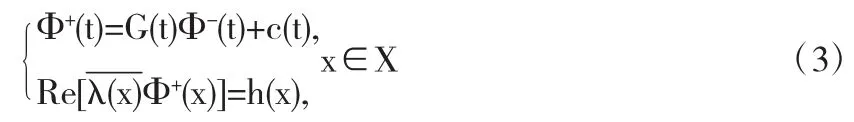
由文献[9]，可求出方程（1）的一般解为：

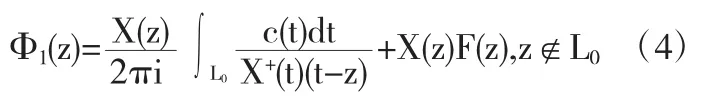
这里，

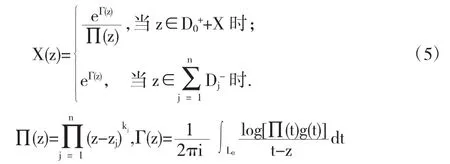
其中，zj为Dj-中任意取定的一点.F(z)是在Z+内全纯，在上连续的任意函数，以下不妨取F(z)=0.

反之，若Φ0(z)在z+内全纯，在上连续，则由（7）式确定的分区全纯函数Φ(z)必然满足方程（1）.

这样，提出的RH0-1问题就转化求在Z+内全纯，在上连续的全纯函数Φ0(z)，使它满足由（2）转化的相应条件.把（7）式代入（2）式中，可得

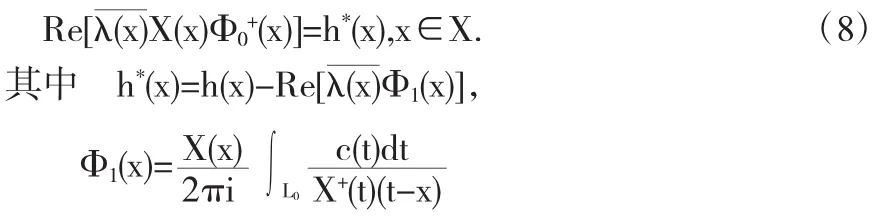
引理设X为实轴，L为CX内一封闭光滑曲线，z为L所围区域内一点.若

3　问题的求解

3.1半平面中Hilbert边值问题（8）的解

由文献[9]可得，（i）当k≥0时，问题（8）的一般解为：

3.2问题的求解

3.2.1Φ(z)的表达式

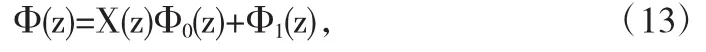
其中，（i）当K≥0时，Φ0(z)为（9）式.

（ii）当K＜0时，当且仅当（11）式成立时，Φ0(z)为（12）式.此时，Φ(z)为唯一解.

Φ1(z)、X(z)分别为（4）式和（5）式.

3.2.2Ψ1(t)的求解

将Φ(z)代入（I）中，第一式两端乘G22(t)减去第二式两端乘G12(t)，可得：

其中，（i）当K≥0时，Φ0(t)为将（9）式中的z换成t即得；当K＜0时，当且仅当（11）式成立时，Φ0(t)为将（12）式中的z换成t即得.

（ii）对（4）式、（5）式利用Plemelj公式，可得，

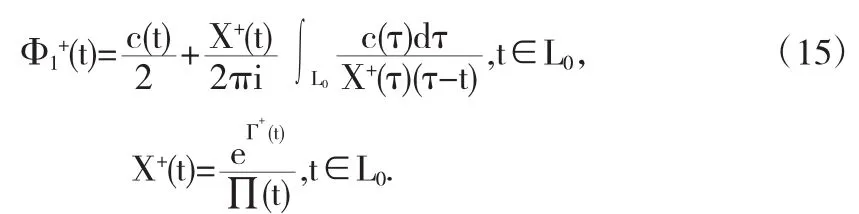
（iii）

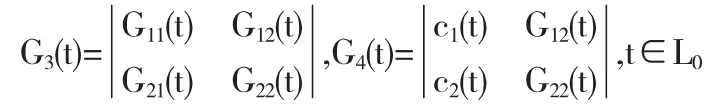
3.2.3Ψ2(t)的求解

定理对于正则型RH0-1问题，其一般解为(Φ(z),Ψ1(t),Ψ2(x)).当K≥0时，Φ(z),Ψ1(t),Ψ2(x)分别为（13），（14），（27）式；当K＜0时，当且仅当（11）式成立时，Φ(z),Ψ1(t),Ψ2(x)分别为（13），（14），（33）式，且其为唯一解.

〔1〕N.I.Ioakimids，E.A.Perdiosand K.E.Papadakis，Numerical estimation of the coefficient of the homogeneous Riemann—Hilbert problem on the basis of boundary data，Applied Mathematics and Computation，41(1991)，No.1.

〔2〕Li Xing（李星），The inverse Riemann boundary value jump problem，Proceeding of the International Conference on Computation Engineering Science.Technology Publications，Atlanta，Ga，USA，1992.

〔3〕李星.一类Riemann边值逆问题[J].数学杂志，1996,16（3）：303-306.

〔4〕王明华.Riemann边值逆问题与奇异积分方程组[J].数学杂志，1999,19（2）：175-180.

〔5〕王明华.一类Riemann－Hilbert边值逆问题[J].纯粹数学与应用数学，2006,28（2）：225-231.

〔6〕王明华.半平面中的Hilbert边值逆问题[J].四川师范大学学报:自然科学版，2011,34（2）：208-212.

〔7〕朱军明.一类复合周期性边值问题的解法[D].武汉大学，2004.

〔8〕武模忙，林峰，李锦成.解析函数的复合边值逆问题[J].华侨大学学报：自然科学版，2014,35（4）：476-480.

〔9〕路见可.解析函数边值问题教程[M].武汉：武汉大学出版社，2009.12.

O175.8

A

1673-260X（2016）09-0001-03

2016-05-14