Subsurface 1-distance of the Handlebody

SUN DONG-QI

（College of Science，Harbin Engineering University，Harbin，150001）

Subsurface 1-distance of the Handlebody

SUN DONG-QI

（College of Science，Harbin Engineering University，Harbin，150001）

For a handlebody H with∂H=S，let F⊂S be an essential connected subsurface of S.Let C（S）be the curve complex of S，AC（F）be the arc and curve complex of F，D（H）⊂C（S）be the disk complex of H and πF（D（H））⊂AC（F）be the image of D（H）in AC（F）.We introduce the definition of subsurface 1-distance between the 1-simplices of AC（F）and show that under some hypothesis，πF（D（H））comes within subsurface 1-distance at most 4 of every 1-simplex of AC（F）.

handlebody，curve complex，arc and curve complex，subsurface 1-distance

2010 MR subject classification:57M99

Document code:A

Article ID:1674-5647（2O16）O4-O375-O8

1　Introduction

In 1981，Harvey［1］introduced the curve complex C（S）of a surface S which is a finitedimensional simplicial complex，and it was intended to capture some properties of combinatorial topology of S.Hempel［2］applied it to study the distance of Heegaard splittings of 3-manifolds.See［3］for a survey that gives a good account of the history of the mathematics of the curve complex，continuing up to the recent advance.

Arc and curve complex of a surface F is another complex of F which can be known as the generalization of curve complex of F.Johnson［4］applied it to show that if the subsurface distance of a Heegaard splitting is large，then any other Heegaard surface also contains this subsurface.Li［5］proved that under some conditions，if the 3-manifold M is not a I-bundle of surface S，then the image of disk complex has diameter at most 6 in AC（S）.

Distance of the Heegaard splittings of a 3-manifold is the distance between O-simplex of curve complex C（S）.We introduced the concept of a 2-path between two 1-simplices in C（S）and proved that C（S）is P1-connected（see［6］）.Using the 2-path，we defined the 1-distance between two 1-simplices in C（S）.

In this article，we introduce the subsurface 1-distance between 1-simplices of AC（F）and discuss the upper bound of subsurface 1-distance under some hypothesis.In Section 2，we give some basic definitions.In Section 3，we introduce the subsurface 1-distance between 1-simplices of AC（F）and prove the main theorem.

2　Preliminaries

In this section we review some basic definitions.The definitions and terminologies not mentioned here are standard，see［7］.

A simplicial complex consists of a family of vertices and a family of simplices.Simplices are non-empty finite sets of vertices，subject only to the following two conditions:a nonempty subset of a simplex σ is a simplex（which is called a face of σ）；every vertex belongs to some simplex.Let σ=｛v0，v1，...，vp｝be a simplex.p is called the dimension of σ，and is denoted by dimσ，i.e.，dimσ=the number of the vertices in it minus 1.A 1-dimensional simplex is also called an edge.For a simplex σ，we denote the set of vertices of σ by vet（σ）. Definition 2.1Let S=Sg，bbe a genus g surface with b boundary components.The curve complex C（S）is defined as follows:The vertices of C（S）are the isotopy classes of non-trivial circles on S.A simplex of C（S）is a set of vertices｛γ0，γ1，...，γp｝such that γ0=〈C0〉，γ1=〈C1〉，...，γp=〈Cp〉for a collection of pairwise disjoint and non-parallel circles C0，C1，...，Cp.

Clearly，C（Sg，b）=∅if g=O and b=O，1，2 or 3；dimS1，0=O；for the other cases of g and b，dimC（Sg，b）=3g-4+b.

Definition 2.2Let H be a handlebody with∂H=S.Let D（H）be the subcomplex of C（S）with each vertex of D（H）corresponding to a curve that bounds a compressing disk in H.The D（H）is called the disk complex of H.

Definition 2.3Let S=Sg，bbe a genus g surface with b boundary components.The arc and curve complex AC（S）is defined as follows:The vertices of AC（S）are the isotopy classes of essential（non-peripheral）simple closed curves and properly embedded arcs on S. A simplex of AC（S）is a set of vertices｛γ0，γ1，...，γp｝such that γ0=〈C0〉，γ1=〈C1〉，...，γp=〈Cp〉for a collection of pairwise disjoint and non-parallel essential circles or arcs C0，C1，...，Cp.

If S is an annulus，then there are no essential closed curves，and the isotopy classes of essential arcs should have taken rel endpoints.

In this article，we do not distinguish between the vertex of C（S）（AC（S））and its representation element.

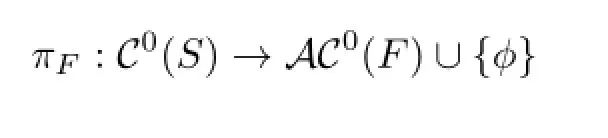
If F is a connected proper essential subsurface in S which is not an annulus，then there is a mapdefined as follows（see［8］）:Given a simple closed curve γ in S，isotope it to intersect∂F minimally.If the intersection is empty，then let πF（γ）=ϕ.Otherwise consider the isotopy classes of components of F∩γ as vertices in AC（F），and select（arbitrarily）one vertex to be πF（γ）.

Let H be a handlebody with∂H=S and F⊂S be a connected proper essential subsurface of S.Let πF（D（H））be the collection of πF（γ），where γ is any essential simple closed curve in S which is the boundary of an essential disk in H.

Definition 2.4Let S=Sg，b，and α，γ be two vertices in C（S）（AC（S））.An edge-path in C（S）（AC（S））from α to γ is a finite sequence β0，β1，...，βnof vertices in C（S）（AC（S））such that β0=α，γ=βn，and the adjacent βj-1，βjare vertices of an edge in C（S）（AC（S））for 1≤j≤n.n is called the length of the edge-path.C（S）（AC（S））is connected if for any two vertices α，γ in C（S）（AC（S）），there is an edge path from α to γ.

In［6］，we introduced the following definitions.

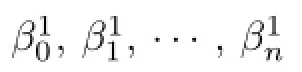
Definition 2.6Let S=Sg，b.For any two 1-simplices α1，γ1in C（S），the 1-distance of α1and γ1is defined to be the minimal length of all 2-paths in C（S）from α1to γ1，and is denoted by d1（α1，γ1）.

3　Subsurface 1-distance

Similar to the Definitions 2.5 and 2.6，we can define the 2-path in AC（F）and subsurface 1-distance between 1-simplices of AC（F）.

Definition 3.2Let S=Sg，0and F⊂S be a connected essential subsurface of S.For any two 1-simplices α1，γ1in AC（F），the subsurface 1-distance of α1and γ1is defined to be the minimal length of all 2-paths in AC（F）from α1to γ1，and is denoted by d1（α1，γ1）.

Now we give the main theorem.

Theorem 3.1Let S be the boundary of a handlebody H of genus g≥3.Let F⊂S be an essential connected subsurface of S with X（F）≤-2.If SF is compressible in H with the sum of genera of every compressible component of SF at least 2，then πF（D（H））comes within subsurface 1-distance at most 4 of every 1-simplex of AC（F）.Proof.We claim that SF must contain a 1-simplex｛δ1，δ2｝∈D（H）such that F can be connected by path to either side of δi（i=1，2）:Compressibility of SF and the genus of SF yields some meridians，which have the desired property if they are nonseparating in S. If they are separating，then we can find the nonseparating meridians in SF.

Since each of β1and β2is an essential simple closed curve or embedded arc in F，we need to consider three possibilities，namely，both of β1and β2are essential simple closed curves，one of β1and β2，say β1，is an essential simple closed curve and β2is an essential embedded arc，and both β1and β2are essential embedded arcs.

Suppose that both β1and β2are essential simple closed curves in F.There are three cases to discuss.

Case 1.Both β1and β2are separating in F.

Now the surface Fβ1，β2=F（β1∪β2）has three components，denoted by X1，X2and X3.Without loss of generality，suppose that X2contains the cutting sections of both β1and β2，X1contains a cutting section of β1and X3contains a cutting section of β2.

If the four arcs γ1，γ2，γ3，γ4are pairwise non-isotopic，then there are several possibilities for them.If γ1，γ2⊂∂X1，γ3⊂∂X2and γ4⊂∂X3，then we can choose α1in X1such that α1∩β1=α1∩β2=ϕ.Now there exists an essential arc or curve α in X3which is disjoint from α1，β2and α2，so the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2⊂∂X2，γ3⊂∂X1and γ4⊂∂X3，then we can choose α1in X2such that α1∩β1=α1∩β2=ϕ.Since β2is essential in F，there exists an essential curve or arc α in X3which is disjoint from α1，β2and α2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ3⊂∂X1，γ2⊂∂X2and γ4⊂∂X3，then we can choose α1such that it is disjoint from β2.At this time，there exists an essential arc α in X1connecting γ1and γ3which is disjoint from α1，α2，β1and β2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ3⊂∂X2，γ2⊂∂X1and γ4⊂∂X3，then we can choose α1such that it is disjoint from β2.At this time，there exists an essential arc α in X2，which is connecting γ1and γ3and is disjoint from α1，α2，β1and β2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2⊂∂X1and γ3，γ4⊂∂X2，then we can choose α1in X1and α2in X2such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ3⊂∂X1and γ2，γ4⊂∂X2，then we can chooseα1and α2such that αi∩β2=ϕ（i=1，2）.At this time，we can choose an essential arc or curve α in X3such that α∩αi=α∩βi=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ3⊂∂X1and γ2，γ4⊂∂X3，then we can choose α1and α2such that X2（α1∪α2）has a non-disk component.So there exists an essential curve α in X2which is disjoint from αi（i=1，2）and βi（i=1，2）.There exists an essential arc α′in X3connecting γ2and γ4such that α′∩α1=α′∩α2=α′∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 4.If γ1，γ2，γ3⊂∂X1and γ4⊂∂X2，then we can choose α1in X1such that α1∩βi=ϕ（i=1，2）.Now there exists an essential arc α in X1，which is connecting γ1and γ3and is disjoint from α1，α2，β1and β2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is at most 3.If γ1，γ2，γ3，γ4⊂∂X1，then we can choose α1and α2such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2and γ1，γ3，γ4are pairwise non-isotopic，then we can choose α1in X1such that α1∩β1=α1∩β2=ϕ.Similar to the former discussion，there exists an essential curve or arc α with α∩αi=α∩βi=ϕ（i=1，2），no matter which components of F（β1∪β2）the γ3and γ4belong to.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is at most 3.

If γ1=γ3and γ1，γ2，γ4are pairwise non-isotopic，then there exists an essential arc α in X1such that∂α∈γ1and α∩αi=α∩βi=ϕ（i=1，2）.If αi∩βj/=ϕ（i，j=1，2），then there exists an essential curve or arc α′in X3such that α′∩β2=α′∩α2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 4.If one of α1and α2，say α1，is disjoint from one curve of β1and β2，say β2，then the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.

If γ1=γ2，γ3=γ4and γ1，γ3are non-isotopic，then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ3，γ2=γ4and γ1，γ2are non-isotopic，then γ1and γ2have two possibilities.If γ1⊂∂X1and γ2⊂∂X2，then we can choose αi（i=1，2）such that αi∩β2=ϕ（i=1，2）. Since X3is not an annulus，there exists an essential curve or arc α in X3which is disjoint from β2，α1and α2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1⊂∂X1and γ2⊂∂X3，then there exists an essential arc or curve α in X2such that α∩αi=α∩βi=ϕ（i=1，2）.Since X3is not an annulus，there exists an essential arc or curve α′in X3which is disjoint from β2and αi（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 4.

If γ1=γ2=γ3and γ1，γ4are non-isotopic，then we can choose α1such that α1∩βi=ϕ（i=1，2）.If γ1and γ4are belong to the same component of F（β1∪β2），then we can choose α2such that α2∩βi=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1and γ4are belong to different component of F（β1∪β2），say X1and X3，then there exists an essential arc or curve α in X2which is disjoint from αi（i=1，2）and one of β1and β2.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.

If γ1=γ2=γ3=γ4，then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）. So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

Case 2.One of β1and β2，say β1，is separating in F，and β2is nonseparating in F.

Now the surface Fβ1=Fβ1has two components，denoted by X1and X2.Suppose β2⊂X2.

If the four arcs γ1，γ2，γ3，γ4are pairwise non-isotopic，then there are several possibilities for them.If γi⊂X1（i=1，2，3，4），then we can choose αi（i=1，2）in X1such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γi⊂X2（i=1，2，3，4），then we can choose αi（i=1，2）in X2such that αi∩β1=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose αi（i=1，2）in X2such that αi∩β2=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ2⊂X1and γ3，γ4⊂X2，then we can choose α1in X1such that α1∩βi=ϕ（i=1，2）. Since β2is nonseparating，we can choose α2in X2such that α2∩βi=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ3⊂X1and γ2，γ4⊂X2，then there exists an essential arc α in X1connecting γ1and γ3such that α∩αi=α∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose αi（i=1，2）such that αi∩β2=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2，γ3⊂X1and γ4⊂X2，then we can choose α1in X1such that α1∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ2，γ3⊂X2and γ4⊂X1，then there exists an essential arc α in X1such that α∩α2=α∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose α1such that α1∩βi=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.

If γ1=γ2and γ1，γ3，γ4are pairwise non-isotopic，then there are several possibilities for them.If γ1⊂X1and γ3，γ4⊂X2，then we can choose α1in X1and α2in X2such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ3⊂X1and γ4⊂X2，then we can choose α1such that α1∩βi=ϕ（i=1，2）. Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ3⊂X2and γ4⊂X1，then we can choose α1in X2such that α1∩β1=ϕ.There exists an essential curve or arc α in X1with α∩αi=α∩βi=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.

If γ1=γ3and γ1，γ2，γ4are pairwise non-isotopic，then there are several possibilities for them.If γ1⊂X1and γ2，γ4⊂X2，then there exists an essential arc or curve α in X1with α∩αi=α∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose αi（i=1，2）such that αi∩β2=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2⊂X1and γ4⊂X2，then we can choose α1in X1with α1∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γi⊂X1（i=1，2，4），then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2=γ3and γ1，γ4are pairwise non-isotopic，then similar to the former discussion，we can see that the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2=γ3=γ4，then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）. So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

Case 3.Both β1and β2are nonseparating in F.

Now the surface Fβ1，β2=F（β1∪β2）is connected or has two components，and when it has two components，denote the two components by X1and X2.

If Fβ1，β2is connected，then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）. So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If Fβ1，β2has two components X1and X2，then Xicontains a cutting section of βjfor i，j=1，2.There are several possibilities as follows.

If the four arcs γ1，γ2，γ3，γ4are pairwise non-isotopic，then there are several possibilities for them.If γi⊂X1（i=1，2，3，4），then we can choose αi（i=1，2）in X1such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1，γ2⊂X1and γ3，γ4⊂X2，then we can choose α1in X1and α2in X2such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2. If γ1，γ3⊂X1and γ2，γ4⊂X2，then there exists an essential arc α in X1connecting γ1and γ3such that α∩αi=α∩βi=ϕ（i=1，2）.Since both β1and β2are nonseparating in F，we can choose αi（i=1，2）such that αi∩β2=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2，γ3⊂X1and γ4⊂X2，then we can choose α1in X1such that α1∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2and γ1，γ3，γ4are pairwise non-isotopic，then there are several possibilities for them.If γi⊂X1（i=1，3，4），then we can choose αi（i=1，2）in X1such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1⊂X1and γ3，γ4⊂X2，then we can choose α1in X1and α2in X2such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2. If γ1，γ3⊂X1and γ4⊂X2，then we can choose α1in X1such that α1∩βi=ϕ（i=1，2）. Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ3and γ1，γ2，γ4are pairwise non-isotopic，then there are several possibilities for them.If γi⊂X1（i=1，2，4），then we can choose αi（i=1，2）in X1such that αi∩βj=ϕ（i，j=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.If γ1⊂X1and γ2，γ4⊂X2，then there exists an essential arc or curve α in X1with α∩αi=α∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose αi（i=1，2）such that αi∩β2=ϕ（i=1，2）.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 3.If γ1，γ2⊂X1and γ4⊂X2，then we can choose α1in X1with α1∩βi=ϕ（i=1，2）.Since β2is nonseparating in X2，we can choose α2such that α2∩β2=ϕ.So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2=γ3and γ1，γ4are pairwise non-isotopic，then similar to the former discussion，we can see that the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

If γ1=γ2=γ3=γ4，then we can choose αi（i=1，2）such that αi∩βj=ϕ（i，j=1，2）. So the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is 2.

In a word，we see that when both β1and β2are essential curves in F，the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is at most 4.

If β1is an essential curve and β2is an essential arc or both of them are essential arcs in F，then similar to the former discussion，we can see that the subsurface 1-distance between｛α1，α2｝and｛β1，β2｝is at most 4.

The proof is completed.

References

［1］Harvey W.Boundary Structure of the Modular Group.Ann.of Math.Studies 97，Riemann Surfaces and Related Topics.Princeton：Princeton Univ.Press，1981：245-251.

［2］Hempel J.3-manifolds as viewed from the curve complex.Topology，2OO1，40：631-657.

［3］Minsky Y.Combinatorial and Geometrical Aspects of Hyperbolic 3-manifolds.in：Komori Y，Markoric V，Series C.Groups and Hyperbolic 3-Manifolds：Lond.Math.Soc.Lec.Notes 299. New York：Cambridge Univ.Press，2OO3：3-4O.

［4］Johnson J，Minsky Y，Moriah Y.Heegaard splittings with large subsurface distances.Algebr. Geom.Topol.，2O1O，10：2251-2275.

［5］Li T.Images of the disk complex.Geom.Dedicata，2O12，158：121-136.

［6］Sun D Q，Lei F C，Li F.Connectedness of curve complex of surface.Sci.China Math.，2O14，57：847-854.

［7］Hempel J.3-Manifold.Annals of Math.Studies 86.Princeton：Princeton Univ.Press，1975.

［8］Masur H，Minsky Y.Geometry of the complex of curves II：Hierarchical structure.Geom.Funct. Anal.，2OOO，10：9O2-974.

1O.13447/j.1674-5647.2O16.O4.O9

date:Dec.14，2015.

The NSF（11426076）of China.

E-mail address:sundq1029@hrbeu.edu.cn（Sun D Q）.

Communicated by Lei Feng-chun