Fock-Sobolev Spaces and Weighted Composition Operators among Them

HE LI AND CAO GUANG-FU

（School of Mathematics，Guangzhou University，Guangzhou，510006）

Fock-Sobolev Spaces and Weighted Composition Operators among Them

HE LI AND CAO GUANG-FU*

（School of Mathematics，Guangzhou University，Guangzhou，510006）

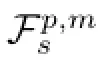
Fock-Sobolev space，dual space，weighted composition operator

2010 MR subject classification:32C37，47B33，47A3O

Document code:A

Article ID:1674-5647（2O16）O4-O3O3-16

1　Introduction

Throughout this paper，let Cnbe the complex n-space and dv be the usual volume measure on Cn.For any points z=（z1，...，zn）∈Cnand w=（w1，...，wn）∈Cn，we denote

Suppose that α=（α1，...，αn）is an n-tuple indices of non-negative integers.Write

For O＜p≤∞，s＞O，set

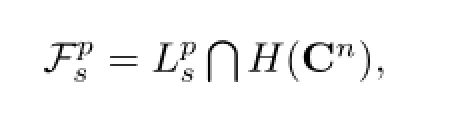
For convenience，we simply denote f≲g or g≳f if there is a positive constant C such that f≤Cg，and f∼g if f≲g and g≲f.

Motivated by some recent ideas by Cho and Zhu［1］，we show the equivalence that‖f‖p，m，s∼‖|w|mf‖p，sin the next section.

Let u and φ be entire functions on Cn.The weighted composition operator uCφis defined by uCφf=u.（f◦φ）for any entire function f.When u=1，the Cφis called a composition operator.

As we known，there are plenty of results concern the boundedness，compactness and Schatten p-class for composition operators and weighted composition operators among several Banach spaces，as a consequence，the norms and essential norms of composition operators and weighted composition operators on these spaces are estimated.For instance，Shapiro［2］gave an equivalent description about the compactness of Cφon Hardy spaces and weighted Bergman spaces，and estimates the essential norm of Cφby using the angular derivative of its inducing map.Cuˇckovi´c and Zhao［3］showed that uCφis bounded on Bergman space L2a（D）if and only if Bφ（|u|2）is bounded on D and uCφis compact if and only if Bφ（|u|2）vanishes to zero at the boundary of D，where D is the open unit disk of the complex plane ℂ and

is the φ-Berezin transform of|u|2.Indeed，for various spaces，the problems of composition operators or weighted composition operators as well as their applications have attracted many other authors:by Roan［4］among Lipschitz spaces，by Smith［5］among Bergman and Hardy spaces，by Zhao［6］from Bloch type spaces to Hardy and Besov spaces，by Tjani［7］among Bloch spaces and Besov spaces，BMOA and VMOA.

Moreover，extensions of many of these conclusions to Fock-type spaces are also obtained. Fock-type spaces，are also called as Bargmann-type spaces or Segal Bargmann-type spaces，have a great deal with quantum mechanics，see［8］and［9］.In recent years，there are abundant results about composition operators and weighted composition operators on these type spaces.Ueki［10］characterizes the boundedness and compactness of weighted composition operators on Fock space Fpα（C）in terms of a certain integral transform，and gets some estimates about the essential norms of uCφ.Stevi´c［11］shows that the similar conclusion still holds in Fock space in the higher-dimensional case.For more details，refer to［12］-［26］.

2　Preliminaries

This section is devoted to doing some preparation work for the later sections，mainly includes equivalently characterizing the Fock-Sobolev space and showing how fast an arbitrary function grows.

Proof.It is similar to the proof of theorem 11 in［1］.Hence，we omit the detail here.

According to the equivalence given above，it is more convenient for us to use the following definition instead of using（1.1）.That is，for O＜p≤∞，we define

with the norm

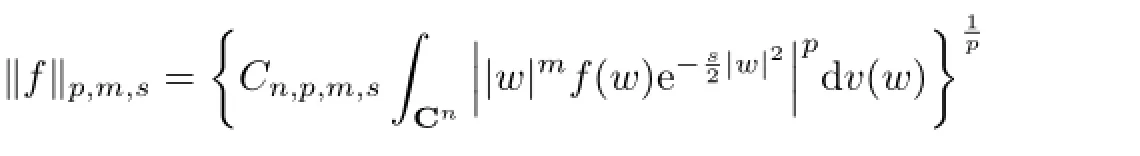
and

where

is the normalizing constant such that‖1‖p，m，s=1.

Lemma 2.2［1］Suppose that O＜p＜∞，O＜r＜∞，O≤a＜∞and O＜b＜∞.Then there exists a positive constant C=C（a，b，r）such that

Lemma 2.3［1］Suppose that O＜p＜∞，O≤a＜∞and O＜b＜∞.Then there exists a positive constant C=C（a，b）such that

∫

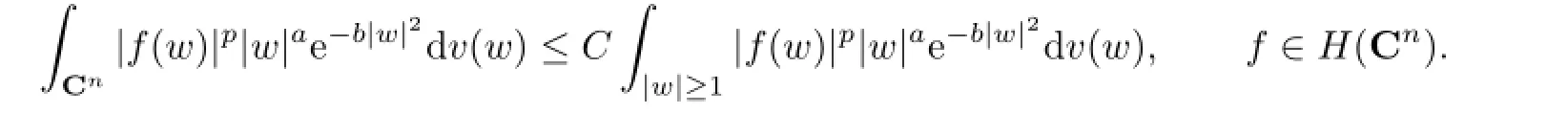
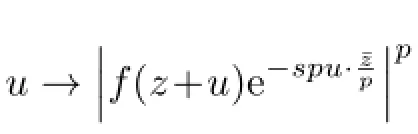
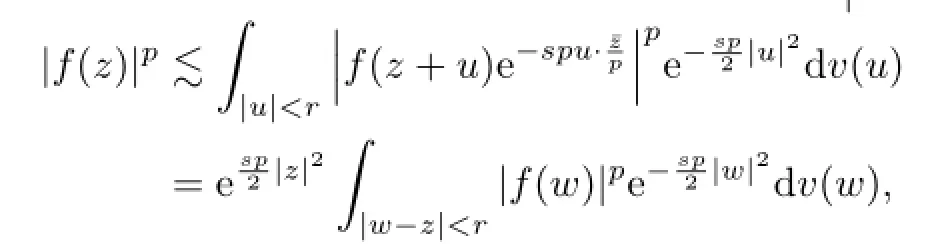
by changing the variable u=w-z，which indicates

since|w-z|＜r yields|z|＜r+|w|.Thus，

This ends the proof.

Next，we introduce two transformations for entire functions on Cn，which were firstly defined by Cho and Zhu［1］.They are

where ckare constants with cm=1，q0=1 and qkis the Taylor polynomial of eλof order k-1 for k≥1.

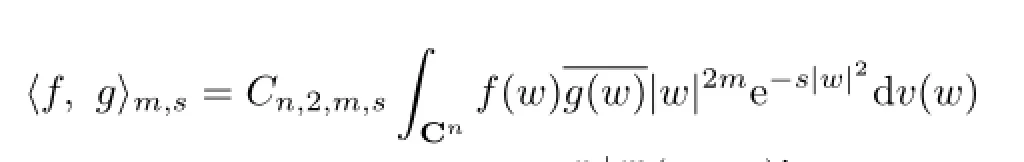
A direct calculation yields

Lemma 2.4Suppose that s＞O and m is a non-negative integer.Then we have

Moreover，

Proof.Just like the proof of Proposition 8 in［1］，it is easy to obtain that

To complete the proof，we still have to show that

Note that

Then we get

and this finishes the proof.

Consequently，it is natural to obtain the following estimates.

Proposition 2.2Suppose that O＜p≤∞，s＞O，m is a non-negative integer and f∈H（Cn）.Then

Proof.It is obvious that

from equality（2.1）and Lemma 2.4.To obtain the latter half，it is enough to prove the case O＜p＜∞because the case p=∞is obvious by the definition of‖.‖∞，m，sand the estimate for|Km，s（z，w）|given in the first half.By direct computation，for O＜p＜∞，we have

3　Weighted Composition Operators among Some Fock-Sobolev Spaces

In this section，we give the framework and the main results of this paper.We are going to study the weighted composition operators among some Fock-Sobolev spaces.

3.1Boundedness and Norm of uCφ

Moreover，we still have

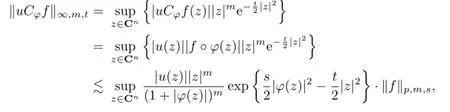
since

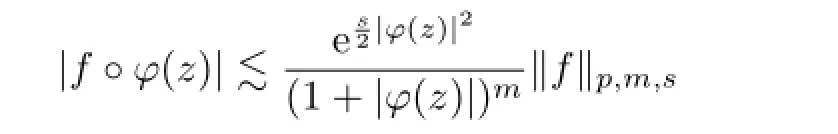
from Proposition 2.1，and this yields

Conversely，set

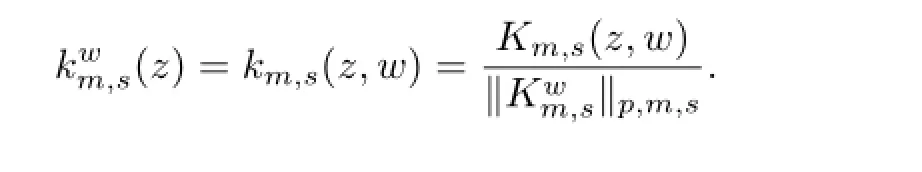
which implies that

Thus，the proof of this theorem is completed.

3.2Compactness and Essential Norm of uCφ

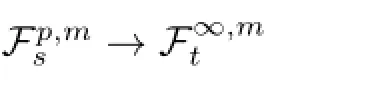
as the Taylor expansion of f.Take

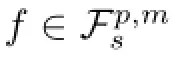
Consequently by the principle of uniform boundedness.The following proposition plays an important role in calculating the essential norm of uCφ.

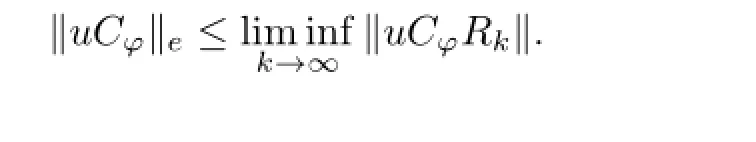
and

Taking the infimum over compact operators K and letting k→∞in（3.1），we get

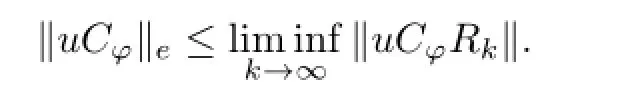
|Rkf（w）|

Proof.Since

by H¨older's inequality，we have

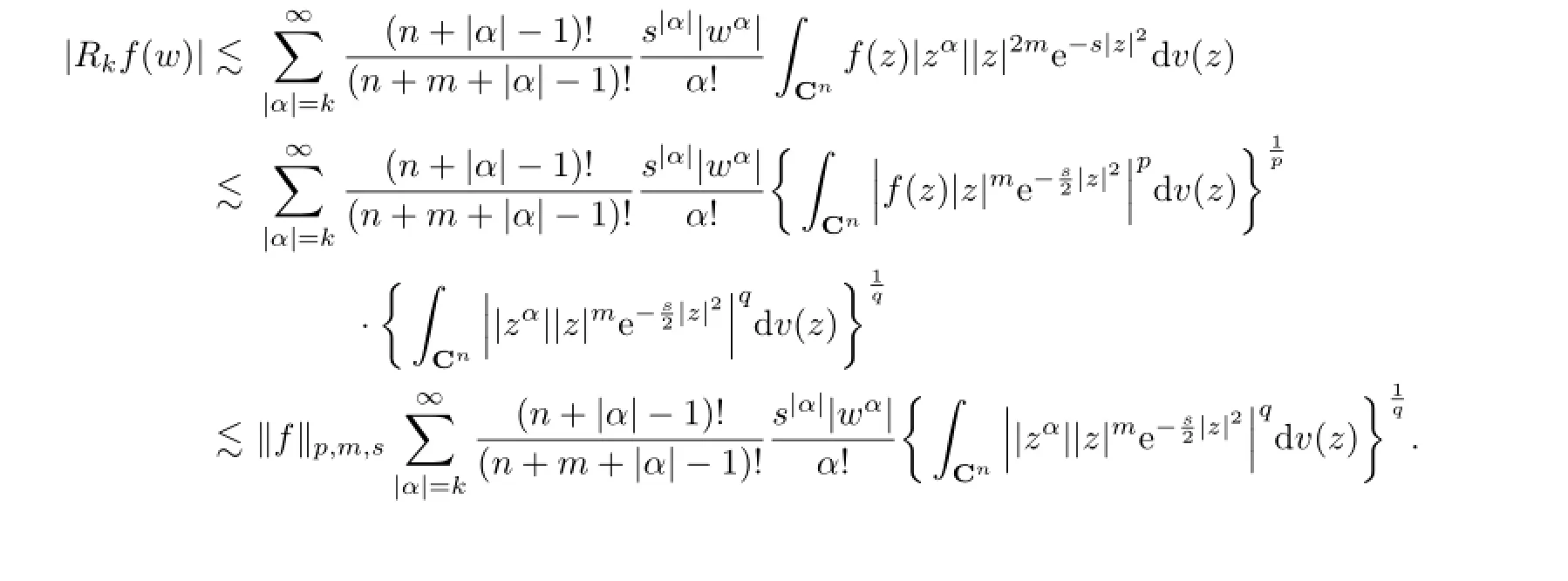
A direct calculation shows that

this yields

|Rkf（w）|

Proof.See Proposition 3.11 of［17］or Proposition 1 of［19］.

Theorem 3.2Suppose that 1＜p＜∞，s＞O，t＞O and m is a non-negative integer.

Further，uCφis compact if and only if

Proof.Firstly，we want to show that

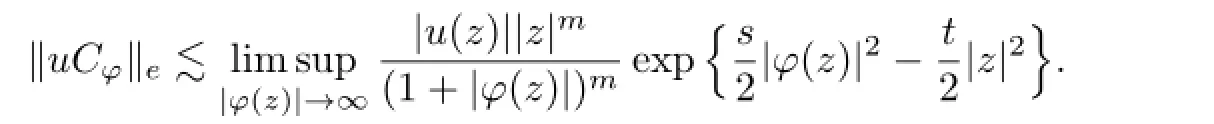
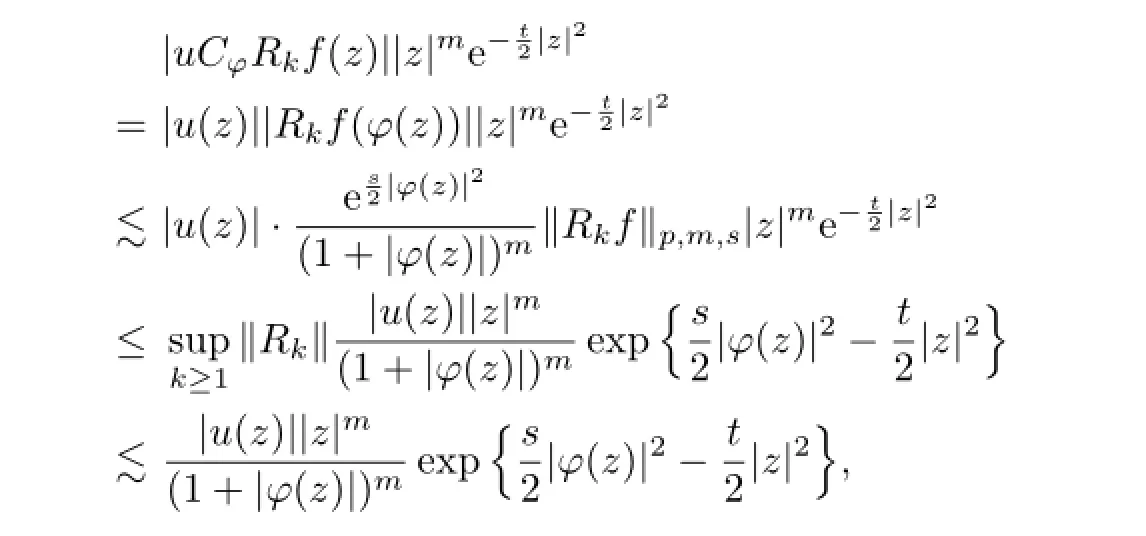
which implies that

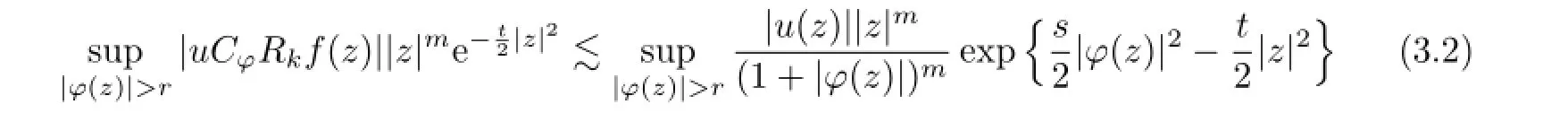
for fixed r＞O.Now，we claim that

In fact，Lemma 3.1 gives

|Rkf（w）|

then

as|α|→∞，where the last equivalence comes from the Stirling's formula.It is not difficult to find the convergence of the series

by using d'Alembert criterion，which implies that

also converges.Thus，we have

as k→∞，and

Combining（3.2），（3.3）and Proposition 3.1，we have

and this yields that

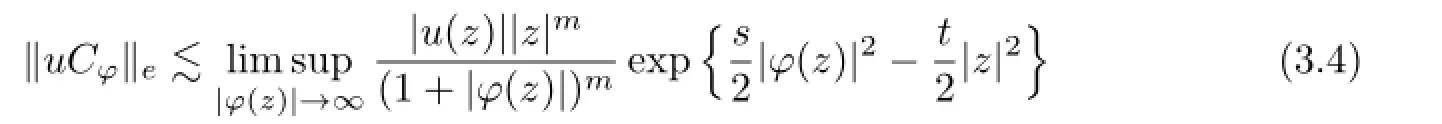
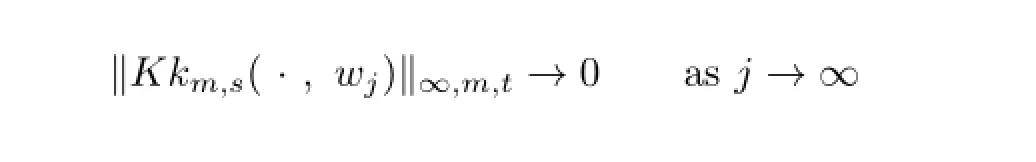
and

Further，we also take a sequence｛zj｝j∈N⊆Cnsuch that φ（zj）→∞as j→∞.Set wj=φ（zj）.Then we get

where the last inequality follows from the proof of Theorem 3.1.This indicates that

Combining（3.4）and（3.5），we obtain

Consequently，uCφis compact if and only if

This ends the proof.

QuestionIs Theorem 3.4 right when p=∞？

4　Duality Space of（O＜p＜∞）

Lemma 4.1Let 1≤p≤∞and Is（z，w）be an integral kernel satisfying the condition

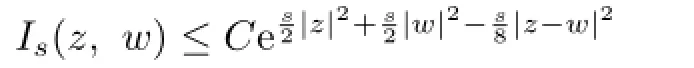
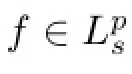
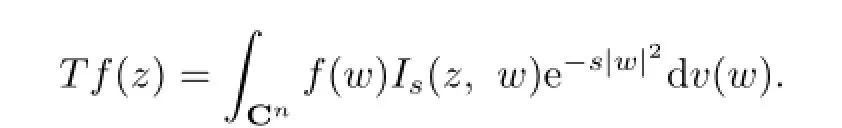
Proof.Similar to the proof of Lemma 9 in［1］.

Consequently，

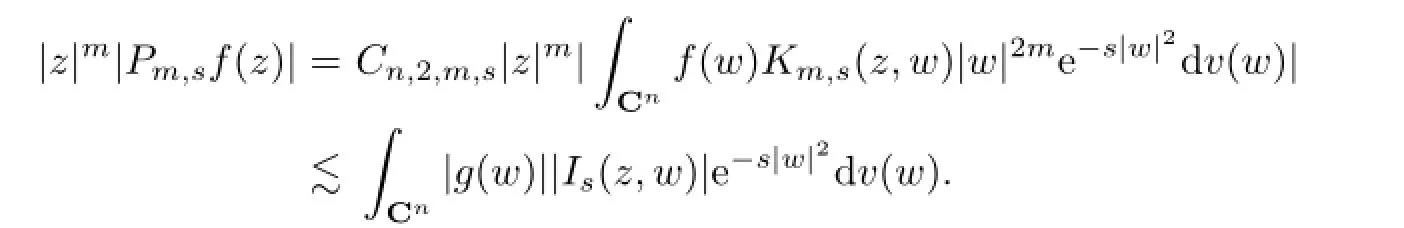
The desired conclusion holds from Lemma 4.1.

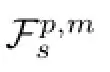
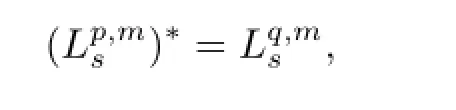
This completes the proof.

Lemma 4.3［1］Suppose that O＜p≤1，O≤a＜∞and O＜b＜∞.Then there exists a positive constant C=C（a，b）such that

for all f∈H（Cn）.

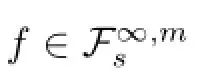
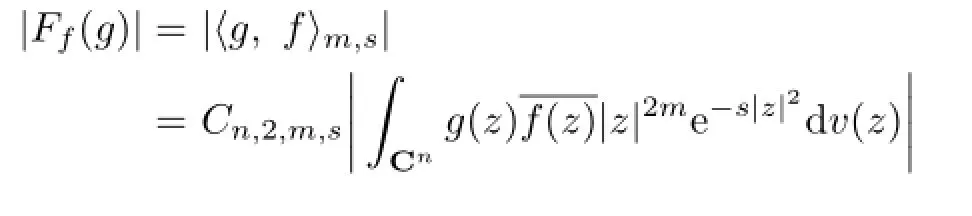
by Proposition 2.2，then

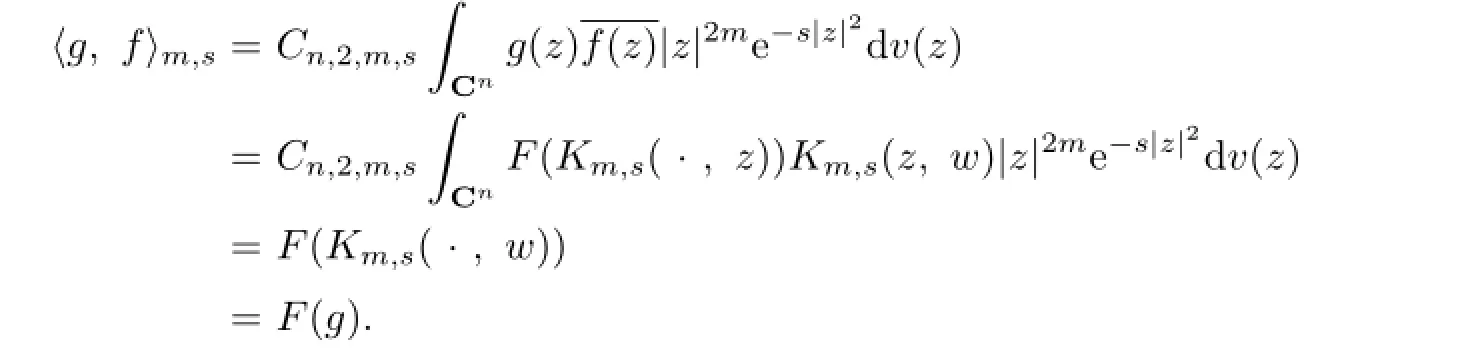
This follows that

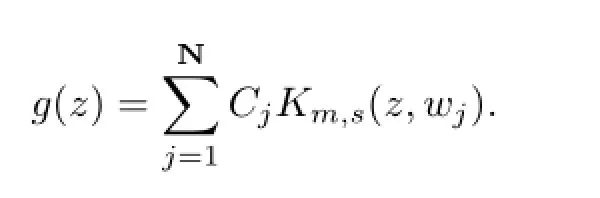
References

［1］Cho H R，Zhu K H.Fock-Sobolev spaces and their Carleson measures.J.Funct.Anal.，2O12，263（8）：2483-25O6.

［2］Shapiro J H.The essential norm of a composition operator.Ann.of Math.，1987，125（2）：375-4O4.

［3］Cuˇckovi´c Z，Zhao R H.Weighted composition operators on the Bergman space.J.London Math.Soc.，2OO4，70（2）：499-511.

［4］Roan R C.Composition operators on a space of Lipschitz functions.Rocky Mountain J.Math.，198O，10（2）：371-379.

［5］Smith W.Composition operators between Bergman and Hardy spaces.Trans.Amer.Math. Soc.，1996，348（6）：2331-2348.

［6］Zhao R H.Composition operators from Bloch type spaces to Hardy and Besov spaces.J.Math. Anal.Appl.，1999，233（2）：749-766.

［7］Tjani M.Compact composition operators on some Moebius invariant Banach spaces.Thesis（Ph.D.），Michigan：Michigan State University，1996.

［8］Berger C A，Coburn L A.Toeplitz operators and quantum mechanics.J.Funct.Anal.，1986，68（3）：273-299.

［9］Berger C A，Coburn L A.Heat flow and Berezin-Toeplitz estimates.Amer.J.Math.，1994，116（3）：563-59O.

［1O］Ueki S.Weighted composition operator on the Fock space.Proc.Amer.Math.Soc.，2OO7，135（5）：14O5-141O.

［11］Stevi´c S.Weighted composition operators between Fock-type spaces in Cn.Appl.Math.Comput.，2OO9，215（7）：275O-276O.

［12］MacCluer B D，Shapiro J H.Angular derivatives and compact composition operators on the Hardy and Bergman spaces.Canad.J.Math.，1986，38（4）：878-9O6.

［13］Shapiro J H.Composition operators and classical function theory.Universitext：Tracts in Mathematics.New York：Springer-Verlag，1993.

［14］Wulan H，Zheng D C，Zhu K H.Compact composition operators on BMOA and the Bloch space.Proc.Amer.Math.Soc.，2OO9，137（11）：3861-3868.

［15］Zhao R H.Essential norms of composition operators between Bloch type spaces.Proc.Amer. Math.Soc.，2O1O，138（7）：2537-2546.

［16］Garling D，Wojtaszczyk P.Some Bargmann spaces of analytic functions.Proceedings of the Conference on Function Spaces，Edwardsville，Lecture Notes in Pure and Applied Mathematics，1995，172：123-138.

［17］Cowen C C，MacCluer B D.Composition operators on spaces of analytic functions.Studies in Advanced Mathematics.Boca Raton，FL：CRC Press，1995.

［18］Zhu K H.Analysis on Fock space.New York：Springer-Verlag，2O12.

［19］Ueki S.Weighted composition operators on some function spaces of entire functions.Bull. Belg.Math.Soc.Simon Stevin，2O1O，17（2）：343-353.

［2O］Isralowitz J，Zhu K H.Toeplitz operators on the Fock space.Integral Equations Operator Theory，2O1O，66（4）：593-611.

［21］Berger C A，Coburn L A.Toeplitz operators on the Segal-Bargmann space.Trans.Amer. Math.Soc.，1987，301（2）：813-829.

［22］Coburn L A，Isralowitz J，Li B.Toeplitz operators with BMO symbols on the Segal-Bargmann space.Trans.Amer.Math.Soc.，2O11，363（6）：3O15-3O3O.

［23］Schuster A P，Varolin D.Toeplitz operators and Carleson measures on generalized Bargmann-Fock spaces.Integral Equations Operator Theory，2O12，72（3）：363-392.

［24］Chen X M，Hou S Z.A Beurling-type theorem for the Fock space.Proc.Amer.Math.Soc.，2OO3，131（9）：2791-2795.

［25］Cho H R，Zhu K H.Holomorphic mean Lipschitz spaces and Hardy-Sobolev spaces on the unit ball.Complex Var.Elliptic Equ.，2O12，57（9）：995-1O24.

［26］Wang X F，Cao G F，Zhu K H.Boundedness and compactness of operators on the Fock space. Integral Equations Operator Theory，2O13，77（3）：355-37O.

1O.13447/j.1674-5647.2O16.O4.O2

date:June 11，2014.

The NSF（11501136，11271092）of China，the Key Discipline Construction Project of Subject Groups Focus on Mathematics and Information Science in the Construction Project（4601-2015）of the High-level University of Guangdong Province，and the Project（HL02-1517）for the New Talent of Guangzhou University.

.

E-mail address:helichangsha1986@163.com（He L），guangfucao@163.com（Cao G F）.

Communicated by Ji You-qing