Two Optimal Inequalities Related to the S´andor-Yang Type Meanand One-parameter Mean

YANG YUE-YINGAND QIAN WEI-MAO

（1.Mechanic Electronic and Automobile Engineering College，Huzhou VocationalTechnical College，Huzhou，Zhejiang，313000）

（2.School of Distance Education，Huzhou Broadcast and TV University，Huzhou，Zhejiang，313000）

Two Optimal Inequalities Related to the S´andor-Yang Type Mean
and One-parameter Mean

YANG YUE-YING1AND QIAN WEI-MAO2

（1.Mechanic Electronic and Automobile Engineering College，Huzhou VocationalTechnical College，Huzhou，Zhejiang，313000）

（2.School of Distance Education，Huzhou Broadcast and TV University，Huzhou，Zhejiang，313000）

In this paper，we establish two optimal the double inequalities for S´andor-Yang type mean and one-parameter mean.

S´andor-Yang type mean，p-th one-parameter mean，Neuman-S´andor mean，second Seiffert mean，inequality

2010 MR subject classification:26E6O，26D2O

Document code:A

Article ID:1674-5647（2O16）O4-O352-O7

1　Introduction

Let p，q∈R and a，b＞O with a/=b.The Stolarsky means Sp，q（a，b）were defined by Stolarsky［1］as

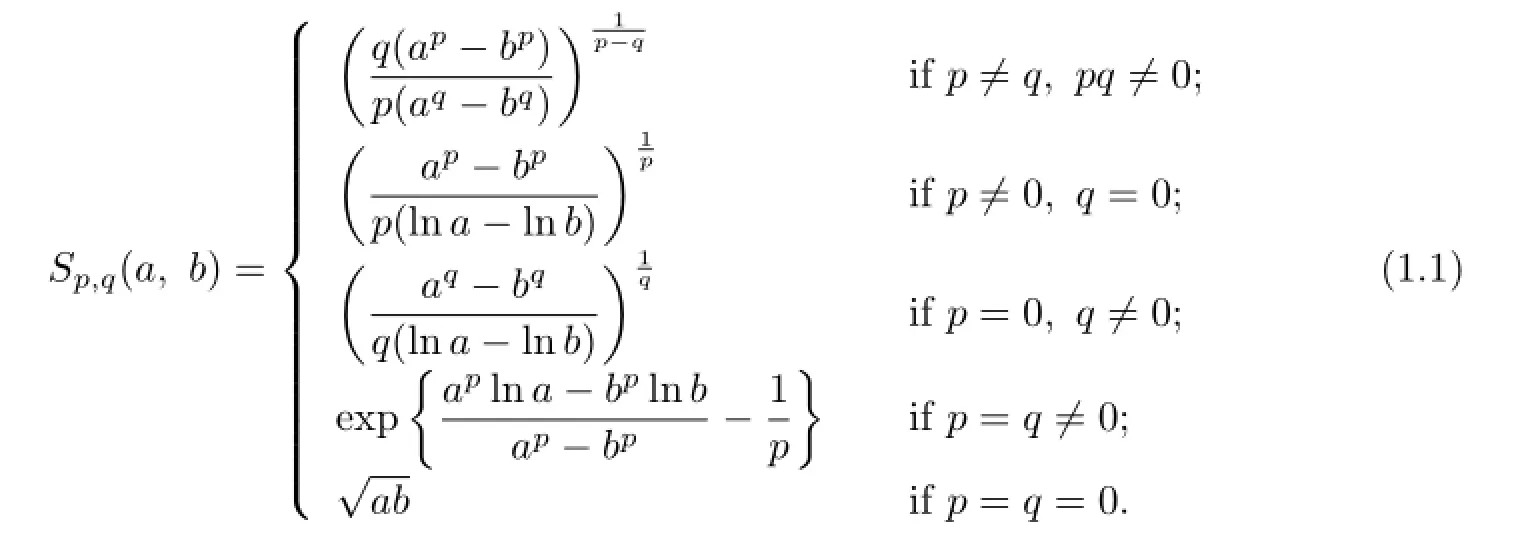
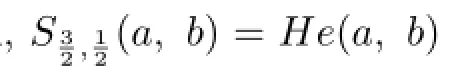
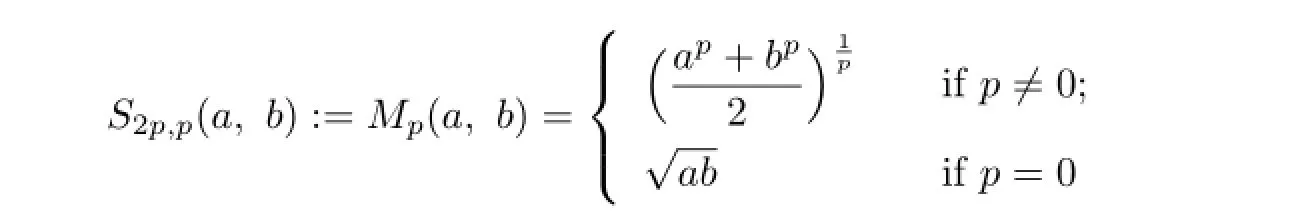
is the p-th power mean of a and b，while

is called the pth one-parameter mean of a and b.

The Schwab-Borchardt mean SB（a，b）of two positive real numbers a and b is defined by

（see［2］-［4］）.It is known that the Schwab-Borchardt mean SB（a，b）is also strictly increasing in both a and b，nonsymmetric and homogeneous of degree one with respect to a and b.Many symmetric bivariate means values are the special cases of the Schwab-Borchardt mean.For instance，

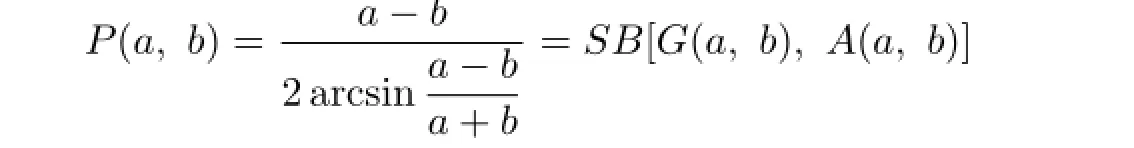
is the first Seiffert mean，

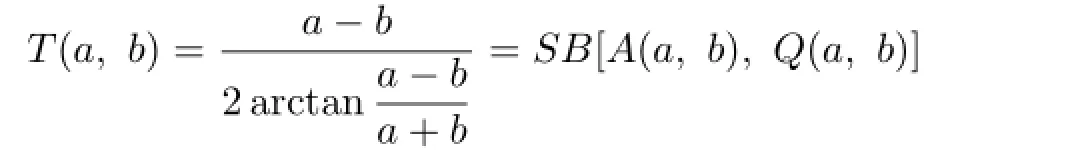
is the second Seiffert mean，

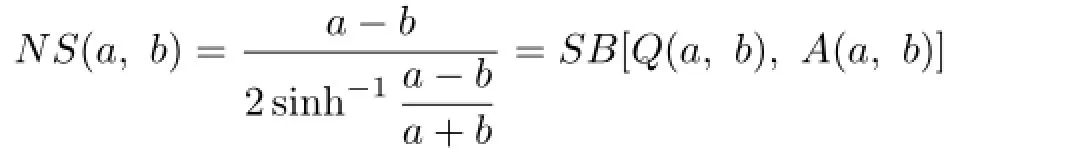
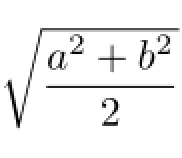
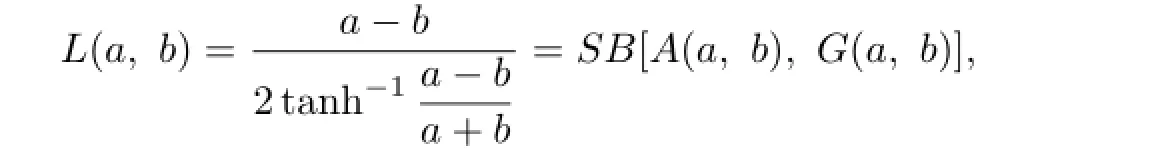
where Q（a，b）= is the quadratic mean.Then it is easy to see that the inequalities

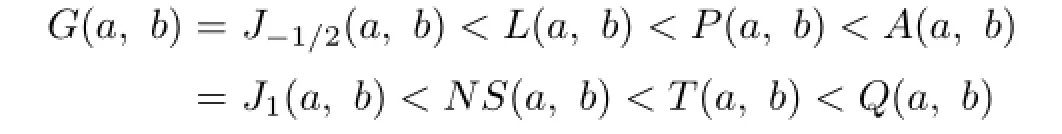
hold for all a，b＞O with a/=b.

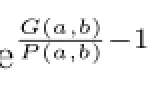
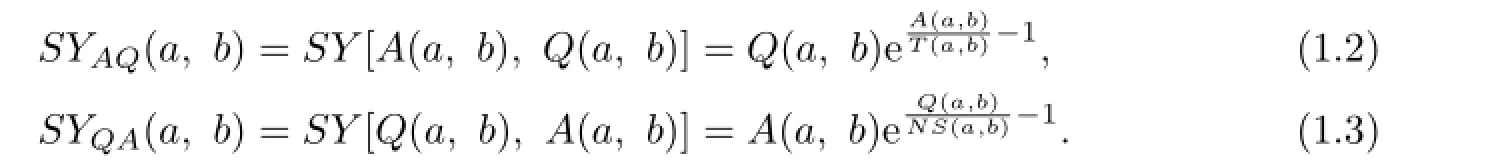
Recently，the one-parameter mean bounds for certain complicated means have attracted attention of some scholars.In［7］，the authors established the following sharp double inequality

hold for all a，b＞O with a/=b.

Gao and Niu［8］gave the best possible parameters p=p（α，β）and q=q（α，β）such that the double inequality

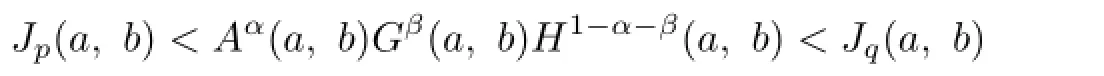
holds for all a，b＞O with a/=b and α，β＞O with α+β＜1.

The main purpose of this paper is to find the best possible parameters α1，α2，β1，β2∈R such that the double inequalities

hold for all a，b＞O with a/=b.

2　Lemmas

In order to prove our main results we need some lemmas which we present in this section.

Lemma 2.1（［9］，Theorems 3.1，3.2）The double inequalities

hold for all a，b＞O with a/=b，where

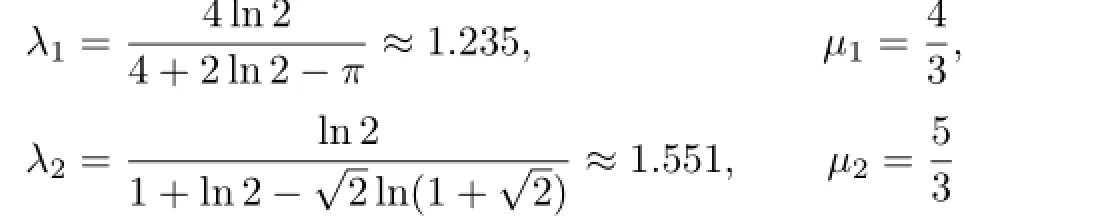
are the best constants.

Lemma 2.2［10］The comparison inequality

holds for all a，b∈R+if and only if

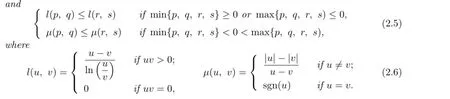
Lemma 2.3For p，q＞O，the inequality

holds for a，b＞O with a/=b if and only if

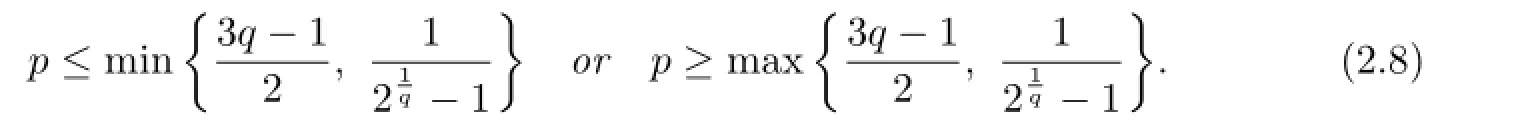
Proof.As mentioned in Introduction，we see that Jp=Sp+1，pand Mp=S2p，p.Then by Lemma 2.2 it is seen that for p，q＞O，the inequality（2.7）holds for a，b＞O with a/=b if and only if

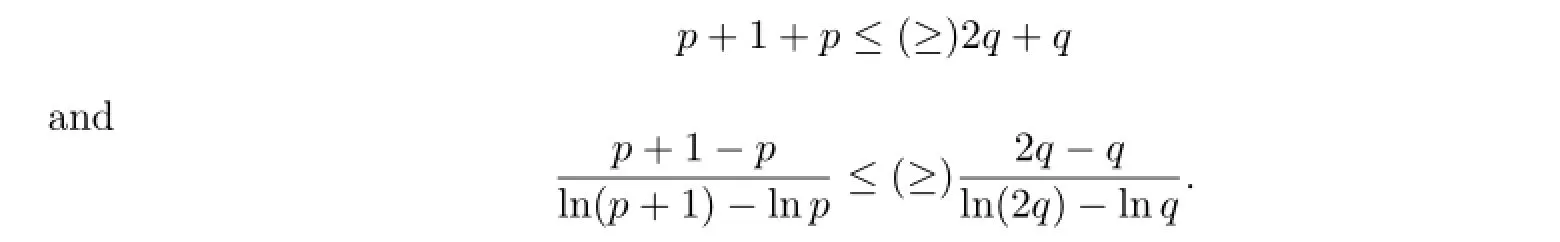
Solving the inequalities for p gives（2.8），which completes the proof.

3　Main Results

Now we are in a position to state and prove our results.

Theorem 3.1The double inequality

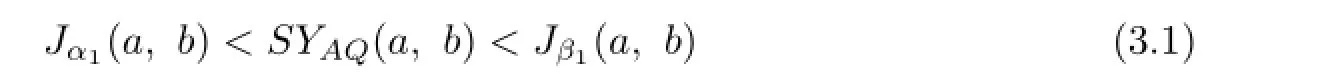
holds for all a，b＞O with a/=b if and only if

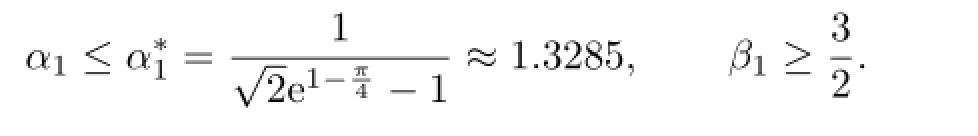
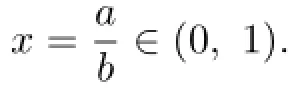
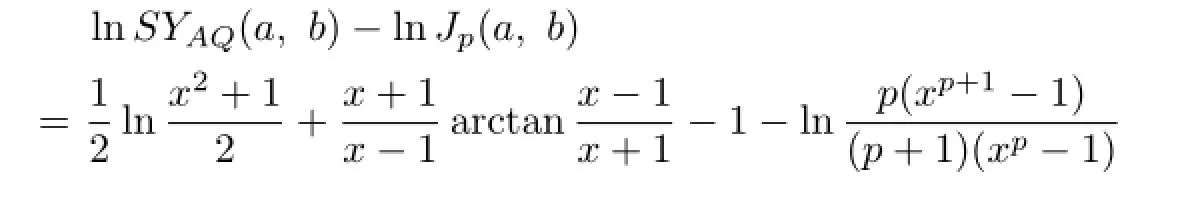
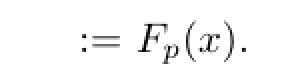
Expanding in power series gives

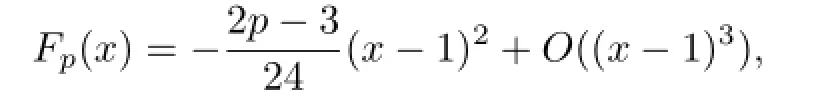
which implies

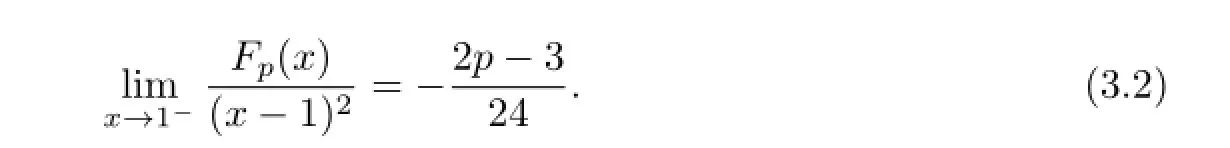
And，a simple computation yields

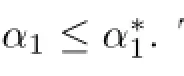
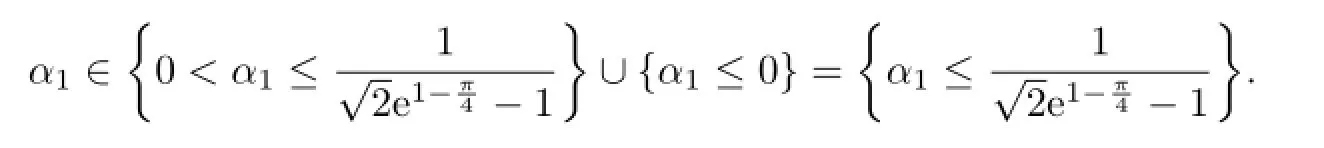
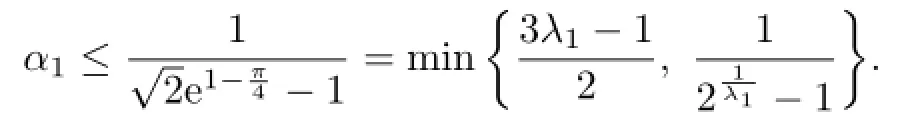
（ii）Similarly，the necessary condition for the right hand side inequality in（3.1）to hold follows from

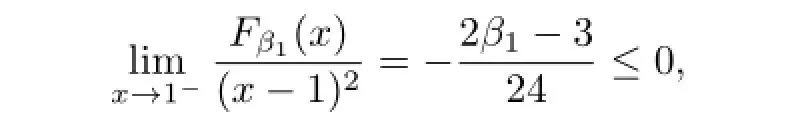
Since

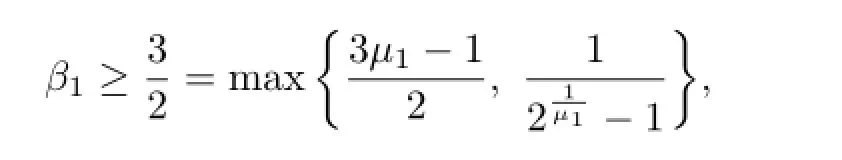
if β1≥3/2，which proves the sufficiency.

Theorem 3.2The double inequality

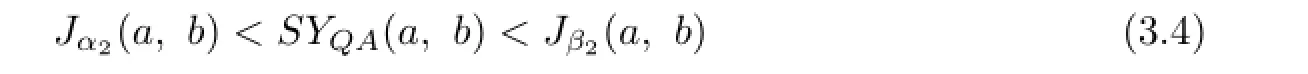
holds for all a，b＞O with a/=b if and only if

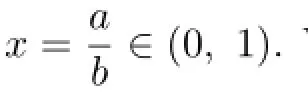
Expanding in power series gives

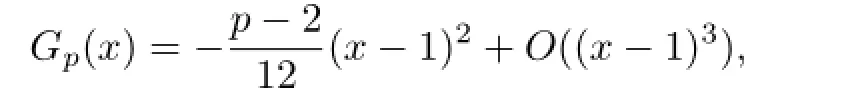
which implies

On the other hand，we easily derive that

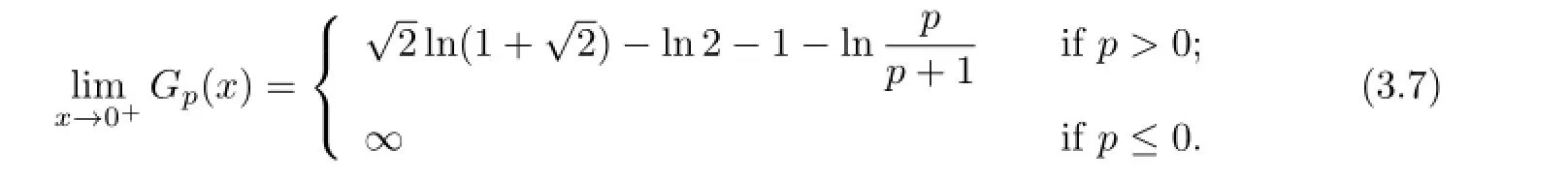
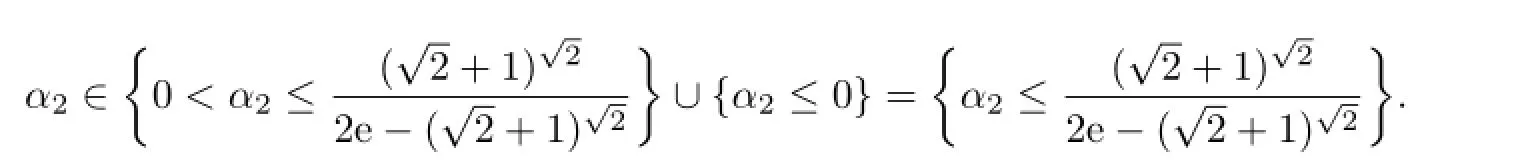
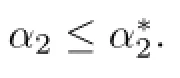
（ii）Likewise，the necessary condition for the right hand side inequality in（3.4）to hold follows from

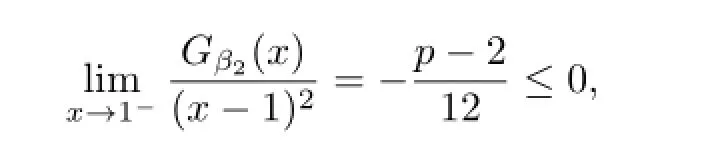
which indicates that β2≥2.

Since

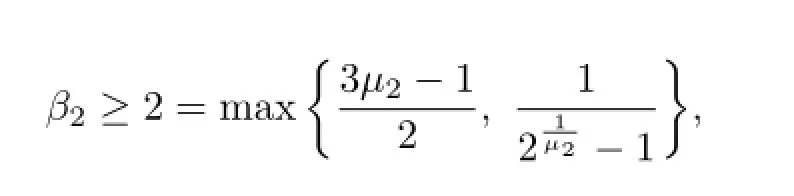
if β2≥2，which proves the sufficiency and the proof is completed.

References

［1］Stolarsky，K.B.Generalizations of the logarithmic mean.Math.Mag.，1975，48：87-92.

［2］Neuman E，S´andor J.On the Schwab-Borchardt mean.Math.Pannon.，2OO3，14（2）：253-266.

［3］Neuman E，S´andor J.On the Schwab-Borchardt mean II.Math.Pannon.，2OO6，17（1）：49-59.

［4］Neuman E.Inequalities for the Schwab-Borchardt mean and their applications.J.Math.Inequal.，2O11，5（4）：6O1-O9.

［5］S´andor J.Two sharp inequalities for trigonometric and hyperbolic function.Math.Inequal. Appl.，2O12，15（2）：4O9-413.

［6］Yang Z H.Three families of two-parameter means constructed by trigonometric functions.J. Inequal.Appl.，2O13，2013，541，27 pages.

［7］Hu H N，Tu G Y，Chu Y M.Optimal bounds for Seiffert mean in terms of one-parameter means.J.Appl.Math.，2O12，2012 Article ID 91712O，7 pages.

［8］Gao H Y，Niu W J.Sharp inequalities reated to one-parameter mean and Gini mean.J.Math. Inequal.，2O12，6（4）：545-555.

［9］Zhao T H，Qian W M，Song Y Q.Optimal bounds for two S´andor-type means in terms of power means.J.Inequal.Appl.，2O16，2016（1）：1-1O.

［1O］P´ales Zs，Inequalities for differences of powers.J.Math.Anal.Appl.，1988，131：271-281.

1O.13447/j.1674-5647.2O16.O4.O7

date:Sept.25，2015.

The NSF（LY13A010004）of Zhejiang Province and the NSF（XKT-15G17）of Zhejiang Broadcast and TV University.

E-mail address:919404713@qq.com（Yang Y Y）.

Communicated by Ji You-qing