The Twin Domination Number of Strong Product of Digraphs

MA HONG-XIA AND LIU JUAN

（College of Mathematics Sciences，Xinjiang Normal University，Urumqi，830017）

The Twin Domination Number of Strong Product of Digraphs

MA HONG-XIA AND LIU JUAN*

（College of Mathematics Sciences，Xinjiang Normal University，Urumqi，830017）

Let γ*（D）denote the twin domination number of digraph D and let D1⊗D2denote the strong product of D1and D2.In this paper，we obtain that the twin domination number of strong product of two directed cycles of length at least 2. Furthermore，we give a lower bound of the twin domination number of strong product of two digraphs，and prove that the twin domination number of strong product of the complete digraph and any digraph D equals the twin domination number of D.

twin domination number，strong product，directed cycle

2010 MR subject classification:O5C69，O5C76

Document code:A

Article ID:1674-5647（2O16）O4-O332-O7

1　Introduction

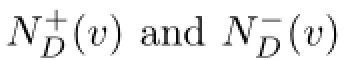
Let D1=（V1，A1）and D2=（V2，A2）be two digraphs，which have disjoint vertex sets V1=｛x1，x2，...，xn1｝and V2=｛y1，y2，...，yn2｝and disjoint arc sets A1and A2，respectively.The strong product D1⊗D2has vertex set V=V1×V2and（xi，yj）（xi′，yj′）∈A（D1⊗D2）if one of the following holds:

（a）xixi′∈A1and yjyj′∈A2；

（b）xi=xi′and yjyj′∈A2；

（c）yj=yj′and xixi′∈A1.

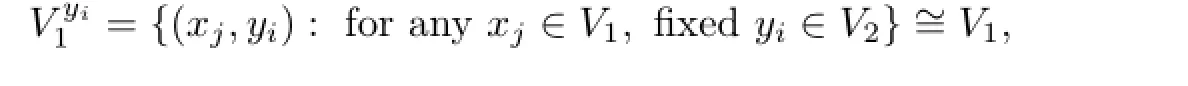
and arc set

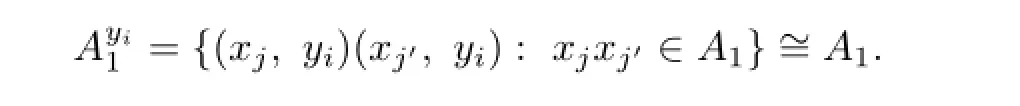
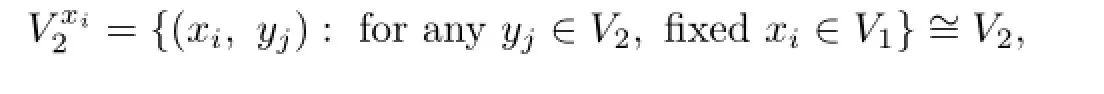
and arc set

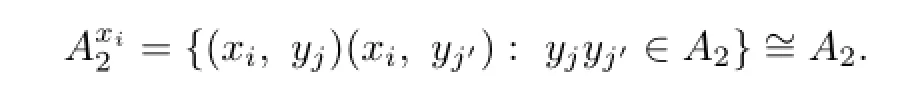
In recent years，the domination number of the cartesian product of directed cycles and paths has been discussed in［2］-［7］.There are some related works for strong product of two digraphs（see，for example，［8］）.In［9］-［15］，it shows the recent related works of twin domination number of digraphs.However，to date no research about twin domination number has been done for strong product of directed cycles.In this paper，we study the twin domination number of Cm⊗Cn.We mainly determine the exact values

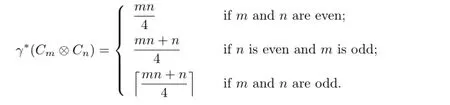
Furthermore，we give a lower bound of γ*（D1⊗D2）and prove that γ*（Km⊗D）=γ*（D）for any digraph D.

2　Main Results

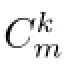
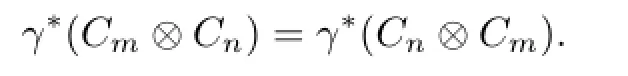
First we investigate the twin domination number of Cm⊗Cn.

Theorem 2.1Let m，n≥2.

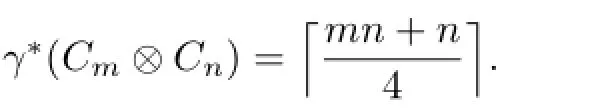
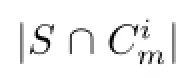
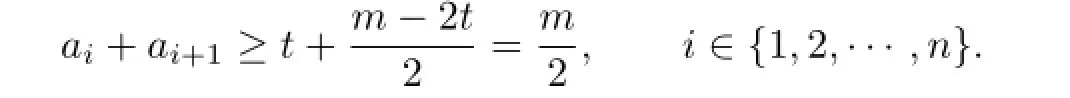
holds yet.

We consider three cases.

Case 1.m and n are even.

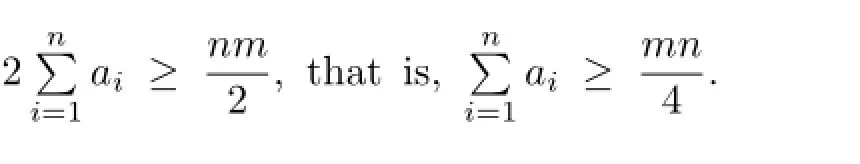
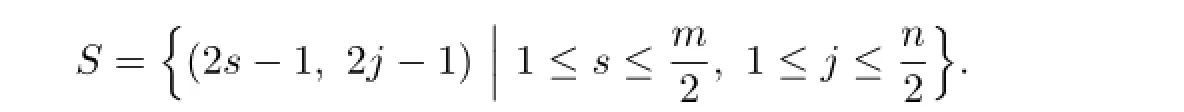
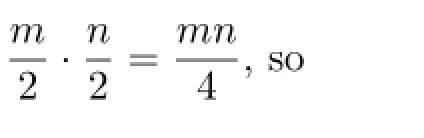
Case 2.m is odd and n is even.

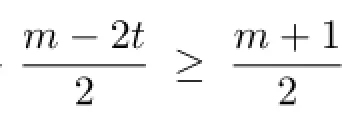
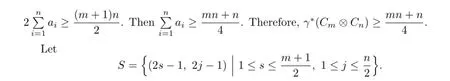
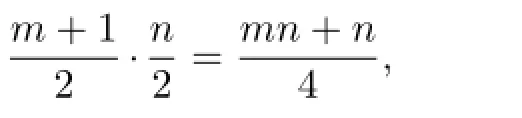
Case 3.m and n are odd.

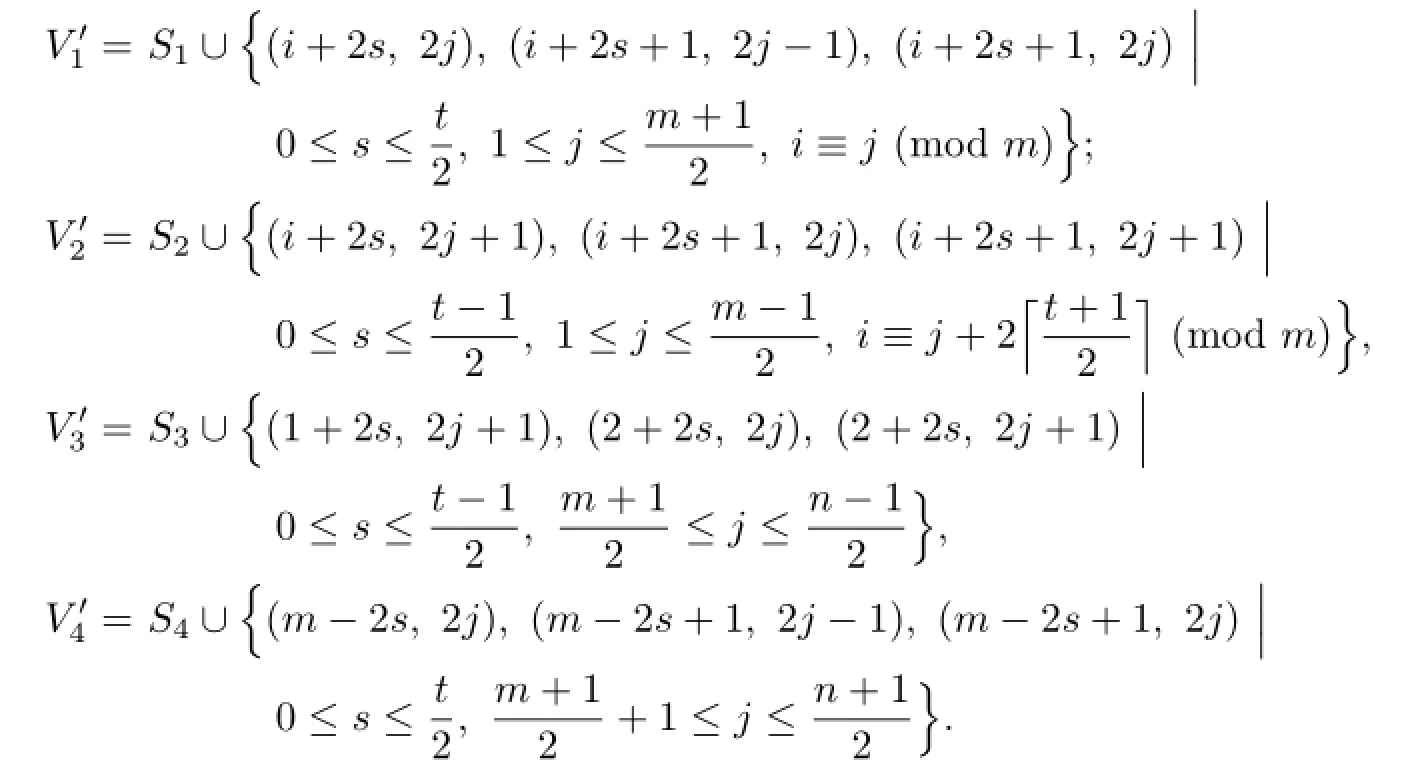
And set

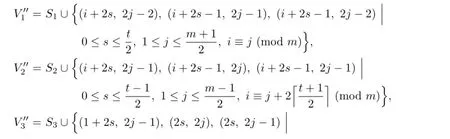
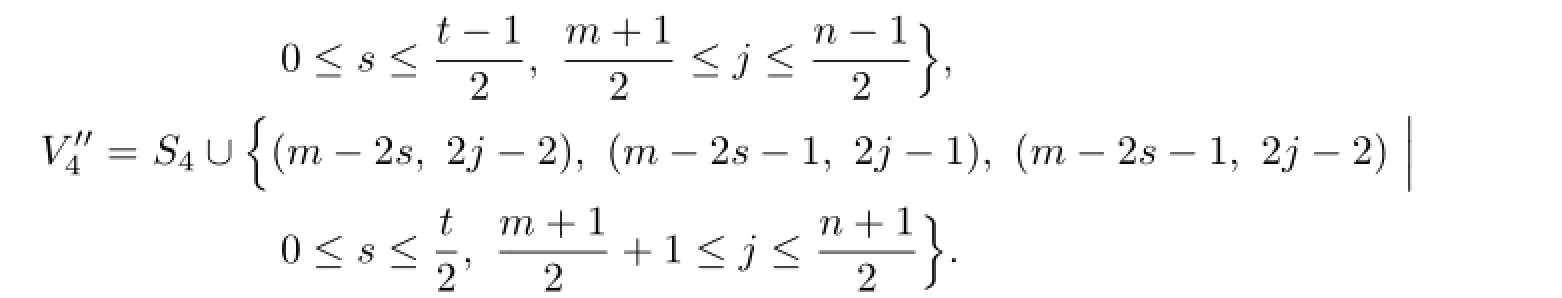
Since m=2t+1，and we consider that t is even，then

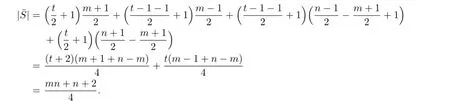
If t is odd，then

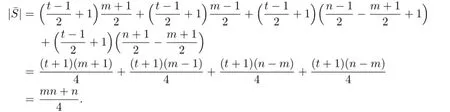
From above all，we have

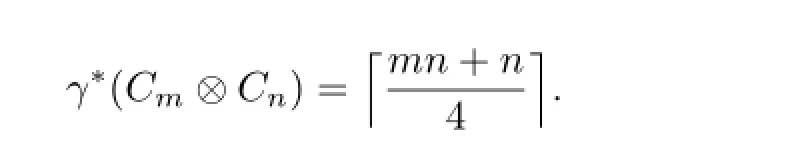
For example，Figs.2.1 and 2.2 show two twin dominating sets of C9⊗C17and C11⊗C17，respectively.

Fig.2.1 A twin dominating set of C9⊗C17（The arcs（i，17）（i+1，1），（i，17）（i，1）and（9，j）（1，j）are omitted，i=（1，...，9），j=（1，...，17））

Fig.2.2 A twin dominating set of C11⊗C17（The arcs（i，17）（i+1，1），（i，17）（i，1）and（11，j）（1，j）are omitted，i=（1，...，11），j=（1，...，19））

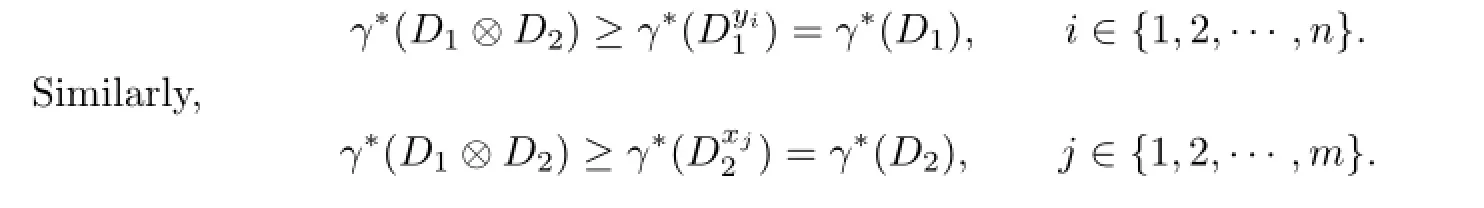
According to the discussion，we can get the following Theorem:

Theorem 2.2For any digraphs D1and D2，we have

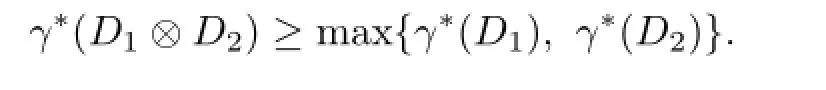
Let

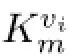
Next，we study the twin domination number of strong product Km⊗D.

Theorem 2.3For any m≥2，we have γ*（Km⊗D）=γ*（D）.

Proof.By Theorem 2.2，we have

Let S be a minimum twin dominating set of D1，and assume

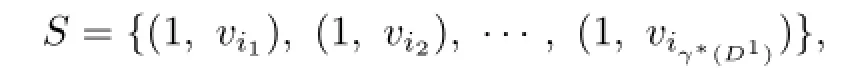
where vi1，vi2，...，viγ*（D1）∈｛v1，v2，...，vn｝.We consider following two cases.

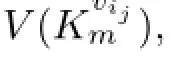
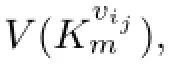
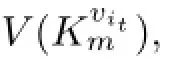
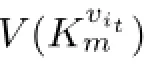
From above all，we conclude that V（Kvitm）are twin dominated by S for every t∈｛1，2，...，n｝.In short，any vertices in Km⊗D are twin dominated by S，and|S|=γ*（D1）= γ*（D）.Hence

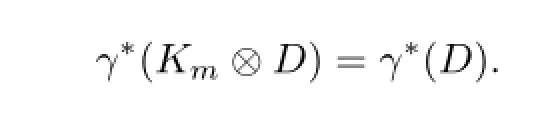
References

［1］Chartrand G，Dankelmann M，Schultz P，Swart H.Twin domination in digraphs.Ars Combin.，2OO3，67：1O5-114.

［2］Shaheen R.Domination number of toroidal grid digraphs.Util.Math.，2OO9，78：175-184.

［3］Liu J，Zhang X D，Chen X，Meng J X.The domination number of Cartesian products of directed cycles.Inform.Process.Lett.，2O1O，110（5）：171-173.

［4］Liu J，Zhang X D，Meng J X.On domination number of Cartesian product of directed path. J.Comb.Optim.，2O11，22（4）：651-662.

［5］Mollard M.On the domination of Cartesian product of directed cycles：Results for certain equivalence classes of lengths.Discuss.Math.Graph Theory，2O13，33（2）：387-394.

［6］Mollard M.The domination number of Cartesian product of two directed paths.J.Comb. Optim.，2O14，27（1）：144-151.

［7］Zhang X D，Liu J，Chen X，Meng J X.On domination number of Cartesian product of directed cycles.Inform.Process.Lett.，2O1O，111（1）：36-39.

［8］Cai H P，Liu J，Qian L.The domination number of strong product of directed cycles.Discrete Math.Algo.Appl.，2O14，6（2）：145OO21（1-1O）.

［9］Arumugan S，Ebadi K，Sathikala L.Twin domination and twin irredundance in digraphs.Appl. Anal.Discrete Math.，2O13，7：275-284.

［1O］Wang Y L.Efficient twin domination in generalized De Bruijin digraphs.Discrete Math.，2O15，338：36-4O.

［11］Araki T.Connected k-tuple twin domination in de Bruijin and Kautz digraphs.Discrete Math.，2OO9，309：6229-6234.

［12］Wu L，Shan E，Liu Z.On the k-tuple domination of generalized de Bruijin and Kantz digraphs. Inform.Sci.，2O1O，180：443O-4435.

［13］Araki T.The k-tuple twin domination in de Bruijin and Kautz digraphs.Discrete Math.，2OO8，308：64O6-6413.

［14］Shan E，Dong Y.The k-tuple twin domination in generalized de Bruijin and Kantz networks. Comput.Math.Appl.，2O12，63：222-227.

［15］Shan E，Dong Y，Cheng Y.The twin domination number in generalized de Bruijn digraphs. Inform.Process.Lett.，2OO9，109（15）：856-86O.

1O.13447/j.1674-5647.2O16.O4.O5

date:April 16，2016.

The NSF（11301450，61363020，11226294）of China，and the Youth Science and Technology Education Project（2014731003）of Xinjiang Province.

.

E-mail address:538254233@qq.com（Ma H X），liujuan1999@126.com（Liu J）.

Communicated by Du Xian-kun