A Generalization of Gorenstein Injective and Flat Modules

LU BO

（1.College of Mathematics and Computer Science，Northwest University for Nationalities，Lanzhou，730030）

（2.Department of Mathematics，Northwest Normal University，Lanzhou，730070）

A Generalization of Gorenstein Injective and Flat Modules

LU BO1，2

（1.College of Mathematics and Computer Science，Northwest University for Nationalities，Lanzhou，730030）

（2.Department of Mathematics，Northwest Normal University，Lanzhou，730070）

In this article，we introduce and study the concept of n-Gorenstein injective（resp.，n-Gorenstein flat）modules as a nontrivial generalization of Gorenstein injective（resp.，Gorenstein flat）modules.We investigate the properties of these modules in various ways.For example，we show that the class of n-Gorenstein injective（resp.，n-Gorenstein flat）modules is closed under direct sums and direct products for n≥2.To this end，we first introduce and study the notions of n-injective modules and n-flat modules.

n-injective module，n-flat module，n-Gorenstein injective module，n-Gorenstein flat module，preenvelope，cover

2010 MR subject classification:16D4O，13E15，16D5O，18G25

Document code:A

Article ID:1674-5647（2O16）O4-O339-13

1　Introduction

Let R be a ring.A left R-module N is called Gorenstein injective if there is a Hom（Inj，-）exact exact sequence

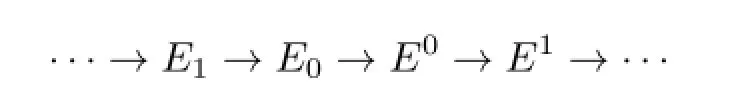
of injective left R-modules such that N=ker（E0→E1），where Inj stands for the class of all injective left R-modules（see［1］）.A right R-module M is called Gorenstein flat if there is a-⊗Inj exact exact sequence of flat right R-modules such that M=ker（F0→F1）（see［2］）.Gorenstein injective and Gorenstein flat modules have been studied by many authors（see［1］-［5］and so on）.These modules have nice properties when the ring in question is n-Gorenstein（a ring R is called n-Gorenstein if R is a left and right Noetherian ring with self-injective dimension at most n for an integer n≥O on either side）.For example，if R is n-Gorenstein and G is a Gorenstein injective left（right）R-module，then G+is a Gorenstein flat right（left）R-module；if R is Gorenstein，then arbitrary products and sums of Gorenstein flat modules are Gorenstein flat.However，these results are not true over general rings（see［6］）.

The main purpose of this paper is to extend some Gorenstein homological properties over Noetherian rings or coherent rings to any ring.To this end，we introduce a generalization of Gorenstein injective（resp.，Gorenstein flat）modules which forms a class closed under direct sums（resp.，direct products）over any ring.These modules are called n-Gorenstein injective（resp.，n-Gorenstein flat）modules.Therefore，although the direct sum（resp.，direct product）of Gorenstein injective（resp.，Gorenstein flat）modules need not be Gorenstein injective（resp.，Gorenstein flat）in general，the direct sum（resp.，direct product）of Gorenstein injective（resp.，Gorenstein flat）modules is always 2-Gorenstein injective（resp.，2-Gorenstein flat）.And an R-module M is-1-Gorenstein injective（-1-Gorenstein flat）if and only if M is Gorenstein injective（Gorenstein flat）.We study the properties of n-Gorenstein injective modules and n-Gorenstein flat modules over any ring.For example，it is shown that a right R-module M is n-Gorenstein flat if and only if there is a-⊗nPI exact exact sequence O→M→F0→F1...with each Fin-flat and Tor1（M，E）=O for all n-presented injective left R-modules E and a left R-module M is n-Gorenstein injective if and only if there is a Hom（nPI，-）exact exact sequence...E1→E0→M→O with each Ein-injective and Ext1（E，M）=O for all n-presented injective left R-modules E，where nPI denotes the class of all n-presented injective left R-modules.We prove that M+is n-Gorenstein flat for any n-Gorenstein injective left R-module M with n≥2 over any ring R.We also show thatRR is n-injective if and only if every left R-module is n-Gorenstein injective.

Let us recall some known notions and facts needed in the sequel.

Let R be a ring and n a nonnegative integer.Following Costa［8］，a left R-module is calledn-presented if it has a finite n-presentation，i.e.，there is an exact sequence

in which each Fiis finitely generated free.Clearly，every finitely generated projective R-module is n-presented for any n≥O.An R-module M is O-presented（resp.，1-presented）if and only if it is finitely generated（resp.，finitely presented）.Every m-presented R-module is n-presented for m≥n.A ring R is called left n-coherent in case every n-presented left R-module is n+1-presented（see［8］）.It is easy to see that R is left O-coherent（resp.，1-coherent）if and only if R is left Noetherican（resp.，coherent），and every n-coherent ring is m-coherent for m≥n.

2　n-injective and n-flat Modules

In this section，in order to introduce and study the notions of n-Gorenstein injective modules and n-Gorenstein flat modules，we first introduce and investigate the concepts of n-injective modules and n-flat modules.

Let R be a ring.A left R-module M is called-1-presented，that is，the class of all -1-presented modules denotes the category of all left R-modules.

Definition 2.1Let n be an integer with n≥-1.A ring R is called left n-coherent if any n-presented left R-module is n+1-presented.

Remark 2.1If n≥O，then the left n-coherent ring is just the n-coherent ring which is introduced by Costa［8］.

Definition 2.2Let n be an integer.A left R-module M is said to be n-injective if Ext1（P，M）=O for every n-presented left R-module P.A right R-module N is called n-flat if Tor1（N，P）=O for every n-presented left R-module P.

Remark 2.2（1）It is clear that a left R-module M is-1-injective or O-injective（resp.，1-injective）if and only if M is injective（resp.，FP-injective）.A right R-module N is-1-flat，O-flat or 1-flat if and only if N is flat.

（2）Every n-injective（resp.，n-flat）module is m-injective（resp.，m-flat）for any n≤m. If R is n-coherent，then an R-module M is n-injective（resp.，n-flat）if and only if M is m-injective（resp.，m-flat）for n≤m.

（3）A ring R is coherent if and only if any n-flat（n≥2）module is flat.A ring R is Noetherian if and only if any n-injective（n≥1）module is injective by the following Theorem 2.2.

Lemma 2.1［9］（1）Let A be an n-presented left R-module with n≥2 and（Mi）i∈Ia direct system of right R-modules（with I directed）.Then

（2）Let A be an n-presented right R-module with n≥2 and（Ni）i∈Ia family of right R-modules.Then

It is well known that an R-module M is flat if and only if M+is injective，and if R is coherent，then a left R-module M is injective if and only if M+is flat.Here we have the following result over general rings.

Theorem 2.1Let R be a ring and n≥-1 an integer.Then

（1）A right R-module M is n-flat if and only if M+is n-injective；

（2）A left R-module M is n-injective if and only if M+is n-flat for n≥2.

Proof.（1）It follows from the isomorphism Ext1（N，M+）∼=Tor1（M，N）+for any left R-module N.

（2）Note that Tor1（M+，P）∼=Ext1（P，M+）for any left R-module M and any 2-presented left R-module P by Lemma 2.1.Hence M is n-injective if and only if M+is n-flat.

The proof is completed.

From Theorem 2.1，it is easy to see that if M is injective，then M+need not be flat. However，M+is n-flat（n≥2）.

As we know，the direct product of flat modules is not necessarily flat and the direct limit of injective modules need not be injective in general.Here we give an interesting result establishing the transfer of the n-flatness to the direct product and the n-injectivity to the direct limit.

Theorem 2.2Let R be a ring and n≥-1 an integer.Then

（1）Every direct product of n-injective left R-modules is n-injective；

（2）Every direct limit（resp.，sum）of n-injective left R-modules is n-injective for any n≥2（resp.，n≥1）；

（3）Every direct sum of n-flat right R-modules is n-flat；

（4）Every direct product of n-flat right R-modules is n-flat for any n≥2；

（5）A left R-module M is n-injective if and only if M++is n-injective for any n≥2；（6）A right R-module M is n-flat if and only if M++is n-flat for any n≥2.

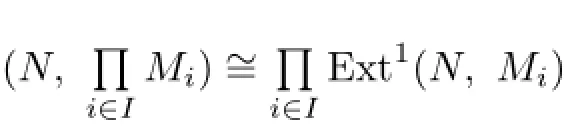
（5）Since M+is n-flat if and only if M++is n-injective by Theorem 2.1，then M is n-injective if and only if M++is n-injective for n≥2 by Theorem 2.1 again.

（6）If M is an n-flat right R-module，then M+is n-injective.So M++is n-flat for n≥2 by Theorem 2.1.Conversely，if M++is n-flat，then M+is n-injective for n≥2 by Theorem 2.1.Hence M is n-flat.

The proof is completed.

From Theorem 2.2，it is clear that n-injective（resp.，n-flat）modules are the nontrivial generalization of injective（resp.，flat）modules for n≥2.

Proof.Let N be a pure submodule of an n-injective left R-module M.For any n-presented left R-module P，we have the exact sequence

But the sequence Hom（P，M）→Hom（P，M/N）→O is exact since P is n-presented with n≥1 and N is a pure submodule of M，so Ext1（P，N）=O.Therefore，N is n-injective.

Let N be a pure submodule of an n-flat right R-module M.Then the exact sequence O→N→M→M/N→O induces the split exact sequence O→（M/N）+→M+→N+→O.Thus N+is n-injective since M+is n-injective by Theorem 2.1.So N is n-flat by Theorem 2.1 again.

Lemma 2.2（［6］，Proposition 5.2.2）If F is a class of R-modules closed under direct sums，then an R-module M has an F-precover if and only if there is a cardinal number Nαsuch that any homomorphism D→M with D∈F has a factorization D→C→M with C∈F and Card（C）≤Nα.

Lemma 2.3（［1O］，Theorem 5）Let R be an arbitrary ring.Then for each cardinal λ，there is a cardinal κ such that for any R-module M and any L≤M satisfying Card（M）≥κ and Card（M/L）≤λ，the submodule L contains a nonzero submodule that is pure in M.

Lemma 2.4（［6］，Corollary 5.2.7）Let F be a class of R-modules that is closed under well ordered inductive limits and M be an R-module.If M has an F-precover，then it has an F-cover.

The following result is essentially due to Lemma 2.5 in［11］.For completeness we include a proof.

Theorem 2.3Let R be a ring and n≥2 an integer.Then

（1）Every right R-module has an Fn-preenvelope；

（2）Every left R-module has an In-cover.Proof.（1）Let M be any right R-module.By Lemma 5.3.12 in［6］，there is a cardinal number Nαsuch that for any homomorphism f:M→L with L n-flat，there is a pure submodule P of L such that Card（P）≤Nαand f（M）⊆P.Note that P is n-flat by Proposition 2.1，and so M has an Fn-preenvelope by Theorem 2.2 and Proposition 6.2.1 in［6］.

If Card（E）≤κ，then we are done.Hence we may assume Card（E）＞κ.

Let K=ker（f）.Note that Card（E/K）≤λ since E/K embeds in N.Then K contains a nonzero submodule E0which is pure in E by Lemma 2.3，and so the pure exact sequence O→E0→E→E/E0→O induces the split exact sequence O→（E/E0）+→E+→E+0→O.Thus（E/E0）+is n-flat since E+is n-flat by Theorem 2.1.So E/E0is n-injective by Theorem 2.1 again.

If Card（E/E0）≤κ，then we are done by Lemma 2.2 since f factors through E/E0.

Suppose Card（E/E0）＞κ.Put

Theorem 2.4Let R be a ring and n≥-1 an integer.Then

Lemma 2.5Let R be a ring and n≥-1 an integer.

（1）Let M be a left R-module.If Ext1（P，M）=O for any n-presented left R-module P，then Ext2（F，M）=O for any n+1-presented left R-module F；

（2）Let M be a right R-module.If Tor1（M，P）=O for any n-presented left R-module P，then Tor2（M，F）=O for any n+1-presented left R-module F.

Proof.（1）Let F be an n+1-presented left R-module.Then we have an exact sequence

where Q is finitely generated projective and K is n-presented.This induces an exact sequence

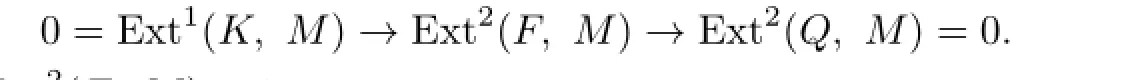
Hence we have Ext2（F，M）=O.

（2）Let F be an n+1-presented left R-module.Then we have an exact sequence

where Q is finitely generated projective and K is n-presented.This induces an exact sequence

So we have Tor2（M，F）=O.

Theorem 2.5Let R be an n-coherent ring and n≥1 an integer.Then

Proof.（1）It is clear that any injective left R-module is n-injective and B is n-injective for any exact sequence O→A→B→C→O with A and C are n-injective by the definition of n-injective modules.We now claim that C is n-injective for any exact sequence O→A→B→C→O with A and B are n-injective.For any n-presented left R-module P，the exact sequence O→A→B→C→O induces the exactness of Ext1（P，A）→Ext1（P，B）→Ext1（P，C）→Ext2（P，A）.On the other hand，Ext2（P，A）=O since Ext1（P，A）=O by Lemma 2.5.Thus Ext1（P，C）=O since Ext1（P，B）=O.So C is n-injective.

（2）The proof is similar to that of（1）.

3　n-Gorenstein Injective and n-Gorenstein Flat Modules

Lemma 3.1［9］The following statements are equivalent for a right R-module M:

（1）M is finitely presented；

（3）τ:M⊗RΛ→MΛis an isomorphism for any set Λ.

Lemma 3.2（［9］，Exercise 1.2.2）Let M be an R-module and（Ni）i∈Ibe a family of R-modules.If M is finitely generated，then

Now we introduce the following definitions:

Definition 3.1Let R be a ring and n≥-1 an integer.A left R-module N is said to be n-Gorenstein injective if there is an exact sequence

of n-injective left R-modules such that N=ker（E0→E1）and for any n-presented injective left R-module E，Hom（E，-）leaves the complex above exact.

Definition 3.2Let R be a ring and n≥-1 an integer.A right R-module M is said to be n-Gorenstein flat if there is an exact sequence

of n-flat right R-modules such that M=ker（F0→F1）and for any n-presented injective left R-module E，-⊗E leaves the complex above exact.

Remark 3.1（1）If...→E-1→E0→E1→...is a Hom（E，-）（resp.，-⊗E）exact exact sequence with E n-presented injective and Ein-injective（resp.，n-flat）for any i∈Z，then every ker（Ei→Ei+1）and coker（Ei→Ei+1）are n-Gorenstein injective（resp.，n-Gorenstein flat）.

（2）Let R be a ring.It is clear that a left R-module M is-1-Gorenstein injective if and only if M is Gorenstein injective；a right R-module N is-1-Gorenstein flat if and only if N is Gorenstein flat.

（3）By the definitions，it is obvious that every n-Gorenstein injective（resp.，flat）module is m-Gorenstein injective（resp.，flat）for any m≥n≥-1.However，the converse is not true in general（see Theorem 3.1）.If R is n-coherent，then an R-module M is n-Gorenstein injective（resp.，flat）if and only if M is m-Gorenstein injective（resp.，flat）for any m≥n≥-1.

It is an important question to investigate the direct sum and direct product of modules. It is well known that the direct sum of injective left R-modules is injective if and only if R is left noetherican；the direct product of flat left R-modules is flat if and only if R is left coherent（see［14］）；if R is Gorenstein，then arbitrary products and sums of Gorenstein flat modules are Gorenstein flat.However，it is not true in general（see［6］）.In 2OO6，Christensen et al.［15］proved that if R is commutative and Noetherian with a dualizing complex，then direct product of Gorenstein flat modules is Gorenstein flat.Here we give an interesting result establishing the transfer of the Gorenstein flatness to the direct product and the Gorenstein injectivity to the direct limit over general rings.

Theorem 3.1The following statements are true for any ring R:

（1）Every direct sum of n-Gorenstein flat right R-modules is n-Gorenstein flat；（2）Every direct product of n-Gorenstein injective left R-modules is n-Gorenstein injective；（3）Every direct sum（resp.，limit）of n-Gorenstein injective left R-modules is n-Gorenstein injective for n≥1（resp.，n≥2）；

（4）Every direct product of n-Gorenstein flat right R-modules is n-Gorenstein flat for n≥2.

（3）Let（Mi）i∈Ibe a family of n-Gorenstein injective left R-modules with n≥1.Then there is an exact sequence

is an exact sequence of n-injective left R-modules with n≥1 by Theorem 2.2.

For any n-presented injective left R-module E with n≥1，we have

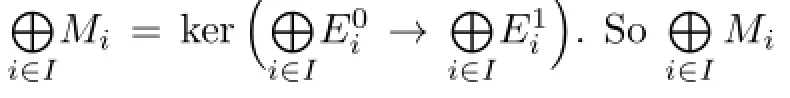
injective.

（4）The proof is similar to that of（3）.

The proof is completed.

In what follows，nPI denotes the class of all n-presented injective left R-modules.

Lemma 3.3Let R be a ring.

（1）If M is an n-Gorenstein injective left R-module，then Ext1（E，M）=O for all n-presented injective left R-modules；

（2）If M is an n-Gorenstein flat right R-module，then Tor1（M，E）=O for all n-presented injective left R-modules.

Proof.（1）By the hypothesis，there is a Hom（nPI，-）exact exact sequence

with each Eiinjective.Thus Ext1（E，M）=O for all n-presented injective left R-module E by definitions.

（2）The proof is similar to that of（1）.

Proposition 3.1Let R be a ring and n≥-1 an integer.Then

（1）a right R-module M is n-Gorenstein flat if and only if there is a-⊗nPI exact exact sequence with each Fin-flat and Tor1（M，E）=O for all n-presented injective left R-modules E；

（2）a left R-module M is n-Gorenstein injective if and only if there is a Hom（nPI，-）exact exact sequence

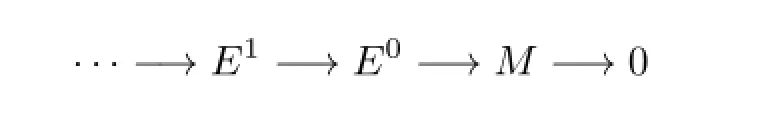
with each Ein-injective and Ext1（E，M）=O for all n-presented injective left R-modules E.

Proof.（1）⇒.It is clear by Lemma 3.3 and the definition of n-Gorenstein flat modules.⇐.Since every right R-module has an Fn-cover by Theorem 2.4，we have an exact sequence

For the short exact sequence

which induces an exact sequence

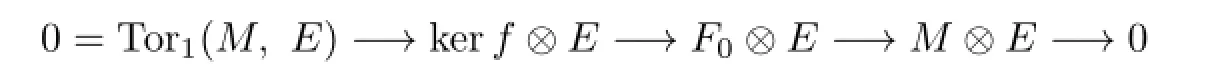
for any n-presented injective left R-module E.Hence M is n-Gorenstein flat by definitions.

（2）The proof is similar to that of（1）by Lemma 3.3 and the definition of n-Gorenstein injective modules.

Proposition 3.2Let R be a ring and n≥-1 an integer.Then

（1）A left R-module M is n-Gorenstein injective if and only if there exists an exact sequence O→N→E→M→O with E n-injective and N n-Gorenstein injective；

（2）A right R-module N is n-Gorenstein flat if and only if there exists an exact sequence O→N→E→M→O with E n-flat and M n-Gorenstein flat.

Proof.（1）⇒.It is clear by definition.

⇐.There is an exact sequence O→N→E→M→O with E n-injective and N n-Gorenstein injective.Then we get an exact sequence...→E1→E0→N→O，where Eiis n-injective.Thus we have an exact sequence

and the sequence（3.1）is Hom（nPI，-）exact.So M is n-Gorenstein injective.

（2）It is similar to the proof of（1）.

The proof is completed.

It is well known that if R is m-Gorenstein and G is a Gorenstein injective left（right）R-module with m≥O an integer，then G+is a Gorenstein flat right（left）R-module（see［6］）.However，here we have the similar results over any ring.

Theorem 3.2Let R be a ring and n an integer.

（1）If M is an n-Gorenstein flat right R-module with n≥-1，then M+is n-Gorenstein injective；

（2）If M is an n-Gorenstein injective left R-module with n≥2，then M+is n-Gorenstein flat.

Proof.（1）By hypothesis，we have a-⊗nPI exact sequence

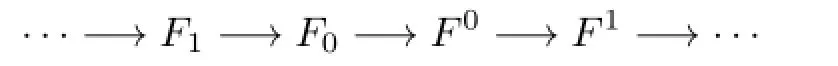
of n-flat right R-modules such that

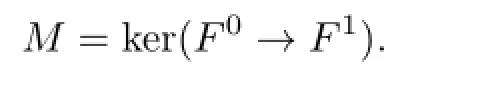
This induces an exact sequence

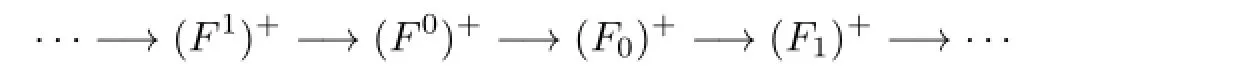
of n-injective left R-modules.It is clear that

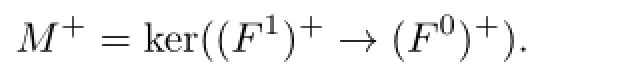
For any n-presented injective left R-module N，the exact sequence

gives the exactness of

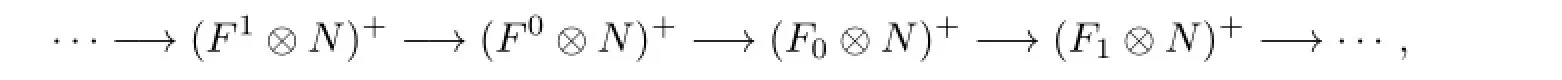
which，in turn，yields the exact sequence

...→Hom（N，（F1）+）→Hom（N，（F0）+）→Hom（N，（F0）+）→Hom（N，（F1）+）→... So M+is n-Gorestein injective.

（2）By hypothesis and Proposition 3.1，we have a Hom（nPI，-）exact exact sequence

with each Ein-injective and Ext1（E，M）=O for all n-presented injective left R-modules E.Thus we get an exact sequence

since Tor1（kerf）+，E）∼=Ext1（E，kerf）+for any n-presented injective left R-module E with n≥2.And so

is a-⊗nPI exact exact sequence.Continuing this process，we have

is a-⊗nPI exact exact sequence.Hence M+is n-Gorenstein flat.

The proof is completed.

As we know，a ring R is semisimple if and only if every R-module is injective.Here we haveRR is n-injective if and only if every left R-module is n-Gorenstein injective.

Theorem 3.3The following statements are equivalent for any ring R and n≥2 an integer:

（1）RR is n-injective；

（2）Every left R-module has an epic n-injective cover；

（3）Every right R-module has a monic n-flat preenvelope；

（4）Every left R-module is n-Gorenstein injective.

Proof.（1）⇒（2）.Let M be a left R-module.Then M has an n-injective cover g.On the other hand，there is an exact sequence F→M→O with F free.Since F is n-injective by（1），g is an epimorphism.

（2）⇒（1）.Let f:N→RR be an epic n-injective cover.ThenRR is isomorphic to a direct summand of N，and soRR is n-injective.

（1）⇒（3）.Let M be any right R-module.Since（RR）+is a cogenerator of R-modules category，there exists an exact sequence O→M→∏（RR）+.Then（RR）+is n-flat by（1）and Theorem 2.1.Thus∏（RR）+is n-flat by Theorem 2.2，and so M embeds in an n-flat right R-module.Every right R-module has a monic n-flat preenvelope since every right R-module has an n-flat preenvelope.

（3）⇒（1）.By（3），RR+embeds in an n-flat right R-module，so（RR）+is n-flat.HenceRR is n-injective.

（2）⇒（4）.Let M be any left R-module.By（2），we have the following Hom（nPI，-）exact exact sequence

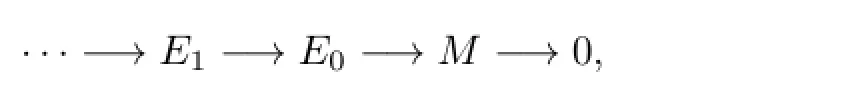
where Eiis n-injective for i≥O.And it is clear that for any left R-module M，we have Hom（nPI，-）exact exact sequence

with Ein-injective for i≥O.So we have Hom（nPI，-）exact exact sequence

with Eiand Ein-injective for i≥O such that M=ker（E0→E1）.Hence M is n-Gorenstein injective.

（4）⇒（1）.Since every left R-module is n-Gorenstein injective，we get an exact sequence O→C→E→R→O with E n-injective.But O→C→E→R→O is split since R is projective.So R is n-injective.

The proof is completed.

A right R-module M is called copure flat if Tor1（M，E）=O for all injective left R-modules E（see［16］）.

Proposition 3.3Let R be a ring and n≥2 an integer.IfRR is n-injective，then every copure flat right R-module is n-Gorenstein flat.

Proof.Let M be a copure flat right R-module.Then Tor1（M，E）=O for any injective left R-module E.On the other hand，we have an exact sequencesuch that Fiand Fin-flat for i≥O and M=ker（F0→F1）.We apply-⊗E to the above sequence with E n-presented injective.Then

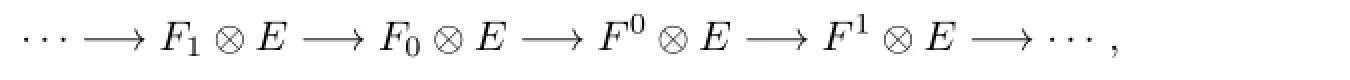
since Tor1（M，E）=O.So M is n-Gorenstein flat.

References

［1］Enochs E E，Jenda O M G.Gorenstein injective and Gorenstein projective modules.Math.Z.，1995，220：611-633.

［2］Enochs E E，Jenda O M G，Torrecillas B.Gorenstein flat modules.Nanjing Univ.J.Math. Biquarterly，1993，10：1-9.

［3］Enochs E E，Jenda O M G，Xu J.Covers and envelopes over Gorenstein rings.Tsukuba J. Math.，1996，20：487-5O3.

［4］Holm H.Gorenstein homological dimensions.J.Pure Appl.Algebra，2OO4，189：167-193.

［5］Sazeedeh R.Gorenstein injective，Gorenstein flat modules and section functor.J.Pure Appl. Algebra，2OO7，211：773-783.

［6］Enochs E E，Jenda O M G.Relative Homological Algebra GEM 3O.Berlin-New York：Walter de Gruyter，2OOO.

［7］Enochs E E.Injective and flat covers，envelopes and resolvents.Israel J.Math.，1981，39：189-2O9.

［8］Costa D L.Parameterizing families of non-noetherian rings.Comm.Algebra，1994，22：3997-4O11.

［9］Chen J L，Ding N Q.On n-coherent rings.Comm.Algebra，1996，24：3211-3216.

［1O］Bican L，El Bashir R，Enochs E E.All modules have flat covers.Bull.London Math.Soc.，2OO1，33：385-39O.

［11］Pinzon K R.Absolutely pure modules.Ph.D.Thesis，University of Kentucky，USA，2OO5.

［12］Eklof P C，Trlifaj J.How to make Ext vanish.Bull.London Math.Soc.，2OO1，33（1）：41-51.

［13］Trlifaj J.Covers，envelopes，and cotorsion theories.Lecture notes for the workshop.Homological Methods in Module Theory.Cortona，September 1O-16，2OOO.

［14］Rotman J J.An Introduction to Homological Algebra.New York：Academic Press，1979.

［15］Christensen L W，Frankild A，Holm H.On Gorenstein projective，injective and flat dimensions—A functorial description with applications.J.Algebra，2OO6，302：231-279.

［16］Enochs E E，Jenda O M G.Copure injective modules.Quaest.Math.，1991，14：4O1-4O9.

1O.13447/j.1674-5647.2O16.O4.O6

date:April 17，2015.

The NSF（11501451）of China，the Fundamental Research Funds（31920150038）for the Central Universities and XBMUYJRC（201406）.

E-mail address:lubo55@126.com（Lu B）.

Communicated by Du Xian-kun