Bayesian Estimation for the Order of INAR（q）Model

MIAO GUAN-HONG AND WANG DE-HUI

（School of Mathematics，Jilin University，Changchun，130012）

Bayesian Estimation for the Order of INAR（q）Model

MIAO GUAN-HONG AND WANG DE-HUI*

（School of Mathematics，Jilin University，Changchun，130012）

In this paper，we consider the problem of determining the order of INAR（q）model on the basis of the Bayesian estimation theory.The Bayesian estimator for the order is given with respect to a squared-error loss function.The consistency of the estimator is discussed.The results of a simulation study for the estimation method are presented.

INAR（q）model，Bayesian estimation，squared-error loss function，consistency

2010 MR subject classification:62F15，62M1O

Document code:A

Article ID:1674-5647（2O16）O4-O325-O7

1　Introduction

The time series models are widely used in many fields and there is a growing interest in time series.Estimating the order of these models is an important part when dealing the data.Chen［1］gave the Bayesian estimator for the orders of AR models with a squarederror loss function.Wang［2］discussed the problem of determining the orders of AR（k）and ARMA（p，q）models of time series on the basis of the Bayesian estimate theory.Peng［3］took advantage of the Bayesian factor to discuss the problem of selecting the order of AR models. Peng［4］gave the Bayesian estimation of the order for MA model.

The first INAR（1）model was introduced by Al-Osh and Alzaid［5］.The INAR（1）model is as follows:

Define the INAR（q）process｛Yt｝by

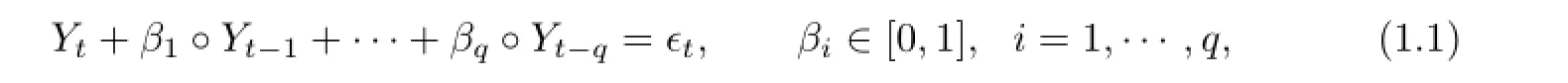
where M is the upper bound.

The INAR（q）process can be expressed as

Based on Theorem 2.2.2 in［6］，the INAR（q）model defined above is also equivalent to the following model:

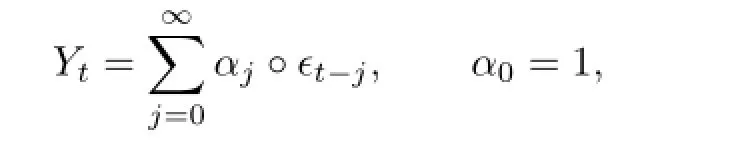
where|αj|≤cρ-j，j≥O，c and ρ are positive constants.Furthermore，we have

The INAR（q）model above can be expressed as

The paper provides the Bayesian approach for the order of INAR（q）model under the assumption that the loss function is the squared-error loss function and the order is a discrete type random variable and has an upper bound.In Section 2，the relationship of the parameters of the INAR（q）model is discussed.The Bayesian estimator for the order is given and its strong consistency is discussed in Section 3.Finally，in Section 4，some simulation results are given to prove the consistency.

2　Property of INAR（q）

The mean of the model｛Yt｝is simply

Based on［7］，

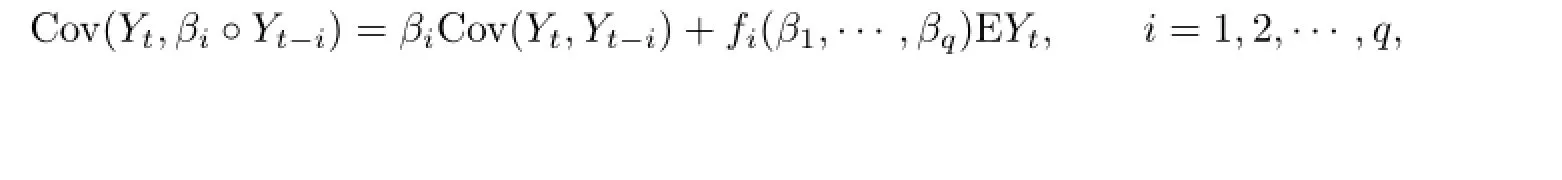
where fi（β1，...，βq）is the function of β1，...，βq.

Let

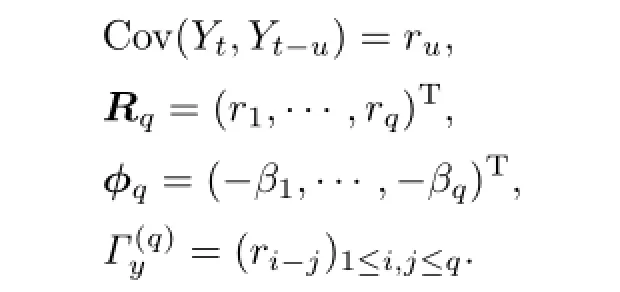
Similarly to the property of AR（q）process，we conclude

Based on［6］and the equation above，we obtain that

the conclusion is

Let

We obtain

3　Bayesian Estimation for the Order

Let Yn=（y1，y2，...，yn）Tdenote the observation sequence from｛Yt｝.Based on［8］，we have

Let

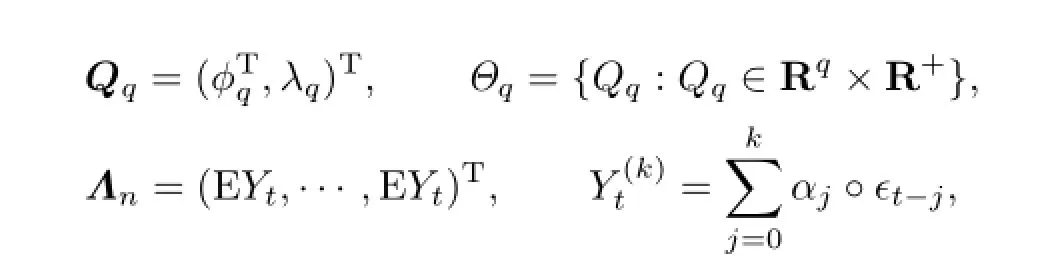
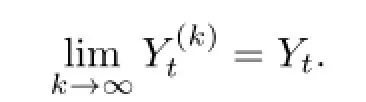
By Levy-Lindberg central limit theorems，｛Yt｝is an normal distribution random sequence，where its conditional probability density function is

Suppose that Ql's conditional probability density function P｛Ql|l｝is consistent when q=l，where

where C is a positive constant.

The loss function is

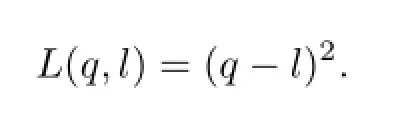
The criteria is defined as

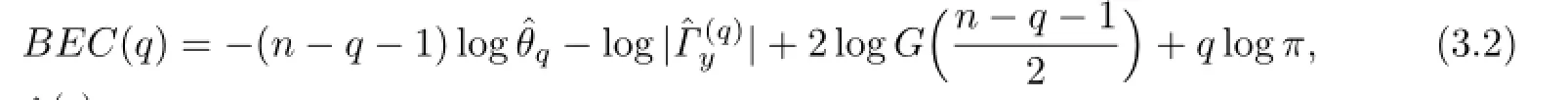
where and G（x）is a gamma function.Let

Lemma 3.1As n→∞and q≥q0（q0is the real order），one has

and as n→∞and q≤q0（q0is the real order），one has

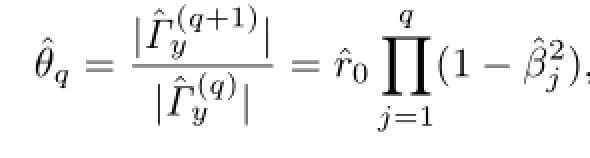
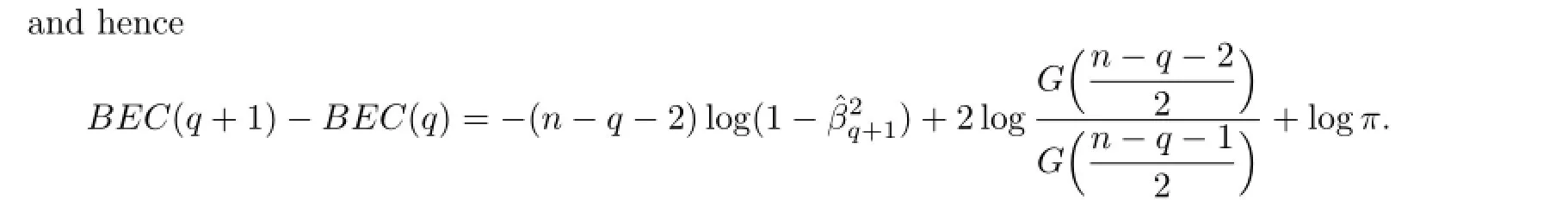
Based on［1］，we obtain

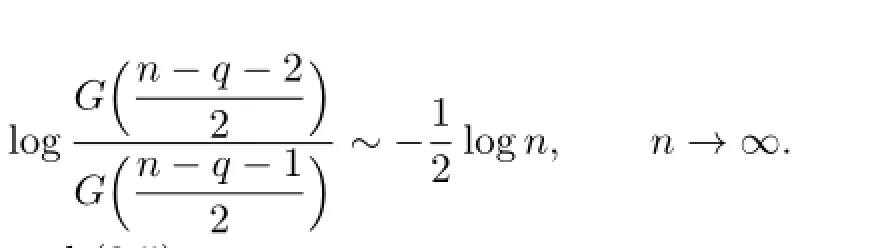
Thus we conclude（3.4）and（3.5）.

Lemma 3.2B（l）defined as（3.1）and T（l）defined as（3.3）have the same minimum point.

Proof.Let H（l）=B（l）L（Yn），where L（Yn）is the probability density function of Yn. P（Qq|q）is the conditional probability density function of Qq.Then B（l）and H（l）have the same minimum point.

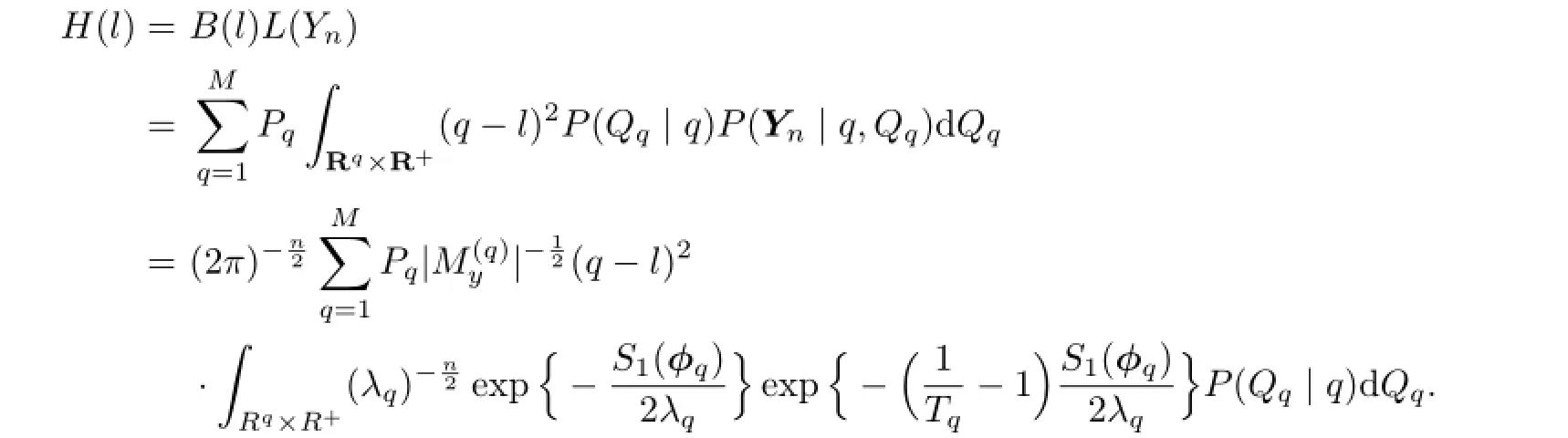
According to［1］，we obtain

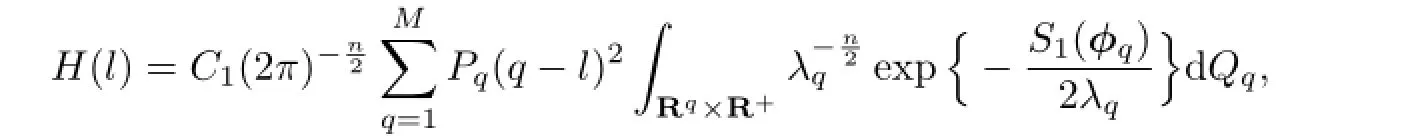
where C1is a constant.

Because

we have

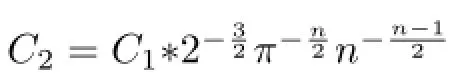
where BEC（q）is defined as（3.2） is independent of l（Yn）.Thus the minimum point of B（l）is equivalent to the minimum point of T（l）.

Let

We obtain

Then the Bayes estimator is

Theorem 3.1Yn=（y1，y2，...，yn）Tis the observation sequence from the model（1.1）and q0is the real order and satisfies 1≤q0≤M，where M is a positive integer and a constant.Thenˆq defined as（3.6）is the strong consistent estimator of the real order q0.

Proof.（1）As l≥q0，let

By Lemma 3.1，as q≥q0，

Thus l could not be the minimum point of BEC（q）when l＞q0.

By Lemma 3.1，as q≤q0，

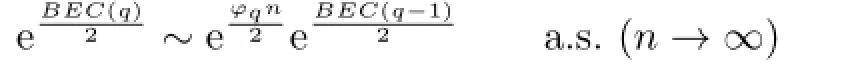
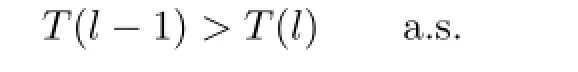
Thus l could not be the minimum point of BEC（q）when l＜q0.This completes the proof of Theorem 3.1.

4　Simulation

We give the simulation result for the following model:

Table 4.1Frequency distribution of the Bayes estimator

Based on the data in the Table 4.1，the estimator is more likely to access the real order as n→∞.We can conclude that the Bayes estimator is consistent.

References

［1］Chen J X.The Bayesian estimator of the orders of AR models of time series with a squared-error loss function（in Chinese）.Chinese J.Appl.Probab.Statist.，1991，7（2）：113-124.

［2］Wang W Y.The Bayesian estimater of the orders of AR（k）and ARMA（p，q）models of time series（in Chinese）.Acta Math.Appl.Sin.，1984，7（2）：185-195.

［3］Peng J L，Liu C H，Wang J.Select the order of AR models by a Bayesian factor method（in Chinese）.Journal of Hubei University of Technology，2OO7，22（1）：13-15.

［4］Peng J L，Ding L P，Wang J.The Bayesian estimation of the order for MA model（in Chinese）. J.Guizhou Univ.（Natur.Sci.），2OO8，25（1）：27-32.

［5］Al-Osh M A，Alzaid A A.First-order integer-valued autoregressive（INAR（1））process.J.Time，2OO8，8（3）：261-275.

［6］Chang X J，Chen M，Wang M S.Time Series Analysis（in Chinese）.Beijing：Higher Education Press，1993.

［7］Alzaid A A，Al-Osh M A.An integer-valued pth-order autoregressive structure（INAR（p））process.J.Appl.Probab.，199O，27（2）：314-324.

［8］Zhang H X.Statistical Inference for RCINAR（1）Model Based on Negative Binomial Thinning Operator（in Chinese）.Master Degree Thesis.Changchun：Jilin University，2OO9.

［9］Zhang H X.Statistical Inference for Integer-valued Time Series and Multivariate Panel Count Data（in Chinese）.Doctoral Dissertation.Changchun：Jilin University，2O12.

1O.13447/j.1674-5647.2O16.O4.O4

date:Jan.4，2015.

.

E-mail address:m653296@163.com（Miao G H），wangdh@jlu.edu.cn（Wang D H）.