分析化学中酸碱溶液pH计算的教学方法体会

钮树芳，杨 丹，薄彧坤，安 明

(包头医学院药学院，内蒙古 包头 014040)



分析化学中酸碱溶液pH计算的教学方法体会

钮树芳，杨 丹，薄彧坤，安 明

(包头医学院药学院，内蒙古 包头 014040)

分析化学是医药院校检验、药学、制药工程和生物技术等专业的一门专业基础课,溶液的pH计算公式多、运算推理复杂，学生难于理解和记忆；方法和结果：针对不同溶液的pH计算的内容共性和个性，通过归纳总结、类比、案例分析的教学方法，举一反三，突出重点，突破难点，激发了学生的学习兴趣；结论：在教学时数缩减而不减少教学内容的情况下，有效调动学生学习主动性，取得良好的教学效果。

分析化学；pH计算；教学方法；体会

分析化学是医药院校医学检验、卫生检验、药学、制药工程和生物技术等专业的一门专业基础课,是研究物质组成、含量、结构和形态等化学信息分析方法及理论的一门学科[1]。酸度是溶液中最基本和最重要的因素，因为许多化学反应都是在一定的酸度下进行的，而在酸碱滴定过程中，更需要了解溶液的pH变化情况[2]。因此，溶液中[H+]的计算具有重要的理论和实际意义。

“酸碱溶液[H+]的计算”这一节教学内容，一直以来，公式多、大量繁琐复杂的数学运算、严谨的逻辑推理，不便于学生理解和记忆[3]。尤其是随着我国高等学校教育课程体系改革的推进，分析化学的授课时数不断缩减[4]，因此，用较少的课时保证甚至提高教学质量，为学生后续的学习打下坚实的基础，笔者结合自已在分析化学教学工作的实践和经验，就如何突出重点和突破难点提出自已的一些见解和体会。

1 酸碱溶液[H+]计算的总体思路

酸碱反应的实质是质子的转移。当酸碱反应达到平衡时，酸所失去的质子数与碱得到的质子数相等。依据这一原则： ①列出溶液的质子条件式；②将酸的分析浓度ca和解离平衡常数Ka(或碱的分析浓度cb和解离平衡常数Kb)值代入质子条件式；③整理得出计算[H+]的精确式；④根据具体情况将精确式进行简化处理，可得近似式或最简式[5-6]。

2 各类溶液[H+]的计算

2.1 一元弱酸溶液[H+]的计算

以弱酸HA(浓度为camol·L-1，解离平衡常数Ka)为例，其溶液的质子条件式为：

[H+]=[A-]+[OH-]

溶液中的H+来自于两部分，即HA与H2O的离解。利用平衡常数将上式中各项写成[H+]的函数，则有

[H+]2=Ka[HA]+Kw

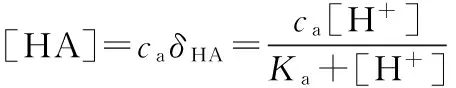
精确式：[H+]3+Ka[H+]2-(caKa+Kw)-KaKw=0

上式为计算一元弱酸H+浓度的精确公式。由于数学处理较麻烦，实际工作中也没有必要精确求解。因此，一般做如下近似处理：

(1)当Ka、ca均不太小时(caKa≥20Kw)，忽略水的离解(即忽略Kw)。

[H+]2≈Ka[HA]=Ka(ca-[H+])

整理后得：[H+]2+Ka[H+]-caKa=0

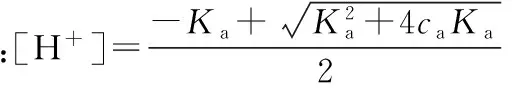
(2)当酸极弱，即caKa<20Kw，但浓度不是太小，即ca/Ka≥500，可忽略酸的解离，[HA]≈ca，溶液中的H+主要来源于H2O的离解，不能忽略H2O的解离。将[HA]≈ca代入式[H+]2=Ka[HA]+Kw中并整理得：

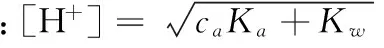
(3)当caKa≥20Kw，且ca/Ka≥500时，酸的解离和水的离解对总浓度的影响均可忽略。

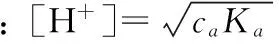
2.2 多元弱酸溶液[H+]的计算

以二元弱酸H2A(浓度为camol·L-1，解离平衡常数分别为Ka1、Ka2)为例，其溶液的质子条件式为：

[H+]=[HA-]+2[A2-]+[OH-]

将平衡常数和浓度代入质子条件式并整理得：

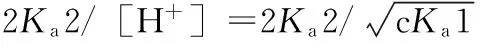
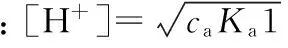
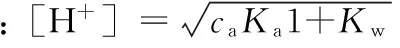
2.3 各类弱碱溶液[OH-]的计算

对于各类碱溶液中[OH-]的计算，与相应酸溶液的[H+]的计算相同，只需将上式中的[H+]、Ka和酸的浓度ca用[OH-]、Kb和碱的浓度cb代替。

如一元弱碱：

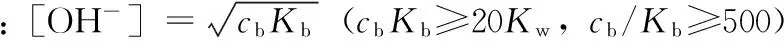
多元弱碱参照多元弱酸，在此不再赘述。

2.4 两性溶液[H+]的计算

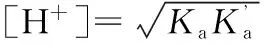
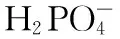
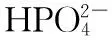
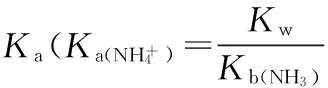
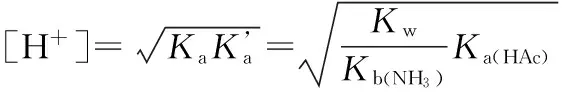
2.5 缓冲溶液[H+]的计算

缓冲溶液是一种能对溶液的酸度起稳定(缓冲)作用的溶液。假设缓冲溶液是由弱酸HA及其共轭碱NaA组成，它们的浓度分别为cHA和cA-。

溶液的质量平衡式：[HA]+[A-]=cHA+cA-

[Na+]=cA-

溶液的电荷平衡式：[Na+]+[H+]=[A-]+[OH-]

将[Na+]=cA-代入电荷平衡式，得：

[A-]=cA-+[H+]-[OH-]

将上式代入质量平衡式，得：[HA]=cHA-[H+]+[OH-]

由弱酸解离平衡常数得计算缓冲溶液H+浓度的精确计算式：

若溶液呈酸性(pH<6)时，可忽略[OH-]，得近似计算式：

若溶液呈碱性(pH>8)时，可忽略[H+]，得近似计算式：

若酸、碱分析浓度较大，即cHA≫[OH-]-[H+]，cA-≫[H+]-[OH-]时，得到计算缓冲溶液H+浓度的最简式

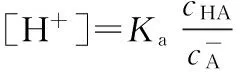
3 结论及案例解析

(1) 抓住只要记住一元弱酸这一具有典型性代表的基本公式，便能举一反三地记住一元弱碱和多元酸碱溶液pH计算公式，教学效果良好。

(2)计算各类酸(碱)水溶液pH：首先要判断是酸溶液还是碱溶液，若是酸溶液，要计算[H+]，若是碱溶液，要计算[OH-]，再计算pH；其次要用条件判别式判断，再选择相应的公式计算。

案例1：计算0.10 mol·L-1NH4Cl溶液的pH。

解析：NH4Cl为强酸弱碱盐，溶液显酸性， NH4+的Ka=5.7×10-10。

用条件式判断：caKa>20Kw，ca/Ka>500，可用最简式计算

pH=5.12

案例2：计算0.50 mol·L-1NaAc溶液的pH。

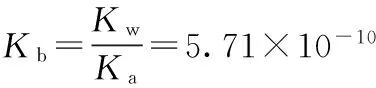
用条件式判断：cbKb>20Kw，cb/Kb>500，可用最简式计算：

pOH=4.77

pH=pKw-pOH=14.00-4.77=9.23

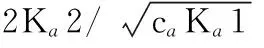
案例3：计算0.20 mol/L邻苯二甲酸溶液的pH。

解析：邻苯二甲酸Ka1=1.12×10-3，Ka2=23.90×10-6。

pH=1.83

(5) 缓冲溶液的缓冲容量与缓冲溶液的总浓度(cHA+cA-)和缓冲比(cA-/cHA)有关。缓冲溶液的总浓度越大，缓冲容量越大；缓冲溶液的缓冲比越接近1，缓冲容量越大。作为一般控制酸度的缓冲溶液，因缓冲剂本身的浓度较大，对计算结果也不要求十分准确，通常采用最简式进行计算。

[1] 李发美.分析化学.7版[M].北京:高等教育出版社,2011,8:1-2.

[2] 毋福海.分析化学.2版[M].北京:高等教育出版社,2015,1:89.

[3] 陈翠莲,孙莉娜.《分析化学》pH值计算的教学方法改革[J].漳州职业技术学院学报,2009,11(1):65-67.

[4] 孙静,李思,陈嘉曦. 对医学院校分析化学教学中存在问题的思考[J].广州化工,2016,44(5):187-188.

[5] 胡琴.分析化学(案例版).2版[M].北京:科学出版社,2016(6):45.

[6] 刘林.酸碱溶液的质子条件及其应用[J].阿坝师范高等专科学校学报,2015,32(3):124-126.

Experience of Teaching Method of pH Calculation in Acid-base Solution in Analytical Chemistry

NIUShu-fang,YANGDan,BOYu-kun,ANMing

(Department of Pharmacy, Baotou Medical College, Inner Mongolia Baotou 014040, China)

In laboratory medicine,pharmacy, pharmaceutical engineering and biotechnology professional，Analytical Chemistry is an important professional basic course. There are more formulas and complex mathematical operations of pH calculation in solution of Analytical Chemistry,which are difficult for students to understand and remember. According to the character and individuality of different solutions for pH calculation, the teaching methods of induction, analogy and example analysis were applied for students drawing inferences about other cases from one instance. It could give prominence to emphasis and overcome difficulties,to have stimulated students’ interest in learning. In the case of teaching hours reduced without reducing teaching content, the students’ learning linitiative were inspired effectively,and the better teaching effect was obtained.

analytical chemistry; pH calculation; teaching method; experience

钮树芳(1972-)，女，硕士，副教授，主要从事中蒙药化学及分析化学教学研究。

O651

A

1001-9677(2016)020-0189-03