一类具阻尼项的三阶半线性中立型泛函微分方程的Philos型振动结果

林文贤

(韩山师范学院 数学与统计学院，广东 潮州 521041)



一类具阻尼项的三阶半线性中立型泛函微分方程的Philos型振动结果

林文贤

(韩山师范学院 数学与统计学院，广东 潮州 521041)

论文研究一类具有阻尼项的3阶半线性中立型泛函微分方程的振动性质,利用广义Riccati变换、平均不等式技巧和H-函数技巧,建立了保证该类方程的一切解Philos型振动或者收敛于零的若干新的充分条件,推广和改进最近文献的相应结果.

3阶泛函微分方程；阻尼项；Philos型振动

由于3阶微分方程的实际应用背景，近年来，3阶泛函微分方程的振动性和渐近性研究开始受到关注，最近的成果可以参看文献[1-12].论文将考虑如下的一类具阻尼项的3阶半线性中立型泛函微分方程

(1)

其中:α是两个正奇整数之比.

记I=[t0,+),R+=(0,+)，假设下列条件成立

(H1)r(t)∈C(I,R+),p(t),m(t)∈C(I,[0,+)),r′(t)≥0，0≤p(t)≤P<1，且

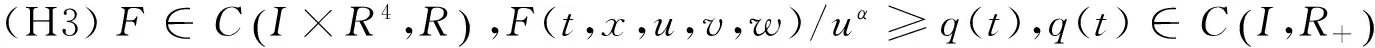
作者的目的是利用广义Riccati变换和H-函数技巧,建立使得方程(1)的每一个解Philos型振动或收敛于零的充分条件.当m(t)=0时,方程(1)就是文献[9]所研究的方程，因而论文的结论推广和包含文[9]的相应结果.

引理1[10]设 u(t)>0,u′(t)>0,u″(t)≤0,t≥t0，则对任一θ∈(0,1),存在Tα≥t0，使得

引理2[11]设u(t)>0,u′(t)>0,u″(t)>0,u‴(t)≤0,t≥Tα,存在β∈(0,1)和Tβ≥Tα,使得

引理3[12]设X,Y是非负常数，则Xγ+(λ-1)Yλ≥λXYλ-1，γ>1，当且仅当X=Y时等号成立.

引理4 设x(t)是方程(1)的最终正解,令

(2)

则y(t)只有下列两种可能，即存在T≥t0，使得当t≥T时，有

(A) y(t)>0,y′(t)>0,y″(t)>0.

(B) y(t)>0,y′(t)<0,y″(t)>0.

证明 设x(t)是方程(1)的最终正解及条件(H3),存在t1≥t0，当t≥t1时，有

易知y(t)>x(t)>0 ,且

则

在[t2,t)上对上式积分,有

为了证明下面的定理，引进如下一类函数F.令D0={(t,s)|t≥s≥t0},D={(t,s)|t>s≥t0}.称函数H(t,s)∈C1(D,R)称为属于F类,记作H∈F,如果

(i)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0;

(ii)H在D0上第二个变量有连续非正的偏导数.

定理1 设存在函数H∈F和h∈C(D0,R)，ρ∈C1(I,R+)，使得

(3)

(4)

(5)

其中

(6)

其中：θ,β由引理1、2定义,则方程(1)的每一解x(t)振动,或者当t→时，x(t)→0.

证明 设方程(1)存在非振动解x(t),不失一般性,设x(t)>0,t≥t1≥t0(对于x(t)<0的情况可用同样的方法证明),根据引理4,由(2)所定义的y(t)具有性质(A)或(B).

(i) 若y(t)具有性质(A)，则 y′(t)>0,有

(7)

故由(H3)得到

(8)

定义

(9)

则 W(t)>0,t≥t1，且利用(7)和(8)可得

(10)

在引理1中，令u(t)=y′(t)，有

(11)

利用引理2，得到

(12)

在(10)中利用(11)和(12)产生

其中：Q(t)由(6)定义.

(13)

令

在不等式(13)中应用引理3，得到

即

(14)

显然，(14)与条件(4)矛盾.

(15)

(16)

(16)可写成

(17)

注意到yα[g(t)]≥lα和 E′(t)≥0,有

对上式从t1到积分，有

上式与(5)矛盾.因此,l=0.

注 设若取H(t,s)=(t-s)n，则定理1成为方程(1)的Kamenev型振动准则.

[1] GRACE S R,AGARWAL R P,PAVANI R,et al.On the oscillation criteria for third order nonlinear functional differential equations[J].Appl Math Comput,2008 (202)：102-112.

[2] DZURINA J.Asymptotic properties of the third order delay differential equations[J].Nonlinear Anal TMA,1996 (26):33-43.

[3] TIRYAKI A,AKTAS M F.Oscillation criteria of a certain class of third order nonlinear deay differential equations with damping[J].J Math Anal Appl,2007 (32):54-68.

[4] 林文贤.一类非线性中立双曲型偏泛函微分方程的振动性[J].安徽大学学报 (自然科学版),2011,35 (3)：9-13.

[5] 林文贤.一类具分布时滞的中立型双曲方程的振动性[J].安徽大学学报 (自然科学版),2013,37 (6)：8-12.

[6] 林文贤,俞元洪.高阶中立型时滞微分方程的振动准则[J].应用数学学报,2014,37 (6):1018-1024.

[7] 林文贤.振动性和周期解理论的研究[M].北京：国防工业出版社，2014.

[8] 林文贤.三阶非线性中立型阻尼泛函微分方程的振动性[J].安徽大学学报 (自然科学版)，2015，39 (3):5-9.

[9] 罗李平,俞元洪.三阶半线性中立型微分方程的振动结果[J].系统科学与数学,2012,32 (5):571-579.

[10] ERBE L.Oscillation criteria for second order nonlinear delay equations[J].Canad Math Bull,1973 (16):49-56.

[12] HARDY G H,LITTLEWOOD J E,POLYA G.Inequalities[M].Cambridge:Cambridge University Press,1988.

(责任编辑 朱夜明)

Oscillation results of Philos-type for third-order half linear neutral damped differential equations

LIN Wenxian

(School of Mathematics and Statistics,Hanshan Normal University,Chaozhou 521041,China)

In this article,the oscillation of third-order half linear neutral damped functional differential equations was studied.By using the generalized Riccati transformation,the averaging inequality technique and H-function technique,some new sufficient conditions which insure that any solution to such equation oscillates or converges to zero was established.The corresponding results in known literature was extended and improved.

third-order functional differential equations;damping terms ;Philos-type oscillation

10.3969/j.issn.1000-2162.2016.06.001

2015-01-16

广东省高等教育教学改革项目(GDJG20142396);广东省高等学校特色创新项目(2014GXJK125)

林文贤(1966- )，男，广东潮州人，韩山师范学院教授.

O175

A

1000-2162(2016)06-0001-04