基于PCA-SVR的池塘DO预测模型

吴慧英，杨日剑，张 颖，蒙语桦

(湖南大学 土木工程学院，湖南 长沙 410000)



基于PCA-SVR的池塘DO预测模型

吴慧英，杨日剑，张 颖，蒙语桦

(湖南大学 土木工程学院，湖南 长沙 410000)

为解决传统水质预测模型泛化能力低、预测精度差等问题，提出了基于主成分分析和支持向量机相结合的养殖池塘溶解氧预测模型.该模型通过主成分分析筛选反映池塘水体溶解氧信息的关键指标，减少模型输入变量，采用支持向量机算法建立水质预测模型，并用于长沙市乔口镇与望城区池塘养殖溶解氧预测中.结果表明,该模型预测精度高，同时具有很强的泛化能力与适应数据变化的能力，可用于池塘溶解氧预测.

主成分分析；支持向量机；水质预测；养殖池塘

溶解氧浓度是养殖区域水环境规划和现代渔业健康养殖精准化管理的重要基础性工作，准确的溶解氧预测对养殖水质科学化调控、防范水质恶化和控制水产品疾病爆发具有十分重要的经济价值和现实意义[1].目前常用的水质预测方法有指数平滑法[2]、专家评估法[3]、多元回归法[4]、灰色模型法[5-6]等.然而这些方法只适用于样本数量较大、维数较低和线性程度较高的水质预测，对于非线性、高维数和小样本水质数据预测效果不佳.神经网络法具有较好的非线性预测能力，但也容易出现局部极值、过学习等问题[7-8].支持向量机是基于VC维和结构风险最小原理的一种新型机器学习方法，不仅适用于非线性问题，还能够克服传统智能算法出现的过学习、小样本时泛化能力差等多方面的缺点[9].

池塘养殖中溶解氧浓度预测需要多种水质指标作为输入变量，但变量过多，会造成一定的信息重叠，同时造成计算复杂，易陷入局部优化问题，使预测结果准确性下降.针对这些问题，笔者提出采用主成分分析与支持向量机相结合的方法进行养殖水质预测，主成分分析法能够从众多水质指标中筛选出能够反映水质主要情况的关键性指标，剔除伪指标，然后将选取的主要水质指标作为输入样本建立支持向量机水质预测模型，并以养殖水体为例进行水质预测，该方法收敛速度快，预测精度较高.

1 基本原理

1.1 主成分分析法

由于影响养殖池塘水质的评价指标较多，且每个指标都能在一定程度上反应水体的部分信息，同时指标之间也存在相关或重叠的关系，这样就导致在用多元统计方法进行多变量问题求解时，增加问题的复杂性及求解的计算量，还有可能导致问题求解精度下降.在实践中人们希望尽可能地减少变量的个数，用更少的变量反映尽可能多的信息，而主成分分析方法(principal component analysis，简称PCA)正是一种将多维因子纳入同一系统进行定量化研究且理论比较完善的多元统计分析方法，在解决很多实际问题时已取得较好效果[10].

主成分分析法的基本思想是指采用降低维数的方法，在失去很少信息的前提下，将各种原始变量转化为几个指标(称之为主成分)之间的线性组合，剩下的信息称之为原始变量[11].这样在数据指标较多的水质评价研究中，就可以把复杂的多维问题转化成低维问题且最大程度地保留原始数据信息.主成分分析法的主要步骤为：

(1) 数据标准化.设有n个样本，每个样本有m项指标，对样本进行标准化为

(1)

其中：zij为标准化后的指标值,xj是第j项指标数据的平均值,sj是第j项指标数据的标准差.

(2) 计算相关矩阵.对标准化的数据进行相关分析，计算相关矩阵R

(2)

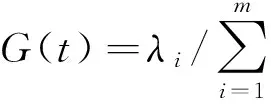
(4) 计算主成分y

(3)

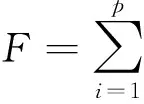
1.2 支持向量机预测方法

支持向量机是建立在统计学习理论的VC维理论和结构风险最小化原理基础上的一种新的机器学习算法[10,12-15].该算法根据有限的样本信息采用非线性映射Φ把数据映射到一个高维特征空间中去，使得样本在高维空间中进行线性回归.由泛函模型可知，只要存在一种满足Mercer条件的函数K(xi,xj)，K(xi,xj)=Φ(xi)×Φ(xj)，就与某一空间中的内积相对应，这样监测数据在高维空间内积可转换为核函数内积，使计算工作量大大减少.因此该非线性函数可构造为

(4)

由式(4)可知，无需知道非线性映射Φ，而只要找到一个核函数，就可以通过该核函数进行非线性处理，对于函数的回归问题，其估计函数就是核函数的线性组合.

1.3 养殖池塘组合预测模型的建立

基于主成分分析的支持向量机池塘养殖溶解氧组合预测模型原理是将参加水质预测的水质指标进行主成分分析，筛选出影响池塘养殖溶解氧浓度的关键指标作为支持向量机的输入向量，降低预测维数，然后通过预测样本训练此模型，使不同的输入向量得到相应的输出值，从而建立一种水质预测结果与实际值的非线性映射关系，经过学习达到一定精度后，该非线性预测模型可成为养殖水体水质组合预测的有效工具.具体步骤为：

(1) 选择影响池塘溶解氧浓度关键指标.由于影响养殖水体溶解氧浓度的因素较多，关系较为复杂，对初始水质指标进行主成分分析，筛选出养殖水体溶解氧关键指标.

(2) 数据归一化.以主成分分析筛选的关键指标作为预测模型输入变量，采用最大-最小值法对变量进行归一化处理，消除指标量纲之间影响.

(3) 建立支持向量机预测模型.选择合适的SVR核函数和模型参数，通过对训练样本进行训练构造预测模型，并分析拟合误差，当模型精度达到预定要求时就完成相应的预测建模.以测试样本对模型进行检验，验证其泛化性能.

2 实例应用

2.1 研究区域及监测指标的选取

乔口镇地理位置独特，四面环水(湘江、柳林江、撇洪河、团头湖)，养殖水面广阔，除面积为8 000多亩的团头湖外，另有青草湖、南湖、湛湖等大小湖泊池塘近20 000亩，是望城区“百里水产走廊”的核心区，因此，准确预测乔口镇池塘养殖水质为当地生产与管理提供可靠依据，具有重要意义.

影响池塘溶解氧因素众多，十分复杂，主要包括气压、温度、光强、人工增压、池塘中氧气的消耗等，但上述影响因素在一定条件下具体到某一池塘监测断面时可认为是不变的[16]，而该课题在以国家“十二五”科技支撑项目“村镇环境监测与应用示范”基础上，综合考虑各指标在线监测可能性的情况下，选择总磷、总氮、氨氮、硝酸盐、亚硝酸盐、化学需要量、温度、SS、电导率等指标作为输入变量进行分析，溶解氧为输出变量.

2.2 池塘养殖水质关键指标筛选

为消除数据间的多重共线性，提高预测速度，采用主成分分析法对养殖水质进行分析，筛选影响溶解氧值的关键指标.按照主成分分析法的步骤采用MATLAB软件对养殖水体水质指标进行筛选，因水质数据间的非线性较强，采用正态标准化方式进行数据预处理，以此标准化数据为基础得到主成分特征值与贡献率，如表1所示.

表1 特征值与累计方差贡献率

由表1可知，前3个成分的累计方差贡献率达到88.76%，符合累计方差贡献率大于等于 85% 作为提取主成分的原则，因此，可确定前3个因子代替原变量.

根据特征值及特征向量，计算各水质指标的主成分荷载，计算结果如表 2所示.

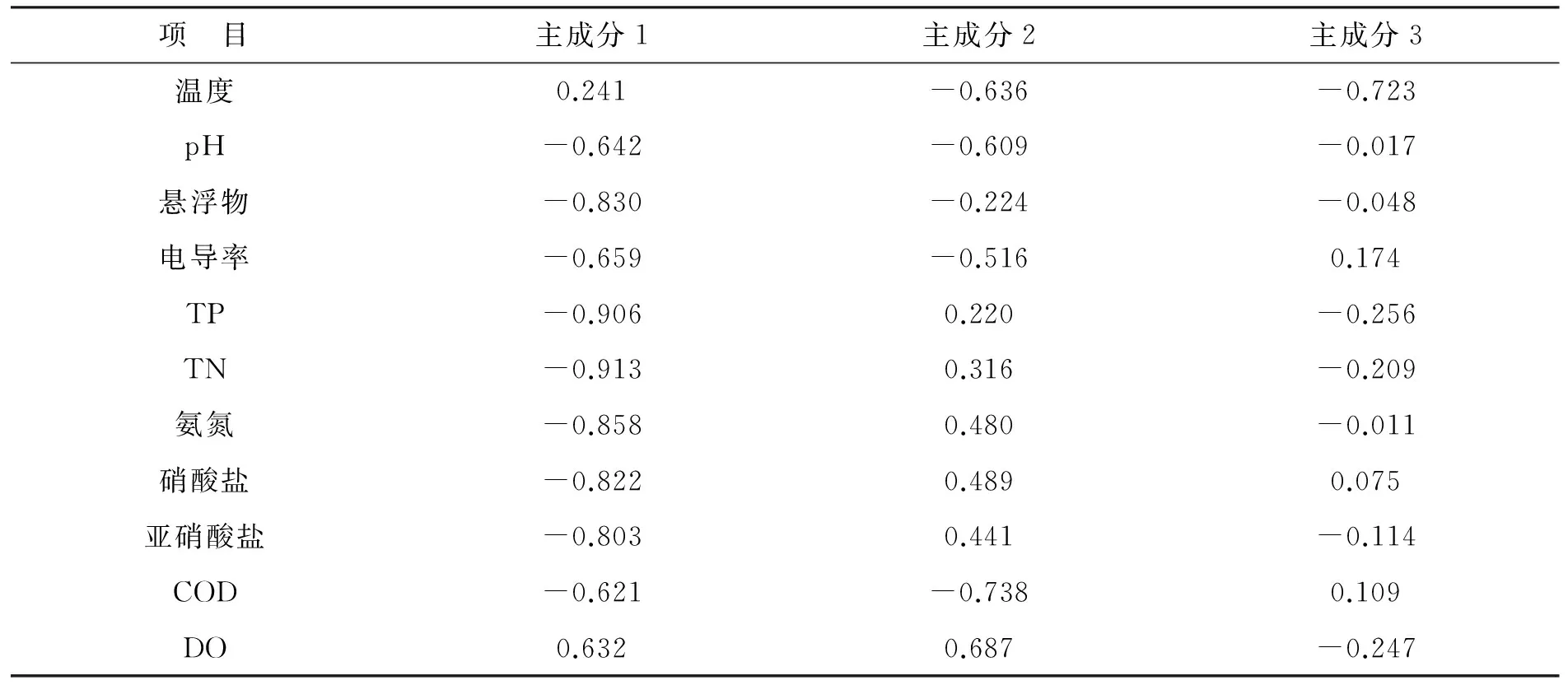
表2 主成分载荷矩阵

从表2可知，第1主成分中总磷和总氮的相关系数较高，绝对值超过了0.9，第2主成分中化学需氧量与溶解氧相关系数较其他水质指标高，绝对值超过0.65，第3主成分中起主要影响的为温度，其相关系数绝对值为0.723.结合水体实际情况，笔者选用总氮、总磷、化学需氧量和温度作为影响水质溶解氧的关键指标，并以此为构建支持向量机预测型的输入样本.

2.3 支持向量机预测模型

根据主成分分析法选择的影响养殖水质关键指标，以养殖水体最不利断面连续15 d(2015年1月18日至2月1日)共30组的监测数据为基础，并将数据分割成两部分.以1月18日至1月28日数据为训练样本，建立预测模型；以1月29日至2月1日为测试样本，验证所建模型的准确性及推广能力，并与传统的SVR模型和BP神经网络模型进行比较，验证模型的优越性.各方法的预测结果见表3.

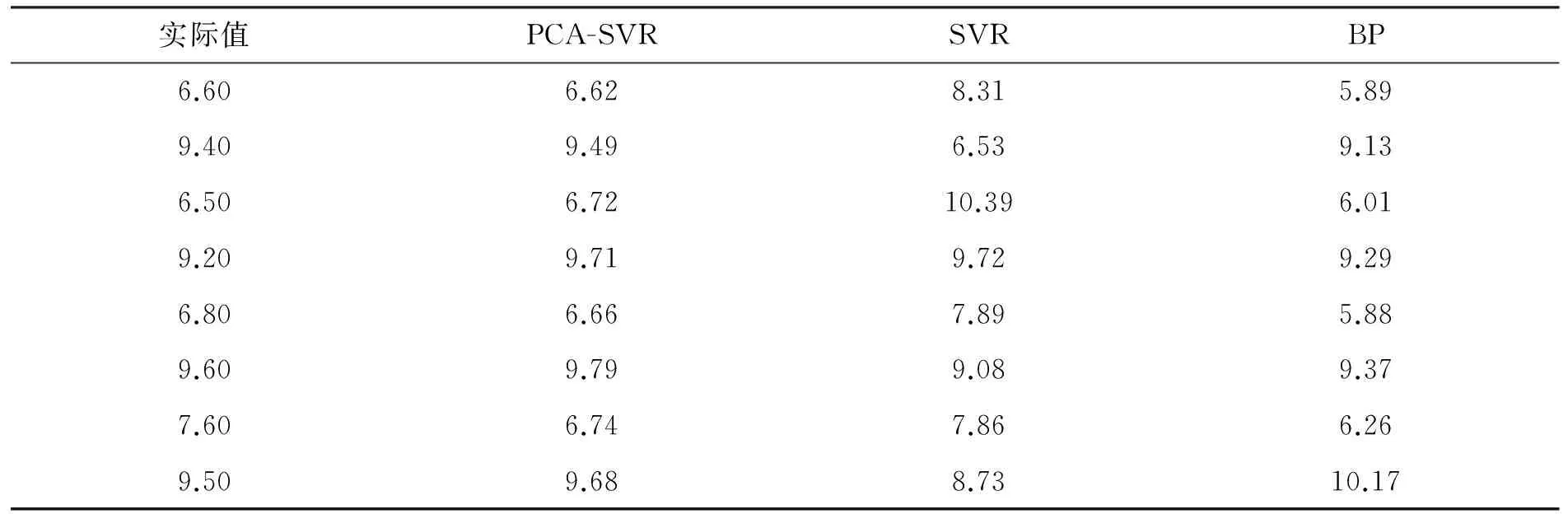
表3 溶解氧预测结果

由表3可知，在训练样本较小时，PCA-SVR模型预测值较SVR模型和人工神经网络模型更接近实际值，预测效果更好.

为进一步分析对比PCA-SVR、SVR和BP神经网络三种预测模型效果，必须选择一套客观科学的评价指标对预测效果进行全方位的综合性衡量和评价，使得预测效果更加直接，更加可靠.按照预测效果评价原则和惯例，采用均方误差(MSE)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE)作为评价指标，评价结果见表4.

表4 三种模型误差对比

由表4可知，BP神经网络模型的均方误差、平均绝对百分比误差和均方百分比误差分别为9.58%，7.85%和24.18%，SVR模型的均方误差、平均绝对百分比误差和均方百分比误差分别为2.40%，19.39%，35.18%，而PCA-SVR模型的均方误差、平均绝对百分比误差和均方百分比误差最小，分别为4.78%，3.43%，10.86%，说明无论是相对误差、平均绝对百分比误差还是均方百分比误差PCA-SVR模型都比SVR模型和BP神经网络模型精度高，主要原因是人工神经网络模型只是建立局部优化的基础上，容易造成局部极值，使训练失败，传统的SVR模型由于指标数多，维数大，干扰大，造成信息过度重叠，预测精度降低，而PCA-SVR模型通过主成分分析保留了影响溶解氧浓度的关键信息，同时剔除了增加运算时间和干扰预测性能的噪声数据，因此预测精度高，泛化能力强.

2.4 预测应用

将预测模型应用到长沙市某池塘养殖水体中，预测水体中溶解氧未来变化趋势，以进一步验证该模型的普适性和精确性，步骤与上述类似，首先进行主成分分析，选择影响溶解氧的关键指标作为输入变量，考虑数据的可在线监测性，主要选择pH、BOD、COD、总磷、总氮、氨氮、硝态氮、亚硝态氮、溶解氧等指标进行分析，主成分分析结果列于表5.

表5 溶解氧影响系数

从表5可知，第1主成分中BOD5和COD的相关系数较高，绝对值超过了0.3；第2主成分中总磷与氨氮相关系数较其他水质指标高，绝对值超过0.1.因此结合水体实际情况，选用BOD5、COD、总磷和氨氮作为预测型的输入样本.

根据主成分分析法选择的输入变量，以该水体最不利断面连续15 d的30组监测数据为基础，以前11 d的22组数据为训练样本，建立预测模型；对最后4 d的8组数据进行预测对比，进一步验证所建模型的准确性和适用性，预测结果列于表6.

由表6可知，PCA-SVR模型预测值与实际值接近，预测精度较高，最大相对误差仅为13.49%，而绝大部分误差精度在10%以内，满足实际应用需求.因此，基于PCA-SVR的溶解氧预测模型能够较准确地预测池塘养殖水体溶解氧数据变化情况，具有使用价值.

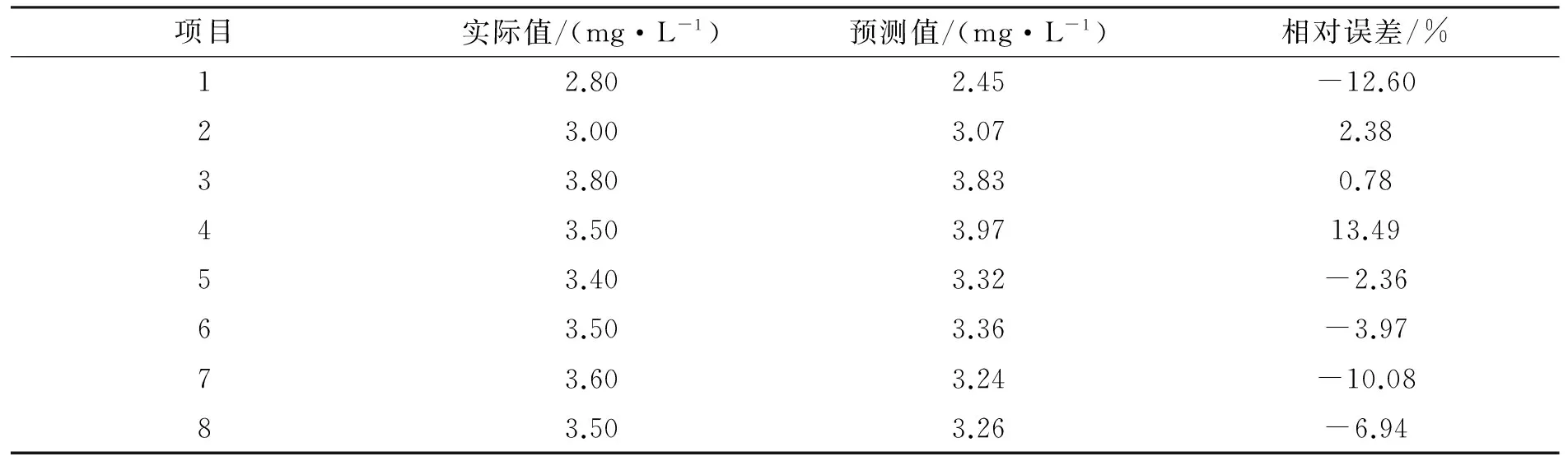
表6 预测结果对比

3 结束语

作者将主成分分析与支持向量机结合进行养殖水质预测，主成分分析提取影响养殖水体溶解氧浓度的关键指标，可以降低模型输入变量维数，提高模型的训练速度，从而提高水质预测的实时性，而支持向量机预测模型具有预测精度高，泛化能力强，抗噪性能强等优点.通过与传统SVR模型和BP神经网络模型预测结果的对比分析可以看出，笔者文中提出的PCA-SVR预测方法得到令人满意的结果，是预测水质较理想方法，可以用于实际生产.

[1] 刘双印,徐龙琴,李振波,等.基于PCA-MCAFA-LSSVM的养殖水质pH值预测模型[J].农业机械学报,2014,45 (5):239-246.

[2] 李燕斌,张久菊,肖俊明.基于指数平滑法的灰色预测模型[J].中原工学院学报,2015,26 (4):1-4.

[3] 李昌铸,王丽云.特尔斐专家评估法在公路桥梁评价中的应用[J].中国公路学报,1993，6 (2):47-53.

[4] 汤志成,孙涵.最优化因子处理及加权多重回归模型[J].气象学报,1992，50 (4):514-517.

[5] 张秀芝,王静,张雨山,等.基于GM(1,1)灰色模型预测沿海城市用水量——以大连市为例[J].海洋技术学报,2014，33 (2):47-51.

[6] DELLANA S,WEST D.Predictive modeling for wastewater application:linear approaches[J].Environmental Modeling and Software,2009,24 (1):96-106.

[7] ÖMER FARUK D.A hybrid neural network and ARIMA model for water quality time series prediction[J].Engineering Applications of Artificial Intelligence,2010,23 (4):586-594.

[8] PALANI S,LIONG S Y,TKALICH P.An efficient self-organizing RBF neural network memory structures for basin water quality forecasting[J].International Journal of Forecasting,2011,27 (3):777-803.

[9] 李黎武,施周.基于小波支持向量机的城市用水量非线性组合预测[J].中国给水排水,2010,26 (1):54-57.

[10] 库路巴依,白云鹏,王玲.主成分分析法在水库水质综合评价中的应用[EB/OL].北京:中国科技论文在线 [2008-02-28].http://www.paper.edu.cn/releasepaper/content/200802-357.

[11] ZHANG X,WU J,SONG B.Application of principal component analysis in groundwater quality assessment [C]// Water Resource and Environmental Protection (ISWREP),2011 International Symposium on IEEE,2011:177-183.

[12] 宋来洲,白明华,李健.微滤分离膜在城市污水深度处理中的应用[J].安全与环境学报,2004,4 (5):12-15.

[13] 王红瑞,刘晓红,唐奇,等.基于小波变换的支持向量机水文过程预测[J].清华大学学报 (自然科学版),2010，50 (9):1378-1382.

[14] 张土乔,俞亭超.提高支持向量机洪水峰值预报精度研究[J].水力发电学报,2005,24 (2):35-39.

[15] 刘双印,徐龙琴,李道亮,等.基于时间相似数据的支持向量机水质溶解氧在线预测[J].农业工程学报,2014，30 (3):155-162.

[16] 郭连喜,邓长辉.基于模糊神经网络的池塘溶解氧预测模型[J].水产学报,2006,30 (2):225-229.

(责任编辑 于 敏)

Forecasting model for DO of pond water quality based on PCA-SVR

WU Huiying，YANG Rijian，ZHANG Ying，MENG Yuhua

(College of Civil Engineering College,Hunan University,Changsha 410000,China)

In order to solve the problem of low prediction accuracy and poor generalization ability of the traditional forecasting methods in water quality,this paper proposed forecasting model for DO value of pond water quality based on PCA-SVR.The model picks key indicators which can reflect DO condition of pond water environment by the principal component analysis,reduce the model input variables,uses support vector machine algorithm for establishing water quality prediction model and adapts it to pond aquaculture water of Qiaokou town and Wang cheng district,Changsha.The application examples show that the model prediction has strong generalization ability and adaptability to change of data and functions，meanwhile has high prediction precision,it can be used to forecast aquaculture water dissolved oxygen quality.

principal component analysis;support vector machine;water quality forecast;pond aquaculture water

10.3969/j.issn.1000-2162.2016.06.017

2015-08-28

“十二五”国家科技支撑项目(2012BAJ24B03)

吴慧英(1967-)，女，湖南长沙人，湖南大学副教授，研究生导师.

TV213

A

1000-2162(2016)06-0103-06