端面锥形参数对锥-孔组合型机械密封性能的影响

程香平，孟祥铠，彭旭东，张友亮，付远，康林萍



端面锥形参数对锥-孔组合型机械密封性能的影响

程香平1，孟祥铠2，彭旭东2，张友亮1，付远1，康林萍1

（1江西省科学院应用物理研究所，江西南昌330029；2浙江工业大学过程装备及其再制造教育部工程研究中心，浙江杭州 310032）

给出新型锥-孔组合型端面密封，考虑液膜压场的变化规律与环受力变形的相互作用关系，构建机械密封3D流、固耦合数学模型，并给出相关的数值计算方法，获得了膜压分布规律及端面变形情况，分析锥面结构参数在各工况下对密封性能的影响规律。结果表明：由菱形孔所引起的动压效应可使端面产生周向和径向波状变形，而静压效应随锥度和锥宽比的变化，在端面区域范围内所起作用也发生相应变化；对压强较低和低、中转速设备，应选取=5～6或=2～4的收敛锥面密封，且=0.8～1.0。对高压和高速设备，应选用=2～3的收敛锥面密封，且=1.0或=0.2；通过改变锥面结构可有效改变机械密封的特性参数，实现密封运行中的自动调节，特别适合变工况条件。另外，由于锥面结构的变化所引起平衡系数和膜厚的变化，低速时可弥补动压效应较小的缺陷，获得较大开启力，也可在大下工作，故可降低密封端面对平整度和光洁度的要求。

数值模拟；流体动力学；端面变形；层流

引 言

20世纪80年代初Etsion[1]初步研究了锥面密封的性能参数，并阐述了锥面密封的可行性。Lebeck[2]指出，端面液膜沿介质泄漏方向呈收敛楔形时，可提供足够大的轴向承载能力。Zheng等[3-4]研发出一种自加压双螺旋槽动静压混合式机械密封，并得到了极好的试验验证。但在实际应用中由于安装、端面磨损及热力变形所形成的径向锥度难以控制，极易造成泄漏超标和端面失衡，且也难以形成较好的开启性能[5-8]，故在工程中较少应用。但随着LST-MS技术的发展，激光加工微孔端面密封显示出极好的动压性能[9-11]，彭旭东等[12]结合锥面机械密封和LST-MS各自明显特性，提出锥面-微孔端面组合密封新技术，在一定工况范围内有较好的适应性，并取得很好的实验效果和实践应用。

鉴于此，作者综合考虑机械密封运行过程中多变工况所引起的各种不利因素，例如启-停、振动、变速和变压等对密封装置中的介质汽化、环变形和端面磨损等现象[13-15]，系统研究了大孔径端面织构和锥-大孔端面的机械密封的各种孔型参数对密封性能的影响情况，得出较大菱形孔织构端面具有比微孔织构更好的密封性能和变工况自适应性[16-19]，故本文着重研究锥面几何参数对锥-孔组合型机械密封性能的影响规律，并综合考虑密封装置轴向力的动态平衡和端面变形，构建端面间膜压和密封环受力变形控制理论模型，在多变工况条件下对机械密封的三维流、固耦合理论模型进行离散求解，并对计算出的液膜压场变化规律和密封环受力变形情况进行动态分析，进而得出密封性能参数和结构设计参数，以期提出变形协调和控制的方法，进一步完善动静压组合型机械密封的设计理论。

1 模 型

1.1 几何模型

图1给出锥-菱形孔端面组合型机械密封的局部结构示意图。静圆环端面加工成一定锥度的斜面，且定义锥度=100(o-m)tan/0[12]，其中为锥面锥角，m为锥面起始半径，i、o分别为密封端面内、外半径，0为端面液膜的基础膜厚。“锥宽比”是非锥面半径与端面外径比值，即=m/o；动圆环上的菱形孔沿密封端面周向呈对称分布、径向呈等距分布，菱形孔为等深孔，其深度为1。采用两个结构参数和来表示菱形孔的几何特征，定义长短轴比＝/，其中为菱形孔对称轴的半长轴，为半短轴。

因所建力学模型具有中心对称性，少占用计算机内存，故只需建立单周期几何模型，图2是有限元模型边界条件示意图。密封环A和B曲面分别与相对应面构成周期性边界条件，如图2(a)所示。静圆环采用固定约束，动圆环采用指定位移，同时受弹簧力sp和外压o的作用，密封端面施加力为计算的端面膜压，如图2(b)所示。另外，由于在运转中孔区和非孔区液膜厚度均极小，端面间压强在液膜厚度方向上的压差变化无论在孔区或非孔区均可忽略不计，所以密封端面的整体变形量不会因菱形孔的存在而产生较大变化，故在计算变形时可忽略菱形孔的影响，仅在计算分布时需考虑菱形孔的存在。

1.2 理论模型

假定端面间流体压力沿膜厚方向恒定不变；密封介质为牛顿型流体，其黏度保持不变，考虑液膜空化作用，采用满足质量守恒的圆柱坐标系形式Reynolds方程[20]

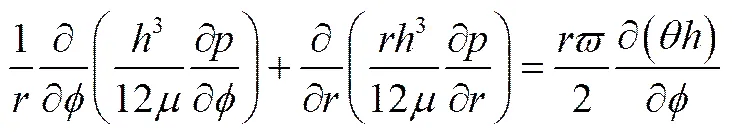
式中，为液膜密度与未空化液体密度之比，即：=/，在非空化区为=1，>cav，而在空化区0<<1，=cav；为液膜厚度，为介质黏度；cav为液膜空化压力；平均转速，其中为旋转环转速。

膜厚方程

式中，h为动圆环面上某点的变形量；h为静圆环面上某点变形量；h为锥面上某点锥高。

当密封装置稳定运行时，密封环轴向受力平衡，则

c=o(3)

其中，

(5)

式中，c为闭合力，o为开启力，sp为弹簧比压，为平衡系数，i和o分别为端面内、外径处压力。

采用有限差分法将式(1)进行离散，再与式(2)～式(5)进行联合求解，构建流体动静组合型机械密封三维流、固耦合数学模型，利用Matlab编程计算，用有限元软件计算三维模型的固体变形量，以变形后再次求解分布，反复迭代直至满足收敛判据即停止，用最终值求解液膜刚度z、o和泄漏率等性能参数，具体算法详见文献[16-17]。

2 计算结果与讨论

几何参数：o=143 mm，i=129 mm；=2 mm，1=1.5 μm，单列孔个数s=4，=1.67，动、静密封环弹性模量分别为1617GPa和223GPa，动、静密封环厚度分别为b1=8 mm和b2=10 mm，动、静密封环泊松比分别为1=0.28和2=0.25，=4，=1，=0.82，sp=0.15，=150。

工况参数：i=0.1 MPa，低压o=0.3 MPa，高压o=6.6 MPa，=0.001 Pa·s，=1500 r·min-1。

规定端面变形位移量以动、静圆环的轴中心线为直角坐标轴轴，各自原密封端面处为0基准点，轴正向为负值，负向为正值。在计算分析和研究某参数和工况条件对变形及密封性能参数影响时，除说明外，其他几何参数和工况参数均保持不变。

2.1对端面力变形的影响

图3示出了o=1 MPa和变化时密封端面变形及液膜压场的情况。由图可知：因为端面菱形孔的存在能够产生很强的动压效应，致使端面间膜压产生非常规则的高、低压(孔区某些区域会出现空化现象，即膜压图所示孔内最小压力平底区)相间的周期性波状分布态势，最高压力峰值高随的变化而变化，且高(Ф=0)高(Ф=2.4)高(Ф=4)，故而端面间压差∆(Ф=0)变化幅度最大，∆(Ф=2.4)和∆(Ф=4)依次减小。另外，变化时其高、低压区域范围的大小也是不同的，=0的低压区范围很大，高压区范围很小，因此这种流压场状况极易造成密封端面运行的不稳定；相比之下，=2.4的膜压场高、低压区域范围的大小较均衡，压差变化也不大，因此该种状态下的密封面在运行中会非常平稳，难以接触，不易磨损，而=4的端面密封的液膜稳定性居中。还可看出，高压区随着的增大由外径处逐渐向内径处增大，说明流体静压效应作用的范围随的增加沿径向由外径到内径处增大，而动压效应则随之减弱。低压波谷区位于孔内与转速同向一侧，存在着空化区域，这说明流体在孔区受边界阻滞一侧产生高压，另一侧因流体背离而产生空化现象。

综上所述，在流体动压和静压效应的共同作用下，端面间膜压场形成有规律的波动压力区，致使密封环面受到压缩形成凸凹不平的变形曲面，且变形情况与膜压场的形状有关，膜压较大区域对应的端面区产生较大变形，压力较小区域产生的变形较小。由图3可看出密封端面变形的共性规律：在周向方向上形成具有中间凹陷的周期性波度曲面，且动、静圆环面上的变形方向相反；径向方向上也出现了有规律的径向波状起伏变形，中间变形幅度较大的，随后逐渐减小至内径侧。同时，不同值又具有各自的个性变形规律：随着的增加，端面最大和最小的变形量逐渐变小，由外径至内径处产生了发散状的变形锥度，这是由于随的增大，静压效应变强，动压效应变弱，使液膜在径向方向上形成收敛状膜厚，端面间的膜压整体变弱的同时，形成发散状液膜压场，故而产生了发散状的变形锥度。由图3(a)可知，=0时，中间的变形波幅值大于内外径处综合变形量，动、静圆环的最大变形量分别为0.01752mm和-0.4746mm(数值前的正负只代表变形的方向性)，最小变形量出现在谷底位置分别为0.01001mm和-0.1665mm；由图3(b)可知，在=2.4时，动、静圆环端面整体变形由外径处向内径处逐渐地增大，但最大变形量均出现在中间靠近内径处，分别为0.01608mm和-0.4196mm，由于密封端面存在一定的收敛锥度，使膜厚增大，故而静压效应作用范围变大，动压效应略微减弱，使端面变形存在轻微发散性。由图3(c)知，在=4时，动、静圆环面变形量由外径向内径处逐渐增加，再减小，最大变形量靠近内径侧，分别为0.01598mm和-0.4085mm，使密封端面径向锥度变形明显，径向波状变形有所减弱，而因动压效应产生的周向波状变形在靠近内径侧明显，外径侧减弱。

图4示出了o=1 MPa时，不同对密封性能参数的影响规律。结果表明：当=0、2.4和4时，由于轴向力的平衡作用，故而o的大小相差不大，但z(Ф=2.4)z(Ф=4)z(Ф=0)，这表明密封端面的液膜稳定性受到液膜压强波动均匀性和整体强度的影响较大，端面膜压越均衡，强度越大，液膜稳定性越好，z就越大，两端面在运行过程中就越平稳，越难以接触，工作寿命则变长。由图还可看出，min(Ф=2.4)min(Ф=4)min(Ф=0)和(Ф=4)(Ф=2.4)(Ф=0)，即min决定的大小。同时min越大，运行中的密封端面就越不易接触，难以磨损，但密封可靠性会变差；反之，min小，端面易接触，但变小，密封可靠性就变好。综上所述，考虑到液膜稳定性和密封可靠性，对中等压强和转速的设备，应选用=2.4收敛端面密封。

2.2 低压(0.3 MPa)工况时密封性能

2.2.1 不同时对密封性能的影响 图5示出了低压(0.3 MPa)工况和变化时对密封性能参数的影响。结果表明：随着的不断增大，和min均增加，而z(ω=800 r·min-1)z(ω=1500 r·min-1)z(ω=2500 r·min-1)z(ω=200 r·min-1)。这是因转速的增大，液膜动压效应增强，整个端面的高、低压区域范围的大小因转速越大越不均衡，所以z会逐渐减小。但z(ω=200 r·min-1)最小是因为在极低转速下产生很弱动压和静压效应共同作用的结果。同时，还可看出在极低转速(200 r·min-1)时，随的增大，z先缓慢减小后逐渐增大，并存在极小值，这是因为转速较低，端面间液膜的动压效应虽然较弱，但也起到一定的支撑作用，随着的增加，端面整体膜厚增大，动压效应变得更弱，在静压效应没发挥更强作用前，z就会减小。随进一步增大，极低的转速难以使膜厚变得更大，而内、外压差Δ所起作用的范围逐渐增大，静压效应的作用范围增大，故而端面的液膜稳定性逐渐变强，z变大；在转速≥800 r·min-1时，随的增大，z缓慢减小，原因在于：较高的转速会使端面间液膜的动压效应变强，随的增大，会引起端面间整体膜厚变大，动压效应会随之变弱，z就逐渐变小。由图5(b)可知，在低速(≤1500 r·min-1)时，随着的增加，和min均先缓慢减小后逐渐增大，当=2500 r·min-1时，和min是逐渐减小的。

综上所述，对于经常启停或转速较低的设备，应选=5～6的收敛端面密封。对于较高转速的设备，应选取=2～4的收敛密封端面。

2.2.2 不同时对密封性能的影响 图6示出了低压(0.3 MPa)工况和不同时，对密封性能参数的影响规律。结果表明：随的增大，动压效应逐渐增强，为保证o与c的平衡，min自动地增大调整，随之增大；而z基本上是随的增大而逐渐减小，但只有当0.4≤≤0.6时，z(ω=200 r·min-1)是最小的。还可看出，随着的增大，z先逐渐减小后快速增大，且存在极小值，而min和随着的增大，呈现出增—减—增—减的类似波浪状的曲线。其原因在于，初期随着的增大，静压效应所起作用的范围增大，引起整体及其收敛锥度变大，动压效应减弱，z逐渐减小。随的进一步增大，端面圆环宽度越来越小，端面间液膜受到微干扰范围变小，动压效应在较窄端面上所起液膜波动作用的差别变小，故液膜稳定性增强，z逐渐变大。因此，对于低压或速度较低的设备，为保持高的z和较好的密封性，应选取=0.8～1.0收敛端面密封。

我院2016年5月--2017年9月收治的64例行口腔修复患者,按照随机数字表法分为实验组和对照组,每组患者32例。实验组:男16例,女16例,年龄42-76岁,平均年龄(58.5±14.5)岁,病程1-5周,平均病程(2.5±0.5)周;对照组:男17例,女15例,年龄43-78岁,平均年龄(60.5±15.5)岁,病程1.5-5周,平均病程(3.25±0.75)周。将两组患者基本资料进行精细对比分析,差异不明显(P>0.05),具有临床可比性。所有患者均自愿入组并签署知情同意书。

2.3 高压(6.6 MPa)工况时密封性能

2.3.1 不同时对密封性能的影响 图7示出了高压(6.6 MPa)工况和变化时，对密封性能参数的影响规律，结果表明：在高转速时，随的增大，min和均逐渐增加，使端面间的摩擦磨损越来越弱，密封寿命增长，但密封性变差。而z随的增加基本上是先迅速增大而后逐渐减小，并在2≤≤3之间取得极大值，液膜稳定性最好，这是因为此时在动、静压效应共同作用下，使得端面间液膜的高、低压区域分布均衡且最大压差较小，故液膜最稳定。还可看出，在相同值条件下，越大，min和越大，而z在<2是变大的，在>2是减小的。原因在于：当<2时，整体的收敛性较小，也较小，在高速下整个端面的动压效应远大于静压效应，且整体较均衡，故z就会越来越大；当>2时，整体的收敛性随的增大将变得越来越大，而锥形膜厚会自动加大削弱外径侧液膜的动压效应，反之内径侧的动压效应加强，同时静压效应所起作用范围加大，在二者共同作用下，z随增大而逐渐减小。综上所述，对于高压和高速运转的机械密封设备，应选用收敛锥度=2～3的密封端面。

2.3.2 不同时对密封性能的影响 图8示出了高压(6.6 MPa)和不同时，对密封性能参数的影响规律。结果表明：随的增大，min和是逐渐增大的，而z呈现出增—减—增的变化趋势，整体图形呈躺着的“S”形，有极大值和极小值，且z在=0.2和1.0有极大值。还可看出，在相同下，随逐渐变大，z、min和均是增大的。这表明在高压时，随增大，动压效应逐渐增大，从而抵消了内外静压差所产生静压效应的不均衡，使端面液膜更稳定。综上所述，对于高压和高速运行的设备，若要求端面稳定性好且对密封性要求不是过于苛刻的应选用=1.0的密封端面；若要求密封更可靠且稳定性较好应选用=0.2的密封端面。

3 结 论

（1）在给定工况条件下，由菱形孔所引起的动压效应使得密封端面产生周向和径向波状变形，而静压效应随着的变化，在端面区域范围内所起作用也发生相应变化；密封端面的液膜稳定性受其液膜压强波动均匀性和强度的影响较大，压强变化越均衡，强度越大，液膜稳定性越好，z就越大，在运行过程中越平稳，难以接触，寿命周期就越长。

（2）为提高液膜稳定性和密封可靠性，对于压强较低和低、中转速的设备，应选用收敛锥面为=5～6或=2～4的机械密封，且=0.8～1.0；对于高压和高速的设备，应选用收敛锥度=2～3的密封端面，且=1.0或=0.2。

（3）锥-孔组合型机械密封具有动压和静压效应的双重作用，与单纯的动压型机械密封相比，在不同工况条件下，具有更好的z，因而适用于更广泛苛刻的工作环境。

（4）锥-孔组合型机械密封由于锥面几何的变化所引起的端面平衡系数和膜厚的变化，在低速时可以弥补动压效应较小的缺陷，获得较大o，另外也可在大下工作，故而可降低密封端面对平整度和光洁度的要求。

（5）通过改变锥面的几何结构可有效改变机械密封的特性参数，实现密封运行中的自动调节，特别适合变工况条件。

References

[2] LEBECK A O. Principles and Design of Mechanical Faxed Seals[M].Wiley Intersciene Publication, John Wiley and Son, 1991, 227-280.

[3] ZHENG X Q, BERARD G. Analysis and design of a double-divert spiral groove seal[C]// 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Joint Propulsion Conferences. Sacramento, California, 2006.

[4] ZHENG X Q, BERARD G. Development of non-contacting, low leakage, large diameter air seal[C]// 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Joint Propulsion Conferences. Hartford, CT, 2008.

[5] SALANT R F. The use of modeling to understand malfunction and failure in mechanical seals[J]. Sealing Tech., 2003, (12): 8-12.

[6] MAYER E. Mechanical Seal [M]. Beijing: Chemical Industry Press, 1981.

[7] DOUST T G. An experimental and theoretical study of pressure and thermal distortions in a mechanical seal [J]. ASLE Transactions, 1986, 29(2): 151-159.

[8] HARP S R, SALANT R F. Analysis of mechanical seal behavior during transient operation [J]. Journal of Tribology, 1998, 120(2): 191-197.

[9] 顾永泉. 机械密封端面[M].山东: 石油大学出版社, 1994. GU Y Q. Mechanical Seal Face[M].Shandong: University of Petroleum Press, 1994.

[10] 魏龙, 顾伯勤, 冯飞, 等. 接触式机械密封端面微凸体的变形特性研究[J]. 排灌机械工程学报, 2010, 28(1): 78-82. WEI L, GU B Q, FENG F,. Research on deformation property of end face asperity of contact mechanical seals [J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(1): 78-82.

[11] 彭旭东, 杜东波, 李纪云. 不同型面微孔对激光加工多孔端面机械密封性能的影响[J]. 摩擦学学报, 2006, 26(4): 367-371. PENG X D, DU D B, LI J Y. Effect of different section profile micro-pores on seal performance of a laser surface textured mechanical seal [J]. Tribology, 2006, 26(4): 367-371.

[12] 彭旭东, 刘鑫, 孟祥铠, 等. 锥面-微孔组合端面机械密封性能理论研究[J]. 化工学报, 2011, 62(12): 3463-3470.PENG X D, LIU X, MENG X K,Performance of mechanical face seals with both surface micro-pores and coning [J]. CIESC Journal, 2011, 62(12): 3463-3470.

[13] 李鲲, 姚黎明, 吴兆山, 等. 机械密封环端面变形研究[J]. 润滑与密封, 2001, (5): 44-47.LI K, YAO L M , WU Z S,. Study on face deformation of mechanical seal [J].Lubrication Engineering, 2001, (5): 44-47.

[14] 张杰, 李鲲, 吴兆山, 等. 石墨密封环端面压力变形的试验研究[J]. 润滑与密封, 2012, 37(10): 30-33, 81. ZHANG J, LI K, WU Z S,. An experimental study on pressure deformation of carbon seal ring[J].Lubrication Engineering, 2012, 37(10): 30-33, 81.

[15] 王涛, 黄伟峰, 王玉明. 机械密封液膜汽化问题研究现状与进展[J]. 化工学报, 2012, 63(11): 3375-3382. WANG T, HUANG W F, WANG Y M,. Research and progress of mechanical seals operating with vaporization transition [J]. CIESC Journal, 2012, 63(11): 3375-3382.

[16] 程香平, 孟祥铠, 彭旭东. 大菱形孔端面密封力变形及密封性能分析[J]. 化工学报, 2014, 65(8): 3089-3097. CHENG X P, MENG X K, PENG X D. Analysis of deformation and sealing performance of a mechanical face seal with diamond macro-pores[J]. CIESC Journal, 2014, 65(8): 3089-3097.

[17] 程香平, 彭旭东, 孟祥铠. 菱形孔密封环端面密封性能分析[J]. 上海交通大学学报, 2014, 48(1): 33-38. CHENG X P, PENG X D, MENG X K. Analysis of sealing performance of seal ring end face with diamond pores [J]. Journal of Shanghai Jiao Tong University, 2014, 48(1): 33-38.

[18] 程香平, 彭旭东, 孟祥铠, 等. 大圆形孔端面机械密封性能分析[J]. 润滑与密封, 2012, 37(2): 27-31.CHENG X P, PENG X D, MENG X K,. Analysis on seal performance of mechanical seals with macro-pores[J]. Lubrication Engineering, 2012, 37(2): 27-31.

[19] 程香平. 大孔径端面机械密封性能的研究[D].杭州: 浙江工业大学, 2014. CHENG X P. Performance study on end face mechanical seal with macro-pores[D]. Hangzhou: Zhejiang University of Technology, 2014.

[20] 彭旭东, 杜东波, 盛颂恩, 等. 端面微形体对液体润滑机械密封性能的影响[J].摩擦学学报, 2007, 27(4): 352-356. PENG X D, DU D B, SHENG S E,. Effect of face asperity geometry on performance of a liquid lubricated face seal [J]. Tribology, 2007, 27(4): 352-356.

Effect of tapered face parameters on performance of cone-pore-combined mechanical seal

CHENG Xiangping1, MENG Xiangkai2, PENG Xudong2, ZHANG Youliang1, FU Yuan1, KANG Linping1

(1Institute of Applied Physics, Jiangxi Academy of Sciences, Nanchang 330029, Jiangxi, China;2MOE Engineering Center of Process Equipment and Its Remanufacture, Zhejiang University of Technology, Hangzhou 310032, Zhejiang, China)

A three-dimensional fluid-solid coupling mathematic model of a cone-pore-combined mechanical seal was established by considering interactions of pressure distribution change of fluid film between two end faces and stress deformation of sealing rings. A numericaliteration method was developed to solve the coupling model so as to obtain pressure distribution of the fluid film and surface deformation. The influence of structural parameters of the tapered end face on sealing performance was analyzed at various working conditions. The results showed that diamond-shaped pores created dynamic pressure effect, which produced circular and radial wave deformation at the end faces, andstatic pressure effect, which changed impact accordingly within the end face region with the increase of taperand cone width ratio. The convergent seal of the tapered end face at=5—6 or=2—4 and=0.8—1.0 should be selected for low pressure and low to medium speed equipment. The convergent seal of the cone end face at=2—3 and=1.0 or=0.2should be selected for high pressure and high speed equipment. Changing tapered end face structure could effectively modify characteristic parameters of the cone-hole combined mechanical seal and automatically adjust seal performance during operation, which is especially suitable for variable work conditions. In addition, the change of balance coefficientand film thicknesscaused by structure change of the tapered end face could made up defects of small dynamic pressure effect at low speed to achieve large opening force andcould alsowork under largeso that the flatness and polish requirement for seal end face might be reduced.

numerical simulation; hydrodynamics; face mechanical deformation; laminar flow

2016-05-21.

CHENG Xiangping, 654268480@qq.com

10.11949/j.issn.0438-1157.20160744

TU 831.3

A

0438—1157（2016）11—4762—09

国家自然科学基金青年项目(51505203)；国家自然科学基金面上项目(51375449)；江西省科技开发和产业化开发项目(20151BBE51065)；2015年江西省科学院博士启动基金项目(2014-YYB-18，2014-XTPH1-18)。

2016-05-21收到初稿，2016-08-16收到修改稿。

联系人及第一作者：程香平(1978—)，女，博士，助理研究员。

supported by the Youth Program of the National Natural Science Foundation of China (51505203), the National Natural Science Foundation of China (51375449), the Jiangxi Province Torch Plan Foundation, China (20151BBE51065), the Doctoral Starting up Foundation of Jiangxi Academy of Sciences, China (2014-YYB-18) and Collaborative Innovation Foundation-GSP, China ( 2014-XTPH1-18).