基于八叉树自适应网格技术的Level Set运动界面追踪方法

殷亚军，李阳东，涂志新，李文，沈旭，周建新



基于八叉树自适应网格技术的Level Set运动界面追踪方法

殷亚军，李阳东，涂志新，李文，沈旭，周建新

（华中科技大学材料成形与模具技术国家重点实验室，湖北武汉430074）

Level Set方法因能有效地处理界面处复杂的拓扑结构变化以及大变形问题，广泛应用于界面追踪领域。在Level Set方法追踪运动界面时引入八叉树网格技术，通过八叉树网格的细化和粗化技术减少计算网格数量和计算内存并提高计算效率和计算精度。因为八叉树网格为非均匀网格，其相邻网格的层数值可能不相同，所以不能直接采用WENO格式离散Level Set函数得到网格处的函数值，进而提出八叉树网格离散模型解决这一问题，并提出基于八叉树网格距离场重新初始化方法减少Level Set方法的质量损失，最后将基于八叉树网格技术的Level Set方法应用于两个给定速度场的运动界面模拟算例以及基准件方腔的铸造充型过程的模拟。模拟结果表明该方法可以提高界面的精度，同时改善质量守恒性。

界面追踪；数值模拟；八叉树网格技术；Level Set方法；网格自适应；模型；优化

引 言

许多物理问题会涉及气液自由界面。采用数值模拟计算自由界面时，界面附近流体的物性会发生明显变化，需要准确追踪自由界面的位置。Level Set（水平集）方法是美国计算数学学者Osher等[1-4]提出的一种追踪界面的方法，该方法能够有效地解决复杂界面追踪问题，是目前界面追踪问题数值模拟的主流方法。

Level Set方法可以克服一般界面前沿追踪方法必须构造出具体的界面而难以处理界面前沿发生的拓扑结构变化的弱点，不需要显式追踪运动界面，从而可以较容易地处理复杂的物质界面及其拓扑结构发生变化的情形，便于计算曲率及界面法向量，可以将间断问题转化为光滑问题加以解决。与VOF（volume of fluid）法相比，该方法易于从二维问题推广到三维问题，追踪界面精度较高。

但是，经典的Level Set方法守恒性差，初始时刻Level Set为距离函数，经过有限的时间步长后不再保持距离函数的性质，需要重新初始化，重新初始化Level Set函数涉及的复杂数学过程极大地增加了计算量。此外，为了减少数值耗散，在求解Level Set方程时通常采用高阶格式离散空间导数和时间导数，这些高阶计算格式会影响其计算效率。为了提高Level Set方法的计算速率与精度，许多学者对此做了大量的研究。Osher等[5]对Level Set重新初始化方法进行了研究。Sethian等提出了Fast Marching Method (FMM，快速步进法)[6-7]对Level Set函数进行重新初始化，提出窄带方法[8]使Level Set方法更加快速有效。Peng等[9]在全局Level Set方法的基础上提出了一种快速局部Level Set方法，大大节省了计算时间。Strain[10]首先引入树型结构的自适应网格，在交界面附近采用高分辨率网格，而在远离交界面的区域保持较粗的网格。Sochnikov等[11]将Fast Marching（快速步进）技术应用到四叉树型结构的自适应网格中，使得计算量进一步减少。Costa等[12]采用了自适应网格加密（adaptive mesh refinement, AMR）技术进行结构拓扑优化。宫翔飞等[13]将Level Set方法与AMR技术融合用于数值模拟。黄筱云等提出了一种基于树型结构空间自适应的快速粒子Level Set 方法[14]，并提出自适应四叉树网格下的N-S方程数值求解模型[15]。王生辉等[16]将四叉树直角坐标网格技术与Level Set方法相结合进行运动界面的追踪。Losasso等[17]利用八叉树网格技术模拟了烟雾和水流的运动。朱雷等[18]采用八叉树网格模拟焊接温度场，对比了八叉树网格与均匀网格的计算效率，采用八叉树网格的计算时间只有均匀网格的40%。

为了进一步提高Level Set方法的计算效率以及界面精度，本研究将八叉树自适应网格技术应用于Level Set方法的求解，提出适用于Level Set方法追踪界面的八叉树自适应网格模型，并建立了基于八叉树自适应网格的Level Set函数的离散和重新初始化模型。采用八叉树网格容易进行网格的局部加密或粗化，减少网格数量以及计算量。同时，局部网格细化能够很好地提高界面追踪的准确性。本研究增加界面处网格的最大层数值，可以很大程度地提高界面追踪的精度以及减少Level Set方法引起的数值耗散，提高界面追踪的质量守恒性，这对于改善流场失真具有重大的意义。

1 八叉树网格技术

八叉树是一种用于描述三维空间的树状数据结构，其原理是将空间区域不断分解为8个同样大小的子区域，分解的次数越多，子区域就越小，一直到同一区域的属性单一为止[19]。图1所示即为一个简单的八叉树节点产生过程。图中左侧为对应的空间区域划分，不同的区域用不同颜色的正方体表示；右侧为八叉树树型结构对应的网格节点关系，图中黑色节点表示子区域的父区域，叶子表示八叉树网格的叶子单元网格。八叉树网格以八叉树作为基本理论基础，网格组织方式与之类似，树中指代的区域即为数值模拟中对应的网格（网格单元统一为正方体单元）。

2 八叉树网格自适应

Level Set 方法追踪运动界面时，界面精度和质量损失都与网格的分辨率有关，如果将网格全部细化，则会很大程度地增加计算时间和存储空间。需要自适应网格技术对界面附近的区域进行网格细化处理，对远离界面的区域进行网格粗化处理，这样既可以保证界面附近网格有较高的分辨率，提高界面区域的计算精度，又可以减少远离界面区域所占用的内存，减少计算时间和计算内存。

2.1 细化模型

采用八叉树自适应网格技术可以提高界面附近区域的网格分辨率，保证界面附近区域的计算精度。图2所示即为一个简单的网格细化实例，其中假设白色区域为运动界面，而如果网格如图左侧所示，则需将界面周围网格细化（右图中红色网格），转化为右侧图所示，才能满足计算分析要求。

2.2 粗化模型

八叉树自适应网格与均匀网格的优势就在于效率高、计算网格数少，许多局部计算区域可以用粗化网格代替众多细化网格。图3即为某一计算时刻网格粗化的例子，白色环形区域为运动界面，左边部分网格不太理想，因为中心红色显示部分网格没有必要采用细化网格，必须经过一定的粗化模型粗化，如图3右边部分，这样就无须在该红色网格区域浪费大量的计算资源。

3 Level Set方程的离散

Level Set方法的主要思想是将随时间运动的物质界面定义为一个函数的零等值面（线），即(,)=0。在任意某一时刻，只要求出值，并求出其零等值面，就能够知道此时的活动界面位置。

在两相流或自由界面追踪问题中，速度等物理量的控制方程是N-S方程，所对应的Level Set方程见式（1），其中表示Level Set函数。

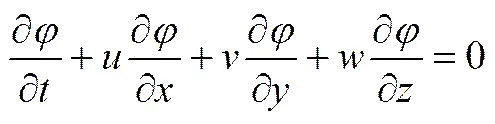
本研究采用五阶WENO格式离散Level Set函数对空间的偏导数[20]，采用三阶TVD Runge-Kutta格式离散Level Set函数对时间的偏导数[21]。

4 八叉树网格离散模型

对于均匀网格来说，采用上述离散方式直接离散Level Set函数。但是八叉树自适应网格为非均匀网格，每个网格的邻居网格层数值（层数值表征该网格的细化或粗化程度，其中树根节点网格的层数值为0，层数值越大网格单元的划分越细）可能不同，尽管单元数据仍然存储在正方体网格中心，但相邻单元网格的大小不同，不能直接采用上述的离散方式，需要对非均匀网格重新进行处理，进而获得邻居网格的Level Set函数值进行导数离散。

八叉树网格与其相邻网格之间存在3种关系：当前网格与相邻网格均为叶子单元，如图4（a）所示；当前网格为叶子单元，相邻网格为子单元网格，如图4（b）所示；当前网格为子单元网格，相邻网格为叶子单元，如图4（c）所示。其中，红色网格为当前网格，绿色网格为相邻网格。

对于图4（a）所示情况，计算当前网格Level Set函数的导数可以采用均匀网格计算方法得到，直接选取相邻网格的值进行计算。对于图4（b）所示情况，在计算当前网格Level Set函数的导数时首先计算相邻网格值，在其相邻网格的8个子单元中找出与当前计算网格面相邻的4个子单元，因为当前网格在该面的物理场变量的变化只与该面的流通量有关，故需要这4个单元才能获得相邻网格值。本研究采用一种较为简单的方式获取相邻网格值，将4个子单元对应的中心网格值取平均值计算相邻网格的Level Set函数值，然后用相邻网格值计算当前网格Level Set函数的空间导数。相邻网格值的计算如式（2）所示

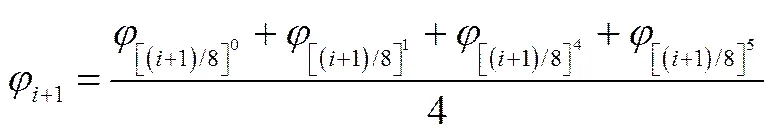
式中，+1表示导数计算时邻居网格值，、、和分别表示与当前计算网格面接触的4个邻居子单元网格值。

对于图4（c）所示情况，计算子单元网格的Level Set函数值，需要借助一定的插值方法获得邻居网格值，将相邻网格构造出8个相同的虚单元网格（图5中绿色网格），利用插值公式计算相邻虚单元网格的函数值并作为邻居网格值，然后用该虚单元的值计算当前子单元网格的Level Set函数导数值。邻居网格的插值公式如式（3）所示

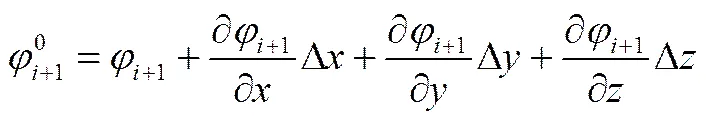
式中，0+1表示相邻虚单元网格值，+1表示相邻叶子单元网格值，D、D、D分别表示虚子单元网格中心到相邻叶子单元网格的距离。

图5 相邻虚单元网格

Fig.5 Illustration of neighbor virtural subunit grid

5 Level Set函数重新初始化

求解Level Set函数时，保持(,)为距离函数非常重要，但是Level Set方法守恒性差，经过几个计算时间步长后(,)不再保持距离函数性质，需要对时刻求解得到的(,)函数进行修正，使函数的近似值满足距离场的条件。Sussman等[3]提出了一种新的重新初始化方法

(5)

其中，(0)是函数符号。Peng等[9]采用式（5）所示格式可以得到更好的效果。本研究采用式（5）形式对Level Set函数进行重新初始化。

重新初始化Level Set函数值会发生改变，所以八叉树网格中的Level Set函数值也需要更新，八叉树网格中距离场函数更新步骤如下：①将界面处网格单元（图6中紫色网格）标记为1，其余单元标记为0，若边界位置网格不是界面单元则将其Level Set函数值设置为一个极大值；②从边界位置网格[图6（a）中绿色网格]扫描遍历网格单元，当扫描到细化网格单元如图6（b）红色圆圈中的网格[图6（b）为图6（a）中红色圈出网格的局部放大图]，本研究规定先扫描与当前扫描网格相邻的4个子单元网格，再扫描与这4个子单元网格相邻的子单元网格，在未扫描到界面单元之前这些网格单元的距离场函数值不更新；③当扫描到标记为1的界面网格单元时，直接跳过该单元，不更新该网格单元的距离场函数值，继续沿该方向扫描并更新后面标记为0的网格单元的Level Set函数值，直至扫描到下一个边界位置；④从已更新函数值的边界网格[图6（a）中绿色圆圈中的网格]的相反方向开始扫描，在扫描到界面网格之前不更新已扫描网格的函数值，当扫描到界面网格单元时直接跳过该网格，继续扫描网格单元并更新之后扫描网格单元的函数值，直至扫描到界面网格为止，如果当前扫描网格的邻居网格有多个界面网格则该网格的距离场函数值为3个方向邻居网格的最小值；⑤重复步骤②～④对其他网格进行重新初始化，直到所有八叉树网格单元距离场函数值全部重新初始化为止。

6 应 用

以基于八叉树网格技术的Level Set方法模拟不同网格细化程度的Zalesak圆球在旋转场中的运动情况以及圆球在剪切场中的运动情况为例，讨论基于八叉树网格技术的Level Set方法在三维空间的应用，并将该方法应用于追踪方腔铸件充型过程的界面前沿，模拟充型过程中液体的流动。

6.1 旋转流场

本算例模拟的是一个半径为0.25的Zalesak圆球界面在旋转流场作用下的变化情况，初始位置为[0.5,0.5,0.5]，切口宽度为0.125，切口深度为0.3125，计算区域为[0,1]×[0,1]×[0,1]，网格尺寸为128×128×128。网格的最大层数分别为8层和9层，最小网格层数为4层。旋转流场的速度场为

流场周期为2p，时间步长为0.05。

图7为Zalesak圆球在三维旋转流场中八叉树自适应网格示意图,图8和图9分别是网格最大层数为8层和9层时Zalesak圆球在旋转流场中的运动时间分别为0、/4、/2、3/4和时刻的数值模拟结果。图10为刘长春[22]采用Youngs-VOF方法模拟缺口圆在旋转流场中的运动的结果，图11为张明远[23]采用均匀网格的Level Set方法追踪Zalesak圆球运动界面的结果。

通过图8和图9的数值模拟结果可以得出：Zalesak圆球经过一个计算周期后回到了初始位置，八叉树网格最大层数为9层时Zalesak圆球表面的精度远高于网格最大层数为8层时Zalesak圆球表面的精度，而且在Zalesak圆球缺口处仍然可以保持尖锐。比较图9、图10和图11的模拟结果可以发现：图10 Youngs-VOF方法中红色圆圈中的尖锐部分有一些失真，本研究提出的方法在尖锐界面处的模拟精度略好一些；图11中绿色圆圈中界面部分质量损失严重且界面精度也较低，其中的平面部分已经平滑成为了曲面，本研究图9的模拟结果则很好地保持了原来的界面形状，提高了界面追踪的精度和质量守恒性。

6.2 剪切流场

本算例模拟的是一个半径为0.125的圆球在剪切流场作用下的变化情况，初始位置为[0.5,0.5,0.25]，计算区域为[0,1]×[0,1]×[0,1]，网格尺寸为128×128×128。网格的最大层数分别为8层和9层，最小层数为4层。剪切流场的速度场为

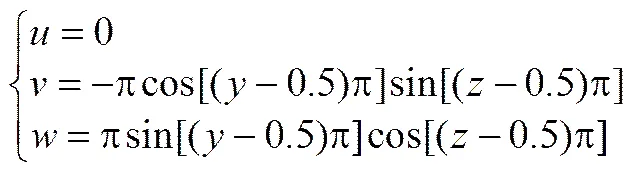
流场周期为2p，时间步长为0.05。

图12为圆球在三维剪切流场中八叉树自适应网格模型,图13和图14分别是网格最大层数为8层和9层时运动时间分别为0、/4、/2、3/4和时刻的数值模拟结果。图15为刘长春[22]采用Youngs-VOF方法模拟圆在二维剪切流场中的运动的结果，图16为张明远[23]采用均匀网格的Level Set方法追踪圆球在三维剪切流场中的运动界面的结果。

通过图13和图14的数值模拟结果可以得到：圆球在剪切流场中经过一个时间周期后又恢复到原来的形状，但是由于Level Set方法的质量守恒性差，圆球发生一些变形。比较图13和图14，增加网格最大层数可以改善Level Set方法在剪切流场中的数值模拟结果，提高Level Set方法的质量守恒性以及界面的精度。比较图14、图15和图16可以发现，图15中的界面追踪结果出现了破碎现象，其结果很不理想，图16中的均匀网格Level Set方法模拟结果的质量守恒性差，本研究提出的方法则可以较好地保持质量守恒性且界面形状保持较好。

6.3 方腔铸件充型过程数值模拟算例

为了进一步证明基于八叉树自适应网格技术的Level Set方法追踪界面运动的可行性，本算例模拟方腔铸件充型流动过程中金属液体界面的运动过程，该过程中金属液体通过浇注系统流入方腔铸件并进行充型，其计算区域为[0,1]×[0,1]×[0,1]，网格尺寸为32×32×32。

数值模拟结果如图17所示，图中红色区域表示铸型，蓝色区域表示充型金属液体，紫色区域表示铸型中的空气即待充型区域。由图17可以看出采用八叉树技术的Level Set方法可以很好地模拟铸件充型过程中液体界面的运动位置，能够较为准确地描述铸造过程中金属液体的充型流动。

7 结 论

研究了基于八叉树网格技术的Level Set方法追踪运动界面，引入八叉树技术可以改善Level Set方法模拟运动界面的一些不足，主要的研究工作总结如下。

（1）提出了适用于Level Set方法追踪界面的八叉树网格自适应模型（八叉树网格技术的细化与粗化模型），通过对局部运动网格的细化与粗化可以减少数值模拟的计算网格与内存，提高计算的效率与精度。

（2）建立了一套基于八叉树自适应网格的Level Set方法追踪运动界面求解方法，并提出了基于八叉树自适应网格Level Set函数值离散模型以及求解八叉树相邻网格距离场函数值的插值方法。

（3）提出了八叉树网格距离场重新初始化方法，通过快速扫描八叉树网格并判断网格是否为界面网格更新非界面网格单元的Level Set函数值，重新初始化八叉树网格中的距离场函数值。

（4）两个运动界面算例模拟结果表明：将八叉树技术引入Level Set方法可以成功地追踪运动界面，局部细化八叉树网格以及增加网格的最大层数可以提高Level Set方法追踪界面的精度以及质量守恒性，减少Level Set方法产生的数值耗散。并用该方法模拟铸件充型过程的金属液体流动，结果表明该方法可以较为准确地模拟铸件充型过程。

符 号 说 明

S(j0)——距离函数符号 T——运动周期，s t——时间，s Dt——时间步长，s u, v,w——分别为直角坐标3个方向的速度，s-1 x,y,z——三维直角坐标系的3个方向 Dx,Dy,Dz——分别为3个方向网格单元长度 j——Level Set 函数

References

[1] OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49.

[2] OSHER S, FEDKIW R P. Level set methods: an overview and some recent results[J]. Journal of Computational Physics, 2001, 169(2): 463-502.

[3] SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics, 1994, 114(1): 146-159.

[4] WU K T, HAO L, WANG C,. Level set interface treatment and its application in Euler method[J]. Science China Physics Mechanics & Astronomy, 2010, 53(2):227-236.

[5] CHEN S, MERRIMAN B, OSHER S,. A simple level set method for solving Stefan problems[J]. Journal of Computational Physics, 1997, 135(1): 8-29.

[6] SETHIAN J A. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences, 1996, 93(4): 1591-1595.

[7] SETHIAN J A. Evolution, implementation, and application of level set and fast marching methods for advancing fronts[J]. Journal of Computational Physics, 2001, 169(2): 503-555.

[8] ADALSTEINSSON D, SETHIAN J A. A fast level set method for propagating interfaces[J]. Journal of Computational Physics, 1995, 118(2): 269-277.

[9] PENG D, MERRIMAN B, OSHER S,. A PDE-based fast local level set method[J]. Journal of Computational Physics, 1999, 155(2): 410-438.

[10] STRAIN J. Tree methods for moving interfaces[J]. Journal of Computational Physics, 1999, 151(2): 616-648.

[11] SOCHNIKOV V, EFRIMA S. Level set calculations of the evolution of boundaries on a dynamically adaptive grid[J]. International Journal for Numerical Methods in Engineering, 2003, 56(13): 1913-1929.

[12] COSTA J C A, ALVES M K. Layout optimization with h-adaptivity of structures[J]. International Journal for Numerical Methods in Engineering, 2003, 58(1): 83-102.

[13] 宫翔飞, 张树道, 江松. 界面捕捉Level Set方法的（AMR）数值模拟[J].计算物理, 2006, 23(4): 391-395.GONG X F, ZHANG S D, JIANG S. Numerical simulation of fluid interfaces with the adaptive mesh refinement method, the ghost fluid method and the Level Set method[J]. Chinese Journal of Computational Physics, 2006, 23(4): 391-395.

[14] 黄筱云, 李绍武.空间自适应的快速粒子Level Set方法[J]. 天津大学学报, 2010, 43(11): 981-987. HUANG X Y, LI S W. Spatially adaptive fast particle Level Set method[J]. Journal of Tianjin University, 2010, 43(11): 981-987.

[15] 黄筱云, 李绍武. 自适应四叉树网格下的N-S方程数值求解模型[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(1): 58-66. HUANG X Y, LI S W. Numerical N-S equation solver based on adaptive quadtree mesh[J]. Journal of Tianjin University(Science and Technology), 2013, 46(1):58-66.

[16] 王生辉, 尤伟, 李增耀. 基于四叉树直角坐标网格的运动界面追踪方法[J]. 化工学报, 2014, 65(S1): 44-50. WANG S H, YOU W, LI Z Y. Interface-capturing method on quadtree-based adaptive Cartesian grid[J]. CIESC Journal, 2014, 65(S1): 44-50.

[17] LOSASSO F, GIBOU F, FEDKIW R. Simulating water and smoke with an octree data structure[J]. ACM Transactions on Graphics, 2004, 23(3):457-462.

[18] 朱雷, 周建新, 庞盛永, 等. 基于八叉树网格的激光焊接温度场数值模拟方法[J]. 热加工工艺, 2014, 43(5): 164-167. ZHU L, ZHOU J X, PANG S Y,. Numerical simulation method of laser welding temperature field based on octree grid[J]. Hot Working Technology, 2014, 43(5): 164-167.

[19] 殷亚军. 基于八叉树网格技术的相场法金属凝固过程组织模拟的研究[D]. 武汉: 华中科技大学, 2013. YIN Y J. Research on the microstructure simulation of the alloy solidification based on phase field method by the octree mesh technology[D]. Wuhan: Huazhong University of Science and Technology, 2013.

[20] 刘元元. WENO方法的研究及其在对流扩散方程中的应用[D]. 合肥: 中国科学技术大学, 2012. LIU Y Y. WENO methods and the applications in convection diffusion equations[D]. Hefei: University of Science and Technology of China, 2001.

[21] 郑素佩, 欧阳洁, 张红平, 等. 带有矩形嵌件薄壁型腔内熔接过程动态模拟[J]. 化工学报, 2008, 59(1): 232-238. ZHENG S P, OUYANG J, ZHANG H P,. Dynamic simulation for weld lines in thin mold with rectangle cylinder[J]. Journal of Chemical Industry and Engineering (China), 2008, 59(1): 232-238.

[22] 刘长春. Level Set方法模拟界面运动[D]. 北京: 中国科学院工程热物理研究所, 2007. LIU C C. Level Set methods for moving interfaces[D].Beijing: Institute of Engineering Thermophysics, Chinese Academy of Sciences, 2007.

[23] 张明远. 基于Projection方法的铸造充型过程数值模拟[D].武汉: 华中科技大学, 2011. ZHANG M Y. Numerical simulations of casting’s filling process based on a Projection method[D]. Wuhan: Huazhong University of Science and Technology, 2011.

Interface capturing method based on Level Set with octree adaptive mesh technology

YIN Yajun, LI Yangdong, TU Zhixin, LI Wen, SHEN Xu, ZHOU Jianxin

(State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Technology, Wuhan 430074, Hubei, China)

Level Set method is one of the dominant methods to calculate and track evolution of interfaces because it can efficiently handle complex topology change of interfaces and large deformation. This method often suffers from large amount of numerical dissipation and high order accurate numerical discretization in time and space is used to improve mass conservation properties, which leads to an increase of computational overhead. When octree adaptive mesh technology is incorporated into Level Set to capture moving interfaces, the amount of computational meshes and memory usage is reduced and the calculation precision and efficiency are enhanced by adaptive octree mesh refining or coarsening according to interface distance. Because octree mesh is non-uniform and layer numbers of neighbor grids may be different, the WENO formula could not be directly applied to set values of octree grids. A discretization model and a technique of re-initializing distance field were proposed to calculate value of neighbor octree grids as well as to reduce mass loss in Level Set function. Numerical simulation on moving interface in rotation flow field of Zalesak sphere, in shear flow field of sphere and in cast filling process of square cavity benchmark indicated that combination of Level Set method and octree adaptive mesh technology could successfully capture moving interface. The interface-tracking precision was enhanced by refinement of octree meshes and increase of maximum octree mesh layers. When the maximum octree mesh layer was increased from 8 to 9 in the shear flow field, mass conservation of the sphere was obviously improved and numerical dissipation caused by Level Set method was significantly reduced.

interface capture; numerical simulation; octree mesh technology; Level Set method; adaptive mesh; model; optimization

2016-04-05.

Prof. ZHOU Jianxin,zhoujianxin@hust.edu.cn

10.11949/j.issn.0438-1157.20160421

O 351.2

A

0438—1157（2016）11—4732—10

殷亚军（1985—），男，博士，讲师。

国家自然科学基金项目（51475181，51305149）；中国博士后科学基金特别资助项目（2015T80795）。

2016-04-05收到初稿，2016-08-03收到修改稿。

联系人：周建新。

supported. by the National Natural Science Foundation of China(51475181, 51305149) and the China Postdoctoral Science Foundation Special Funding(2015T80795).