基于基团拓扑的遗传神经网络工质临界温度预测

苏文，赵力，邓帅



基于基团拓扑的遗传神经网络工质临界温度预测

苏文，赵力，邓帅

（天津大学中低温热能高效利用教育部重点实验室，天津300072）

用遗传神经网络预测工质的临界温度，网络的输入参数为分子基团和拓扑指数，输出参数为临界温度。所划分的16个分子基团涵盖了制冷、热泵及有机朗肯循环系统中的大部分工质，所选拓扑指数能够分辨工质中所有的同分异构体。通过遗传算法优化得到网络结构及初始参数后，由神经网络对工质临界温度进行预测，同时为了提高网络对临界温度预测的泛化能力，将200种工质划分成训练集、验证集及测试集。所得网络能够区分所有的同分异构体，且与实验值相比，各数据集临界温度的平均相对误差分别为1.18%、1.69%、1.28%，表明该网络对工质临界温度具有很好的预测能力。

热力学性质；临界温度；工质；分子基团；拓扑指数；遗传算法；神经网络

引 言

工质作为实现热力循环热功转换的流动介质，其基础物性是热力循环构建、控制和优化的基础，同时也决定着循环系统的安全性、经济性。虽然，已有文献都收集有大量可靠的热物性数据[1-2]，但随着人们对温室效应及臭氧空洞等环境问题的日益重视，研发高效、低ODP（ozone depletion potential）、低GWP（global warming potential）的循环工质迫在眉睫。通过分子设计逆向工程，高效率地寻找具有特定性质的分子已成为工质研发的主要手段[3]。分子设计的主要依据是分子构效关系，关键在于建立高精度的结构-物性预测模型。

作为亚临界与跨临界热力循环的分界点，工质临界温度(c)不仅是工质重要的基础物性，也是估算工质其他物性的基础[4]。目前，估算物性最通用的方法便是基团贡献法[5-8]。在临界温度方面，Joback等[9]提出了估算有机物临界温度的基团法；Constantinou等[10]在UNIFAC基团的基础上，发展了一种考虑邻近基团影响的基团法，提高了预测精度；Marrero等[11]论述了键贡献法，采用单一原子形成原子对的值，预测了临界温度。国内方面，许文[12]建立了估算临界温度的三基团参数关联式；马沛生等[13]在系统整理大量临界温度数据的基础上 ,提出了新基团估算法及基团贡献值，提高了估算精度；Wang等[14]提出了定位分布贡献法，其能够区分大部分的同分异构体。但以上提出的方法针对的是全体有机物，缺乏对工质展开有针对性的研究，且已有方法不能完全区分异构体，基团划分复杂，不利于分子设计中的物性快速估算。因此，本文引入了拓扑指数以区分异构体，并划分了工质基团。

近年来，由于神经网络的高度非线性功能，已成为物性预测的有力工具[15]。众多学者将神经网络和基团贡献法相结合，估算了有机物的沸点、临界参数等重要物性[16-18]。其中，旷戈等[19]提出了估算有机物临界温度的基团贡献人工神经网络集成法。但在相关研究中发现，神经网络具有网络结构难以确定，容易陷入局部极小点等固有缺陷[20]。因此，本文将进化计算中的遗传算法引入神经网络，通过分子基团及拓扑指数，实现对工质临界温度的预测。

1 分子基团及拓扑指数

1.1 基团划分

工质研究最早始于19世纪30年代，Midgely等[21]从元素周期表出发，在综合考虑工质热物理性能、毒性、稳定性等条件下，认为工质应由C、H、N、O、F、Cl、Br、I 8种元素构成。但随着环境的恶化，工质正从最初的CFC、HCFC等氟氯工质向具有低ODP、低GWP的环保型工质发展，氟氯工质逐渐被淘汰。因此，基于分子基团的工质构效关系，采用分子设计逆向思维研发符合应用需求的高效工质已引起各国学者的广泛关注[22]。根据已有工质构型及分子设计结果[23]，可以得出热力循环中有机工质主要由烷烃、烯烃、卤代烃、醚、醇、胺六类有机物构成，同时考虑分子基团划分的简易性，将工质按照官能团划分为16个基团，如图1所示。

1.2 拓扑指数

引入分子拓扑指数EATII辨别工质中存在的大量同分异构体。EATII是从分子结构图中衍生出来的一种数学量，依据分子拓扑结构及分子组成计算得到[24]，不仅与物质性质具有较好地相关性，也对不同的分子结构具有唯一性，能唯一地区分22个碳原子内形成的所有异构体[25]。图2表示拓扑指数EATII计算流程，所需的基团共价半径Radii和连接度如表1所示。

表1 基团共价半径及连接度

2 遗传神经网络

神经网络是由具有适应性的简单单元组成的广泛并行互连网络，其3层 BP （back propagation）网络能以任意精度逼近任意有理函数[26]。因此，本文采用包括输入层、隐层和输出层的BP神经网络建立基团、结构与临界温度之间的非线性关系。输入层由17个节点构成，分别代表16个基团和1个拓扑指数，其中基团输入值为该基团在分子中出现的次数。输出层只有一个节点，表示临界温度。同时，利用遗传算法(GA)优化得到网络的隐层节点数和初始参数值。200种不同工质用于建立遗传神经网络，碳元素最多为8个，临界温度值来源于美国Chemical Abstracts Service，并且所有的数据在使用前都作归一化处理。

2.1 遗传算法

遗传算法GA最早由Holland[27]提出，采用全体进化的方式，将优化问题的解以某种形式编码，产生个体，由适应度函数指导搜索方向，再通过选择、交叉、变异操作产生新一代个体，如此反复进行，直到搜索到最优解为止。为使GA能同时优化BP网络的初始参数值和隐层节点数，本文采用递阶编码机制，每个个体的染色体由控制基因和参数基因构成。控制基因决定每个隐层神经元是否被激活，采用二进制编码；参数基因用来表示每个神经元权值和阀值，采用实数编码[28]。GA的适应度函数由网络的误差函数和复杂度函数构成，误差函数MSE可由式(1)算得

式中，为工质总数；exp,i为临界温度实验值，cal,i为临界温度计算值。

网络复杂度函数由隐层节点个数决定，假设隐层节点数为，则复杂度函数NC如式(2)所示[29]

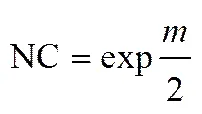
由于GA总是朝着适应度函数增大的方向迭代，因此个体适应度函数ƒ定义如式(3)所示

(3)

对于遗传算子，本文采用正常几何分布的选择算法、线性组合的算术交叉算法和所有基因随机扰动的非均匀变异算法。同时考虑到工质总数为200，设最大隐层节点数为15，种群大小为100，最大迭代次数为500。遗传算法流程如图3所示。

2.2 BP神经网络

基于误差反向传播的BP网络主要由正向传播和反向传播两部分组成。在正向传播中，输入参数从输入层经隐含层神经元处理后，传至输出层，如果输出层得到的不是期望输出，就转为反向传播，依据网络的实际输出和期望输出之间误差的负梯度方向，从后往前逐层地迭代修正各层神经元之间的连接权值和阀值。基于GA得到的网络初始参数及隐层节点数，本文采用收敛快且精度高的Levenberg-Marquardt(LM)学习算法对3层BP网络进行训练[30]。网络神经元的传递函数主要有3类，分别为purelin、logsig、tansig，其中传递函数tansig在定位分布贡献法被用来预测物质的临界温度[14]。因此，本文隐层和输出层分别采用传递函数tansig和purelin，定义如下

(5)

式中，表示函数参数。

为提高BP网络预测临界温度的泛化能力，防止网络出现数据过拟合，本文将200种工质分为3类，分别为训练集、验证集、测试集，比例依次为70%、15%、15%[30]。BP网络算法流程如图4所示。

3 结果与讨论

通过遗传算法得网络最优隐层节点数为6，因此，BP网络的拓扑结构为17-6-1。利用LM算法从GA得到的初始参数开始对该网络进行训练，得到如表2所示的网络优化值。同时，根据BP网络传递函数，建立基团、结构与临界温度之间的关系，得式(6)

式中，W是隐层神经元的权重；W是基团对神经元的输入权重；W是拓扑指数EATII对神经元的输入权重；是隐层神经元常数；C是基团常数；N是工质所含基团的个数。和C列于表2。

表2 网络优化值及参数

训练所得BP网络预测临界温度的性能可由以下统计参数评价

(8)

(9)

其中AARD是平均相对误差，用来表示网络计算值偏离实验值的程度；bias是平均偏差，用以描述计算值在实验值两侧的平均分布；RMS是计算值与实验值之间的绝对平均差。

图5分别给出了训练集、验证集、测试集的临界温度计算值与实验值之间的比较。相关系数用以反映计算值与实验值之间的密切关系程度。对于训练集、验证集、测试集，分别为0.9951、0.9926、0.9976，说明由BP网络计算的临界温度值和实验值之间具有很好的一致性。每个集合的统计参数列于表3，对于200种工质，AAD、bias、RMS分别为1.27%、0.09%，9.0877。每种工质临界温度的相对误差ARD定义如式(10)所示

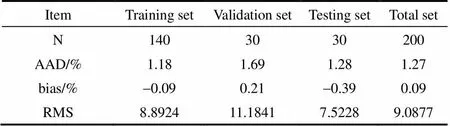
表3 各数据集的统计参数

图6给出了200种工质的相对误差分布情况，其中ARD>5%的工质只有6种，最大误差为12.4%，而ARD≤2%的工质有157种，占比78.5%。

对于工质中存在的大量同分异构体，表4给出了预测示例。当基团和工质结构都不一样时，同分异构体的性质差异通过基团个数和拓扑指数进行区分。对于基团相同、结构不同的异构体，在低碳分子中，由于临界温度相差很小，则忽略EATII之间的差别。但随着碳原子数的增多，EATII之间的差别逐渐增大，对异构体的区分能力增强。因此，对于具有大量同分异构体的有机工质而言，本文建立的BP神经网络能有效区分异构体间的物性差异。

表4 工质同分异构体的预测

4 结 论

本文基于分子基团及拓扑指数，采用遗传神经网络，预测了工质的临界温度，发展了相应的关联式。对网络预测结果分析，得到以下结论。

（1）建立的网络模型能准确的预测工质临界温度，对训练集、验证集和测试集的平均相对误差分别为1.18%、1.69%、1.28%。

（2）所选拓扑指数与物质性质具有良好的相关性，能够区分所有的工质异构体，使得网络能够有效地预测同分异构体。

（3）该模型能仅根据分子结构预测新型工质的临界温度，有利于工质分子设计中的物性快速估算。

符 号 说 明

AARD——平均相对误差，% ARD——相对误差，% bias ——平均偏差，% EATII ——拓扑指数 f——适应度函数 MSE——误差函数 m——隐层节点数 N——工质总数 NC——复杂度函数 T——温度，K RMS——绝对平均差 下角标 c——临界温度 cal——网络计算临界温度值 exp——工质临界温度实验值 i——第i种工质或第i个数

References

[1] 侯虞钧.化学工程手册[M].北京:化学工业出版社,1986. HOU Y J. Chemical Engineering Handbook[M]. Beijing: Chemical Industry Press, 1986.

[2] CALM J, HOURAHAN G. Physical, safety and environmental data for current and alternative refrigerants[C]// Proceedings of 23rd International Congress of Refrigeration (ICR2011). Prague, Czech Republic, 2011.

[3] SAMUDRA A, SAHINIDIS N. Design of secondary refrigerants.A combined optimization enumeration approach[C]//Proceedings of AIChE Annual Meeting, Philadelphia, 2009.

[4] POLING B.E, PRAUSNITZ J M, CONNELL J P. The Properties of Gases and Liquids[M]. 5th ed. New York: McGraw-Hill, 2004.

[5] 王小艳, 司继林, 张达, 等. 纯物质临界参数估算方法的研究进展[J]. 化工进展, 2012, 31(9): 1871-1877. WANG X Y, SI J L, ZHANG D,. Research progress of estimation methods for critical parameters of pure substances[J]. Chem. Ind. Eng. Prog., 2012, 31(9): 1871-1877.

[6] 夏力,李忠杰,项曙光.估算有机物正常沸点的元素和化学键贡献法[J].化工进展,2007, 26 (1): 138-144. XIA L, LI Z J, XIANG S G. A new method based on elements and chemical bonds for estimating normal boiling point of organic compounds [J]. Chem. Ind. Eng. Prog., 2007, 26(1): 138-144.

[7] 周永昌, 赵锁奇, 许志明, 等. 预测复杂高沸点重质油馏分平均沸点的基团贡献法[J]. 化工学报, 2004, 55(8): 1224-1229. ZHOU Y C, ZHAO S Q, XU Z M,. New group contribution method for estimating average boiling point of heavy oil fractions[J]. Journal of Chemical Industry and Engineering(China), 2004, 55(8): 1224-1229.

[8] 陈福明. 基团溶解度参数及有机物汽化热的估算[J]. 化工学报, 1991, 42(3): 328-333. CHEN F M. Estimation of the group solubility parameter and the latent heat for organic compounds[J]. Journal of Chemical Industry and Engineering(China), 1991, 42(3): 328-333.

[9] JOBACK K G, REID R C. Estimation of pure-component properties from group-contributions[J]. Chemical Engineering Communications, 1987, 57(1-6): 233-243.

[10] CONSTANTINOU L, GANI R. New group contribution method for estimating properties of pure compounds[J]. AIChE Journal, 1994, 40(10):1697-1709.

[11] MARRERO J, PARDILLO E. Estimation of pure compound properties using group-interaction contributions [J]. AIChE Journal, 1999, 45(3): 615-621.

[12] 许文. 估算有机物基础物性的三基团参数关联式[J]. 化工学报, 1992, 43(2): 222-229. XU W. Estimation of three group parameters for correlating basic physical properties of organic compounds[J]. Journal of Chemical Industry and Engineering(China), 1992, 43(2): 222-229.

[13] 马沛生, 王加宁, 李平. 基团法估算临界参数的改进[J]. 高校化学工程学报, 1996, 10(4):15-18. MA P S, WANG J N, LI P. Improvement of group contribution method for estimation of critical parameters[J]. Journal of Chemical Engineering of Chinese Universities, 1996, 10(4): 15-18.

[14] WANG Q, MA P, JIA Q,. Position group contribution method for the prediction of critical temperatures of organic compounds[J]. Journal of Chemical & Engineering Data, 2008, 53(5): 1103-1109.

[15] 许禄, 胡昌玉. 化学中的人工神经网络法[J]. 化学进展, 2000, 17(1): 18-31. XU L, HU C Y. Artificial neural networks in chemistry[J]. Progress in Chemistry, 2000, 17(1): 18-31.

[16] 张维涛, 于雁武. 基团贡献人工神经网络集成法估算有机物物性研究进展[J].中国胶粘剂, 2015, 24(4): 46-48. ZHANG W T, YU Y W. Research progress of group contribution method integrated with artificial neural network for estimating the properties of organic compounds[J]. China Adhesives, 2015, 24(4): 46-48.

[17] 彭黔荣, 杨敏, 石炎福, 等. 基于混合遗传算法的人工神经网络模型及其对有机化合物熔点的预测[J]. 化工学报, 2005, 56 (10) :1922-1927. PENG Q R, YANG M, SHI Y F,. Artificial neural network based on hybrid genetic algorithm and prediction of melting points of organic compounds[J]. Journal of Chemical Industry and Engineering(China), 2005, 56(10):1922-1927.

[18] 张向东, 赵立群, 张国义. 人工神经网络法预测有机物基础物[J]. 化工学报, 1995, 46(1): 66-74. ZHANG X D, ZHAO L Q, ZHANG G Y. An artificial neural network for predicting the basic physical properties of organic compounds[J]. Journal of Chemical Industry and Engineering(China), 1995, 46(1): 66-74.

[19] 旷戈, 赵素英, 赵之山, 等. 人工神经网络基团贡献法估算纯有机物的临界参数[J]. 计算机与应用化学, 2001, 18 (4): 396-9. KUANG G, ZHAO S Y, ZHAO Z S,. Prediction of critical properties for organic compound by group-contribution artificial neural network method [J]. Computers and Applied Chemistry, 2001, 18(4): 396-399.

[20] 刘春艳, 凌建春, 寇林元, 等. GA-BP神经网络与BP神经网络性能比较[J]. 中国卫生统计, 2013, 30 (2):173-6.LIU C Y, LING J C, KOU L Y,. Performance comparison between GA-BP neural network and BP neural network[J]. Chinese Journal of Health Statistics, 2013, 30 (2):173-176.

[21] MIDGLEY T, HENNEAL, MCNARY R R. Heat transfer and refrigeration: US 2104882 [P]. 1938-01-11.

[22] 李素芳, 陈腊生. 分子设计的发展与应用[J].化学世界, 2005, 46(9): 574-575. LI S F, CHEN L S. Development and application of molecular design[J]. Chemical World, 2005, 46(9): 574-575.

[23] KHETIB Y, LARKECHE O, MENIAI A,. Group contribution concept for computer-aided design of working fluids for refrigeration machines[J]. Chemical Engineering & Technology, 2013, 36(11): 1924-1934.

[24] GUO M, XU L, HU C Y,. Study on structure-activity relationship of organic compounds-applications of a new highly discriminating topological index[J]. Match, 1997, 14(35): 185-197.

[25] 许禄, 胡昌玉, 许志宏. 应用化学图论[M]. 北京: 科学出版社, 2000. XU L, HU C Y, XU Z H. Apply Chemistry Graph Theory[M]. Beijing: Science Press, 2000.

[26] NIELSEN R. Theory of the back propagation neural network[J]. Neural Networks, 1988, 1(1): 65-93.

[27] HOLAND J H. Adaptation in Natural and Artificial Systems[M]. Ann Arbor: The University of Michigan Press, 1975.

[28] 孙娓娓.BP 神经网络的算法改进及应用研究[D]. 重庆: 重庆大学, 2009. SUN W W. Study on improved algorithm and application of BP neural network[D]. Chongqing: Chongqing University, 2009.

[29] 赵寿玲. BP神经网络结构优化方法的研究及应用[D]. 苏州: 苏州大学, 2010.ZHAO S L. Researches and application on the structure optimization of the BP neural networks[D]. Suzhou: Soochow University, 2010.

[30] MOOSAVI M, SEDGHAMIZ E, ABARESHI M. Liquid density prediction of five different classes of refrigerant systems (HCFCs, HFCs, HFEs, PFAs and PFAAs) using the artificial neural network-group contribution method[J]. International Journal of Refrigeration, 2014, 48:188-200.

Prediction of refrigerant critical temperature with genetic neural network based on group topology

SU Wen, ZHAO Li, DENG Shuai

(Key Laboratory of Efficient Utilization of Low and Medium Grade Energy, Ministry of Education, School of Mechanical Engineering, Tianjin University, Tianjin300072, China)

A genetic neural network was presented to predict the critical temperature of refrigerants. The inputs of the network included molecular groups and a topological index, and the output was the critical temperature. 16 molecular groups divided can cover most of the refrigerants or working fluids in refrigeration, heat pump and Organic Rankine Cycle research. The chosen topological index was able to distinguish all refrigerant isomers. The critical temperatures of refrigerants were estimated by the neural network after obtaining the optimized network structure and initial parameters by genetic algorithm. At the same time, in order to improve network generalization ability of prediction, 200 data points were divided into three data sets including the training, validation, and test sets. The calculated results based on the developed network showed a good agreement with experimental data. The network can distinguish all refrigerant isomers and compared with the experimental data. The average absolute relative deviations for training, validation and test sets were 1.18%, 1.69% and 1.28%, respectively.

thermodynamics property; critical temperature; refrigerant; molecular groups; topological index; genetic algorithm; neural network

2016-03-11.

Prof. ZHAO Li, jons@tju.edu.cn

10.11949/j.issn.0438-1157.20160289

TK 123

A

0438—1157（2016）11—4689—07

苏文（1991—），男，博士研究生。

国家自然科学基金项目(51276123, 51476110)。

2016-03-11收到初稿，2016-08-25收到修改稿。

联系人：赵力。

supported by the National Natural Science Foundation of China (51276123, 51476110).