考虑供给商品价格的多车场车辆路径问题

鲁建厦，洪欢蕾，陈青丰

(浙江工业大学 工业工程研究所，浙江 杭州 310014)



考虑供给商品价格的多车场车辆路径问题

鲁建厦，洪欢蕾，陈青丰

(浙江工业大学 工业工程研究所，浙江 杭州 310014)

针对在烟草、石油和食品等生产配送行业，由于各地生产成本不同，导致商品由不同工厂所生产配送的补给价格存在差异，为了在车辆调度问题中综合考虑供给成本和运输成本，并使得总成本最小化，开展了考虑商品供给价格的多车场车辆路径问题研究.建立了基于分布式生产销售系统考虑商品供给价格的多点配送车辆路径优化模型；为了求解优化模型，同时根据考虑供给价格的多车场车辆路径问题的性质和特征，构造出初始解，并结合8个邻域结构和局部搜索算法，设计了改进变邻域搜索算法；最后通过实例，验证了算法的有效性.

供给价格；多车场车辆路径问题；变邻域搜索

多车场车辆路径问题一直是困扰学者的一类典型的NP难题，由于社会化物流需求不断提高，物流成本占生产制造成本的比例一直居高不下，因此引起了国家、企业和学术界广泛的关注.Dantzig等[1]在1959年最早把车辆路径问题(Vehicle routing problem ，VRP)作为“卡车调度问题”进行研究.

针对多车场车辆路径问题，Golden等[2]针对MDVRP提出了两种解决方法，一是改进后的节约里程法，二是“先分配，后路线”的两阶段方法.Cordeau等[3]研究了有时间窗约束的多车场路径问题(Multiple-depot vehicle routing problem with time window, MDVRPTW)，并提出了统一的禁忌搜索框架.Polacek等[4]使用了变邻域搜索算法来求解MDVRPTW，在计算过程中，首先采用Cross-Exchange算子产生邻域解，然后利用加强的3-Opt算子来执行局域搜索.赵燕伟等[5]研究了多车型同时取送货的多车场低碳路径问题，并采用了量子进化算法进行求解.魏云飞等[6]研究了非满载车辆调度问题，提出了免疫遗传算法.陈晓眯等[7]研究了需求不确定下的带时间窗车辆调度问题，并提出了一种混合禁忌搜索算法进行求解.金盼等[8]研究了多目标带时间窗的多车场车辆路径问题，并提出了一种全局搜索的混合多目标进化算法.学者们研究这些问题时，假设所有配送中心的补给价格都相同，但实际上，许多生产销售配送行业普遍存在同样的商品，各配送中心供应商提供的价格不同.这样供应价格低的配送中心就应该服务更多的客户，这样才可以使供给成本和运输成本之和在整体上达到最优化.因此在车辆调度问题中应综合考虑供给成本和运输成本，使得成本最小化，为此提出了考虑商品供给价格的多车场路径问题，即每个配送中心提供的商品价格允许存在差异，是另一种MDVRP理论扩展范畴，更符合生产销售实际需求.

1 考虑供给商品价格的车辆路径问题建模

1.1 考虑供给商品价格的车辆路径问题描述

G=(V，E)表示无向连通图，其中V为无向连通图中的所有节点集合(包括配送中心和客户点)，E为网络中所有弧的集合.目标是在满足所有客户点需求及每辆车的装载量不超过其最大容量的条件下，使得商品的供给成本和运输路径成本之和最小.

1.2 问题模型建立

考虑商品供给价格的多车场车辆路径模型为

(1)

约束条件分别为

(2)

(4)

(5)

(6)

(7)

(8)

h∈H,WK∈Kh,i∈V,j∈V,i≠j

(9)

(10)

(11)

其中：式(1)为目标函数，由供给成本和配送成本两部分组成；式(2)表示各配送中心使用车辆的数目低于配送中心所拥有的车辆数目；式(3)表示车辆从配送中心出发并返回原来的配送中心；式(4)表示每个客户点只能被一辆车服务一次；式(5)确保同一车辆服务同一客户两次的情况不存在；式(6)表示车辆不能从一个配送中心到另一个配送中心；式(7)为车辆容量约束；式(8)表示车辆在车场时的时间点等于零；式(9)对于同一车辆服务的两个用户，到达后一用户的时间要大于车辆到达前一用户的时间点加上两用户之间的行驶时间，从而限制子路径的出现，式(10)为车辆行驶时间约束；式(11)表示车辆到达用户的时间点大于零.

2 改进变邻域搜索算法设计

由Mladenovic和Hansen(1997年)提出的变邻域搜索算法(VNS)属于启发式算法，它是局部搜索算法的衍生，多用来求解组合优化问题.针对大规模的VRP问题，VNS算法具有优良的寻优性能，一个有效的启发式算法，在近几年的文献中，被广泛的用于求解车辆路径问题.由于传统的局部搜索算法在迭代的过程中，通常只会设计单个邻域结构生成邻域解，再对邻域解进行局部搜索获得最优解.单个邻域结构的设计使得传统的局部搜索算法很容易陷入局部最优解，导致算法得到全局最优的概率大大降低.所以将设计一个改进的变邻域搜索算法来解决考虑商品供给价格的多车场车辆路径问题.

2.1 算法框架设计

图1为改进变邻域搜索算法的基本框架.算法的改进之处主要包含以下4个方面：1)初始解的构造阶段，首先采用聚类法完成客户点的分配，然后再用节约算法完成路径的初始化；2) Shaking过程中，设计了8种不同的邻域结构，以扩大搜索范围，同时采用交换算子和插入算子；3)在Local Search过程中，采用2-Opt和Or-Opt两种算子；4)引入模拟退火算法，用于在一定条件下接受部分较差解，减少算法陷入局部最优的可能性.

图1 改进变邻域算法框架图Fig.1 Improved VNS flowchart

2.2 初始解的生成

初始解的生成方法为先聚集后路径的方法.点的聚类过程采用的是类似三标准聚集算法[9]，由于需要同时考虑配送中心供给成本和车辆路径之间的关系，把供给成本这一因素加入到聚类的构造过程中，在计算平均距离和最近距离时，同时考虑供给成本项.具体聚集流程如下：

Step 1 初始化Nu=N，其中集合Nu为所有没有聚集的需求点集.

Step 2 重复一下步骤，直到Nu为空.

Step 3 以每个配送中心为中心，包含分配到各配送中心的客户点构成聚类，配送中心的数量即为聚类的数量.

Step 4 计算平均路径成本和补给成本之和.计算每个客户点Ni∈Nu与各个聚类之间的平均距离Lih，并用Cih=Lihβ+Diαh来表达客户点Ni加入聚类h所增加的成本值.令Ci1为客户点Ni加入到各个聚类后增加成本最少的聚类，Ci2为增加成本第二少的聚类，从Nu中选取满足Ci2-Ci1≥0.1Ci2的客户点组成集合Ns.如果Ns为空，则跳转至Step 5；否则，从集合Ns中选择Ci2-Ci1差值最大的客户点Ni，并将Ni分配至增加成本最少的聚类中，Nu=Nu∕{Ni}，跳转至Step 2.

Step 5 计算最近距离.对于余下的每个客户点Ni∈Nu，如果聚类A的某个客户点与Ni的距离最近，则将Ni分配至聚类A中，Nu=Nu∕{Ni}，跳转至Step 2.

在点的聚类过程完成后，采用节约算法[9]对每个聚类进行路径的初始化.

2.3 邻域结构的设计

Polacek等[4]设计了由12个邻域结构组成的邻域结构集合，这个邻域结构集合针对的问题也是多车场车辆路径问题，针对每个邻域结构都指定了相应供应点数和变化子路径的最大长度，但是其中并没有指定Shaking过程中的操作算子，由于需要考虑商品供应价格存在差异的特殊性，将对其设计的邻域结构做相应修改，得到表1所示的邻域结构.

表1 邻域结构集合1)

注：1)p为参与路径交换的车场的数量值；Cr为分配给路径r的客户点数.

该邻域结构包含了4个主要度量：1)变化子路径所属的供应点p的数量，2)变化子路径的数量，3)操作算子的选择，4)变化子路径的最大长度.由于车辆路径问题中考虑了货物的不同供给价格，显然供给价格低的供应点需要服务更多的客户点，所以当两条变化路径在两个不同的供应点，并且子路径长度不大于2时，采用插入算子，被选中的子路径从供给价格高的路径插入到供给价格低的路径中去.

2.4 Shaking过程

Shaking过程的作用主要是通过先前已经设计好的邻域结构，将当前解经过操作算子变换出一个新的解，来扩展当前解的搜索空间，以降低整个算法陷入局部最优的可能性.Shaking过程并没有改变当前解的大部分特征，而这也就可以在一定程度上使算法的收敛速度加快.

插入算子包括原序插入和反转插入，交换算子也可分为原序交换和反转交换，分别如图2，3所示，其中Depot代表配送中心.图2所示插入算子的操作对象为属于不同配送中心的两条变换路径；图3所示交换算子的两条变换路径可以来自同一个配送中心，也可以来自不同的配送中心.Shaking过程中反转算子的概率一般设置的较小，由于车辆行驶路径都具有方向性，所以在子路径的交换过程中都会尽可能保持子路径的原有方向，以提高获得可行解的概率.两种反转算子的概率都为picross，原序算子的概率为1-picross.picross的取值可以设定为1/K，其中K为所有配送中心拥有车辆的总数.

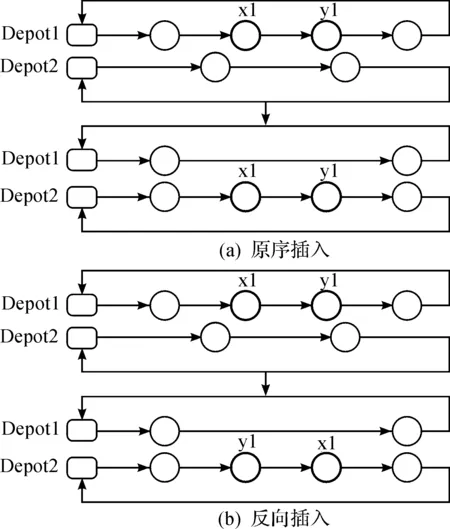
图2 插入算子操作示例Fig.2 Insert operator

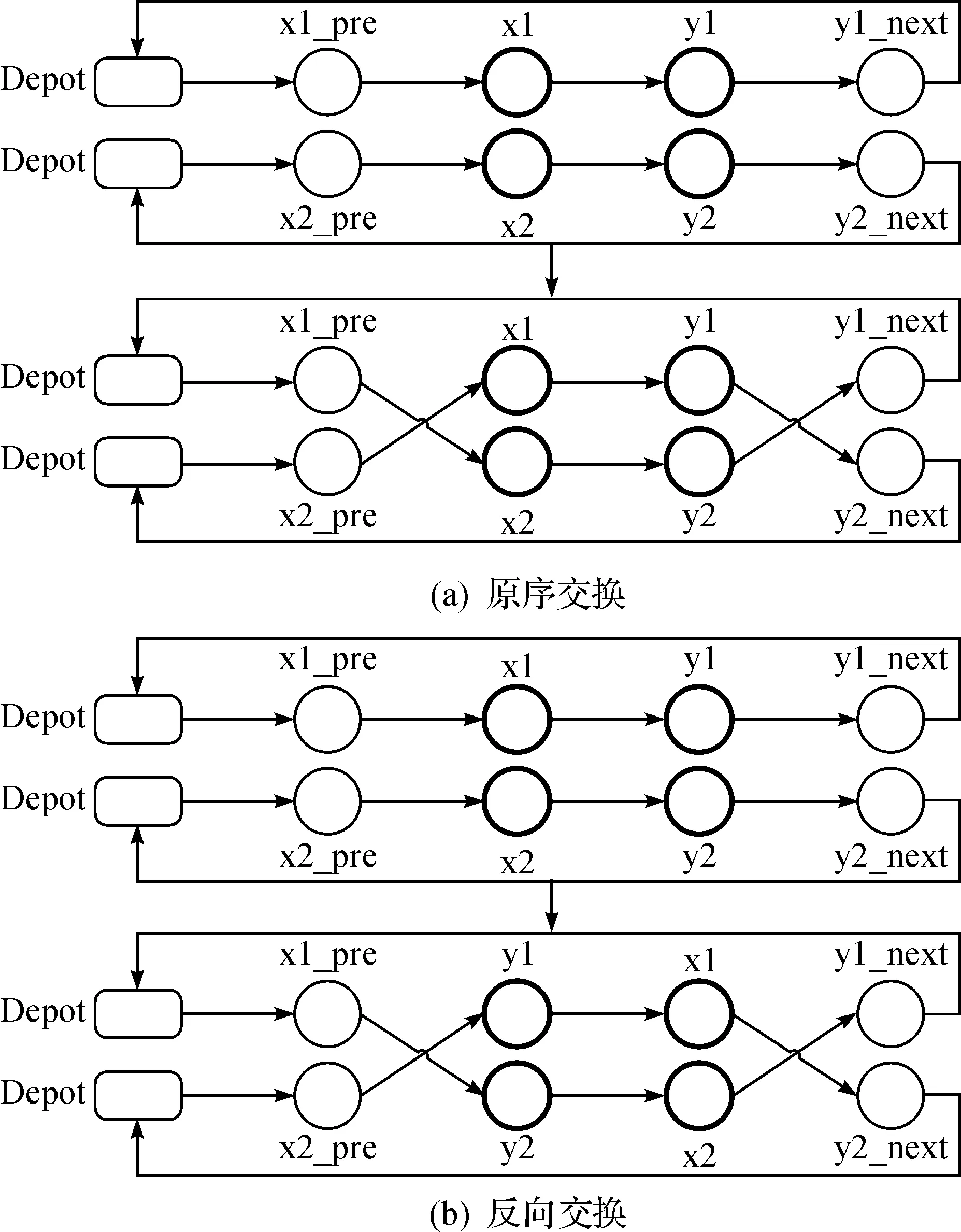
图3 交换算子操作示例Fig.3 Change operator

2.5 Local Search(局部搜索)过程

局部搜索过程的作用是对Shaking过程中所获得的两条新路径进行局部搜索操作，并分别求出两条新路径的最优解，以获得算法的局部最优解.局部搜索过程最主要的部分是局部搜索算子的设计，好的局部搜索算子能使算法在一个合理的时间内得到较理想的局部最优解，也同时决定了整个变邻域搜索算法的最终求解效率.

常用的局部搜索算子包括：2-Opt，Or-Opt，3-Opt和2-Opt*等，王征等[7]经过大量实验显示：3-Opt获得的解要优于2-Opt和Or-Opt，但其运行时间往往过长；Or-Opt则可以在较短的时间内获得求解质量较好的解；2-Opt使得子路径的方向发生改变，可以寻找反方向的较优解.综上所述，选择2-Opt和Or-Opt算子，以达到能在合理时间内获得较优解的目的.这两个局部搜索算子的操作示例如图4所示.每次局部搜索时都需要随机的选择一种算子，这里将Or-Opt算子被选中的概率设置为1/2，2-Opt算子被选中的概率则也为1/2.

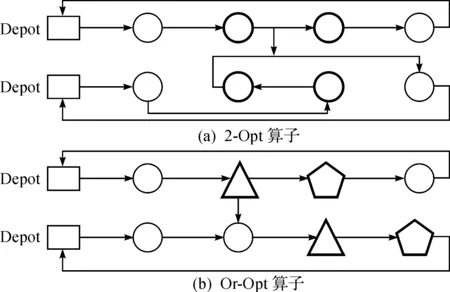
图4 单路径局部优化算子操作示意图Fig.4 Single-path local optimization operator

在Local Search过程中，除了要设计操作算子以外，还要设计算法的局部搜索策略.搜索策略有两种主要的方式[9]：first-improvement和best-improvement.一般情况下，后者的搜索时间会比前者要短，但是前者的求解质量会比较好.经过前期测试，权衡算法求解时间和求解质量之间的关系，这里采用best-improvement策略.

2.6 较差解接受原则和终止准则

较差解接受原则的设计是为了提高算法对求解空间的一个扰动程度，即在局部搜索过程结束后，可以以一定条件接受较差解，以改善算法过早陷入局部最优的缺陷.这里将通过Chiang等[10]提出的模拟退火算法来设计变邻域搜索算法的较差解接受原则，使得算法能在一定概率下接受较差解.模拟退火算法中需要设计温度参数T和每个温度下迭代的次数IT，设初始状态T=T0，完成一个内循环，则T每次减少T0(IT/Imax).

为了防止算法运行时间过长，将引用改编CHEN Qingfeng等[11]设计的终止准则.终止准则分为2个部分：首先，设计VNS算法的最大循环次数为1 000次；其次，如果计算机运行时间超过1 800 s，则程序终止.

3 算法检验

为了检验改进变邻域搜索算法的有效性，需要设计拉格朗日松弛法求解出原问题的一个下界；同时还需要设计具体的算例，并通过改进变邻域搜索算法求得的最优解与下界的差值进行比较分析，以此来评价所设计变邻域搜索算法的有效性.所选算例是在Cordeau标准算例的基础上，针对考虑商品供给价格的多车场车辆路径问题的特殊性作出相应修改的计算算例.

3.1 拉格朗日松弛问题

拉格朗日松弛法[12]是通过将约束规划中造成问题难解的约束吸收到目标函数中，使得问题变得容易求解的一种技术.拉格朗日松弛法可吸收的约束包括3种类型：等式约束、不等式约束和混合型约束.

通过放松原问题的“每个客户点仅接受一辆车的一次配送”约束条件式(4～6)，利用拉格朗日松弛法法求得松弛问题，建立松弛问题模型，分解拉格朗日松弛问题，建立子问题，采用改进的标号法[12]来求解带容量约束的子问题，最后用次梯度法[13]解拉格朗日乘子问题，并得到拉格朗日松弛问题的下界.

3.2 算例验证

试验部分采用20个Cordeau标准算例的前六个算例进行测试，这6个算例的Depot点数都为4.研究并没有涉及超过4个Depot点的中大规模问题，主要是因为在拉格朗日松弛问题中设计了回溯的过程，导致中大规模的算例很难在较短的时间范围内得到松弛问题的下界.变邻域搜索算法和拉格朗日松弛算法的代码使用Matlab编写，算例代码在个人计算机上运行，运行环境为Intel core i3 AMD2.10 GHz，2 GB RAM.

3.2.1 参数设置

在前期试验中，经过对算例的多次试验，以确定算法中的各个参数，以便设计的变邻域搜索算法在其他算例中能够获得较好的最优值.变邻搜索算法中部分重要参数值如下：算法总的迭代次数为1 000次；局部搜索次数为200次；评价函数中车辆超载的惩罚系数E值为200；抖动过程中反转算子的选择概率picross设为0.2；局部搜索过程中的Or-Opt操作算子的选择概率pOr-Opt设为0.5；4个Depot点的单位供给价格分别为7,8,9,10；车辆的最大容量180；车辆单位距离运输成本为6.

3.2.2 算例结果与分析

为了验证所设计的改进变邻域搜索算法对求解所提出问题的有效性，需要对算例的求解结果与拉格朗日松弛算法的求解结果进行比较，表2给出了拉格朗日松弛方法和变邻域搜索算法针对Cordeau的6个算例得到的最优解，以及它们所得结果之间的GAP值，其中GAP=(Z2-Z1)/Z2×100.从表2中可以清晰看出：变邻域搜索算法得到的目标值与拉格朗日松弛下界的差值比值最大时为4.21%，表示与最优目标值比较接近，因此所设计的变邻域搜索算法在中小规模的问题上可以获得较好的值.

表2 拉格朗日松弛&变邻域搜索计算结果对比

图5 最优路径图Fig.5 Optimal path diagram

图5中的两张图都是算例01经过设计的改进变邻域搜索算法获得的最优路径图，惟一不一样的地方是图5(a)中各Depot点的商品供给价格相同，而图5(b)中各Depot点的商品供给价格不同.通过对比这两张图可以看出各个配送中心补给成本的差异给车辆路径规划所带来的影响.相对于商品供给价格相同的图5(a，b)中供给价格高的A-Depot点服务的客户相对变少了，而供给价格低的D-Depot点则服务了更多的客户点.由此可以看出改进的变邻域搜索算法对考虑商品供给价格的多车场车辆路径问题的求解是有效的，并且更加符合实际的车辆运输问题.

4 结 论

针对石油、烟草和食品等多点分布式生产销售配送行业商品供给价格不同问题，在车辆调度问题中综合考虑了供给成本和运输成本，使得成本最小化，提出了考虑商品供给价格的多车场路径问题(MDVRP)，研究目的是使货物供给成本与配送成本的总和最小.建立了考虑商品补给价格的多车场车辆路径问题模型，该问题模型更加符合实际；设计了改进的变邻域搜索算法，在算法的Shaking过程中，设计了8中邻域结构来扩大解的搜索范围，并且同时采用了插入操作算子和交换操作算了，减少了算法陷入局部最优的可能性，在Local Search过程中采用了2-Opt算子和Or-Opt算子，较好的平衡了求解质量和求解时间之间的关系；通过计算算例来验证变邻域搜索算法求解的有效性.研究对于多点分布式生产销售配送行业具有很好的应用前景.

[1] DANTZIG G B，RAMSER J H. The truck dispatching problem[J]. Management science，1959，6(1)：80-91.

[2] GOLDEN B L，MAGNANTI T L，NGUYEN H Q. Implementing vehicle routing algorithms[J]. Networks，1977，7(2)：113-148.

[3] CORDEAU J F，LAPORTE G，MERCIER A. A unified tabu search heuristic for vehicle routing problems with time windows[J]. Journal of the operational research society，2001，52：928-936.

[4] POLACEK M，HARTL R F，DOERNER K，et al. A variable neighborhood search for the multi depot vehicle routing problem with time windows[J]. Journal of heuristics，2004，10(6)：613-627.

[5] 赵燕伟，李文，张景玲，等.多车型同时取送货问题的低碳路径研究[J].浙江工业大学学报，2015，43(1)：18-23.

[6] 魏云飞，黄德才.求解非满载车辆调度问题的免疫遗传算法[J].浙江工业大学学报，2005，33(5)：511-515.

[7] 陈晓眯，孟志青，徐杰.基于混合禁忌搜索算法的动态车辆路径研究[J].浙江工业大学学报，2009，37(5)：580-585.

[8] 金盼.混合多目标进化算法在带时间窗车辆路径问题中的应用[D].杭州：浙江工业大学，2013.

[9] 王征，张俊，王旭坪.多车场带时间窗车辆路径问题的变邻域搜索算法[J].中国管理科学，2011(2)：99-109.

[10] CHIANG W C，RUSSELL R A. Simulated annealing metaheuristics for the vehicle routing problem with time windows[J]. Annals of operations research，1996，63(1)：3-27.

[11] CHEN Qingfeng，LI Kunpeng. Model and algorithm for an unpaired pickup and delivery vehicle routing problem with split loads[J]. Transportation research part E，2014，69(1)：218-235.

[12] 刘泳.基于拉格朗日松弛和分支定界算法的3PL运输调度问题[D].武汉：华中科技大学，2011.

[13] 陶继平.基于拉格朗日松弛法的调度算法研究[D].上海：上海交通大学，2014.

(责任编辑：刘 岩)

Model and algorithm for multiple-depot vehicle routing problem with different supply costs

LU Jiansha， HONG Huanlei， CHEN Qingfeng

(Institute of Industrial Engineering， Zhejiang University of Technology， Hangzhou 310014， China)

In some industries, like tobacco, oil and foodstuff, the supply costs can be different due to the different production costs. So in order to obtain an optimal total cost of delivery and supply, we address the multiple-depot vehicle routing problem (MDVRP) with different supply costs. A multiple-depot vehicle routing model is built considering different production costs; In order to solve the mathematical model, an initial solution based on the nature and characteristics of the problem is generated, and the modified variable neighborhood search algorithm (VNS) by combining eight neighborhoods and local improvement method is designed; Finally, an example was given to test the model and algorithm, and the results prove the method is effective.

supply costs; MDVRP; VNS

2016-03-05

浙江省自然科学基金资助项目((LY15G010009))

鲁建厦(1963—)，男，浙江余姚人，教授，博士生导师，研究方向为精益生产、生产调度和制造业信息化，E-mail：ljs@zjut.edu.cn.

TP301

A

1006-4303(2016)05-0553-06