平面八节点有限元网格生成的位移向量法

蒲军平,汪士应,陈 轶

(1.浙江工业大学 建筑工程学院,浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014；3. 浙江中浩应用工程研究院有限公司，浙江 杭州 310011)



平面八节点有限元网格生成的位移向量法

蒲军平1，2,汪士应1,陈 轶3

(1.浙江工业大学 建筑工程学院,浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014；3. 浙江中浩应用工程研究院有限公司，浙江 杭州 310011)

在曲边图形的有限元计算中，为了保证计算精度及减小计算规模，提出了一种生成八节点四边形单元的位移向量法，以比例渐变的方式综合考虑了四边形各曲边的格栅点对中间各对应点的影响.为了避免出现奇异性单元，在划分的过程中灵活地应用了比例划分.利用开发的VB和FORTRAN程序对一些模型进行了前处理网格划分和有限元数值计算，结果表明：该方法能简单、快速地生成有限元网格，并且数值结果与解析解良好吻合.

曲边四边形；有限元网格；位移向量；比例划分

有限元网格生成是数值计算的前提，从简单的等份划分到自适应网格的划分技术已经能解决各种形状的前处理[1-5].从有限元的前处理到后处理，网格划分的好坏直接决定了计算的速度和精度.笔者提出了一种生成平面八节点四边形单元的位移向量法，将网格生成分为直边单元和曲边单元，为了避免出现奇异性单元在划分的过程中灵活地应用了比例划分[6]，对关键性的局部区域网格可灵活地进行加密.对于曲边单元在使用比例划分的基础上采用位移向量法进行划分，该方法使用简单，通过对一些模型网格划分和计算，精度满足实际要求.

1 直边八节点等参单元的网格生成

如图1所示的直边四边形，四条边的编号分别为1，2，3，4，四个角点分别为A11(x11，y11)，A21(x21，y21)，A31(x31，y31)，A41(x41，y41)，其中1，3边划分份数为n1，2，4边的划分份数为n2.各边上划分点的坐标按下式求得

(1)

其中：n=1,3时，ni=n1,m=1,2,…,n1+1;n=2,4时，ni=n2,m=1,2,…,n2+1.当n1=n2=5时，等份划分网格示意图如图1所示.

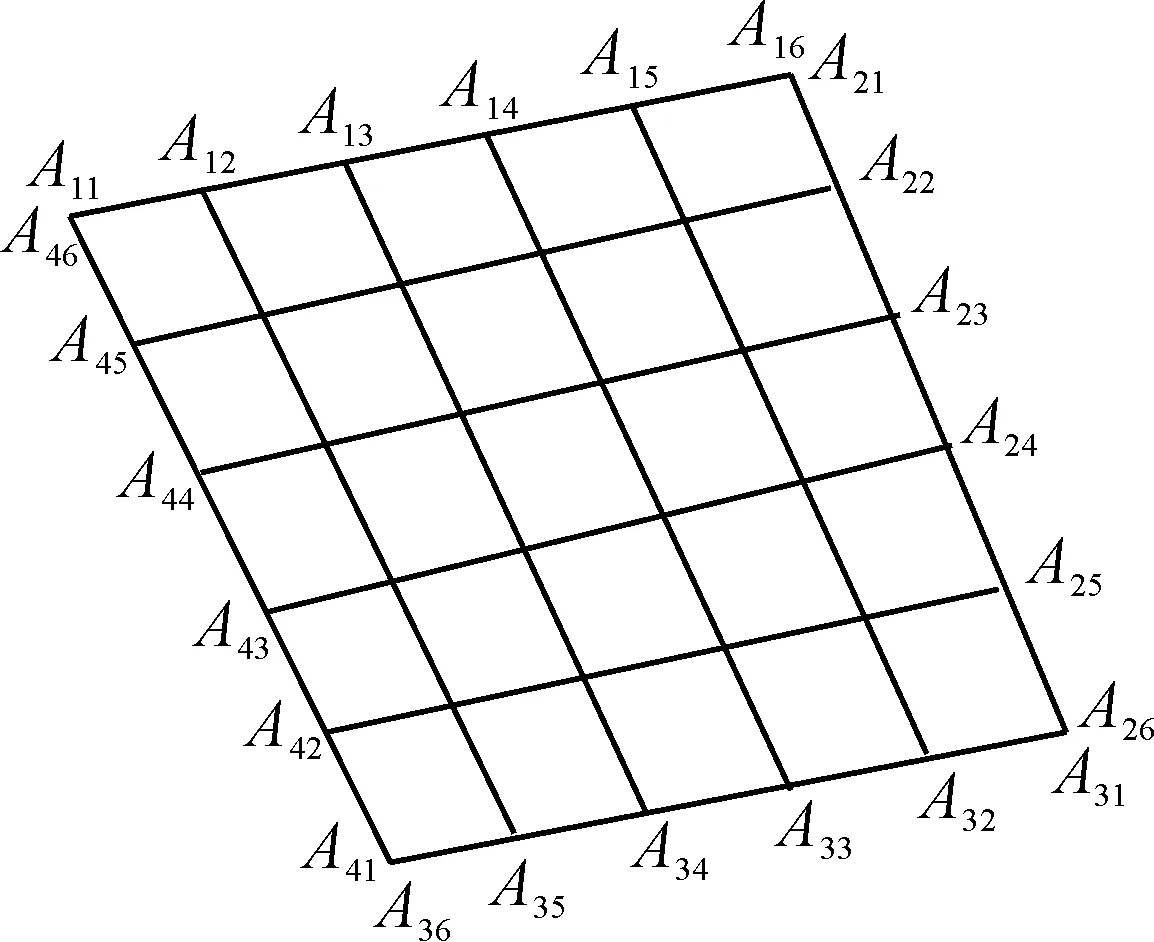
图1 等份划分直边四边形网格Fig.1 Equal parts straight quadrilateral meshes

在对一些图形进行网格划分时，一些关键的局部区域需要网格加密，而大部分区域的网格可划分的较为稀疏，这时需要对每条边加入比例系数，就可以降低有限元网格的数目，在保证有限元计算精度的前提下提高计算效率.

对于比例系数变化下的网格划分同样采用图1的四边形，为了说明方便划分份数同样取为n1=5,n2=5.若需要使角点A11附近的网格加密，使1～4条边的比例系数分别为R1=0.8，R2=1，R3=1，R4=1.2.比例系数是按线段前进的方向，前一段线段始末点x坐标差比上后一段线段始末点x坐标的差，或前一段线段始末点y坐标的差比上后一段线段始末点y坐标的差的比值.前进方向为A11→A21→A31→A41，即

Rm=(ymn-ym(n-1))/(ym(n-1)-ym(n-2))=

(xmn-xm(n-1))/(xm(n-1)-xm(n-2))

m=1,2,3,4;n=3,4,…,n1+1

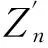
m=1,2,…,n1+1;l=1,2,…,m

(3)

由式(1,3)可得各个线段上其他点的坐标为

n=1,2,3,4;m=2,3,…,n1+1

(4)然后将对边各对应点连线，得到有限元网格划分图形如图2所示.从图2中可以看出：若划分的份数加大，则得到在角点A11附近的网格的加密程度会更高.

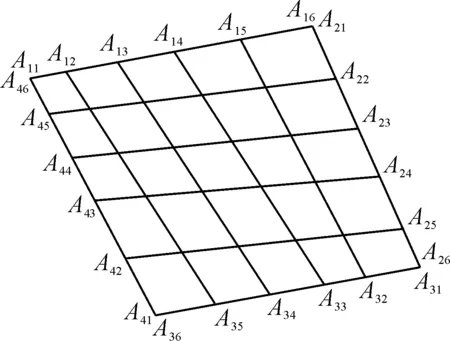
图2 各边比例系数不等时的网格划分Fig.2 Mesh generation with unequal ratio coefficients

2 圆弧曲边八节点等参单元的网格生成

由于曲边单元的线段非线性，为了得到合理的有限元网格，在直边单元的基础上，采用位移向量法对曲边单元进行划分.

对于如图3所示的以圆弧边为主的曲边单元，各边编号分别为1，2，3，4，四个角点坐标分别为A11(x11，y11)，A21(x21，y21)，A31(x31，y31)，A41(x41，y41)，这里为了说明方便同样取1，3边的划分份数为n1和2，4边的划分份数n2均为5，各边的圆心坐标分别为O1(x1,y1)，O2(x2,y2)，O3(x3,y3)，O4(x4,y4)，各种角度计算式为

n=1,2,3,4

(5)其中：αn为各边起始点与圆心的连线与x轴正向的夹角；βn为各边末点与圆心的连线与x轴正向的夹角；θn为各边起始点与末点直角的圆心角的大小.因此，对于圆弧边按比例划分是对所夹圆心角按比例划分.

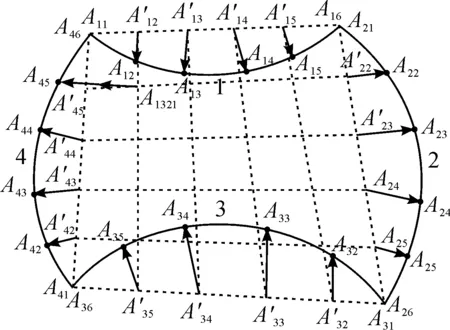
图3 曲边单元等比例划分网格图Fig.3 Dividing grid graph with the same ratio in the curved edge element

当圆弧边是等份划分时，此时对圆心角进行等分即可，由此可得各圆弧边上的划分点的坐标为

n=1,2,3,4;m=1,2,…,n1-1

(6)

其中r为圆弧边的半径.

对于中间点的求取，采用位移向量法.对于每个圆弧边，可以先分别将各圆弧边的首尾进行连接，这样就得到分别以圆弧各角点相连的一个直边单元，如图3中虚线所示，对于靠近每条圆弧边的第一条直边，可以认为是将此直线进行拉伸将直线拉到圆弧边所在的位置，这样以后每条边都可以认为会受到次圆弧边的影响，当随着离圆弧边越来越远时，认为受到的影响越来越小，这样综合起来看，中间网格上的点会受到四边形四条边上对应点的影响，当对四边形四条边循环一次，可以得到个中间点的最终坐标.

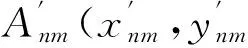
n=1,2,3,4;m=2,3,…,n1

(7)

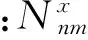
对于中间各点的坐标，需要综合考虑四条曲边对应点的位移向量的影响，越靠近中间点的圆弧边对该点的影响越大.在虚线中所示单元为直边单元，以任意一条边为起点，中间点的坐标都是固定的，下面以第一条边为例，说明如何求得中间点的坐标.

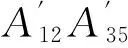
当圆弧向内凹时，此时中间点的坐标改变值为所在直线首末点对应的位移向量的坐标值乘以一个折减系数，方向按照位移向量的方向，折减系数按比例改变，由式(7)并通过程序语句累加可得

(8)

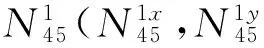
(9)

同理，通过程序语句累加可得各中间点的坐标为

m=2,3，…,n1;n=1,2，…,n2-1

(10)

按照式(10)得出图3的最终网格划分图，如图4所示.

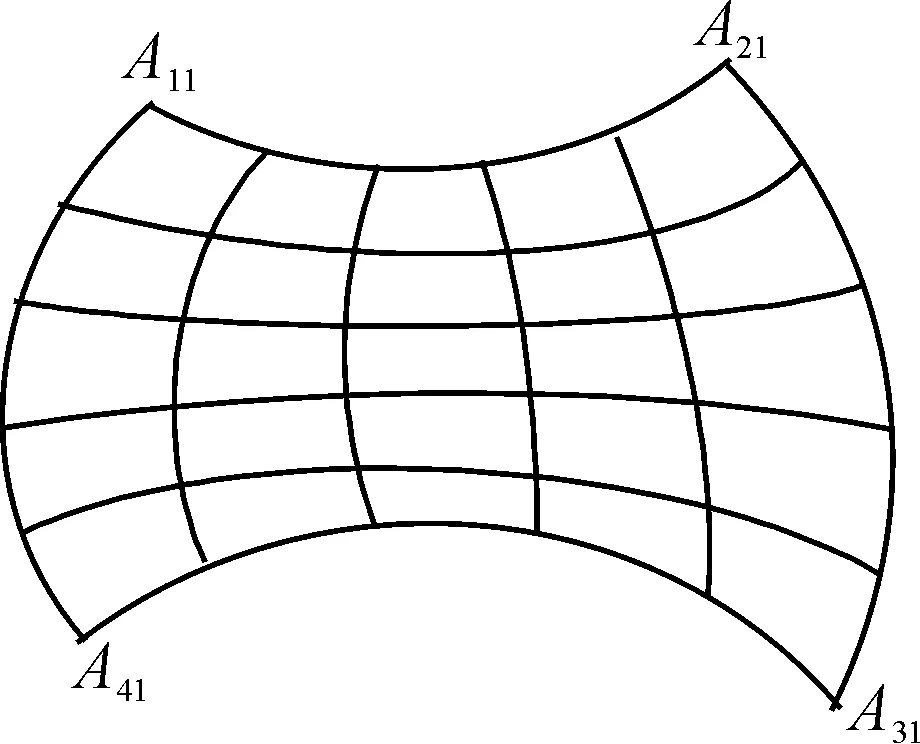
图4 圆弧曲边单元网格划分Fig.4 The meshing of circular arc curved edge elements

对于圆弧边，当需要按照比例划分时，此时的比例系数是按照圆心夹角进行划分，圆弧边上划分点的坐标为

n=1,2,3,4;m=1,2,…,n1-1

(11)

各中间点的坐标仍由式(10)得到.

3 有限元模型网格生成及计算

按以上给出的方法，对一些具体案例进行了网格划分，利用开发的VB系统软件对下述模型进行了前处理网格划分并应用开发的FORTRAN程序进行了数值计算.

算例1 带有裂缝平面板边长分别为2H和2W，裂缝半宽a=100 mm，H/a=L/a=10，竖向拉应力σ0=100 N/mm2，泊松比v=0.3，弹性模量E=2×105N/mm2.生成平面八节点等参元有限元计算模型如图5所示，计算所得裂尖处应力强度因子[8-12]为KI/KI0=0.78.

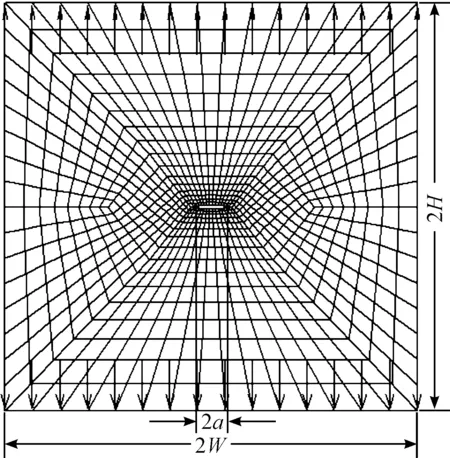
图5 带裂缝平面单元网格划分图Fig.5 The plane mesh graph with a crack

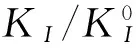
图6 开圆孔的带裂缝平面单元的网格生成Fig.6 Mesh generation with cracks in a plane element with four circular holes

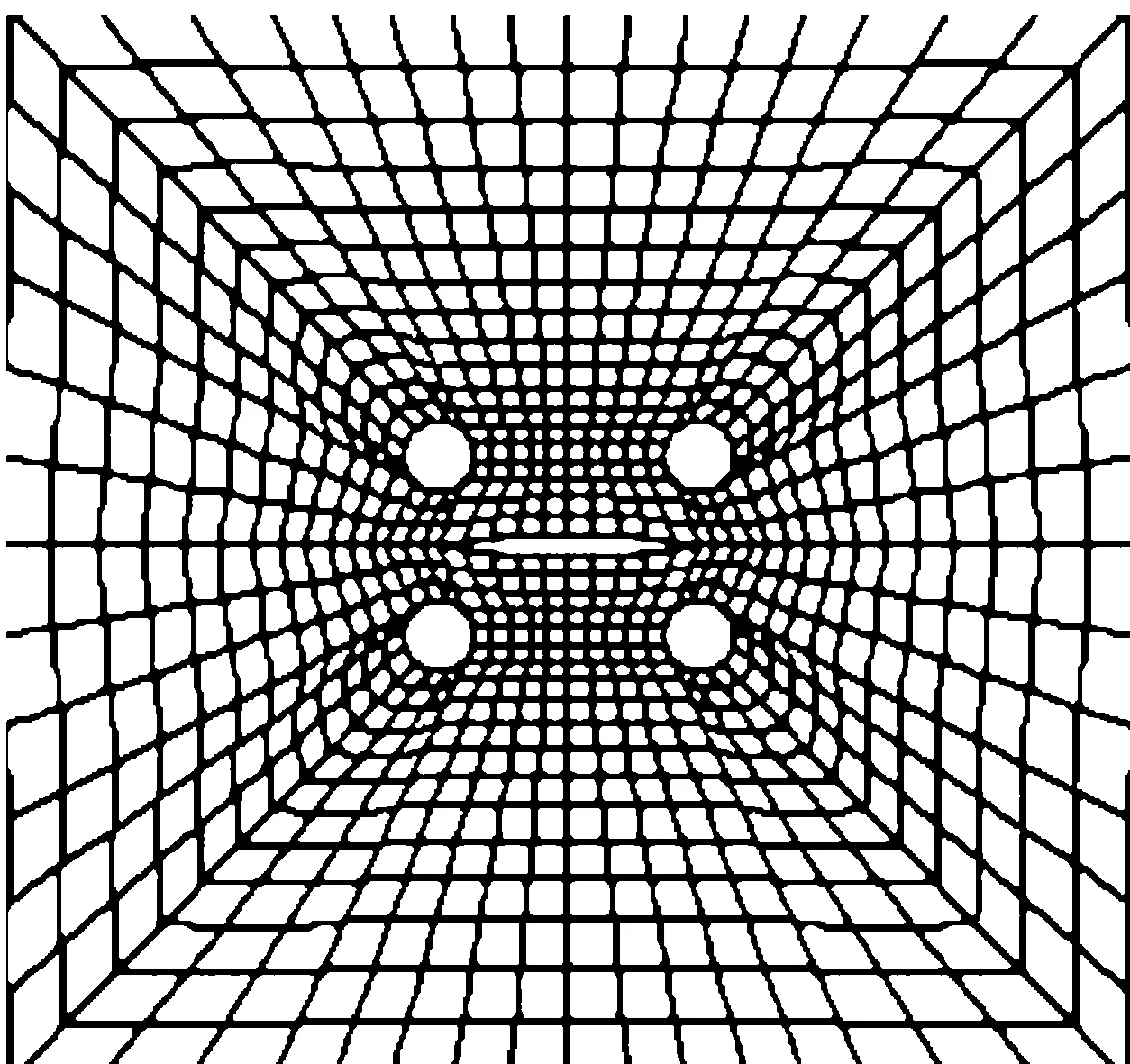
图7 裂缝处的局部放大图Fig.7 Local magnification in the location of a crack

通过对计算结果与解析解进行比较，可看出计算精度满足实际要求.算例1中单元数取为864，节点数为2 684，算例2单元数取1 276，节点数为3 948，算例2较算例1虽然图形更复杂，但由于采用第2节中所述的方法，其规模的增加是可控的，而且这种方法对于更复杂图形处理的效果将更为明显.

4 结 论

曲边平面图形的有限元计算中，通过对圆弧两边的圆心角进行比例划分来对圆弧边划分，可以得到合理的有限元网格.在给出的两个算例模型中，将板上下边缘处的平均荷载转化为集中荷载加在了网格的角点上，由于计算中采用的是八节点等参元，在每两个角点之间还有一个中间点，因此，当荷载以每个中间点进行平均时，荷载将更接近均布荷载，计算的精度也将会更高.笔者给出的方法是针对圆弧曲边进行的网格划分，从该方法中可以看出：当曲边不是圆弧边时，只要该曲边可以用函数进行模拟，按照此方法在曲边前进的方向上，根据曲线的性质灵活地划分格栅点，同样可以得到合理的有限元网格.

[1] 关振群,宋超,顾元宪.有限元网格生成方法研究的新进展[J].计算机辅助设计与图形学学报,2003,15(1):1-14.

[2] HU Jiangchun, WANG Hongfang, HE Manchao. Research finite element method mesh generation based on material-discontinuous-nature[J].Advanced materials research,2011,156/157:74-78

[3] 蒲军平,姚宇龙.平面有限元网格实用划分方法研究[J].浙江工业大学学报,2012,40(1):88-91.

[4] 曾卓,陈家新.扫掠法有限元网格生成方法[J].计算机工程与应用,2013,49(2):219-221.[5] KOKO J. A matlab mesh generator for the two-dimensional finite element method[J].Applied mathematics and computation,2014,250:650-664.

[6] 梁国平.变网格的有限元法[J].计算数学,1985(4):377-384.

[7] 董秀山,刘润涛.判断点与简单多边形位置关系的新算法[J].计算机工程与应用,2009,45(2):185-186.

[8] MAWATARI T,NELSON D V.Method for efficient computation of stress intensity factors from weight functions by singular point elimination[J].Engineering fracture mechanics,2011,78(16):2713-2730.

[9] CAI Gangyi,ZHANG Shixing.Finite element analysis and calculation in cracks of stress intensity factor of thick walled cylinder[J].Advanced mechanical engineering,2010,26/27/28:603-607.

[10] 赵春风,李晓杰,闫鸿浩,等.Ⅰ型裂纹尖端圆弧对应力强度因子影响的数值研究[J].科学技术与工程,2010,10(4):961-965.

[11] MA Youli.Mode I and mode II stress intensity factors based on crack opening and sliding displacements[J].Materials science and engineering,2011,179/180:1417-1422.

[12] 陈炜,庄顺胥,王飞飞.工程结构多裂纹应力强度因子分析[J].科技与创新,2014(19):24.

[13] HOSSEINI-TEHRANI P,HOSSEINI-GODARZI A R,TAVANGAR M.Boundary element analysis of stress intensity factor K-I in some two-dimensional dynamic thermoelastic problems[J].Engineering analysis with boundary elements,2005,29(3):232-240.

[14] PU Junping. Effect of defective holes on crack using the boundary element method[J].Engineering analysis with boundary elements,2006,7(30):577-581.

[15] 刘宝良,邹广平,闫相桥.拉伸载荷作用下单边缺陷-边裂纹应力强度因子研究[J].计算力学学报,2015,32(1):83-88.

(责任编辑：刘 岩)

A displacement vector method for generating planar eight-node finite element mesh

PU Junping1,2, WANG Shiying1, CHEN Yi3

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China; 2.Zhejiang Key Laboratory of Civil Engineering Structures & Disaster Prevention and Mitigation Technology, Hangzhou 310014, China;3.Zhejiang Zhonghao Applied Engineering Technology Institute Co., Ltd., Hangzhou 310011, China)

In the finite element calculation for a geometry with curved edges, a displacement vector method is proposed for generating an eight-node quadrilateral mesh to ensure the computational accuracy and to reduce the amount of computation. In this method, the effect of the grid points on each curved edge on the middle ones on the edge is considered with a gradually changing proportion. To avoid any singular element, the proportional division is flexibly used in the process of mesh generation. With the developed VB and FORTRAN programs, pre-processing mesh generations and finite element computations are conducted for some models. The results show that the finite element mesh can be simply and rapidly generated with this method and that the numerical results are in good agreement with the analytical solution.

curved quadrilateral; finite element mesh; displacement vector; proportional division

2016-01-18

蒲军平(1962—),男，新疆乌鲁木齐人，教授，博士，主要从事固体力学和结构工程研究，E-mail:pjp@zjut.edu.cn.

TP391.7

A

1006-4303(2016)05-0529-04