基于改进智能水滴算法的双资源约束车间调度
陈呈频,赵丹青,董巧英
(浙江工业大学 机械工程学院,浙江 杭州 310014)
基于改进智能水滴算法的双资源约束车间调度
陈呈频,赵丹青,董巧英
(浙江工业大学 机械工程学院,浙江 杭州 310014)
为了解决多资源约束下的作业车间调度问题,提出了一种改进智能水滴算法.该算法采用了基于工序与加工机器相融合的两层编码方式建立问题和算法的映射关系,运用随机方法初始化产生可行解,结合精英保留策略加快算法的收敛速度,嵌入迭代局部搜索算法以增强算法的全局搜索能力,并来解决影响车间调度的3个主要成本因素,即最小化延期成本、最小化人工成本和最小化设备运行成本.通过实例的收敛性能对比,证明算法具有优秀的全局开发能力和收敛性.实验表明了该算法能够有效求解双资源约束车间调度问题.
改进智能水滴算法;多目标调度;作业车间;迭代局部搜索
生产调度一直以来是制造企业面临的一个基础且重要的问题,随着市场经济的发展,客户需求日趋多样化、个性化,企业需要以更快更高效的生产效率去满足市场的变化.由于需求的多样化使得生产调度趋于复杂,一种快速有效的作业车间调度方法成为急需解决的科学问题.
作业车间调度是在制造企业资源有限的约束条件下,为达到一个或者多个不同的目标而对资源进行合理配置的过程[1-2].在实际生产中车间调度往往受到多种加工资源的约束,如设备、操作人员、原材料及其他辅助生产工具等[3].刘志刚等[4]针对非等同并行机生产车间,在设备约束的基础上采用免疫算法进行问题求解,但所用的方法由于具有记忆性比较容易早熟,对模型目标的设计也过于单一,未对生产成本等因素加以考虑.张其亮等[5]针对存在的阻塞限制工件又存在无等待约束工件的柔性车间提出了离散粒子群优化算法,但提出方法难以满足实际的调度需求.张超勇等[6-8]采用多目标车间调度运用不同的智能优化算法进行了多元化研究,在满足约束条件的前提下调度质量得到了显著的提高,但未对设备运行情况进行分析,在调度模型中仅考虑设备约束而欠缺对人力约束等其他制造资源的考虑.分析现有研究发现车间调度大多是仅考虑设备约束,随着劳动力成本的不断攀升,员工效率成为企业发展硬瓶颈,许多企业开始重视员工效率的提升,因此需要结合人力约束和设备约束对车间进行调度,同时将设备运行成本、人力成本和完工时间等目标加入调度模型中,使建立的模型更加符合实践中的作业车间调度环境.群智能算法不断发展,出现了智能水滴算法[9-10],目前该算法在TSP[11]、路径规划问题[12]应用取得了不错的效果,具有优秀的全局搜索能力,在调度领域的研究仅限于流水线调度[13]和供应链优化上.为此,在基本智能水滴算法基础上进行改进,提出了适合求解车间调度问题的改进智能水滴算法.
1 调度问题描述
作业车间调度一直以来是NP难问题,多重资源约束下的作业车间调度更是难上加难,需要考虑多因素,满足多约束.加工能力、制造工期、加工成本和人员安排等多因素的全面分析更能保证调度的可行性.作业车间调度问题可以表述如下:有n个代加工的工件在m台设备上加工,每一个工件Ji包含ni道工序Oi,j(j=1,2,…,ni),所有工件的工序都必须按照已定的工艺顺序进行产品加工.每道工序Oi,j能在一个或者若干个设备上进行加工,不同设备对同一个产品的加工时间存在不同.作业车间有w名多能工,每名员工掌握多台设备的操作技术.车间生产能力除了受加工设备影响外,还会受到人力资源的影响,当工序达到设备时所需的人员不一定处于可用状态.调度的目的是在设备和人力双重约束条件下合理安排每台设备上的工件加工顺序.
调度目标有多个,其分别为最小化最大完工时间、最小加工成本和最小化机器运行成本.其需要满足以下的约束:
1)每个工件在设备上处理时不允许被中断,必须直到完工,不得中途停止插入其他工件.
2)每台设备只能同时处理一个工件.
3)允许工序间存在等待状态、设备闲置情况.
4)工件无优先级限制.
5)生产过程中的运输时间不予考虑.
6)设备在生产时间内可完全运行,不考虑故障情况.
7)每个订单只包含一种产品,产品加工工艺确定.
2 目标函数设计
多资源约束下的作业车间调度从一个更为全面和合理的角度来安排其计划的制定,从而实现在一定产能的基础下低成本高效率的生产理念,模型考虑最小化最大完工时间、最小人工成本、最小设备运行成本3个优化目标,针对这3个目标建立目标函数以及相关约束.
2.1 最小化延期成本
作业车间在每个产品安排过程中会有产品加工的先后顺序,n个工件在m台设备存在不少可行的调度方案.由于不同的方案的最大完工时间会存在较大差异,由此造成的订单延期情况等会影响企业的盈利,所以把最小化延期成本作为目标函数进行考虑,其目标函数f1为
(1)
其中:Ci为第i个工件最后一道工序的完成时间;di为第i个工件的截至交货时间;A为单位延期成本.
2.2 最小化人工成本
在劳动力成本较之前普遍偏高的情况下,员工的劳动时间利用率应该尽可能地提高,对于调度方案的人工成本的限制可以让企业能获取更大的盈利空间,另一方面从员工工作时间的减少上入手可以避免人员冗余.其目标函数f2为
(2)
其中:B为单位人工成本;Pi,j,k为i工件的j工序在k设备上的加工时间;Xi,j,k为0-1函数,取值为1时表示i工件的j工序在k设备进行加工;Dk为k设备需要的操作员工数量.
2.3 最小化设备运行成本
因为不同工序存在多个备选加工设备,每个设备对同一工件的加工时间也会有所差异,而不同设备会因设备新旧程度、类型和能耗程度的不同导致开工后实际运行的单位成本存在一定差异,所以设备的运行成本也需要加以考虑,其目标函数f3为
(3)
其中:Ek为为设备k单位运行成本.
综上所述,结合企业对于不同目标的重要程度不同,模型的表达式为
F=μ1f1+μ2f2+μ3f3
(4)
限制条件分别为
(5)
Pi,j,k+Si,j,k≤Si,j+1,k′
(6)
Si′,j′,k-Pi,j,k≥Si,j,k
Yi,j,k/i′,j′,k=1,Xi,j,k=1,Xi′,j′,k=1
(7)
其中:式(5)表示工件的某工序只能在一台设备上加工;式(6)表示同一工件的工序前后关系;式(7)表示一台设备同时只能加工一个工件的一个工序;Si,j,k为产品i的j工序在k设备上加工的结束时间;Yi,j,k/i′,j′,k为k设备上产品i的j工序优先于且相邻与产品i′的j′工序加工.
3 改进的智能水滴算法
智能水滴算法是模拟自然界中的水滴的运动并寻找最佳路径而形成的一个算法[11]原始的智能水滴算法在求解过程中往往收敛较慢,时常会陷入局部最优的处境,为了避免这种情况的出项,由此加入了精英策略,同时与迭代局部域搜索算法结合提高其收敛速度.此外,将遗传算法的变异操作嵌入其中来有效的保证算法在寻优过程中跳出局部最优,避免陷入早熟.
3.1 算法流程
Step 1 参数初始化,包括初始化水滴个数N,最大迭代次数Tmax,静态参数av,bv,cv,as,bs,cs,智能水滴初始速度v0,初始所携带的泥土量s0.
Step 2 产生初始位置列表,将初始智能水滴置于该位置.
Step 3 依据位置列表逐个计算水滴的适应度值,记录并更新适应度以及其对应的排序.
Step 4 计算每个IWD从当前位置i移动到符合领域范围的下一位置j的概率p(i,j,IWD).
Step 5 用轮盘赌选择策略选取合适的下一位置jbest,然后更新IWD的位置列表.
Step 6 对于每一个IWD从当前位置i到下一位置jbest,计算并更新其速度和泥土量.
Step 7 对每一水滴重复步骤3~6直至N个智能水滴均得到更新.
Step 8 依据模型的多个目标函数评价所有IWD更新后的质量FIWD.
Step 9 从所有解FIWD计算出迭代最优解F.
Step 11 将迭代次数加1,如果迭代次数小于Tmax,则回到步骤3.
Step 12 结束算法,输出最优解Fbest.
具体的算法流程如图1所示.

图1 IIWD算法流程Fig.1 IIWD algorithm process
3.2 算法的具体设计
1) 编 码
与遗传算法等进化算法类似,在实际求解问题中需要建立智能水滴与调度问题之间的映射关系,每个智能水滴的位置代表的是一种可能的调度方案,采用陈勇等[14]提出的编码方式,基于工序与加工机器相融合的编码方式,在此基础上增加一层编码,代表人力指派.每条编码都采用m×3阶矩阵表示,即
(8)
其中:第1行为工件号;第2行为设备选项;第3行为人员编号.每一列为一个工序的调度,式(8)中第一列的1,3,2,表示工件1的第1道工序在第3个设备选项所对应的设备上由第2个员工进行加工生产.
2.3 “三线耦合”的新型职业农民培养路径 采取高职院校定向委托培养、农民社区学院开放培育、田间课堂专项培训3条相互交融渗透的培养路径,有效促进高职教育与农业产业之间的深度融合,将教育办到生产一线。采用“政校合作、定向招生、订制课程、定岗培养、定向就业”培养方式,创办了全国高职院校首家“青年职业农民定向培养班”;按照“产教衔接、开放共享、终身学习”的培养理念,搭建了农民社区学院培养平台,创新了新型职业农民培养载体;采用“农民点菜、专家下厨”的互动教学,创新了新型职业农民培养的田间课堂教学方式,为地方经济发展培养了一大批懂技术、善经营、会管理、下得去、用得上、留得住的本土化高素质新型职业农民。
2)初始化
采用随机编码的方式产生初始解,按照模型的约束条件对初始解进行修正,保证其为可行解.
3)下一位置的选择
采用轮盘赌的方式对每个IWD的概率进行选择从而提高全局搜索能力,同时可以避免过早陷入局部最优,其概率计算公式为
(9)
(10)
(11)
其中:式(10)中εs为很小的正数,避免函数f分母为零;式(11)中函数g则是为了保证位置i,j之间的变量s(i,j)为非负值,s(i,j)表示从位置i到位置j中的路径泥土含量.在模型求解中,路径中泥土含量与模型目标函数值存在正比关系,目标函数越大,则泥土量越大,被选中的概率越小.
4)精英策略
对于每次迭代后的智能水滴群体,采用精英保留策略,具体的做法是保留上一次迭代的最优水滴,取代本次迭代的最差水滴.采用这种策略可以有效的加快算法的收敛速度,解决智能水滴算法收敛慢的现状.
5)迭代局部搜索
每次对每个水滴迭代中,置初始调度解为h0,对搜索距离在d半径内的N个可能的位置hc,分别计算其所对应的适应值,若N个下一位置的搜索值中最优适应值优于初始调度解则替代最优调度解,其伪代码如下:
Generate initial solution h0.
hc←h0.
while (termination condition do not meet) do
hl←Local search(hc).
if q(hl)≤q(hc)then hc←hl
end while
return the best obtained solution hc.
6)迭代进化
在每次迭代过程中需要对每个水滴的位置和其状态(包括速度和水滴携带的泥土量)进行更新,具体进化公式分别为
(12)
(13)
4 案例应用
为了说明改进后的算法的有效性,以某企业的实例作为基准问题进行验证.该企业是一家生产研发物流装备的公司,现选取其皮带机输送机生产的6种部件,不同部件的不同工序可在多台机器上进行加工,目标函数权重以企业具体情况而定,表1为工序加工时间,表2为操作工人掌握设备操作技术情况(Y表示该员工已经掌握该设备操作技术),案例考虑设备约束和员工资源约束.产品到达时间都为0,产品交货时间为:d1=30;d2=25;d3=20;d4=35;d5=30;d6=25.
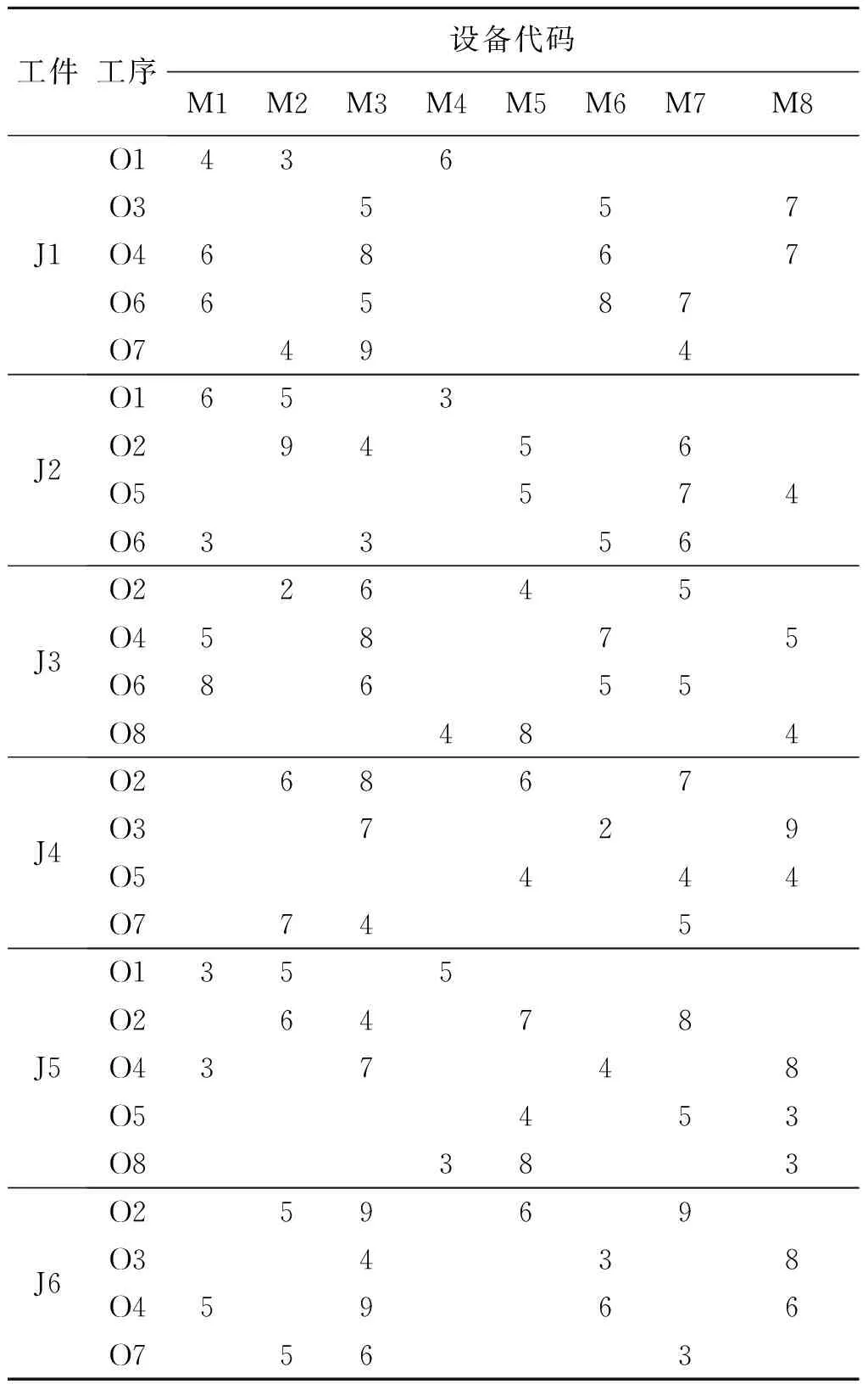
表1 各部件工序加工时间表
表2 员工掌握设备操作技能情况
Table 2 The situation for staffs to master the skills of equipment
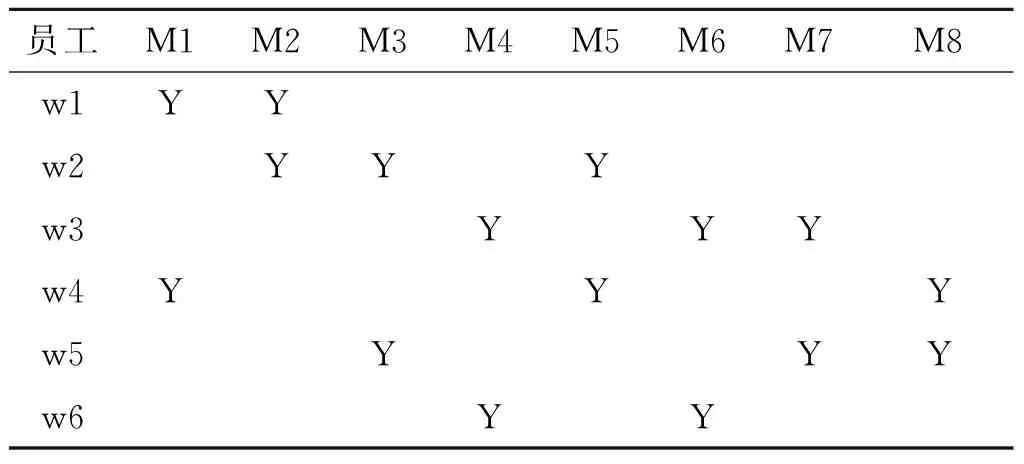
员工M1M2M3M4M5M6M7M8w1YYw2YYYw3YYYw4YYYw5YYYw6YY
案例中的所有工序均只需要一名员工进行加工生产,人工成本计算按工位单人员计算,调度方案对人员和设备的安排的不同会导致人工成本的变化,从而方案的人工成本优劣可以得到比较.
Matlab程序编程的具体参数设置为:av=1,bv=0.01,cv=1,α=1,as=1,bs=0.01,cs=1,θ=1.为了比较改进智能水滴算法(简称IIWD)与其他进化算法的性能,对比GA算法和基本IWD算法进行实验,实验结果如表3和图2所示.在迭代80次内,IIWD,IWD与GA都能搜寻到最优解,IWD的搜寻速度明显慢于IIWD与GA.而GA则由于其早熟的原因运算结果不如其他理想.从图2中可以得出:IIWD的收敛性明显优于IWD,其求解结果明显优于GA.

表3 3种算法测试结果

图2 3种算法收敛性分析Fig.2 Convergence analysis of three algorithm
以上说明IIWD算法在收敛性以及求解结果上都明显优于其他两种算法,这也验证了算法的可行性和有效性,证明IIWD可以有效地应用和解决作业车间的多目标规划调度问题.
对于案例中,图3为收敛后的IIWD得到的调度方案的甘特图,每个矩形框内的数字含义为“工件号-工序号-员工序号”.

图3 IIWD调度甘特图Fig.3 IIWD Schedule Gantt chart
5 结 论
针对多资源约束条件下的调度问题,提出求解作业车间多目标问题的改进智能水滴算法.结果表明:对车间调度问题在设备约束的基础上增加了人力约束;在目标设定上,新增了设备运行成本,同时结合最小化最大完工时间、最小化人工成本进行模型建立,使模型更好反映实际调度情况.采取了一种新的算法求解所建立的模型,该算法在智能水滴算法的基础上结合精英策略和迭代局部搜索算法,能够很好的平衡全局开发能力和收敛性.通过案例对模型和算法进行验证,求解结果表明改进的智能水滴算法在求解多资源约束下的调度能快速寻找到满意的调度方案,对于车间调度优化具有工程指导意义.
[1] 刘爱军,杨育,邢青松,等.柔性作业车间多目标动态调度[J].计算机集成制造系统,2011,17(12):2629-2637.
[2] GLATARD T,CAMARASU S. A model of pilot-job resource provisioning on production grids[J].International journal of computer integrated manufacturing,2012,25(1):3-10.
[3] 何桂霞.特殊工艺约束下最小完工时间并行多机调度问题的研究[J].浙江工业大学学报,2010,38(1):63-66.
[4] 刘志刚,李言,李淑娟. 基于蚁群算法的Job-Shop多资源约束车间作业调度[J]. 系统仿真学报,2007(1):216-220.
[5] 张其亮,陈永生. 解决具有混合约束柔性流水车间调度问题的粒子群优化算法[J]. 计算机应用研究,2013(11):3253-3256.
[6] 张超勇,董星,王晓娟,等.基于改进非支配排序遗传算法的多目标柔性作业车间调度[J].机械工程学报,2010,46(11):156-164.
[7] SCHAFFER J D. Multiple objective optimization with vector evaluated genetic algorithm[C]//. International Conference on Genetic Algorithm. New Jersey:Lawrence Erlbaum Associates, 1985:93-100.
[8] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multi-objective genetic algorithms:NSGA-Ⅱ[J].IEEE transactions on evolutionary computation, 2002, 6(2):182-197.
[9] HAMED S H.Problem solving by intelligent water drops[C]//IEEE Congress on Evolutionary Computation. Singapore: IEEE, 2007:3226-3231.
[10] KAMKAR I,AKBARZADEH-T M R,YAGHOOBI M.Intelligent water drops a new optimization algorithm for solving the vehicle routing problem[C]// IEEE International Conference on Systems, Man and Cybernetics. Istanbul:IEEE,2010:4142-4146.
[11] 赵莉,丁海军.智能水滴算法求解TSP问题的研究[J].云南民族大学学报,2015,24(1):62-65.
[12] 周虹,张磊,谭阳.旁域更新智能水滴算法软时间窗车辆路径优化[J].计算机工程与应用,2015,51(20):253-258.
[13] 周季华,叶春明,盛晓华,等.基于智能水滴算法置换流水线调度问题的研究[J].计算机科学,2013,40(9):250-253.
[14] 陈勇,章金红,鲁建厦.基于GA-TS混合算法的多装配线调度建模[J].浙江工业大学学报,2013,41(4):355-359.
(责任编辑:刘 岩)
Dual resource constrained scheduling of job shop based on improved intelligent water drop algorithm
CHEN Chengpin, ZHAO Danqing, DONG Qiaoying
(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)
In order to solve the problem of job shop scheduling with multi resource constraints, an improved water drop algorithm is established. It adopts encoding method of the integration process and processing machine. Also it uses random method to initialize the generation of feasible solutions. Besides, it combines with the elite strategy and iterated local search algorithm. This algorithm is aimed to solve the three main factors: minimizing the delay cost, minimizing the labor cost and minimizing the equipment cost. At last, after comparing the convergence performance, the good global development capability and convergence have been approved. The model and the algorithm are proved to be effective in solving job shop scheduling problem.
improved intelligent water; multi-objective scheduling; job shop; iterated local search
2016-03-11
浙江省自然科学基金资助项目(LQ14E050004)
陈呈频(1963—),男,浙江义乌人,教授,研究方向为生产调度、综合集成系统设计和工业工程等,E-mail:ccp@zjut.edu.cn.
TP181
A
1006-4303(2016)05-0559-05

