地形横向密度扰动对于区域大地水准面建模的影响
吴怿昊 罗志才,2
1 武汉大学测绘学院,武汉市珞喻路129号, 430079 2 地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
地形横向密度扰动对于区域大地水准面建模的影响
吴怿昊1罗志才1,2
1 武汉大学测绘学院,武汉市珞喻路129号, 430079 2 地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
分别利用Helmert和KTH法模拟试算了不同地形起伏区域内横向密度扰动对于大地水准面的影响。结果表明,在地形起伏较小的平原或丘陵地带,横向密度扰动的影响一般不会超过cm级,在精度允许的范围内可以忽略其影响;在地形起伏较大的山区,横向密度扰动的影响可达cm甚至dm级,对于cm级大地水准面精化而言,需要考虑其影响。此外,基于Helmert与KTH法解算的结果在地形起伏剧烈的山区差异较大,由于Helmert法计算地形效应时忽略了外区地形质量的影响,其解算结果可能存在偏差。总体而言,在地形起伏剧烈的山区建模时,需利用多种计算方法基于实测数据分别进行试算,通过计算的变密度大地水准面与实测的GPS水准数据进行比较分析,得到适合该区域的大地水准面建模方法。
地形横向密度扰动;大地水准面;赫尔默特凝聚法;KTH法
确定高精度、高分辨率的大地水准面是物理大地测量的主要任务之一。利用Stokes理论解算大地水准面的前提是大地水准面外部不存在剩余质量,即需对地形质量进行相应的处理,并对实测重力进行归算[1]。对地形质量处理时往往将地壳密度作为常数而不考虑其变化,这一假设不仅在理论上存在不严密性,在实际大地水准面的解算中也可能会引入较大的误差。特别是在地形复杂、起伏大的山区,地壳密度可能偏离平均值10%~20%,横向密度扰动可能会引起较大的误差[2]。
国内外学者对横向密度扰动对大地水准面的影响作了相关研究。文献[2]从理论上证明,即使是一个很小的密度扰动在山区也可能会引起dm级的误差;文献[3]利用赫尔默特凝聚法计算加拿大山区横向密度扰动对大地水准面的影响,表明在该区域横向密度扰动的影响达7.0 cm;文献[4]的研究表明,横向密度扰动对大地水准面的影响在最深湖(贝加尔湖)和最高山脉(喜马拉雅山)分别达到了1.5 cm和1.78 m;文献[5]计算了伊朗山区地壳密度扰动对大地水准面的影响,表明其影响可达dm级或以上。国外学者的研究结果表明,在地形起伏较大的区域及多山地区,横向密度扰动对大地水准面的影响较大,需要谨慎考虑其影响。由于不同的计算方法对于地形质量的处理方式不同,基于不同方法计算的横向密度扰动对于大地水准面的影响也会存在差异。本文利用赫尔默特凝聚法和KTH法,以国内不同区域的大地水准面建模为实例,对比分析地形横向密度扰动对大地水准面的影响,并分析不同建模方法的优劣,以期为后续的山区大地水准面精化提供参考。
1 横向密度扰动影响的计算方法
1.1 赫尔默特凝聚法
赫尔默特凝聚法(Helmert)并不是移除地形质量的影响,而是把地形质量的影响压缩到大地水准面以下,并利用与高程呈简单线性关系的重力梯度将地面重力异常向下延拓到大地水准面上。赫尔默特重力异常ΔgHelmert可表示为[6]:
(1)
式中,Δgfa表示空间重力异常。计算点p的局部地形改正tc可表示为[1]:
(2)

(3)
式中,hp表示点p的地形高,R表示地球的平均半径。
恢复移去地形质量的间接影响,可得到最终的大地水准面。间接影响Nind可表示为[6]:
(4)
式中,γ表示平均正常重力,hp和h表示计算点和流动点的地形高。
联合式(2)及式(3),横向密度扰动Δρ对Helmert重力异常ΔgHelmert的总影响可表示为:
(5)
横向密度扰动对间接影响的影响ΔNind可表示为:
(6)
结合式(5)及式(6),横向密度扰动对大地水准面的总影响ΔNtotal可表示为:
(7)
式中,S(ψ)表示Stokes函数。
1.2 KTH法
KTH法利用随机性改化形式的Stokes公式计算大地水准面。与传统方法相比,KTH法无需进行重力归算,而直接采用地面重力异常计算得到近似的大地水准面高,在此基础上加上大地水准面高的附加改正项得到最终的大地水准面[7-10]。区别于传统方法计算地形质量影响时需要分别计算直接影响和间接影响,该方法直接计算地形质量对大地水准面的总影响,即组合地形影响,可表示为[7,11]:
(8)
(9)
式(9)中等式右边第二项的影响较小,通常可将其忽略不计,此时可表示为:
(10)
我国采用正常高系统,计算的大地水准面往往要转换为似大地水准面,横向密度扰动同样也会影响上述转换结果。大地水准面和似大地水准面差距可表示为:
(11)

(12)
简单布格重力异常ΔgB受到横向密度扰动的影响,造成大地水准面和似大地水准面的差距也会受到地壳密度扰动的影响。经过简单的推导可得,横向密度扰动对大地水准面和似大地水准面差距的影响Δζρ可表示为:
(13)
对比式(10)和式(13)可知,利用KTH法计算横向密度扰动对大地水准面的影响与计算横向密度扰动对大地水准面和似大地水准面差距的影响公式一致,因此在后续的试算中可以利用KTH法计算横向密度扰动对大地水准面的影响,即计算出了横向密度扰动对大地水准面和似大地水准面差距的影响。
2 数值分析
国外学者往往通过地质勘察部门所发布的地质图、地理信息数据及相关信息获取特定区域的真实地壳密度资料[3]。由于在进行相关研究中缺乏相应的地壳密度资料,本文通过模拟研究计算不同区域、不同密度扰动对该区域大地水准面精化的影响,以此说明在这些地区是否要考虑横向密度扰动的影响。本文主要采用普拉特-海福特均衡补偿系统计算的地壳均衡密度扰动[12]和模拟的特定横向密度扰动。普拉特-海福特均衡模型假设大地水准面下方某一深度处存在一个补偿面,该补偿面下方的密度是均匀的,上方的质量在该补偿面上产生的压强处处相等。通过均衡补偿理论就可以得到每个柱体的密度ρ,在不影响精度的情况下通过适当的平面近似ρ可表示为[12]:
(14)
式中,D表示大地水准面到补偿面的距离,即补偿深度;H为地面到大地水准面的距离,即海拔高程;ρ0=2.67g/cm3为平均地壳密度。
通过式(14)可得到近似的地壳密度扰动Δρ:
(15)
为了对比分析不同密度扰动对局部大地水准面精化的影响,本文在试算区域内定义了3种常密度扰动Δρ1、Δρ2及Δρ3,分别偏离平均地壳密度的5%、10%及15%,表示如下:
(16)
式中,ρ1、ρ2及ρ3表示3种相应的地壳密度。
由于密度扰动对大地水准面的影响与密度扰动大小和计算区域的地形起伏相关,为了进一步说明地形起伏的影响,本文选取两个地势高低、地形起伏各异的试算区域:1)我国东南某丘陵区域ΩA,其纬度范围为26°~28°,经度范围为116°~118°,见图1(a);2)我国四川省西部某山区区域ΩB,其纬度范围为31°~33°,经度范围为101°~103°,见图1(b)。DEM模型采用SRTM模型,其分辨率为3″×3″,即90 m×90 m,其相应的统计信息见表 1。由图1、图2可知,区域ΩA地形总体上起伏较小,属于较为平坦的区域。结合表 1和表 2,其高程平均值约为430 m,平均均衡密度扰动为0.028 g/cm3,约为平均地壳密度的1%。区域ΩB属于海拔高程较高的山区,地形总体上起伏较大,该区域高程平均值约为3 885 m,均衡密度扰动的平均值0.236 g/cm3,偏离平均地壳密度约为8.8%,地壳密度扰动较大。

图1 不同区域的数字地形模型Fig.1 The DEM over various computational regions

max/mmin/mmean/mstd/mrms/mΩA215524430.45270.32508.29ΩB613219523885.58467.633913.62
采用均衡密度扰动及特定的3种密度扰动,计算横向密度扰动对大地水准面的影响。利用不同方法计算区域ΩA内横向密度扰动影响的结果如图3和图4所示。由图可见,密度扰动对大地水准面的影响与地形起伏和密度扰动本身的大小有关。由于试算区域总体上较为平坦,真实的地壳密度与平均地壳密度相差不大,横向密度扰动对大地水准面的影响较小。若将均衡密度扰动作为真实的密度扰动信息,从表 3统计信息可知,由不同方法计算的均衡密度扰动引起的大地水准面误差不超过cm级,其标准差在mm量级,在精度允许的范围内可以忽略其影响。由于该计算区域地势较为平缓,地形影响较小,上述两种方法计算的横向密度扰动影响的差异并不显著。
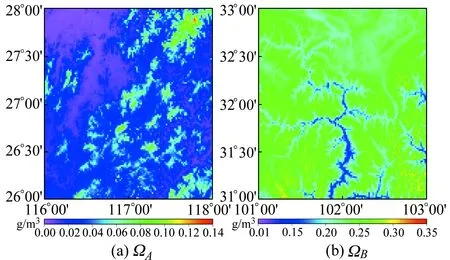
图2 不同区域的地壳均衡密度扰动Fig.2 The variation of isostatic crust density over various regions

max/g·cm-3min/g·cm-3mean/g·cm-3std/g·cm-3rms/g·cm-3ΩA0.1300.0020.0280.0180.033ΩB0.3140.1250.2360.0260.237
区域ΩB内基于不同方法计算的横向密度扰动影响的结果如图5、图6和表 4所示。可以看出,试算区域地形起伏较大,真实的地壳密度与平均地壳密度相差较大,横向密度扰动对大地水准面的影响较大。基于Helmert法计算的均衡密度扰动对其影响的最大值可达9.4 cm,标准差达到2.7 cm(图5)。若真实地壳密度与平均地壳密度相差更大,会引入更大的误差。KTH法的计算结果与地形起伏的相关程度更为明显,基于均衡密度扰动计算的影响的最大值达到dm级,标准差为5.1 cm(图6),其结果对大地水准面有较大影响。Helmert法与KTH法在该区域的解算结果有较大差异(表 4),其主要原因是Helmert法计算密度扰动的直接影响和间接影响时(见式(5)、式(6)),由于积分区域的限制而忽略了外区地形质量的影响(即地形效应的中长波影响),使得基于该方法计算的结果产生偏差,地形起伏越剧烈,可能产生的偏差越大。这一结论与文献[1]的研究结果一致。相比而言,KTH法基于全球高程球谐展开式求解的理论能够较好地顾及地形影响的中长波效应,在实际计算中能更为精确地逼近相应的地形效应。由于本文研究过程中缺乏实测的重力和GPS水准数据,现阶段难以定量给出基于经典Hermert法计算地形效应引入的偏差对于大地水准面的影响,未来基于某山区大地水准面建模的实例分析有望进一步讨论两种方法的差异及建模的优劣性。总体而言,在地形起伏较大的山区,由于横向密度扰动引入的地形效应对高精度的局部重力场建模的影响较大,实际计算中可能需要利用多种计算方法(包括KTH、RTM及Molodensky等方法)基于实测数据分别进行试算,通过计算的变密度大地水准面与实测的GPS水准数据进行比较分析,得到适合该区域的大地水准面建模方法。

图3 利用Helmert法计算的不同横向密度扰动对大地水准面的影响(ΩA)Fig.3 The effect on geoid modeling by using Helmert method based on various crust density variation(ΩA)

图4 利用KTH法计算的不同横向密度扰动对大地水准面的影响(ΩA)Fig.4 The effect on geoid modeling by using KTH method based on various crust density variation(ΩA)

方法密度扰动max/mmin/mmean/mstd/mrms/mHelmert法均衡密度扰动0.0086-0.0002 0.00050.00110.0012地壳密度偏离正常值的5%0.0216 0.0062 0.00140.00150.0021地壳密度偏离正常值的10%0.0432 0.0123 0.00290.00300.0042地壳密度偏离正常值的15%0.0649 0.0185 0.00430.00440.0062KTH法均衡密度扰动0.0000-0.0235-0.00060.00120.0014地壳密度偏离正常值的5%0.0000-0.0240-0.00150.00190.0024地壳密度偏离正常值的10%0.0000-0.0481-0.00290.00390.0049地壳密度偏离正常值的15%0.0000-0.0721-0.00440.00580.0073

图5 利用Helmert法计算的不同横向密度扰动对大地水准面的影响(ΩB)Fig.5 The effect on geoid modeling by using Helmert method based on various crust density variation(ΩB)

图6 利用KTH法计算的不同横向密度扰动对大地水准面的影响(ΩB)Fig.6 The effect on geoid modeling by using KTH method based on various crust density variation(ΩB)
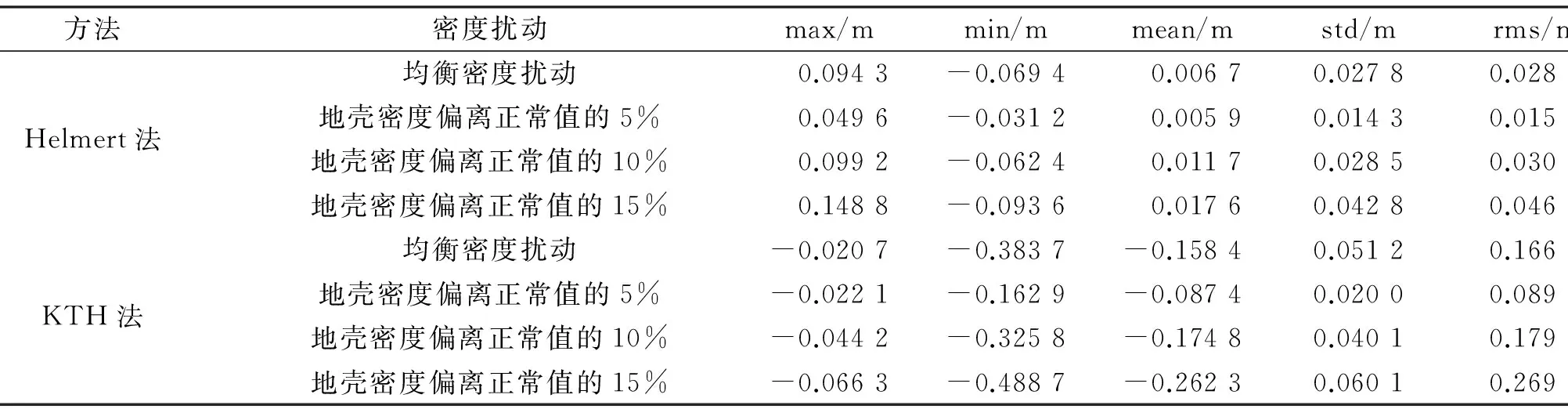
方法密度扰动max/mmin/mmean/mstd/mrms/mHelmert法均衡密度扰动 0.0943-0.0694 0.00670.02780.0286地壳密度偏离正常值的5% 0.0496-0.0312 0.00590.01430.0154地壳密度偏离正常值的10% 0.0992-0.0624 0.01170.02850.0308地壳密度偏离正常值的15% 0.1488-0.0936 0.01760.04280.0462KTH法均衡密度扰动-0.0207-0.3837-0.15840.05120.1665地壳密度偏离正常值的5%-0.0221-0.1629-0.08740.02000.0897地壳密度偏离正常值的10%-0.0442-0.3258-0.17480.04010.1794地壳密度偏离正常值的15%-0.0663-0.4887-0.26230.06010.2691
3 结 语
本文利用Helmert和KTH法模拟试算了不同地形起伏区域横向密度扰动对大地水准面的影响。结果表明,在地形起伏较小、地势较低的平原地区或丘陵地带,横向密度扰动的影响一般不会超过cm级,在精度允许的范围内可以忽略;在地形起伏较大、地势较高的山区,即使横向密度扰动偏离平均地壳密度的5%,对大地水准面的影响也将达到cm级甚至dm级,对于cm级大地水准面的精化而言,需要考虑其影响。此外,Helmert与KTH法解算结果在地形起伏剧烈的山区差异较大,是因为Helmert法计算地形效应时忽略了外区地形质量的影响,其解算结果可能存在偏差,地形起伏越剧烈,可能产生的偏差越大。因此,在地形起伏较大的区域,基于更为严密的KTH法建模的精度更高。由于不同方法对于地形质量的处理方式不同,在地形起伏剧烈的区域建模时可能需要利用多种计算方法基于实测数据分别进行试算,通过计算的变密度大地水准面与实测的GPS水准数据进行比较分析,得到适合该区域的大地水准面建模方法。
[1] 罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报:信息科学版, 2003, 28(3):340-344(Luo Zhicai, Chen Yongqi, Ning Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3):340-344)
[2] Martinec Z, Vaníĉek P, Mainville A,et al. The Effect of Lake Water on Geoidal Height[J].Manuscripta Geodaetica,1995,20:193-203
[3] Huang J, Vaníĉek P, Pagiatakis S,et al. Effect of Topographical Density on Geoid in the Canadian Rocky Mountains[J].Journal of Geodesy,2001,74:805-815
[4] Sjöberg L E. The Effect on the Geoid of Lateral Topographic Density Variations[J]. Journal of Geodesy, 2004, 78:34-39[5] Kiamehr R. The Impact of Lateral Density Variation Model in the Determination of Precise Gravimetric Geoid in Mountainous Area: A Case Study of Iran[J]. Geophysical Journal International,2006,167:521-527
[6] Omang O C, Forsberg R. How to Handle Topography in Practical Geoid Determination: Three Examples[J]. Journal of Geodesy, 2000, 74:458-466
[7] Ramin K. Precise Gravimetric Geoid Model for Iran Based on GRACE and SRTM Data and the Least-Squares Modification of Stokes’ Formula with Some Geodynamic Interpretations[D].Stockholm:Royal Institute of Technology, 2006[8] Sjöberg L E. A Computational Scheme to Model Geoid by the Modified Stokes formual without Gravity Reduction[J].Journal of Geodesy,2003,74:255-268
[9] Sjöberg L E. A General Model of Modifying Stokes’ Formula and Its Least Squares Solution[J].Journal of Geodesy,2003,77:459-464
[10]Sjöberg L E. A Solution to the Downward Continuation Effect on the Geoid Determined by Stokes’ Formula[J].Journal of Geodesy,2001,77:94-100
[11]Sjöberg L E. The Effect of Downward Continuation of Gravity Anomaly to the Sea-Level in Stokes’ Formula[J].Journal of Geodesy,2001,74:796-804
[12]Kuhn M. Geoid Determination with Density Hypotheses from Isostatic Models and Geological Information[J].Journal of Geodesy,2003,77:50-65
The Effect on Geoid Modeling Caused by Lateral Topographical Density Variation
WUYihao1LUOZhicai1,2
1 School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China 2 Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University,129 Luoyu Road, Wuhan 430079, China
Based on the Helmert condensation and the KTH methods, this paper studies the effect on regional geoid modeling caused by the lateral density perturbation. The simulated research shows that the effect on geoid modelling caused by lateral density variation generally does not exceed one centimeter in plains and less undulating areas; these variations can be ignored within the precision limitation. However, for mountainous areas, this effect reaches to the centimeter or even decimeter level, which should be considered carefully in centimeter-accuracy geoid modelling. These effects show significant variation in mountainous areas; the errors are supposed to exist in the results derived from the Helmert condensation method due to neglecting the outer-zone topographical effects. In total, for regional geoid modeling in mountainous areas, various geoids based on variable crust density should be computed by different approaches, and GPS/leveling data can be used to choose the optimal methodology for geoid modeling in these regions.
lateral topographical density variation; geoid; Helmert condensation approach; KTH approach
National Natural Science Foundation of China, No. 41374023.
LUO Zhicai, professor, PhD supervisor, majors in satellite gravity and physical geodesy, E-mail: zhcluo@sgg.whu.edu.cn.
2015-10-14
项目来源:国家自然科学基金(41374023)。
吴怿昊,博士生,主要从事物理大地测量学研究,E-mail: whuwyh@126.com。
罗志才,教授,博士生导师,主要从事卫星重力和物理大地测量学研究,E-mail: zhcluo@sgg.whu.edu.cn。
10.14075/j.jgg.2016.11.013
1671-5942(2016)010-1003-05
P223
A
About the first author:WU Yihao, PhD candidate, majors in physical geodesy, E-mail: whuwyh@126.com.

