MGEX北斗差分码偏差产品质量分析
刘乾坤 隋立芬 肖国锐 陈泉余 王凌轩 曾 添
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
MGEX北斗差分码偏差产品质量分析
刘乾坤1隋立芬1肖国锐1陈泉余1王凌轩1曾 添1
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001

MGEX;差分码偏差;交叠式Allan方差;质量分析;BDS
差分码偏差是影响电离层总电子含量计算以及导航定位的重要误差源[1],未充分校正的差分码偏差会被接收机钟差与模糊度吸收,进而影响精密定位的解算精度与收敛时间[2]。关于BDS DCB的计算模型是当下研究的热点[3-4],但对于其产品却缺乏具体而系统的分析研究。本文提取MGEX北斗系统产品,分析3种DCB产品的精度差异与误差分布规律;针对GEO、IGSO、MEO 3种卫星,对其特异性进行研究,分析周解产品与日解产品的精度差异;最后利用Allan方差初步计算BDS DCB产品的随机误差特性得出,DCB误差特性为白噪声与马尔可夫过程的叠加。
1 DCB计算模型
BDS DCB求解采用与GPS相同的方法,即同时解算电离层总电子含量TEC和DCB。对TEC采用区域多项式模型、区域三角函数模型、全球球谐函数模型以及四维同化模型等方法建模,在一段时间内将DCB作为常数分离出来。
BDS各频点的伪距观测方程可表示为:
(1)

将i、j频点的伪距观测值差分,得到无几何观测值:
(2)

目前北斗卫星端和接收机端参数分离解算的约束条件为所有卫星DCB参数和为0[5]:
(3)

2 MGEX产品质量分析
2.1 DCB产品分析
MGEX发布了3种BDS DCB产品(C2I-C6I, C2I-C7I 和C7I-C6I)。本文选取从2013年年积日1至2015年年积日180(GPS 1 721~1 851周)的BDS DCB产品与GPS 部分DCB产品,其时间序列如图1、图2所示。BDS与GPS产品的误差统计结果如图3、图4所示。结合图1~4可以看出:
1)BDS DCB产品解算误差总体上弱于GPS,但是产品的稳定性优于GPS。GPS卫星由于新老交替,站星分离约束条件发生变化,导致其DCB值跳变,稳定性减弱。
2)DCBB1B2与DCBB2B3从2013年年积日95(1 734周)开始有明显的改变,DCBB1B3从2013年年积日244(1 756周)开始有一个明显的跳变,原因是C30号卫星(2007年发射,现已停用)的值分别在当天被剔除出站星分离约束条件(式(3))。由于未知故障,C13也从2014年年积日294开始停止DCB发布,站星分离的约束条件也随之改变,故在第1 815周所有DCB产品有第二个明显的跳变。

图1 MGEX BDS DCB产品的日解时间序列Fig.1 Time series of MGEX BDS daily DCB

图2 MGEX GPS C1C-C1W 产品的日解时间序列Fig.2 Time series of MGEX GPS daily DCB

图3 BDS 3种DCB产品(DCBB1B2、 DCBB1B3、DCBB2B3)的误差统计结果Fig.3 Statistic errors of the three BDS DCB(DCBB1B2, DCBB1B3 and DCBB2B3)

图4 GPS 3种DCB产品(DCB C1C-C1W、DCB C1C-C2W、DCB C1W-C2W)的误差统计结果Fig.4 Statistic errors of the three GPS DCB(DCB C1C-C1W, DCB C1C-C2W and DCB C1W-C2W)
3)BDS DCB产品整体质量稳定,除个别GEO卫星,其余绝大部分DCB值介于-8~8 ns,误差值都在0.3 ns以内。从选取的连续910 d的数据可以看出,DCB值的曲线非常平滑(除去约束条件变化时的跳变),这也意味着BDS DCB参数可以作一定的预报。
4)DCBB2B3精度最高,误差主要集中在0~0.2 ns,且时间序列曲线更加平滑,锯齿较少。DCBB1B3的误差分布范围明显大于其他两者,在高误差(>0.25 ns)区间内分布较多,且误差绝对值普遍较大。
2.2 DCB闭合差与周解文件分析
表1列出了连续910 d BDS DCB产品值与闭合差(DCBB1B2-DCBB1B3+DCBB2B3)的标准差。表2给出了GPS部分DCB产品值与闭合差(DCBC1C-C1W-DCBC1C-C2W+DCBC1W-C2W)的标准差。对比表1与表2可以看出,BDS DCB产品的标准差大体与GPS相当,闭合差的标准差大于GPS,其稳定性有待提高。从表1可以看出,BDS IGSO卫星DCB标准差最小、精度最高,MEO次之,GEO最差,其中C04号卫星标准差值明显大于其他卫星。DCBB1B2的标准差明显大于其他两者,但其计算误差却较小,这说明其值波动变化较大;DCBB1B3与DCBB2B3的标准差相差较小,其中部分DCBB2B3标准差稍大于DCBB1B3,这主要是因为DCBB2B3有几个较大的误差(可参见图1第1 760 与1 765周的突起)。剔除这两个突起后,两者大体相当。同一卫星不同类型的DCB值中误差差异极大,例如C12号卫星的DCBB1B2中误差达到了0.68,仅次于C04号卫星,但是其DCBB2B3中误差降低到了0.36,小于大部分的卫星。

表1 BDS DCB值以及闭合差的标准差/ns

表2 GPS DCB值以及闭合差的标准差/ns
图5列出了连续910 d BDS与GPS DCB闭合差的时间序列点状图。由于MGEX发布的GPS与BDS 3种DCB都是独立求解,所以并不完全满足闭合差为0的数学关系。表3给出了所有BDS卫星周解结果的DCB值和其闭合差的标准差,从中选取了3颗代表卫星C03(GEO)、C07(IGSO)、C11(MEO),统计其周解误差分布,结果见图6。结合图、表可以看出:
1)图5中1 734~1 760周有一个明显的断层,这段时间C30号卫星没有DCBB1B2、DCBB2B3产品,只发布了DCBB1B3。由于DCBB1B3的计算中引入了不准确的C30号卫星的值,所以其余14颗卫星的闭合差全部减小了0.5 ns,刚好等于C30号卫星的DCBB1B3的值。剔除掉C30后,闭合差立即回归正常。剔除C30卫星后,BDS的DCB产品闭合差精度与GPS大体相当。从第1 816周开始,由于未知原因C13号卫星停止工作,BDS DCB产品的计算同时也剔除了C13号卫星,然而其他卫星并没有如1 734~1 760周产生跳变,闭合差依然稳定。
2)C04号与C05号卫星的闭合差非常不稳定,且变化幅度较大;其余卫星除了在1 762周左右有跳变外,其余时间都较稳定,但是有缓慢发散的变化趋势项。80%左右闭合差位于-0.4~0.4 ns,极少部分(小于1%)大于0.6 ns。不同卫星的闭合差分布范围有较大差异,IGSO卫星的闭合差分布更加集中,质量与稳定性都优于GEO与MEO卫星。
3)对比表1与表2,周解结果的标准差略小于日解结果,但是没有改变不同卫星间的误差大小关系,C04号卫星标准差依然最大,IGSO卫星标准差依然小于GEO、MEO卫星。其中C01号卫星DCBB1B3、DCBB2B3的标准差减小幅度较大,分别从0.51 ns、0.45 ns降低到了0.35 ns、0.36 ns。这也直接导致C01号卫星闭合差的标准差从0.76 ns降低到了0.27 ns。其原因可能是C01小周期误差较多,周解结果平均消解了这些误差,提高了解的精度。

图5 MGEX BDS与GPS DCB产品的日解闭合差时间序列Fig.5 Time series of MGEX BDS and GPS daily closing error DCB

C01C02C03C04C05C06C07C08C09C10C11C12C13C14DCBB1B20.520.430.440.790.610.410.450.490.510.650.450.670.570.64DCBB1B30.350.270.370.580.330.240.230.280.250.360.290.420.310.35DCBB2B30.360.310.590.490.300.270.310.330.280.400.220.360.350.43闭合差0.270.210.170.450.200.180.200.220.170.220.190.280.240.26
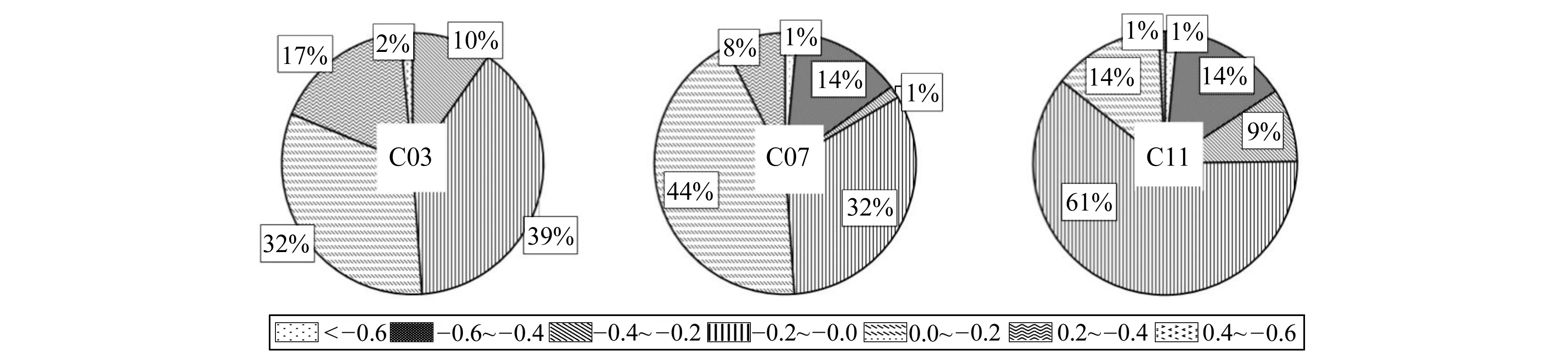
图6 BDS DCB产品的周解闭合差百分比统计结果Fig.6 Statistic misclosure of BDS weekly DCB
3 交叠式Allan方差分析MGEX产品时序

本文提取MGEXBDSDCB值与GPS部分DCB产品构建数据序列,利用交叠式Allan方差计算标准差,选取部分代表卫星的σ(T)-T双对数曲线见图7、图8。根据各自DCB值的Allan方差拟合得到的各种误差成分见表4、表5。由于GPS各卫星噪声参数聚集程度较高、差异较小,故表5只列出了所有卫星的平均值。

图7 部分BDS卫星DCB值的Allan方差Fig.7 Some Allan plot of BDS DCB value

图8 部分GPS卫星DCB值的Allan方差Fig.8 Some Allan plot of GPS DCB value
结合图7、图8和表4、表5可得,除去同频码间偏差DCBC1C-C1W外,GPS与BDS的Allan方差曲线类型基本一致,噪声类型大致为高斯白噪声与一阶马尔可夫过程的叠加,特征点稍有不同;BDS IGSO卫星的WN明显小于GEO/MEO卫星;3种卫星的GM噪声没有明显差异;3种DCB的Allan曲线类型相同,特征点差异明显;同一卫星不同频点白噪声差异可以达到0.09 ns,而相关时间差异可以达到60 d;BDS不同频点信号间微小的差异会非常明显地表现在DCB值上。
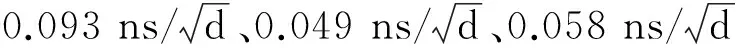
4 结 语
本文通过实验分析MGEX发布的DCB产品的质量,利用Allan方差计算BDS DCB的噪声类型。结果表明:
1)BDS DCB产品质量较好,计算误差一般在0.1~0.2 ns,稍弱于GPS卫星;站星分离的约束条件一直随着在轨卫星的更新而更新;周解文件具有更好的精度与稳定性。

表4 BDS DCB噪声参数

表5 GPS 部分DCB噪声参数
2)BDS IGSO卫星的精度与稳定性最优,其次为MEO卫星,GEO卫星最差。3种DCB产品中DCBB2B3质量与稳定性最优,其次为DCBB1B2,DCBB1B3最差。

致谢:感谢MGEX提供数据支持。
[1] Li Z S, Yuan Y B, Li H, et al. Two-Step Method for the Determination of the Differential Code Biases of COMPASS Satellites [J]. Journal of Geodesy, 2012, 86(11): 1 059-1 076
[2] Guo F, Zhang X H, Wang J L. Timing Group Delay and Differential Code Bias Corrections for Beidou Positioning[J]. Journal of Geodesy, 2015, 89(5):1-19
[3] 樊家琛, 吴晓莉, 李宁翔, 等. 基于三频数据的北斗卫星导航系统DCB参数精度评估方法[J]. 中国空间科学技术, 2013, 33(4):62-70(Fan Jiachen, Wu Xiaoli, Li Ningxiang, et al. COMPASS Satellites DCB Parameter Accuracy Assessment Based on Tri-Frequency Data[J].Chinese Space Science and Technology, 2013, 33(4): 62-70)
[4] Liu Q K, Sui L F, Xiao G R, et al. Refining of BDS Differential Code Bias Model [C].China Satellite Navigation Conference, Xi’an, 2015
[5] 谢益炳, 陈俊平, 伍吉仓, 等. 不同约束条件对电离层电子含量和硬件延迟的影响[J]. 武汉大学学报:信息科学版, 2014, 39(7):799-803(Xie Yibing, Chen Junping, Wu Jicang, et al. Ionospheric Electron Content and Hardware Delay Analysis Based on Different Constraints[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7):799-803)
[6] Allan D W. Statistics of Atomic Frequency Standards [J]. Proceedings of the IEEE, 1996, 54(2):221-230
[7] Riley W J. Handbook of Frequency Stability Analysis[Z]. National Institute of Standards and Technology, 2007
[8] Niu X N, Chen Q J, Zhang Q, et al. Using Allan Variance to Analyze the Error Characteristics of GNSS Positioning[J]. GPS Solutions, 2014, 18(2):231-242
[9] 薛学铭. Allan方差分析测量数据噪声特性的性能研究[J]. 大地测量与地球动力学, 2014,34(6):131-134(Xue Xueming. Study on Properties of Noise Analysis with Allan Variance[J]. Journal of Geodesy and Geodynamics, 2014, 34(6):131-134)
Quality Analysis of MGEX BDS Differential Code Bias
LIUQiankun1SUILifen1XIAOGuorui1CHENQuanyu1WANGLingxuan1ZENGTian1
1 School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China

MGEX; differential code bias; overlapping Allan variance; quality analysis; BDS
National Natural Science Foundation of China,No. 41274016,41174006,40974010;Open Fund of State Key Laboratory of Geographic Information Engineering,No. SKLGIE2013-M-2-1.
SUI Lifen, professor, PhD supervisor, majors in spatial geodetic data processing, E-mail:suilifen@163.com.
2015-09-20
项目来源:国家自然科学基金(41274016,41174006,40974010);地理信息工程国家重点实验室开放基金(SKLGIE2013-M-2-1)。
刘乾坤,硕士生,主要研究方向为GNSS数据处理,E-mail:lqk@whu.edu.cn。
隋立芬,教授,博士生导师,主要研究方向为空间大地测量数据处理,E-mail:suilifen@163.com。
10.14075/j.jgg.2016.11.005
1671-5942(2016)011-0963-05
P228
A
About the first author:LIU Qiankun, postgraduate, majors in GNSS data processing,E-mail: lqk@whu.edu.cn.

