顾及观测值精度的断层变形参数反演研究

张秀霞

1 兰州理工大学土木学院，兰州市兰工坪路287号，730050



顾及观测值精度的断层变形参数反演研究

张秀霞1

1 兰州理工大学土木学院，兰州市兰工坪路287号，730050

从观测值奇异值、观测值分布及反演模型的先验信息3个方面入手，研究观测值对反演结果的影响。以观测点到微分断层的距离倒数为权，构建顾及观测值权值影响的反演模型。以位错理论为基础，结合遗传算法，对龙门山断裂带进行三维滑动速率反演研究。结果表明，经过奇异值剔除的数据应用于顾及观测值权值的反演模型，给定合理的“先验信息”，其结果比已知观测值直接参与反演模型更稳定、可靠。

反演；位错模型；奇异值；断层；遗传算法

位错理论模型模拟断层三维滑动速率的研究多集中在智能算法的改进[1]、单一数据反演[2-3]或多种大地测量数据联合反演[4-5]等以寻求最佳模拟效果。好的反演结果依赖于高质量的数据、可靠的模型、合理的先验信息、稳定的算法。而反演的困难之一就是观测资料不完备，所获得的数据总是局部的、变形体表面的，不能很好地体现变形体的变形特征；困难之二是任何观测都存在干扰，而微小的干扰即可使反演结果产生大的波动[6]。本文拟从观测值奇异值、GPS观测值距断层距离远近及反演模型的初值信息等方面对比分析，结合位错理论，应用全局最优遗传算法，以龙门山断裂带为对象进行研究分析。

1 方法与模型

1.1 观测数据奇异值的检验

在变形监测中，观测数据避免不了有奇异值的存在，在数据分析及应用之前有必要将其剔除。本文采用“3σ准则”剔除奇异值，具体推导及计算见文献[7]。

1.2 遗传算法

遗传算法[8]是模拟自然遗传机制的人工智能搜索算法，其主要特点是全局搜索及局部个体的信息交换。如果把现实问题的解作为个体，根据一定的约束条件选择子个体，子个体继承父个体的优良基因，不断改进，以寻求全局最优解。遗传算法应用中主要考虑的参数有种群大小M、交叉概率Pc以及变异概率Pm等。在本文的程序中，顾及算法时间效率及解的质量等问题，在反演计算时分别取M=500，Pc=0.75，Pm=0.05。

1.3 弹性位错模型及其改进

位错理论模型可以模拟断层三维滑动速率与GPS观测位移场之间的关系。图1中，为更好地模拟断层的滑动特性，将断层分段，fi为断层的微分断层，则每个微分断层面上任意点与地面点的位移关系可以通过断层面上的滑动位移表示：

ui=

(1)

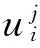
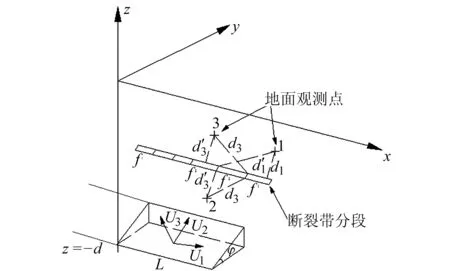
x轴与断层走向平行，y轴垂直于断层走向，z轴垂直地平面向上。Ui(i=1,2,3)表示断层走向、倾向和法线方向的滑动量。f1,f2,f3,…,fi表示断裂带分段，+表示部分地面观测数据，di和表示各观测点到两个微分断层的最短距离图1 矩形位错分段模型Fig.1 Subsections model of rectangle dislocation rectangle dislocation model

在断层反演中，用有限的N个数据求解连续的模型是欠定性问题，难以求解。如果观测值数量越多，效果越佳，但是在实际工作中会使工作量增加，成本提高，故在实际应用中应该将“模型”和数据取折衷[9]。又因为观测数据分布不均，部分点离某些断层较近，能较好地反映其滑动特征，而另外一部分观测数据虽能体现断层滑动特征，但其作用甚微。为此，本文在断层几何模型参数给定的情况下，结合断层分段思想，以观测点到微分断层的距离(即点到线段的最短距离)倒数为权，构造优化模型，构建顾及观测值权值影响的目标函数：

(2)

式(2)表示通过位错理论计算的微分断层的地面位移场与实际观测值残差的加权平方和最小。式中，Pi为各观测点距离微分断层的最短距离的倒数；ui(m)为第i个观测点由微分断层几何模型参数m计算的位移；ui(o)为GPS观测位移量。本文采用倒数变化建立基于遗传算法的适应度函数：

Fix(x)=1/E

(3)

2 算例及结果分析

2.1 正演结果模拟计算

为检验本文数据处理方法及模型的有效性和正确性，采用文献[10]断层几何模型参数{F=f(D)=(E=92.889，N=35.897，L=70.188，W=16，d=14，φ=-7，δ=88)}及正演模拟结果的GPS数据作为已知数据，将数据人为加入5%的噪声和10%的噪声作为观测数据直接进行反演计算，利用C语言结合位错理论编写基于遗传算法的反演程序，计算过程为读取断层数据、GPS数据，直接进行反演计算得出断层三维滑动速率，结果见图2(a)。在此基础上对程序进行改进，在读入GPS观测数据后先进行奇异值剔除，并计算各观测点到每个微分断层的最短距离，再将加入噪声的观测值读入顾及观测值权值影响的反演模型计算断层三维滑动速率，结果见图2(b)。

从图2看出，加入5%和10%的噪声的观测数据直接进行反演计算结果波动较大，用时1～2 s(图2(a))；经过噪声剔除的数据应用于顾及观测值权值的反演结果更接近真值，结果较为稳定，并且收敛速度明显提高，用时<1 s(图2(b))。断层走滑反演结果较好，而倾滑分量和张开分量结果不甚理想，故在反演时可联合水准、重力等资料进行反演。从理论值角度出发，不论是加入5%还是10%的噪声数据,经过奇异值剔除，应用于反演模型，结果应该是相同的，但本文出现不一致的情况，可能是因为本文使用的奇异值剔除方法没有考虑两端的数据噪声，导致数据的微小变化，引起了反演参数的不一致。

图2 模拟反演结果对比Fig.2 Comparison of simulation inversion

2.2 龙门山断裂带三维滑动速率反演模拟

龙门山断裂带也称龙门山断层，是中国西北典型的逆冲断层，由龙门山后山断裂、龙门山主中央断裂、龙门山主边界断裂组成，长约500 km，宽约70 km。为更好地体现断层的真实模型效果，本文利用断裂的分布排列等几何学特征进行断裂形态的几何分段。利用断层微分思想，将龙门山3条主要断裂细分为20个子断层，详见参考文献[10]，主干断裂与微分断层分布见图3，各微分断层分别用不同的线型表示。

文中使用南北地震带2004～2007年GPS观测数据，如图3所示，箭头长短表示位移量大小，箭头方向表示位移方向。图3中，数据点分布较为分散，离龙门山较近的点位移量较小，更能体现断层地面位移大小，故在反演断层三维滑动速率时，这部分点应该赋以较大权重；而离龙门山断层较远的点位移量虽然较大，但在反演计算时应赋以相对较小权重。将已知数据代入本文建立的反演模型，对反演模型补充一定的“先验信息”，即为将要反演的每个子断层单元3个位错量(U1,U2,U3)初始值分别取值在[-5，5]、[-5，5]、[-5，5](单位为mm/a)，反演结果见表1。

表1中，U1、U2、U3分别表示断层的走滑、倾滑、张开运动分量，U1分量负号表示右旋，U2分量负号表示逆冲，U3分量负号表示挤压。反演结果中各微分断层三维滑动值不尽相同,反映了断层运动空间分布的异质性。整体走滑值体现出右旋走滑特征，且由北向南有增强趋势，个别子断层(经纬度分别为104.945 33°/32.067 09°和104.562 62°/32.113 64°两个子断层，编号为16和17)走滑特征反映为微弱的左倾，结合图3可知，其与该微分断层处GPS观测值走向为NW向有关。走滑总体值小于2 mm/a；倾滑分量数值整体较小，小于1.6 mm/a，整体表现为逆倾；张开分量数值小于1.3 mm/a，整体表现为挤压，与地质、地貌结果一致[11-13]。

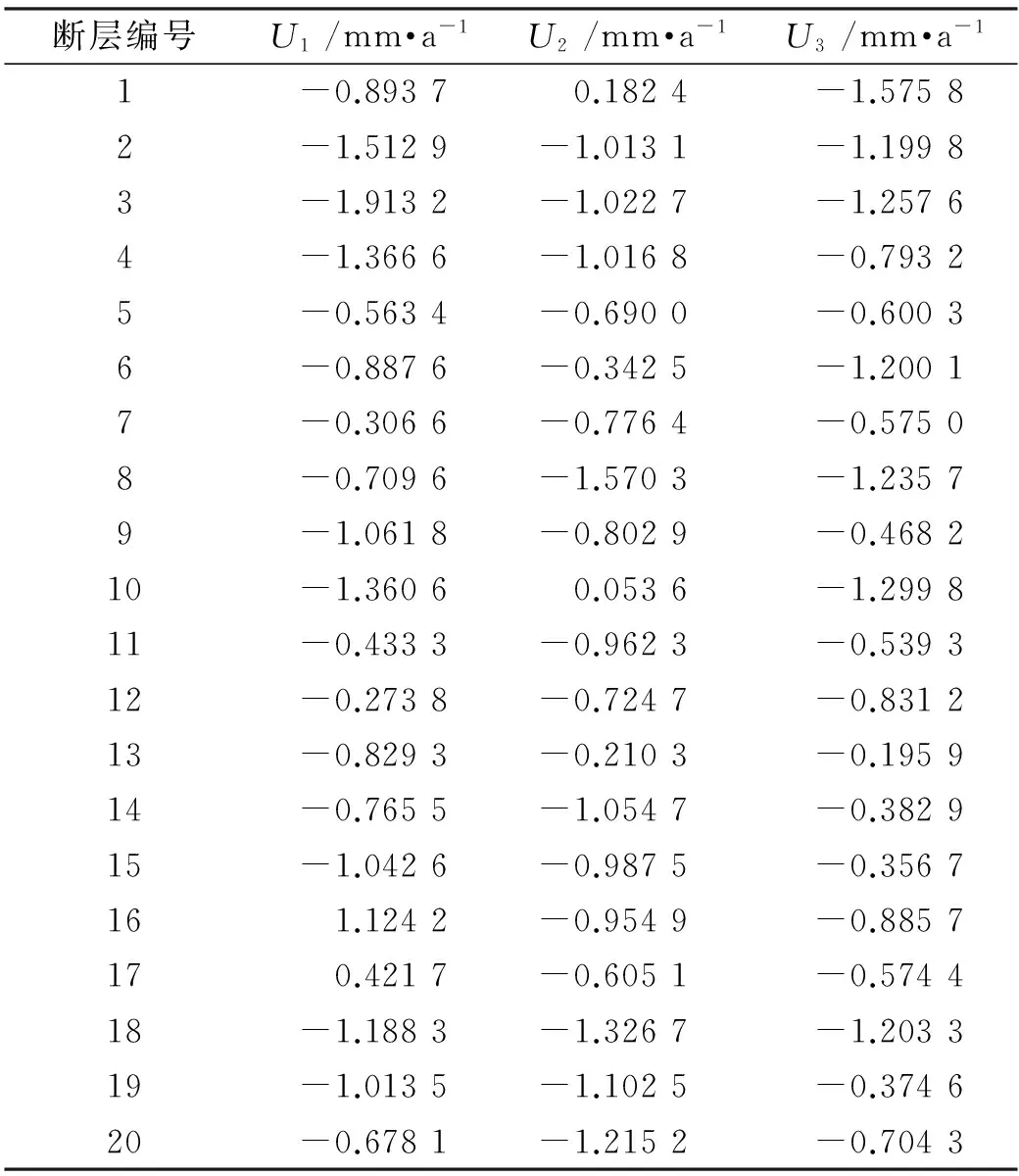
表1 反演结果

在断层其他参数不变的情况下，调整反演模型补充的“先验信息”，将每个子断层单元3个位错量(U1,U2,U3)初始值分别取值在[-10，10]、[-10，10]、[-10，10](单位mm/a)。反演结果显示，龙门山南段部分子断层(经纬度分别为103.264 13°/30.704 66°和103.136 31°/30.814 07°子断层，编号为6和7)走滑分量有变大趋势，数值为5.101 1 mm/a、4.283 6 mm/a。出现此问题的原因可能与给定初值的范围有关，该结果与李志才等研究结果相符[14]。其他分量无明显变化，表明反演结果有很好的稳定性。

3 结 语

对GPS观测值进行奇异值检测预处理，并将预处理结果与原始观测值进行反演计算分析，结果表明：1)“3σ准则”可有效剔除GPS奇异值，剔除奇异值后的观测数据对算法的干扰性减小，反演结果更为稳定；2)顾及观测值精度影响的反演模型能更好地模拟断层的相关性质，并且算法收敛速度更快；3)真实变形特征。

由于条件所限，文中对GPS观测数据仅考虑了奇异值、点的分布等信息，没有顾及观测值系列长短对反演结果的影响。此外，为更加准确地凸显观测值精度对反演结果的影响，本文中对所有的子断层几何模型参数赋以定值，没有考虑断层模型参数的变化。

[1] 刘宁,张永志.位错模式的蚁群算法反演断层参数[J].大地测量与地球动力学.2009，29(1):31-35(Liu Ning, Zhang Yongzhi.Fault Parameter Inversion with Ant Colony Algorithm by Dislocation Model[J].Journal of Geodesy and Geodynamics.2009, 29(1):31-35)

[2] 张永志,王卫东,魏玉明,等.用GPS资料反演祁连山断层的三维滑动速率[J].大地测量与地球动力学, 2006,26(1):31-35(Zhang Yongzhi,Wang Weidong,Wei Yuming,et al. Inversion of 3-D Slip Velocity of Qilianshan Fault with GPS Data[J]. Journal of Geodesy and Geodynamics,2006,26(1):31-35)

[3] 谈洪波,玄松柏,杨光亮,等.滇西断裂运动的重力反演[J].大地测量与地球动力学,2013,33(6):10-15(Tan Hongbo, Xuan Songbai, Yang Guangliang,et al. Gravity Inversion of Faults Movement in Western Yunnan[J]. Journal of Geodesy and Geodynamics,2013,33(6):10-15)

[4] 富宇宁,许才军.水准和重力数据联合反演中权问题的研究[J].大地测量与地球动力学,2007,27(2):68-74(Fu Yuning, Xu Caijun. On Relative Weight Problem in Joint Inversion Using Levelling and Gravity Data[J]. Journal of Geodesy and Geodynamics,2007,27(2):68-74)

[5] 张希,江在森,王双绪,等.青藏块体东北缘GPS与水准资料的三维负位错联合反演[J].国际地震动态,2007(7):61-66(Zhang Xi, Jiang Zaisen,Wang Shuangxu,et al. United Inversion of Three-Dimensional Negative Dislocation for GPS and Leveling Observation in Northeastern Margins of Qinghai-Tibet Block[J]. Recent Developments in World Seismology,2007(7):61-66)

[6] 赵少勇,陶本藻,于正林.论变形测量数据的反演[J].测绘学报,1992,21(3):21(3)161-171(Zhao Shaoyong, Tao Benzao,Yu Zhenglin. On Inversion of Deformation Survey Data[J].Acta Geodaetica et Cartographica Sinica,1992,21(3):21(3)161-171)

[7] 黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010(Huang Shengxiang,Yin Hui,Jiang Zheng. Data Processing of Deformation Monitoring[M].Wuhan:Wuhan University Press, 2010)

[8] 陈国良,王煦法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,1996(Chen Guoliang,Wang Xifa,Zhuang Zhenquan,et al. Genetic Algorithms Theory and Applications[M].Beijing:Post &Telecom Press,1996)

[9] 王家映.地球物理反演理论[M].北京:高等教育出版社,2012(Wang Jiaying. Inversity Theory in Geophysics[M]. Beijing:Higher Education Press,2012)

[10]张秀霞.顾及误差的遗传算法反演研究[D].西安:长安大学,2010(Zhang Xiuxia. Inversion Study of Genetic Algorithm Based on Errors[D]. Xi’an:Chang’an University,2010)

[11]杨晓平,蒋溥,宋方敏，等.龙门山断裂带南段错断晚更新世以来地层的证据[J].地震地质,1994,21(4):534-631(Yang Xiaoping,Jiang Pu,Song Fangmin, et al. The Evidence of the South Longmenshan Fault Zones Cutting Late Quaternary Stratum[J].Seismology and Geology,1994,21(4):534-631)

[12]王二七,孟庆任,陈智梁,等.龙门山断裂带印支期左旋走滑运动及其大地构造成因[J].地学前缘,2001,8(2):375-384(Wang Erqi,Meng Qingren,Chen Zhiliang,et al. Early Mesozoic Left Lateral Movement along the Longmenshan Fault Belt and Its Tectonic Implications[J]. Earth Science Fromntiers,2001,8(2):375-384)

[13]李勇,周荣军,Densmore A L ,等.青藏高原东缘龙门山晚新生代走滑-逆冲作用的地貌标志[J].第四纪研究,2006,26(1):40-51(Li Yong,Zhou Rongjun,Densmore A L ,et al. Geomorphic Evdence for the Late Cenozoic Strike-slipping and Thrusting in Longmen Mountains at the Eastem Margin of the Tibetan Platean[J].Quatemary Science, 2006,26(1):40-51)

[14]唐文清,刘宇平,陈智梁,等.基于GPS技术的活动断裂监测——以鲜水河、龙门山断裂为例[J].山地学报,2007,25(1):103-107(Tang Wenqing,Liu Yuping,Chen Zhiliang,et al. Monitoring of Faults Activity Based on GPS[J].Journal of Mountain Science,2007,25(1):103-107)

About the author:ZHANG Xiuxia,lecturer,majors in application of 3S technology, E-mail: lutzxx@163.com.

Inversion of Fault Deformation Parameters Considering Observation Precision

ZHANGXiuxia1

1 School of Civil Engineering, Lanzhou University of Technology,287 Langongping Road, Lanzhou 730050, China

The influence of observation precision to inversion results is studied from singular value, the distribution of data and a priori information of the inversion model. To take the reciprocal of the shortest distance between observation and the subdivision fault for weight, the model considering observation precision is established. On the basis of the dilocation model, the velocity of Longmenshan fault is calculated by GA. The results show that the data out of singular values, with the model considering observation precision, on the premise of reasonable a priori information, are stable and reliable.

inversion；dilocation model； singular value；fault；genetic algorithm

National Natural Science Foundation of China, No.51578274; Alumni Foundation of Civil Engineering 77, Lanzhou University of Technology, No.TM-TJ-1402.

2015-11-16

项目来源：国家自然科学基金(51578274)；兰州理工大学建工七七基金(TM-TJ-1402)。

张秀霞，讲师，主要从事3S技术应用研究，E-mail：lutzxx@163.com。

10.14075/j.jgg.2016.11.008

1671-5942(2016)011-0977-04

P315

A