改进的最优非负变权组合模型及其应用

吴少华 程朋根，2 付 博

1 东华理工大学测绘工程学院，南昌市广兰大道418号，330013 2 流域生态与地理环境监测国家测绘地理信息局重点实验室，南昌市广兰大道418号,330013



改进的最优非负变权组合模型及其应用

吴少华1程朋根1，2付 博1

1 东华理工大学测绘工程学院，南昌市广兰大道418号，330013 2 流域生态与地理环境监测国家测绘地理信息局重点实验室，南昌市广兰大道418号,330013

根据GM(1，1) 、BP神经网络、卡尔曼滤波的特点，建立以灰色关联度最大为准则的最优非负变权组合预测模型，在一定程度上抑制了误差“放大”的效应。与以误差平方和最小为准则的变权组合模型、各最优加权组合模型、各单一模型进行对比分析，结果表明，本文模型预测精度最高。

大坝变形；最优组合；灰色关联度；非负变权

大坝变形数据处理方法有灰色模型、BP神经网络、卡尔曼滤波，回归分析等，但单一的预测模型有时不能很好地反映真实的变形趋势，有一定的局限性[1-2]。灰色模型[3]因建模简单而被广泛运用于各行各业，然而其仅适用于短期预测，对于非线性形态不具有很好的预测效果；BP神经网络[4]虽然具有较强的非线性处理能力，但受网络的权值与阈值的影响较大，容易陷入局部最小值；卡尔曼滤波[5]受观测条件的限制比较大。不同的预测方法会提供不同的有用信息，如果将某些预测精度较低的预测方法摒弃掉，就会导致某些有用信息的缺失[6]。

自1969年Bates和Granger[7]首次提出了组合预测模型以来，越来越多的学者研究组合预测模型并取得辉煌的成果。与此同时，广大的测绘学者也将组合预测运用于变形分析与预报中。潘国荣等[8]建立了最优加权组合预测模型，取得了较好的预测精度，但是这并不合理，因为在实际变形监测数据预测中，不同模型在同一时间段内的预测精度有时不同，如果赋等同的权值，那么难免会丢失一些有效信息。为此，吴清海等[9]将变权组合应用于建筑物的水平位移预测，预测精度有了进一步提高。任超等[10]将变权组合预测模型运用于大坝变形分析，并与最优加权组合结果对比，提高了模型精度。然而，以上变权组合模型是建立在误差平方和最小的前提下，这存在一定的缺陷。因为模型受异常数据的影响较大时，容易产生误差“放大”的现象，不具备良好的稳健性。

针对大坝变形小样本数据同时具有趋势性和随机波动的特点，本文引进更具稳健性的灰色关联度[11]，建立以灰色关联度最大为准则的变权组合预测模型，并运用于大坝变形分析中。然后与以误差平方和最小为准则的变权组合模型、各最优加权组合模型、各单一模型进行对比分析。实验结果表明，本文方法的预测精度最高，预测效果最佳。

1 组合模型定权准则

1)灰色关联度准则

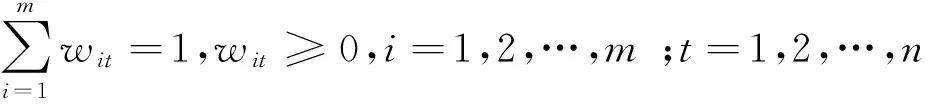
(1)

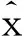
(2)

设γ为组合预测模型的灰色关联度，根据式(1)与(2)得：

(3)

式中，γ为权系数向量W=(w1t,w2t,…,wmt)的函数，一般来说，组合预测方法的灰色关联度γ越大，模型越有效。因此，以灰色关联度为准则的最优模型为：

maxγ(W)=

(4)

2)误差平方和准则

如前面定义，令组合模型的误差平方和为F，则以误差平方和最小为准则求解权系数的问题可以归结为以下最优模型：

(5)

本文分别以灰色关联度最大、误差平方和最小为目标函数，通过规划方法求解最优变权系数。

2 模型精度评价

为了综合评估模型的效果，采用平方和误差、均方根误差、平均绝对值误差、平均绝对百分比误差和平均绝对百分比误差精度指标评价模型[6]：

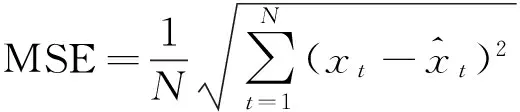
平均绝对百分比误差

平均绝对百分比误差

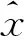
3 实例分析

本文以文献[10]某混凝土坝水平位移监测数据为例。该大坝在重要结构体上布设了7个水平位移监测点，选其D4号点水平位移数据建立组合预测模型。从大坝水平位移曲线可以发现，在1～5、8～14期数据变化平稳，而其他几期上下浮动较大，说明变形不稳定，具有较强的随机性，呈非线性变化趋势。选取变形分析数据处理常用的方法(灰色GM(1，1)模型、BP神经网络、卡尔曼滤波)作为组合预测模型的参考方案，前11期作为拟合区，后10期作为预测区。表1为各模型的预测值。

由表1可以看出，12～14期变化平稳，3种模型的预测值都与实际值接近。但是在变形急剧变化的第15～21期，各模型的预测值都偏离实际值较大，其中灰色GM(1，1)最大残差达到-2.11mm，BP神经网络最大残差达到1.76mm，即便是卡尔曼滤波的残差最大值也达到-1.91mm，这说明在非平稳阶段3种模型的预测值未能满足监测的要求。显然，如果用单一模型预测，很难得到较优的全局预测值。

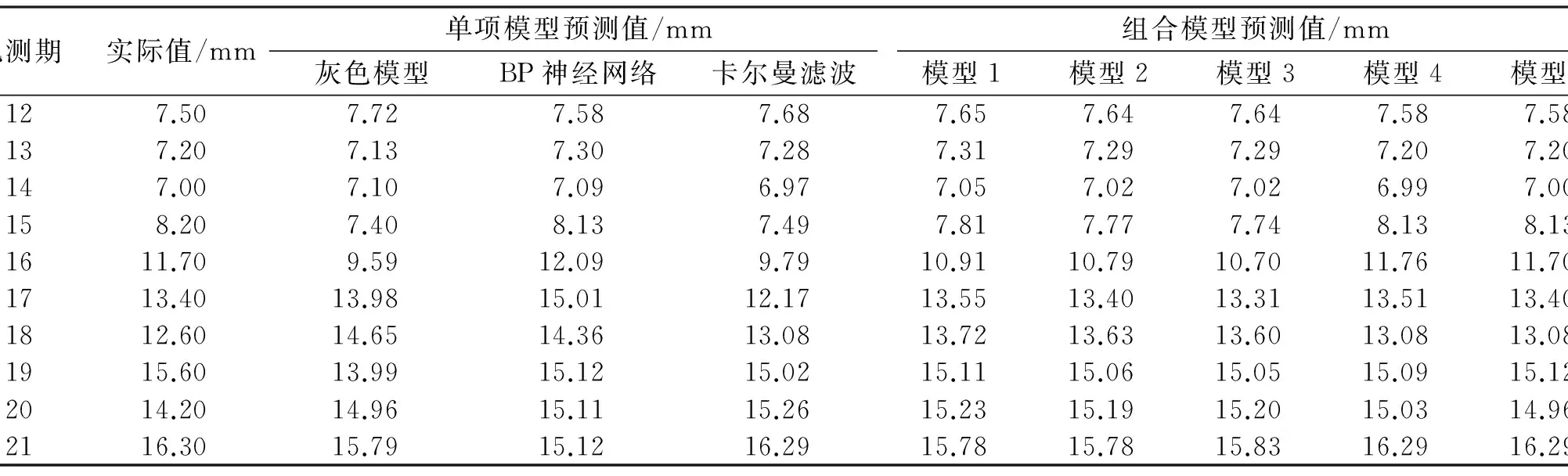
表1 各模型的预测值比较

因此，本文通过构建5种组合预测模型对大坝水平位移数据进行分析。模型1：以误差平方和最小为准则的最优加权组合模型；模型2：以误差绝对值和最小为准则的最优加权组合模型；模型3：以最大绝对值误差最小为准则的最优加权组合模型；模型4：以误差平方和最小为准则的最优变权组合模型；模型5：以灰色关联度最大为准则的最优变权组合模型。从表1可以看出，3种单项预测模型的预测精度有高有低，经过计算得出不同加权组合模型的权值，然后根据式(1)～(5)计算不同准则下的变权系数，具体结果如下：

式中，W1为模型1的加权系数向量，W2为模型2的加权系数向量， W3为模型3的加权系数向量，W4为模型4的变权系数向量，W5为模型5的变权系数向量。最后将各组合预测模型的最优非负权系数向量代入各变权组合模型中，得到各组合模型的预测值(表1)。从表1中不难发现，最优加权组合模型的预测效果都比各单预测模型效果好，其中最优加权组合模型的最大残差为-1.123 6 mm，最小残差为-0.087 7 mm，预测精度明显提高。而最优非负变权组合不管是预测值与残差都优于最优加权组合预测值，其中基于误差平方和最小的变权组合最大残差值为0.83 mm，最小残差为0；本文方法求出的预测值与原始水平位移值之间的最大残差为0.76 mm<0.83 mm，最小残差为0。这说明本文的方法预测精度比前者高。

由图1可知，12～15期各模型的预测值都比较符合实际水平位移值。然而在15～21期，3种单项预测模型偏离原始水平位移值较大，但是经过最优组合之后，各组合模型的预测值比较接近实际值，而且残差也小于各单项预测模型。而最优非负变权组合模型根据单一模型对各期预测精度的高低赋予不同权值，在一定程度上克服了最优加权组合模型的局限性，预测结果明显优于最优加权模型，但在15～21期模型4的预测值仍大于原始水平位移值。通过本文方法求得的预测值比模型4更接近实际值，这是因为本文方法有效抑制了误差的“放大”效应，进而说明本文方法有很好的稳健性。

图1 各模型预测值对比Fig.1 Comparison the values of the models

为了直观反映各模型的预测精度，按照上文评价方法分别计算各模型的精度指标(表2)。

表2 各模型精度比较

由表2可以发现，组合模型的精度都高于单一预测模型，其中最优非负变权组合预测模型的预测精度优于最优加权组合预测模型，可见最优非负变权组合模型在一定程度上保证了较好的全局预测精度，具有一定的优越性。本文方法比文献[10]的预测精度又有所提高。

4 结 语

本文将基于最大灰色关联度的最优非负变权组合模型引入大坝变形监测中，在一定程度上抑制了以误差平方和最小为准则的最优变权组合模型产生的误差“放大”问题，进而提高了模型的稳健性。然后通过灰色关联度的改变来改进组合模型的权重，结果发现本文方法的综合精度优于文献[10]和其他最优加权组合模型以及各单一模型，说明本文方法能有效提高大坝变形预测的精度，对变形预测有一定的研究价值。

[1] 覃劭峰. 基于GM(1，1)-ARIMA最优组合的大坝预测模型[J]. 测绘通报，2014(S2)：66-69(Qin Shaofeng. The Optimal Combination of Dam Deformation Based on GM(1，1)-ARIMA Models[J]. Bulletin of Surveying and Mapping，2014(S2)：66-69)

[2] 王新洲, 范千, 许承权,等. 基于小波变换和支持向量机的大坝变形预测[J]. 武汉大学学报：信息科学版, 2008, 33(5):469-471(Wang Xinzhou，Fan Qian, Xu Chengquan,et al. Dam Deformation Predictions Based on Wavelet Transforms and Support Vector Machine(SVM)[J]. Geomatics and Information Science of Wuhan University， 2008，33(5):469-471)

[3] 何君，杨国东. 灰色预测理论在建筑物沉降中的应用研究[J]. 测绘通报，2012(3)：63-64(He Jun, Yang Guodong. On the Application of Grey Theory to Building Settlement[J]. Bulletin of Surveying and Mapping，2012(3)：63-64)

[4] 秦真珍，杨帆，黄胜林，等. 基于GA-BP算法的大坝边坡变形预测模型[J]. 测绘工程，2010，19(1)：13-16(Qin Zhenzhen，Yang Fan，Huang Shenglin，et al. Dam Side Slope Deformation Forecast Model Research Based on GA-BP Algorithm[J]. Engineering of Surveying and Mapping，2010，19(1)：13-16)

[5] 文鸿雁，周吕，韩亚坤，等. 基于卡尔曼滤波的GM(1，1)模型在高铁隧道变形分析中的应用[J]. 大地测量与地球动力学，2014，34(1)：88-91(Wen Hongyan，Zhou Lü，Han Yakun，et al. Application of GM(1，1) Model Based on Kalman Filter to the Subsiding Analysis of High-Speed Railway Tunnel[J]. Journal of Geodesy and Geodynamics，2014，34(1)：88-91)

[6] 陈华友. 组合预测方法有效性理论及其应用[M]. 北京：科学出版社，2008(Chen Huayou. Combination Forecast Method and Its Application[M]. Beijing:Science Press，2008)

[7] Bates J M, Granger C W J. The Combination of Forecasts[J]. Journal of the Operational Research Society, 1969, 20(4): 451-468

[8] 潘国荣，谷川. 形变监测数据组合预测[J]. 大地测量与地球动力学，2006，26(4)：27-29(Pan Guorong， Gu Chuan. The Combination Forecast of Deformation Monitoring Data[J]. Journal of Geodesy and Geodynamics，2006，26(4)：27-29)[9] 吴清海，李惠芳. 变权组合模型在沉降预测中的应用 [J]. 测绘科学技术学报，2009，26(2)：118-120(Wu Qinghai，Li Huifang. The Application of Variable Weight Combination Model in Subsidence Prediction[J]. Journal of Geomatics Science and Technology，2009，26(2)：118-120)

[10] 任超，梁月吉，庞光锋，等.最优非负变权组合模型在大坝变形中的应用[J]. 大地测量与地球动力学，2014，34(6)：162-166(Ren Chao，Liang Yueji，Pang Guangfeng，et al. Application of the Optimal Non-Negative Variable Weight Combination Model for Monitoring Dam Deformation[J]. Journal of Geodesy and Geodynamics，2014，34(6)：162-166)

[11] 陈亮，黄腾. 基于灰色关联分析的卡尔曼滤波在桥梁变形监测中的应用[J]. 测绘工程，2010，19(4)：47-49 (Chen Liang， Huang Teng. The Application of Kalman Filtering Based on Grey Correlation Analysis in the Deformation Monitoring of Bridge[J]. Engineering of Surveying and Mapping，2010，19(4)：47-49)

Application of the Improved Optimal Non-Negative Variable Weight Combination Model

WUShaohua1CHENGPenggen1,2FUBo1

1 Faculty of Geomatics, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China2 Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG,418 Guanglan Road, Nanchang 330013, China

According to the characteristics of GM (1,1), BP neural network and Kalman filter, we propose an optimal non-negative variable weight combination forecasting model based on grey correlation. This new model can control the effects of the errors. The calculation results are compared with the variable weight combination model based on the error square of minimum and the optimal weighted combination model or the three single method. The results show that the new model has the highest accuracy.

dam deformation；optimal combination；grey correlation；non-negative variable weight

National Natural Science Foundation of China，No.41161069；Scientific Research Fund of Jiangxi Provinces，No. GJJ12384；Graduate Education Fund of Mapping Geographic of Jiangxi Provinces.

CHENG Penggen，professor, PhD supervisor, majors in GIS theory and its engineering application, remote sensing mapping in geoscince, data processing in surveying and mapping, E-mail: 407308636@qq.com.

2015-12-13

项目来源：国家自然科学基金(41161069)；江西省教育厅科技项目(GJJ12384)；测绘地理信息江西省研究生教育创新基地项目。

吴少华，硕士生，主要研究方向为变形监测技术与数据处理，E-mail：wshecit@163.com。

程朋根，教授，博士生导师，主要研究方向为地理信息系统理论与工程应用、遥感地学制图、测绘数据处理， E-mail: 407308636@qq.com。

10.14075/j.jgg.2016.11.006

1671-5942(2016)011-0968-04

P258

A

About the first author:WU Shaohua，postgraduate，majors in data processing and deformation, E-mail:wshecit@163.com.