纤维土在普通地基条件下的力学性能数值模拟研究

宫 剑 （淮南市城建档案馆，安徽 淮南 232001）

纤维土在普通地基条件下的力学性能数值模拟研究

宫 剑 （淮南市城建档案馆，安徽 淮南 232001）

作为一种新的路用材料，纤维土具有一般加筋土所没有的近似各向同性的力学性能[5,6]。借助ABAQUS软件对道路路床和底基层在添加纤维后所表现出来的力学性能进行数值模拟分析，得出结论：在底基层掺加纤维时，对道路表面最大压应力和最大位移的影响很小；随底基层纤维含量的增加，底基层底部的最大水平拉应力逐渐减小；在路床掺加纤维时，随路床纤维含量的增加，道路表面的最大水平压应力逐渐减小，底基层底部的最大水平拉应力也逐渐减小；但随路基高度的增加，纤维含量的变化对水平应力的影响逐渐减小。最后给出不同路基高度条件下的纤维土加固对象和最佳配合比。

纤维土；力学性能；数值模拟；最佳配合比

目前，路基常用材料为石灰土、二灰土和水泥土等，但它们都有着共同的缺点，收缩系数较大，抗弯拉强度较低，容易产生裂缝。

利用在土中掺加连续不断的纤维材料而对土体进行加固——“纤维土法”，是一种目前应用还不普遍的方法，该方法的加固机理可概括为“弯曲机理”和“交织机理”。弯曲机理是指纤维在土中的分布形态是由无数个弯曲转折组成的，当土体承受外力从而使纤维受拉时，在纤维弯曲的凹侧就会产生纤维对土颗粒的压力和摩擦力，从而起到加固土体的作用；交织机理是指由于土中无序分布的纤维存在着无数的交织点，如果在纤维的交叉处受到力的作用，从而有位移的趋势，就会遇到其它纤维阻止这种位移，即任何一段纤维的受力变形都会牵动与之交织的各个方向的纤维，从而形成空间的三维受力区[1-4]。

基于以上两种机理，在土体中掺加纤维对路基进行加固，可提高路基的整体性、抗拉能力和承载力。本文借助ABAQUS软件建立道路结构层的三维立体模型，分析在底基层、路床掺加纤维时对结构层水平应力和位移的影响情况，得出不同路基高度下的纤维土的加固对象和最佳配合比。

数值模型为三维立体模型如图1。包括路面、路基、土基和加载块，其中路面包括面层（厚度0.15m）、基层（厚度0.25m）、底基层（厚度0.25m）、路肩和中央分割带，路基包括路床（厚度0.8m）和路堤（厚度为1.2m和4.2m），地基土体厚度为10m，加载块模拟车辆轮胎加载，布置图见图2。路面宽度为28m，放坡坡度为1：1.5，地基土体宽度为60m。取道路走向20m宽度进行研究。各层之间均采用TIE进行联结。

图1 计算模型

图2 车辆轮胎加载示意图

模型中的各结构层在道路走向两侧约束道路走向方向的位移，地基在垂直道路走向两侧也约束道路走向方向的位移，在地基的底面约束全部位移。

为了更好地模拟填筑与施加车辆荷载的过程，计算中先进行地应力平衡，然后分级施加路堤、路床、路面结构和车辆荷载，采用ABAQUS中的时间步(Time Step)命令来控制路堤和路面分级加载情况，将道路结构分为3层进行增量分析，每层填筑时间和施工间歇期均为为30d。道路填筑完后施加车辆荷载。

本模型中共引进5种材料，其中面层和基层用线弹性模型模拟，参数见表1；基层和路床采用Mohr-Coulomb模型模拟，材料参数：φ=35°，c=40.0kPa，E=7.0MPa。

线弹性材料参数 表1

本计算中主要考虑路基高度、路床和路面底基层掺加不同配比纤维三个因素，具体见表2。模拟2m和5m两种路基高度下纤维土对路床或底基层的任一层进行改善，试验方案见表3。

主要因素与水平 表2

试验方案 表3

在普通土基条件下，路基高度分别为2m和5m时，道路各结构层应力和位移示意云图如图3～6。

图3 路基高度为2m道路应力示意图

图4 路基高度为2m道路竖向位移示意图

图5 路基高度为5m道路应力示意图

图6 路基高度为5m道路竖向位移示意图

路面按两个方向对称布载，加载后，道路表面和底基层底部的最终竖向位移沿x方向变化曲线如图7和图8。

图7 面层表面竖向位移沿x方向分布

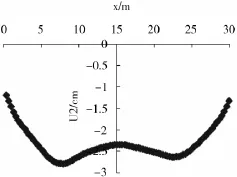
图8 路面底基层底部竖向位移沿x方向分布

从图7、8得知，道路表面和底基层底部的最大竖向位移均发生在车辆后轮的作用点处；随深度的增加，车辆作用点处产生较大位移的优势逐渐减小，W型逐渐向U型发展。

在不同路床、底基层材料和不同路基高度下，进行计算得到道路表面和底基层底部的最大位移见表4。

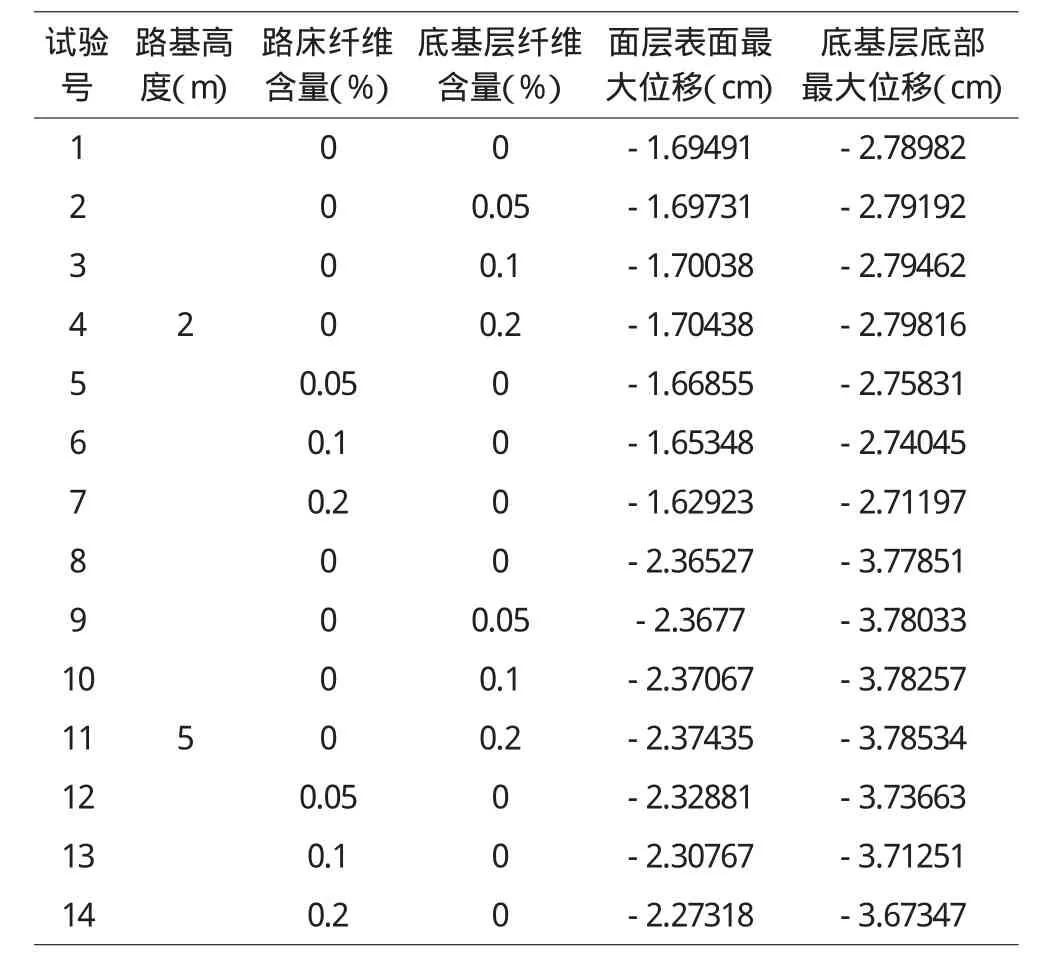
结构层最大位移 表4

进行数值计算得路面加载后，道路表面、基层底部和底基层底部的水平应力沿x方向变化曲线如图9～11所示。

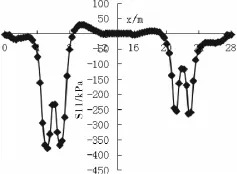
图9 面层表面水平应力沿x方向分布

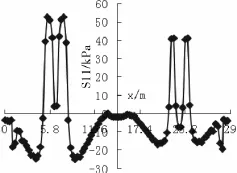
图10 路面基层底部水平应力沿x方向分布

图11 底基层底部水平应力沿x方向分布

在不同路床、底基层材料和不同路基高度下，进行计算得到道路表面和底基层底部的最大水平应力见表5，其中负数表示压应力，正数表示拉应力。

结构层最大水平应力 表5

根据表4数据得到：

①路床未掺加纤维，而底基层掺加纤维时，纤维的掺加对道路表面和底基层底部的最大位移影响很小。

道路结构层最大位移与路床纤维含量关系方程式 表6

道路结构层最大水平应力与路床纤维含量关系方程式 表8

②底基层未掺加纤维，而路床掺加纤维时，随路床纤维含量的增加，道路表面和底基层底部的最大位移均逐渐减小。对道路结构层最大位移与路床纤维含量关系进行曲线拟合得。

由表6中公式可以算得，在相同的路床纤维配比下，路基高度为2m的道路表面的最大位移是5m高路基的0.72倍左右，底基层底部的最大位移是5m高路基的0.74倍左右。

根据表5数据得：

①路床未掺加纤维，而底基层掺加纤维时，纤维的掺加对道路表面最大压应力的影响很小。

②随底基层纤维含量的增加，底基层底部的最大水平拉应力逐渐减小，但随路基高度的增加，纤维含量的变化对应力的影响逐渐减小。对这些关系用二次方程进行拟合得到表7。

道路结构层最大水平应力与底基层纤维含量关系方程式 表7

根据公式5可以算出，在路基高度为2m的情况下，当底基层纤维含量小于0.29%时，随纤维含量的增加，底基层底部的最大水平应力逐渐减小，当超过0.29%时，应力不再减小，所以取0.29%为纤维的最佳掺配比例，此时，与未掺加纤维相比，底基层底部的最大水平应力降低了22.6%。

根据公式6算得，当路基高度为5m时，底基层纤维的最佳掺配比例为0.26%，与未掺加纤维相比，底基层底部的最大水平应力降低了10%。

③当底基层未掺加纤维，而路床掺加纤维时，随路床纤维含量的增加，道路表面的最大水平压应力逐渐减小，底基层底部的最大水平拉应力也逐渐减小。但随路基高度的增加，纤维含量的变化对水平应力的影响逐渐减小。对这些关系曲线进行二次拟合得到表8。

根据公式8算得，当路基高度为2m时，路床纤维的最佳掺配比例为0.25%，与未掺加纤维相比，底基层底部的最大水平应力降低了15.7%。

根据公式10算得，当路基高度为5m时，路床层纤维的最佳掺配比例为0.23%，与未掺加纤维相比，底基层底部的最大水平应力降低了20.9%。

①当路基高度为2m时，应优先考虑对底基层进行改善，底基层纤维的最佳配合比为0.29%。

②当路基高度为5m时，应优先考虑对路床进行改善，路床纤维的最佳配合比为0.23%。

③实际工程使用时，还需根据现场的施工工艺和试验检测数据，对纤维土的配合比酌情增减。

[1]熊有言.土工合成纤维土[J].中国公路学报，1990,3(4)：84-88.

[2]黄文生.纤维土——一种新的加固材料 [J].国外公路，1990(3)：48-51.

[3]陈晔,张起森.纤维加固土路面基层的研究与应用[M].北京：人民交通出版社，1995.

[4]张艳美,张旭东,张鸿儒.土工合成纤维土补强机理试验研究及工程应用[J].岩土力学，2005(8)：1323-1326.

[5]赵莹莹，赵燕茹，李驰，韩金宝.纤维土的三轴试验研究[J].水利与建筑工程学报，2009，7(1)：127-128.

[6]沈圆顺,刘玖壮,郭丽丽.纤维土作为录用材料的试验研究[J].建筑材料学报，2010，13(4)：545-549.

TU441+.4

A

1007-7359（2016）05-0189-04

10.16330/j.cnki.1007-7359.2016.05.066

宫剑（1969-），男，安徽淮南人，本科，工程师，主要从事淮南地区建筑监督管理方面的工作。